18.1.2 平行四边形的判定(3)三角形的中位线定理课件 共20张PPT
文档属性
| 名称 | 18.1.2 平行四边形的判定(3)三角形的中位线定理课件 共20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-23 09:56:02 | ||
图片预览





文档简介
课件20张PPT。平行四边形的判定三
1. 理解三角形中位线的概念,掌握它的性质.
2. 能较熟练地应用三角形中位线性质进行有
关的证明和计算.
3.经历探索、猜想、证明的过程,进一步发展
推理论证的能力
学习目标
.重点:掌握和运用三角形中位线的性质.难点:三角形中位线性质的证明(辅助线
的添加方法). 学科网温故知新 平行四边形的判定边角对角线两组对边分别平行的四边形是平行四边形一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形探究思考 请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.学科网探究思考 问题1:
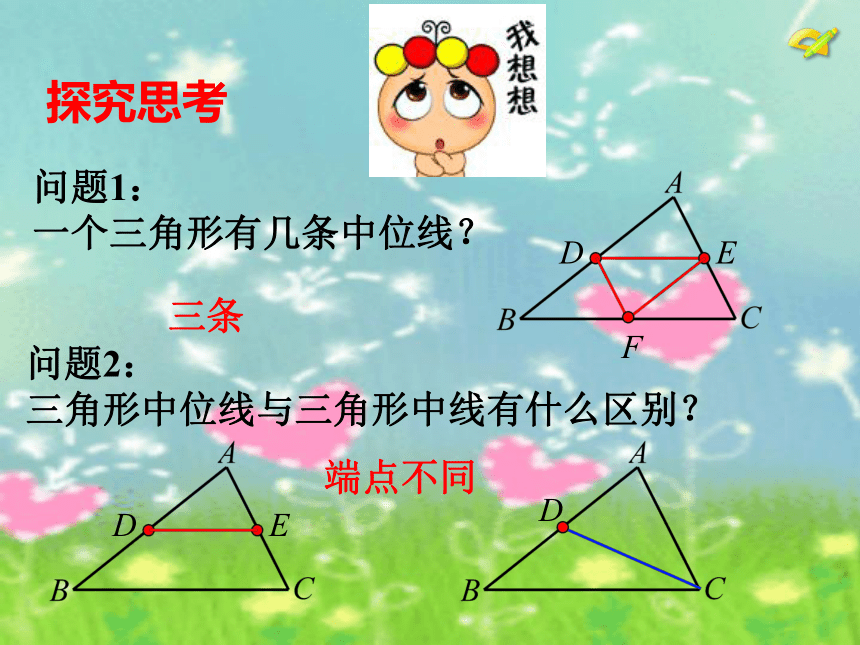
一个三角形有几条中位线?F三条问题2:
三角形中位线与三角形中线有什么区别?D端点不同探究思考 问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?两条线段的关系位置关系数量关系分析:DE与BC的关系猜想:DE∥BC? 度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.问题4:探究思考
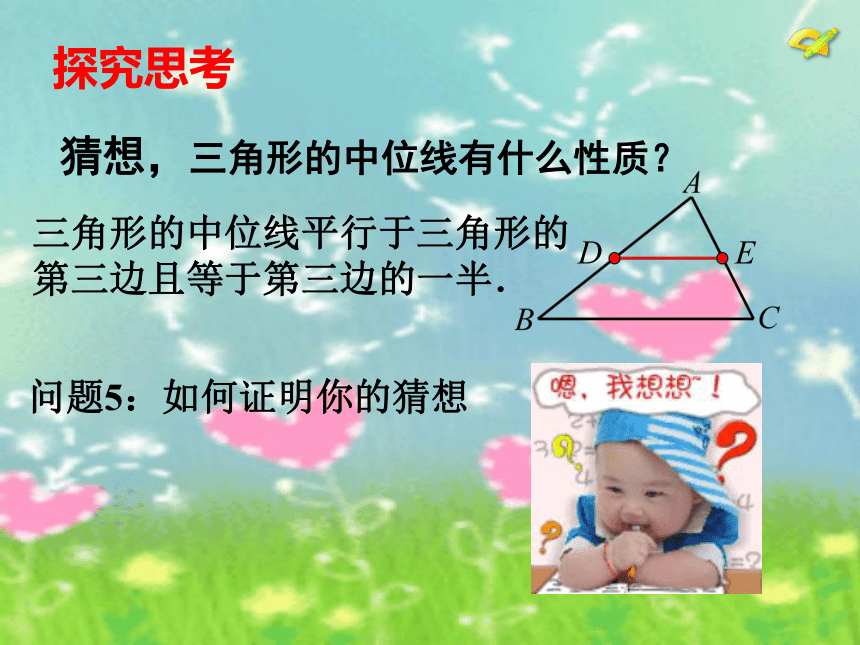
三角形的中位线平行于三角形的
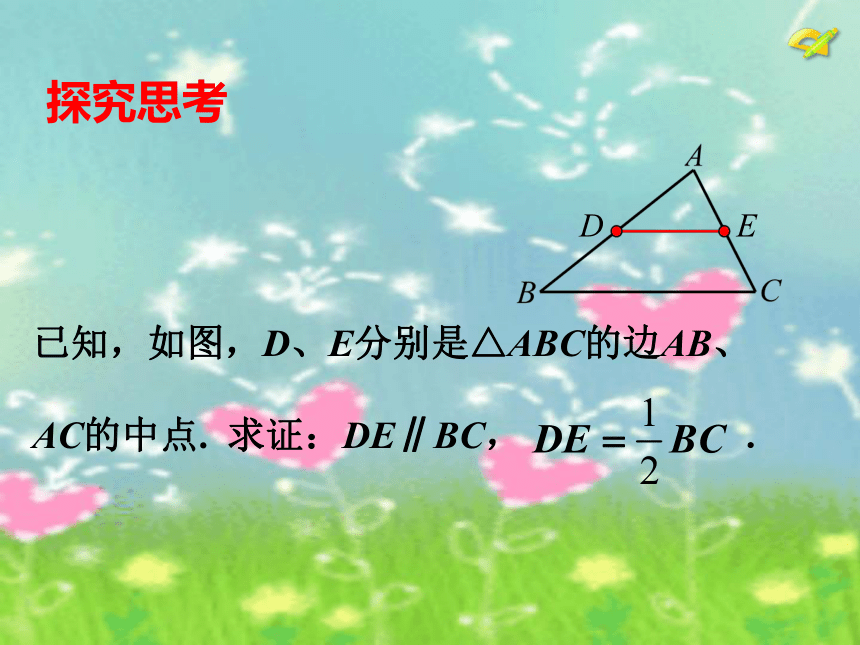
第三边且等于第三边的一半. 问题5:如何证明你的猜想猜想,三角形的中位线有什么性质?探究思考 已知,如图,D、E分别是△ABC的边AB、
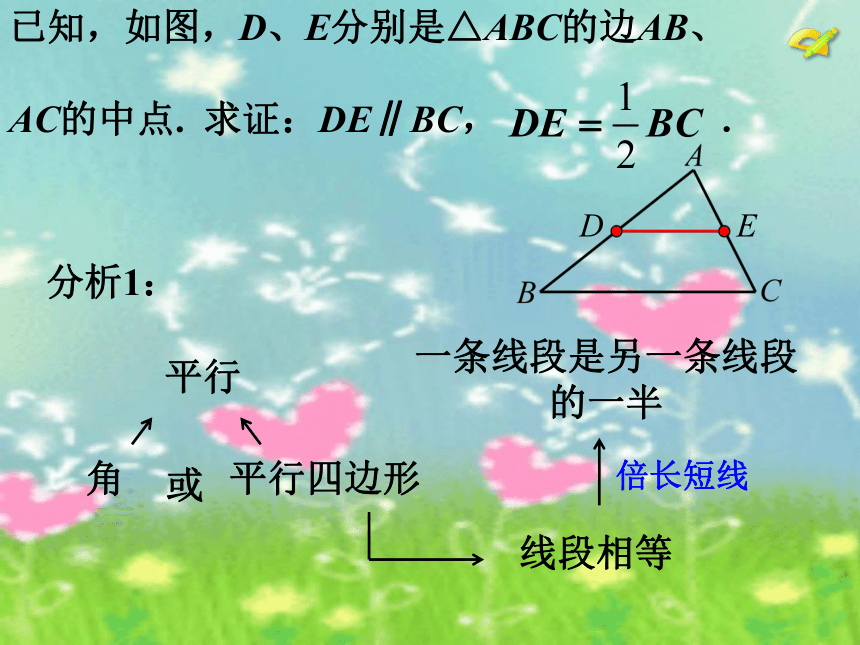
AC的中点. 求证:DE∥BC, . 平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析1:已知,如图,D、E分别是△ABC的边AB、
AC的中点. 求证:DE∥BC, .探究思考 证明:延长DE到F,使EF=DE.F∴四边形BCFD是平行四边形.∴△ADE≌△CFE.∴∠ADE=∠F连接FC.∵∠AED=∠CEF,AE=CE,证法1: ,AD CF.∴BD CF.探究思考 证明:∴ DE∥BC, .F又 ,∴DF BC .探究思考 证明:延长DE到F,使EF=DE.连接AF、CF、DC .∵AE=EC,DE=EF ,∴四边形ADCF是平行四边形.F∴四边形BCFD是平行四边形.证法2:∴CF AD .∴CF BD .(下面证明同证法1)探究思考 三角形的中位线平行于三角形的
第三边且等于第三边的一半.△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.三角形中位线定理:符号语言: (1)证明平行
(2)证明一条线段是另一条线
段的2倍或ABCDE 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线定理的主要用途:
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4D 8cm6cm 平行于
等于 一半 学以致用学以致用 4. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么? 分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
NM根据是三角形中位线定理.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。挑战自我三角形中位线定义三角形中位线定理三角形中位线定理应用本节课你有哪些收获?思想方法方面:转化思想课本P50习题18.1第5题,第11题,12题,13题。今日作业:5、如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。6、在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811
1. 理解三角形中位线的概念,掌握它的性质.
2. 能较熟练地应用三角形中位线性质进行有
关的证明和计算.
3.经历探索、猜想、证明的过程,进一步发展
推理论证的能力
学习目标
.重点:掌握和运用三角形中位线的性质.难点:三角形中位线性质的证明(辅助线
的添加方法). 学科网温故知新 平行四边形的判定边角对角线两组对边分别平行的四边形是平行四边形一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形探究思考 请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.学科网探究思考 问题1:
一个三角形有几条中位线?F三条问题2:
三角形中位线与三角形中线有什么区别?D端点不同探究思考 问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?两条线段的关系位置关系数量关系分析:DE与BC的关系猜想:DE∥BC? 度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.问题4:探究思考
三角形的中位线平行于三角形的
第三边且等于第三边的一半. 问题5:如何证明你的猜想猜想,三角形的中位线有什么性质?探究思考 已知,如图,D、E分别是△ABC的边AB、
AC的中点. 求证:DE∥BC, . 平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析1:已知,如图,D、E分别是△ABC的边AB、
AC的中点. 求证:DE∥BC, .探究思考 证明:延长DE到F,使EF=DE.F∴四边形BCFD是平行四边形.∴△ADE≌△CFE.∴∠ADE=∠F连接FC.∵∠AED=∠CEF,AE=CE,证法1: ,AD CF.∴BD CF.探究思考 证明:∴ DE∥BC, .F又 ,∴DF BC .探究思考 证明:延长DE到F,使EF=DE.连接AF、CF、DC .∵AE=EC,DE=EF ,∴四边形ADCF是平行四边形.F∴四边形BCFD是平行四边形.证法2:∴CF AD .∴CF BD .(下面证明同证法1)探究思考 三角形的中位线平行于三角形的
第三边且等于第三边的一半.△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.三角形中位线定理:符号语言: (1)证明平行
(2)证明一条线段是另一条线
段的2倍或ABCDE 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线定理的主要用途:
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4D 8cm6cm 平行于
等于 一半 学以致用学以致用 4. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么? 分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
NM根据是三角形中位线定理.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。挑战自我三角形中位线定义三角形中位线定理三角形中位线定理应用本节课你有哪些收获?思想方法方面:转化思想课本P50习题18.1第5题,第11题,12题,13题。今日作业:5、如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。6、在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811
