六年级下册数学课件-1.数与代数 第4课时 数的运算(2)(人教版)(共21张PPT)
文档属性
| 名称 | 六年级下册数学课件-1.数与代数 第4课时 数的运算(2)(人教版)(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-19 00:00:00 | ||
图片预览








文档简介
课件21张PPT。1. 数与代数第4课时 数的运算(2)
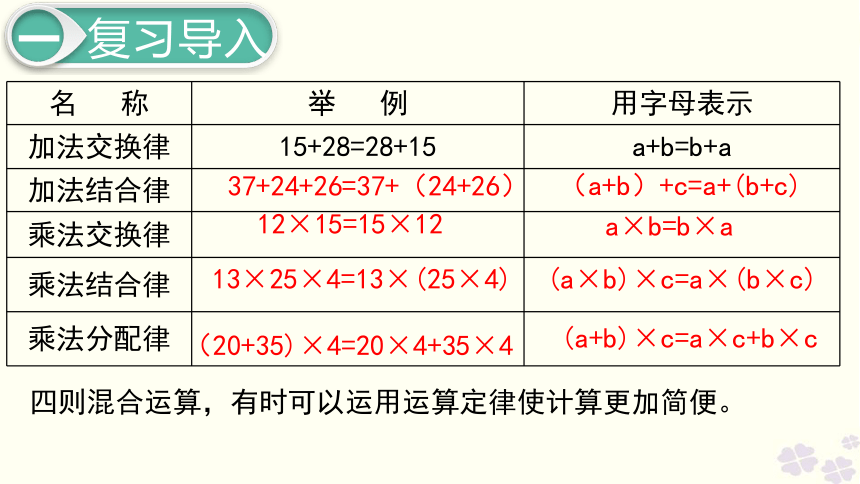
(a+b)+c=a+(b+c)a×b=b×a(a×b)×c=a×(b×c)(a+b)×c=a×c+b×c四则混合运算,有时可以运用运算定律使计算更加简便。37+24+26=37+(24+26)12×15=15×1213×25×4=13×(25×4)(20+35)×4=20×4+35×4简便运算把简算的式题进行分类,怎么分?(1)加上或减去接近整数、整十数的运算 3.87+2.99=3.87+3-0.01 像这类题目简算的时候一般先加上或减去整数,多加了几就减几,多减了几就加几。 75.2-19.8=75.2-20+0.2(2)根据加法交换率和结合律,使运算简便 a + b = b + a
(a + b)+ c = a +(b + c)(3)根据减法性质,使运算简便 a- b- c = a-(b + c)
a- b- c = a -c -b 10.47-5.68-1.325.39-2.88-1.39(4)根据乘法的交换律、结合律、分配律使运算简便。a×b=b×a
a×b×c=a×(b×c)
(a+b)×c=a×c+b×c1.25×7238×56+44×3894×101 1.25×72=1.25×8×9
(算式中有125应想到8,因为125×8=1000,乘积得整百整千的数,算起来方便。)
38×56+44×38=38×(56+44)
(两个不同的因数相加组成整十、整百、整千的数,这样计算起来简便。)
94×101=94×(100+1)=94×100+94×1
(一个因数接近整十、整百,拆成和或差的形式。)(5)除法的运算性质a÷(b×c)=a÷b÷c a÷(b÷c)=a÷b×c3900÷(39×25) 5700÷(57÷9) 例 六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交1/4。两个班共交了多少件作品?(1)解决问题时一般可以分成几个主要步骤?每一步做
什么?
(2)分析数量关系时有几种方法?你运用的是什么方法?
(3)需要借助线段图等直观手段吗?
(4)解决问题时要注意什么?思考首先:理解题意,找出已知信息和所求问题;
其次:分析数量关系,确定先算什么,再算什么,
最后算什么;
再次:确定每一步该怎样算,列出算式,算出得数;
最后:进行检验,写出答案。(检验是解决问
题的一个步骤,要养成检验的好习惯。)解决问题的一般步骤是: 六年级矩形“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交1/4。两个班共交了多少件作品?10画线段图分析①六(2)班作品是六(1)班的几分之几?
画线段图分析②求六(2)班交了多少件作品,实际是求什么?
解决问题常用的分析方法:(1)综合法:从已知信息入手,利用已知信息看能解决什么问题,直到求出未知数。(2)分析法:从所求的问题出发,逐步找出解答问题所需要的条件,依次推导,直到问题解决。 在解决实际问题时,为了方便我们分析题意,还应该记住一些常用的数量关系。你能说出哪些常见的数量关系?单产量、数量、总产量
单产量×数量=总产量本金、时间、利率、利息
本金×利率×时间=利息收入、支出、结余
收入-支出=结余单价、数量、总价
单价×数量=总价速度、时间、路程
速度×时间=路程工作效率、时间、工作总量
工作效率×时间=工作总量2.计算 3.举例说明估算的应用,你知道哪些估算策略?
(1)7.99×9.99与80比,哪个大?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6
元;又花39.6元买了一本汉语词典;之后,妈妈还想买
一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,
厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪
一本?80大比1大20.6+20.6+39.6≈80(元)100-80=20(元)
20元>13.7元 答:这时她的钱够买薄本的。(2)
(a+b)+c=a+(b+c)a×b=b×a(a×b)×c=a×(b×c)(a+b)×c=a×c+b×c四则混合运算,有时可以运用运算定律使计算更加简便。37+24+26=37+(24+26)12×15=15×1213×25×4=13×(25×4)(20+35)×4=20×4+35×4简便运算把简算的式题进行分类,怎么分?(1)加上或减去接近整数、整十数的运算 3.87+2.99=3.87+3-0.01 像这类题目简算的时候一般先加上或减去整数,多加了几就减几,多减了几就加几。 75.2-19.8=75.2-20+0.2(2)根据加法交换率和结合律,使运算简便 a + b = b + a
(a + b)+ c = a +(b + c)(3)根据减法性质,使运算简便 a- b- c = a-(b + c)
a- b- c = a -c -b 10.47-5.68-1.325.39-2.88-1.39(4)根据乘法的交换律、结合律、分配律使运算简便。a×b=b×a
a×b×c=a×(b×c)
(a+b)×c=a×c+b×c1.25×7238×56+44×3894×101 1.25×72=1.25×8×9
(算式中有125应想到8,因为125×8=1000,乘积得整百整千的数,算起来方便。)
38×56+44×38=38×(56+44)
(两个不同的因数相加组成整十、整百、整千的数,这样计算起来简便。)
94×101=94×(100+1)=94×100+94×1
(一个因数接近整十、整百,拆成和或差的形式。)(5)除法的运算性质a÷(b×c)=a÷b÷c a÷(b÷c)=a÷b×c3900÷(39×25) 5700÷(57÷9) 例 六年级举行“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交1/4。两个班共交了多少件作品?(1)解决问题时一般可以分成几个主要步骤?每一步做
什么?
(2)分析数量关系时有几种方法?你运用的是什么方法?
(3)需要借助线段图等直观手段吗?
(4)解决问题时要注意什么?思考首先:理解题意,找出已知信息和所求问题;
其次:分析数量关系,确定先算什么,再算什么,
最后算什么;
再次:确定每一步该怎样算,列出算式,算出得数;
最后:进行检验,写出答案。(检验是解决问
题的一个步骤,要养成检验的好习惯。)解决问题的一般步骤是: 六年级矩形“小发明”比赛,六(1)班同学上交32件作品,六(2)班比六(1)班多交1/4。两个班共交了多少件作品?10画线段图分析①六(2)班作品是六(1)班的几分之几?
画线段图分析②求六(2)班交了多少件作品,实际是求什么?
解决问题常用的分析方法:(1)综合法:从已知信息入手,利用已知信息看能解决什么问题,直到求出未知数。(2)分析法:从所求的问题出发,逐步找出解答问题所需要的条件,依次推导,直到问题解决。 在解决实际问题时,为了方便我们分析题意,还应该记住一些常用的数量关系。你能说出哪些常见的数量关系?单产量、数量、总产量
单产量×数量=总产量本金、时间、利率、利息
本金×利率×时间=利息收入、支出、结余
收入-支出=结余单价、数量、总价
单价×数量=总价速度、时间、路程
速度×时间=路程工作效率、时间、工作总量
工作效率×时间=工作总量2.计算 3.举例说明估算的应用,你知道哪些估算策略?
(1)7.99×9.99与80比,哪个大?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6
元;又花39.6元买了一本汉语词典;之后,妈妈还想买
一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,
厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪
一本?80大比1大20.6+20.6+39.6≈80(元)100-80=20(元)
20元>13.7元 答:这时她的钱够买薄本的。(2)
