2018-2019学年广东省汕头市龙湖实验中学九年级(下)开学数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年广东省汕头市龙湖实验中学九年级(下)开学数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-19 14:30:50 | ||
图片预览


文档简介
2018-2019学年广东省汕头市龙湖实验中学九年级(下)开学数学试卷
一、选择题(共10小题,每小题3分,满分30分)
1.下列图案中花边的内外边缘(每个图形边缘等宽)所围成的图形不相似的是( )
A. B. C. D.
2.下列方程中,关于x的一元二次方程是( )
A.(x﹣1)(x﹣2)=2 B. +=2
C.ax2+bx+c=0 D.3x2﹣2y=0
3.用配方法解一元二次方程x2+4x+3=0,下列配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=7 D.(x﹣2)2=7
4.下列关于反比例函数y=的说法正确的是( )
A.y随x的增大而增大
B.函数图象过点(2,)
C.图象位于第一、第三象限
D.x>0时,y随x的增大而增大
5.关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
A.q<16 B.q>16 C.q≤4 D.q≥4
6.半径为6,圆心角为120°的扇形的面积是( )
A.3π B.6π C.9π D.12π
7.线段a、b、c、d是成比例线段,a=4、b=2、c=2,则d的长为( )
A.1 B.2 C.3 D.4
8.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB1C1,若AC=2,则图中阴影部分的面积为( )
A. B. C. D.
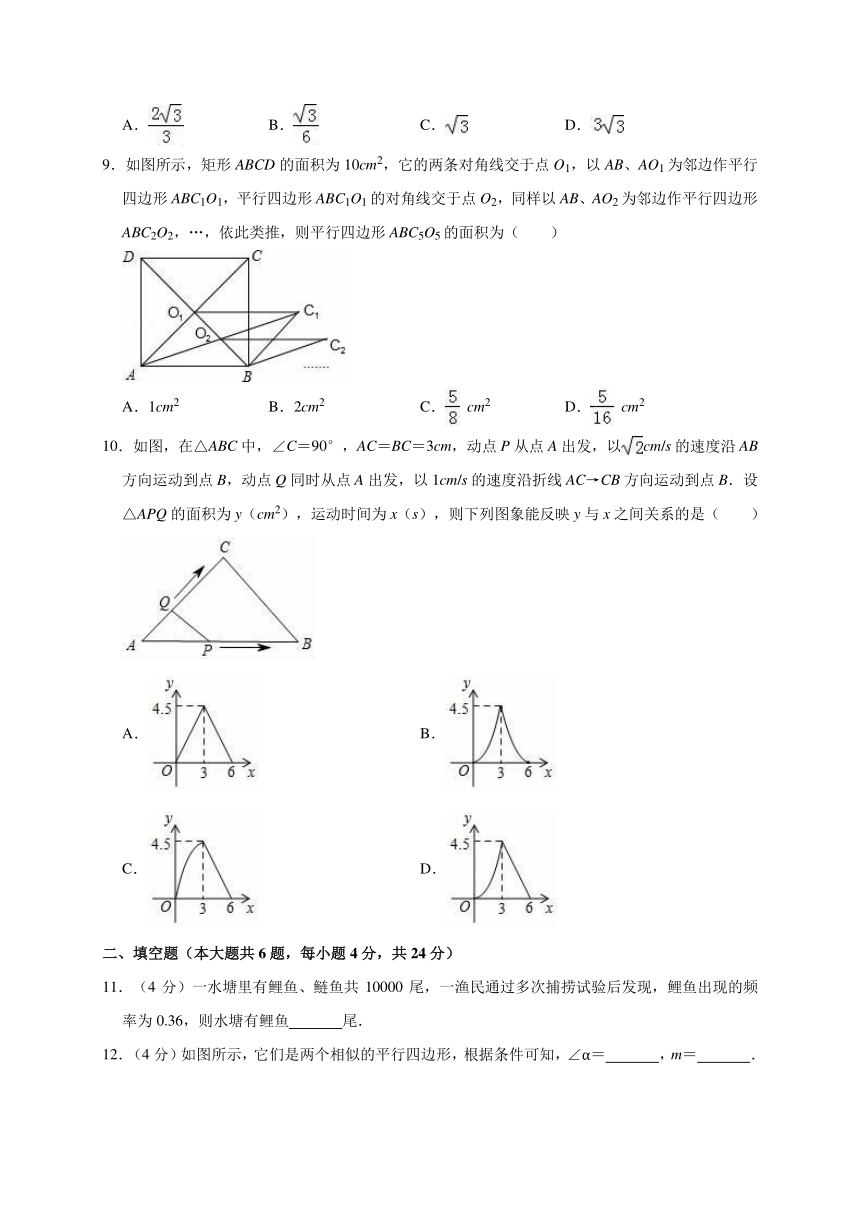
9.如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC5O5的面积为( )
A.1cm2 B.2cm2 C. cm2 D. cm2
10.如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
二、填空题(本大题共6题,每小题4分,共24分)
11.(4分)一水塘里有鲤鱼、鲢鱼共10000尾,一渔民通过多次捕捞试验后发现,鲤鱼出现的频率为0.36,则水塘有鲤鱼 尾.
12.(4分)如图所示,它们是两个相似的平行四边形,根据条件可知,∠α= ,m= .
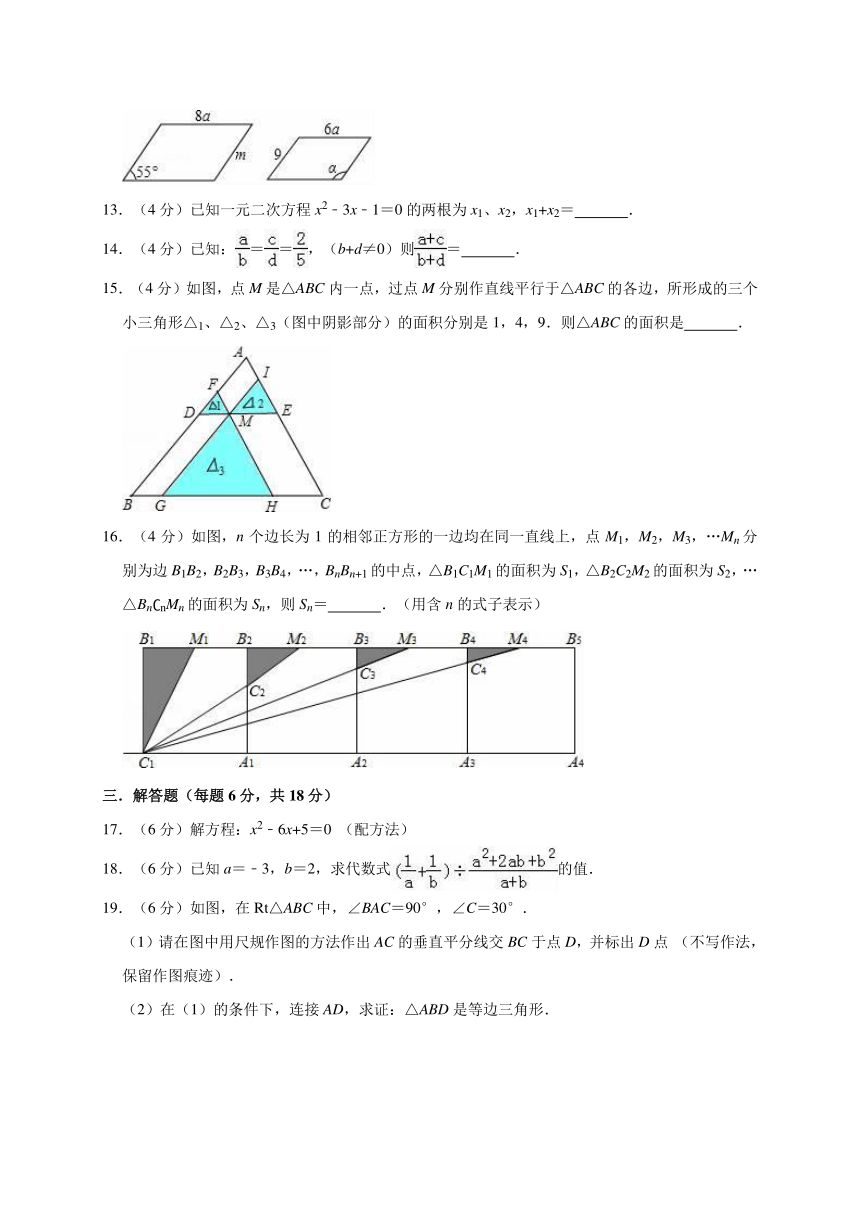
13.(4分)已知一元二次方程x2﹣3x﹣1=0的两根为x1、x2,x1+x2= .
14.(4分)已知:==,(b+d≠0)则= .
15.(4分)如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,4,9.则△ABC的面积是 .
16.(4分)如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△Bn?nMn的面积为Sn,则Sn= .(用含n的式子表示)
三.解答题(每题6分,共18分)
17.(6分)解方程:x2﹣6x+5=0 (配方法)
18.(6分)已知a=﹣3,b=2,求代数式的值.
19.(6分)如图,在Rt△ABC中,∠BAC=90°,∠C=30°.
(1)请在图中用尺规作图的方法作出AC的垂直平分线交BC于点D,并标出D点 (不写作法,保留作图痕迹).
(2)在(1)的条件下,连接AD,求证:△ABD是等边三角形.
四、解答题(每题7分,共21分)
20.(7分)有四张正面分别标有数字﹣2,﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们正面朝下,洗匀后从中抽出一张记下数字,放回洗匀后再从中抽出一张记下数字.
(1)请用列表或画树状图的方法表示两次抽出卡片上的数字的所有结果;
(2)若将第一次抽出的数字作为点的横坐标a,第二次抽出的数字作为点的纵坐标b,求点(a,b)落在双曲线上的概率.
21.(7分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
22.(7分)某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
五.解答题(本大题共3题,每题9分,共27分)
23.(9分)如图,一次函数y=kx+2的图象与反比例函数y=的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,=.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
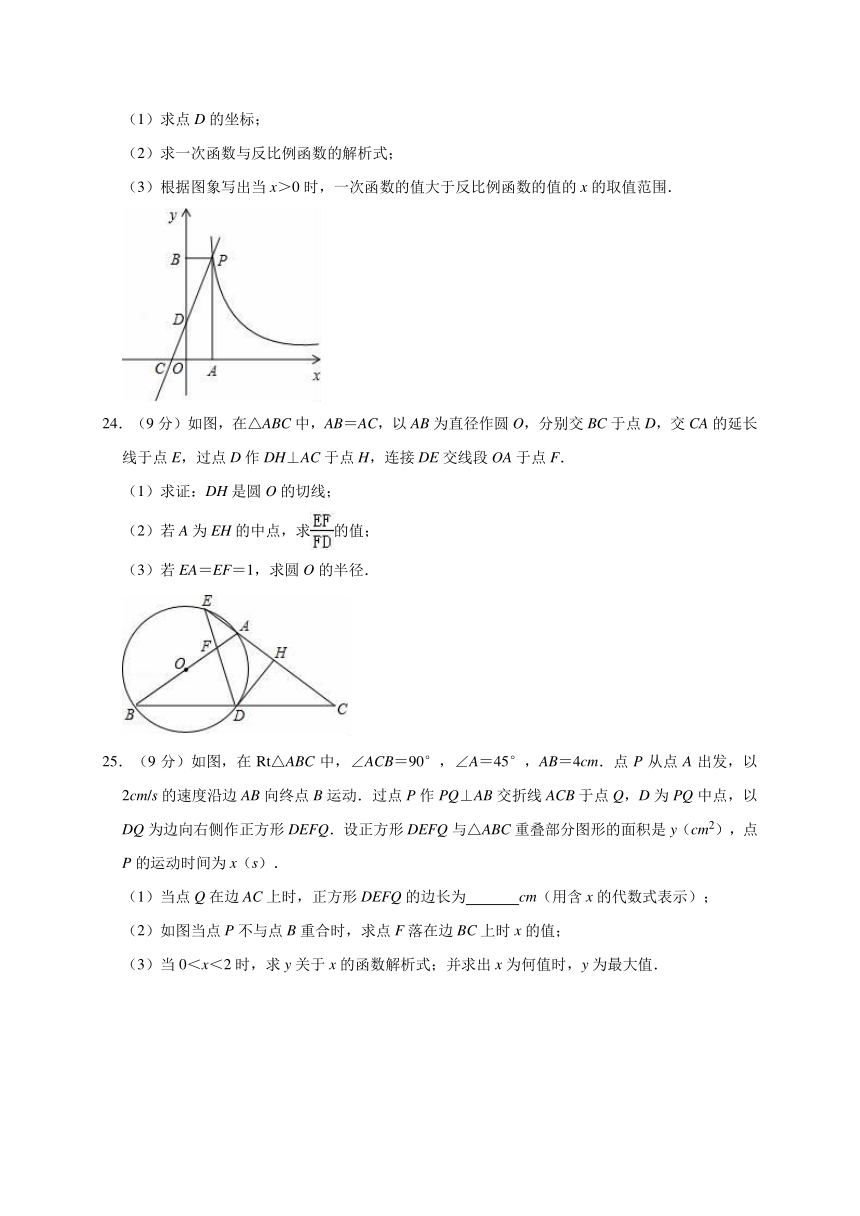
24.(9分)如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求的值;
(3)若EA=EF=1,求圆O的半径.
25.(9分)如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)如图当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;并求出x为何值时,y为最大值.
2018-2019学年广东省汕头市龙湖实验中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(共10小题,每小题3分,满分30分)
1.【分析】根据相似图形的定义,结合图形,对选项一一分析,排除不符合要求答案.
【解答】解:A、两个不等边三角形形状相同,符合相似形的定义,故A选项不符合要求;
B、两个等边三角形形状相同,符合相似形的定义,故B选项不符合要求;
C、两个正方形形状相同,符合相似形的定义,故C选项不符合要求;
D、两个矩形,虽然四个角对应相等,但对应边不成比例,故D选项符合要求;
故选:D.
【点评】本题考查的是相似形的定义,联系图形,即形状相同,大小不一定相同的图形叫做相似形.
2.【分析】根据一元二次方程的定义:未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数,可得答案.
【解答】解:A、由原方程知:x2﹣3x+1=0,符合一元二次方程的定义,故本选项正确;
B、该方程是分式方程,故本选项错误;
C、当a=0时,该方程不是一元二次方程,故本选项错误;
D、该方程中含有两个未知数,是二元二次方程,故本选项错误;
故选:A.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
3.【分析】方程移项后,两边加上4变形即可得到结果.
【解答】解:方程移项得:x2+4x=﹣3,
配方得:x2+4x+4=1,即(x+2)2=1.
故选:A.
【点评】此题考查了解一元二次方程﹣配方法,熟练掌握完全平方公式是解本题的关键.
4.【分析】直接利用反比例函数的性质分别分析得出答案.
【解答】解:A、反比例函数y=,每个象限内,y随x的增大而增大,故此选项错误;
B、函数图象过点(2,﹣),故此选项错误;
C、函数图象图象位于第二、第四象限,故此选项错误;
D、x>0时,y随x的增大而增大,正确.
故选:D.
【点评】此题主要考查了反比例函数的性质,正确记忆相关性质是解题关键.
5.【分析】根据方程的系数结合根的判别式,即可得出△=64﹣4q>0,解之即可得出q的取值范围.
【解答】解:∵关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,
∴△=82﹣4q=64﹣4q>0,
解得:q<16.
故选:A.
【点评】本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键.
6.【分析】根据扇形的面积公式S=计算即可.
【解答】解:S==12π,
故选:D.
【点评】本题考查的是扇形面积的计算,掌握扇形的面积公式S=是解题的关键.
7.【分析】根据成比例线段的概念,得a:b=c:d,再根据比例的基本性质,可求得d的值.
【解答】解:∵a、b、c、d是成比例线段,
∴a:b=c:d,
即4:2=2:d,
∴d=1;
故选:A.
【点评】此题考查了比例线段,用到的知识点是比例线段的概念,在写的时候,注意按照字母的顺序.
8.【分析】根据题意,阴影部分为含30°锐角的直角三角形.已知长直角边可求短直角边长,再代入面积公式计算求解.
【解答】解:∵等腰直角△ABC绕点A逆时针旋转15°后得到△AB′C′,
∵∠CAC′=15°,
∴∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=2,
∴阴影部分的面积=×2×tan30°×2=,
故选:A.
【点评】此题考查旋转的性质及解直角三角形,掌握旋转的性质及三角函数的定义是解题的关键.
9.【分析】根据矩形的性质对角线互相平分可知O1是AC与DB的中点,根据等底同高得到S△ABO1=S矩形,又ABC1O1为平行四边形,根据平行四边形的性质对角线互相平分,得到O1O2=BO2,所以S△ABO2=S矩形,…,以此类推得到S△ABO5=S矩形,而S△ABO5等于平行四边形ABC5O5的面积的一半,根据矩形的面积即可求出平行四边形ABC5O5的面积.
【解答】解:∵设平行四边形ABC1O1的面积为S1,∴S△ABO1=S1,
又S△ABO1=S矩形,∴S1=S矩形=5=;
设ABC2O2为平行四边形为S2,∴S△ABO2=S2,
又S△ABO2=S矩形,∴S2=S矩形==;
,…,
同理:设ABC5O5为平行四边形为S5,S5==.
故选:D.
【点评】此题综合考查了矩形及平行四边形的性质,要求学生审清题意,找出面积之间的关系,归纳总结出一般性的结论.考查了学生观察、猜想、验证及归纳总结的能力.
10.【分析】作QD⊥AB,分点Q在AC、CB上运动这两种情况,由直角三角形的性质表示出QD的长,利用三角形面积公式得出函数解析式即可判断.
【解答】解:(1)过点Q作QD⊥AB于点D,
①如图1,当点Q在AC上运动时,即0≤x≤3,
由题意知AQ=x、AP=x,
∵∠A=45°,
∴QD=AQ=x,
则y=?x?x=x2;
②如图2,当点Q在CB上运动时,即3<x≤6,此时点P与点B重合,
由题意知BQ=6﹣x、AP=AB=3,
∵∠B=45°,
∴QD=BQ=(6﹣x),
则y=×3×(6﹣x)=﹣x+9;
故选:D.
【点评】本题主要考查动点问题的函数图象,解题的关键是根据题意弄清两点的运动路线,据此分类讨论并得出函数解析式.
二、填空题(本大题共6题,每小题4分,共24分)
11.【分析】由于水塘里有鲤鱼、鲢鱼共10000尾,而鲤鱼出现的频率为0.36,然后乘以总数即可得到水塘有鲤鱼有多少尾.
【解答】解:水塘约有鲤鱼10000×0.36=3600(尾),
故答案为:3600.
【点评】此题主要考查了利用频率估计概率的思想,首先通过实验得到事件的频率,然后即可估计事件的概率.
12.【分析】根据平行四边形的性质得到AB∥CD,AB=CD=m,根据相似多边形的性质列式计算,得到答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=m,
∴∠C=180°﹣55°=125°,
∵两个平行四边形相似,
∴α=∠C=125°,=,
解得,m=12,
故答案为:125°;12.
【点评】本题考查的是相似多边形的性质、平行四边形的性质,掌握相似多边形的对应角相等、对应边的比相等是解题的关键.
13.【分析】根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=﹣,代入计算即可.
【解答】解:∵一元二次方程x2﹣3x﹣1=0的两根是x1、x2,
∴x1+x2=3,
故答案为:3.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=﹣,x1?x2=.
14.【分析】分别设a为2m,c=2n,进而得到用m,n表示的b,d的值,把它们代入所给代数式求解即可.
【解答】解:设a为2m,c=2n,则b=5m,d=5n.
∴===,
故答案为.
【点评】考查等比性质的应用:若==k,则=k.
15.【分析】根据相似三角形的面积比是相似比的平方,先求出相似比.再根据平行四边形的性质及相似三角形的性质得到BC:DM=6:1,即S△ABC:S△FDM=36:1,从而得到△ABC面积.
【解答】解:过M作BC的平行线交AB、AC于D、E,
过M作AC的平行线交AB、BC于F、H,
过M作AB的平行线交AC、BC于I、G,
因为△1、△2、△3的面积比为1:4:9,
所以他们对应边边长的比为1:2:3,
又因为四边形BDMG与四边形CEMH为平行四边形,
所以DM=BG,EM=CH,
设DM为x,则ME=2x,GH=3x,
所以BC=BG+GH+CH=DM+GH+ME=x+2x+3x=6x,
所以BC:DM=6x:x=6:1,
由面积比等于相似比的平方故可得出:S△ABC:S△FDM=36:1,
所以S△ABC=36×S△FDM=36×1=36.
故答案为:36.
【点评】本题考查了平行线的性质,平行四边形的性质及相似三角形的性质.熟悉相似三角形的性质:相似三角形的面积比是相似比的平方.
16.【分析】利用相似三角形的性质求出Bn?n,再利用三角形的面积公式计算即可;
【解答】解:∵Bn?n∥B1C1,
∴△MnBn?n∽△MmB1C1,
∴=,
∴=,
∴Bn?n=,
∴Sn=××=,
故答案为.
【点评】本题考查相似三角形的判定和性质、正方形的性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
三.解答题(每题6分,共18分)
17.【分析】利用配方法解方程.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
【解答】解:由原方程移项,得
x2﹣6x=﹣5,
等式两边同时加上一次项系数一半的平方32.得
x2﹣6x+32=﹣5+32,即(x﹣3)2=4,
∴x=3±2,
∴原方程的解是:x1=5,x2=1.
【点评】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
18.【分析】将所求式子括号中的两项通分并利用同分母分式的减法法则计算,后一项分子利用完全平方式分解因式后约分,得到最简结果,然后将a与b的值代入化简后的式子中计算,即可得到所求式子的值.
【解答】解:
=÷
=÷(a+b)
=,
当a=﹣3,b=2时,
原式==﹣.
【点评】此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应先将多项式分解因式后再约分.
19.【分析】(1)作线段AC的垂直平分线即可;
(2)根据线段垂直平分线的性质可得DA=DC,根据等边对等角可得∠CAD=∠C,进而可得∠ADB=∠B=∠DAB=60°,然后可得答案.
【解答】解:(1)如图所示:
(2)∵∠BAC=90°,∠C=30°
∴∠B=60°,
又∵点D在AC的垂直平分线上,
∴DA=DC,
∴∠CAD=∠C=30°,
∴∠DAB=60°,
∴∠ADB=∠B=∠DAB=60°,
即△ABD是等边三角形.
【点评】此题主要考查了基本作图,以及线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
四、解答题(每题7分,共21分)
20.【分析】(1)列表得出所有等可能的情况数即可;
(2)找出在双曲线y=上的点的情况数,即可求出所求的概率.
【解答】解:(1)列表如下:
﹣2 ﹣1 1 2
﹣2 ﹣2,﹣2 ﹣2,﹣1 ﹣2,1 ﹣2,2
﹣1 ﹣1,﹣2 ﹣1,﹣1 ﹣1,1 ﹣1,2
1 1,﹣2 1,﹣1 1,1 1,2
2 2,﹣2 2,﹣1 2,1 2,2
由上表可知,两次抽出卡片上的数字的所有结果一共有16种;
(2)∵上述16种结果出现的可能性相同,且在双曲线y=上的点有四个,它们分别是(﹣2,﹣1),(﹣1,﹣2),(1,2),(2,1),
∴点(a,b)落在双曲线y=上的概率P==.
【点评】此题考查了列表法与树状图法,以及反比例函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.
21.【分析】(1)首先证明AB=AF=AD,然后再证明∠AFG=90°,接下来,依据HL可证明△ABG≌△AFG;
(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可.
【解答】解:(1)在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
,
∴△ABG≌△AFG(HL);
(2)∵△ABG≌△AFG,
∴BG=FG,
设BG=FG=x,则GC=6﹣x,
∵E为CD的中点,
∴CE=EF=DE=3,
∴EG=3+x,
∴在Rt△CEG中,32+(6﹣x)2=(3+x)2,解得x=2,
∴BG=2.
【点评】此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.
22.【分析】(1)首先设A种型号计算器的销售价格是x元,A种型号计算器的销售价格是y元,根据题意可等量关系:①5台A型号和1台B型号计算器,可获利润76元;②销售6台A型号和3台B型号计算器,可获利润120元,根据等量关系列出方程组,再解即可;
(2)根据题意表示出所用成本,进而得出不等式求出即可.
【解答】解:(1)设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y元,由题意得:
,
解得:;
答:A种型号计算器的销售价格是42元,B种型号计算器的销售价格是56元;
(2)设购进A型计算器a台,则购进B型计算器:(70﹣a)台,
则30a+40(70﹣a)≤2500,
解得:a≥30,
答:最少需要购进A型号的计算器30台.
【点评】此题主要考查了一元一次不等式的应用以及二元一次方程组的应用,根据题意得出总的进货费用是解题关键.
五.解答题(本大题共3题,每题9分,共27分)
23.【分析】(1)在y=kx+2中,只要x=0得y=2即可得点D的坐标为(0,2).
(2)由AP∥OD得Rt△PAC∽Rt△DOC,又=,可得==,故AP=6,BD=6﹣2=4,由S△PBD=4可得BP=2,把P(2,6)分别代入y=kx+2与y=可得一次函数解析式为:y=2x+2反比例函数解析式为:y=
(3)当x>0时,一次函数的值大于反比例函数的值的x的取值范围由图象能直接看出x>2.
【解答】解:(1)在y=kx+2中,令x=0得y=2,
∴点D的坐标为(0,2)
(2)∵AP∥OD,
∴∠CDO=∠CPA,∠COD=∠CAP,
∴Rt△PAC∽Rt△DOC,
∵=,即=,
∴==,
∴AP=6,
又∵BD=6﹣2=4,
∴由S△PBD=BP?BD=4,可得BP=2,
∴P(2,6)(4分)把P(2,6)分别代入y=kx+2与y=可得
一次函数解析式为:y=2x+2,
反比例函数解析式为:y=;
(3)由图可得x>2.
【点评】考查反比例函数和一次函数解析式的确定、图形的面积求法、相似三角形等知识及综合应用知识、解决问题的能力.有点难度.
24.【分析】(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD=AC=,证明△AEF∽△ODF,列比例式可得结论;
(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:,则=,求出r的值即可.
【解答】证明:(1)连接OD,如图1,
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)如图2,在⊙O中,∵∠E=∠B,
∴由(1)可知:∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵DH⊥AC,且点A是EH中点,
设AE=x,EC=4x,则AC=3x,
连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,
∵AB=AC,
∴D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,OD=AC=×3x=,
∵OD∥AC,
∴∠E=∠ODF,
在△AEF和△ODF中,
∵∠E=∠ODF,∠OFD=∠AFE,
∴△AEF∽△ODF,
∴,
∴==,
∴=;
(3)如图2,设⊙O的半径为r,即OD=OB=r,
∵EF=EA,
∴∠EFA=∠EAF,
∵OD∥EC,
∴∠FOD=∠EAF,
则∠FOD=∠EAF=∠EFA=∠OFD,
∴DF=OD=r,
∴DE=DF+EF=r+1,
∴BD=CD=DE=r+1,
在⊙O中,∵∠BDE=∠EAB,
∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形,
∴BF=BD=r+1,
∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,
在△BFD和△EFA中,
∵,
∴△BFD∽△EFA,
∴,
∴=,
解得:r1=,r2=(舍),
综上所述,⊙O的半径为.
【点评】本题是圆的综合题,考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、三角形相似的性质和判定、圆周角定理,第三问设圆的半径为r,根据等边对等角表示其它边长,利用比例列方程解决问题.
25.【分析】(1)根据已知条件得到∠AQP=45°,求得PQ=AP=2x,由于D为PQ中点,于是得到DQ=x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,由于D为PQ中点,得到DQ=x,求得GP=2x,列方程于是得到结论;
(3)如图②,当0<x≤时,根据正方形的面积公式得到y=x2;当<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=AB=2,根据正方形和三角形面积公式得到y关于x的函数解析式,求出最大值;当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到关系式即可.
【解答】解:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,
∴∠AQP=45°,
∴PQ=AP=2x,
∵D为PQ中点,
∴DQ=x,
故答案为:x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,
∵D为PQ中点,
∴DQ=x,
∴GP=x,
∴2x+x+2x=4,
∴x=;
(3)分三种情况:
如图②,当0<x≤时,y=S正方形DEFQ=DQ2=x2,
∴y=x2;
如图③,当<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=AB=2,
∵PQ=AP=2x,CK=2﹣2x,
∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,
∴y=S正方形DEFQ﹣S△MNF=DQ2﹣FM2,
∴y=x2﹣(5x﹣4)2=﹣x2+20x﹣8,
∴y=﹣x2+20x﹣8;
当x=﹣=时,y有最大值;
如图④,当1<x<2时,PQ=4﹣2x,
∴DQ=2﹣x,
∴y=S△DEQ=DQ2,
∴y=(2﹣x)2,
∴y=x2﹣2x+2;
综上所述,y关于x的函数解析式为y=x2(0<x≤)或y=﹣x2+20x﹣8(<x≤1)或y=x2﹣2x+2(1<x<2);
当x=时,y有最大值.
【点评】本题是四边形综合题目,考查了等腰直角三角形的性质,正方形的性质,图形面积的计算、二次函数、以及分类讨论等知识;正确的作出图形是解题的关键,注意分类讨论.
一、选择题(共10小题,每小题3分,满分30分)
1.下列图案中花边的内外边缘(每个图形边缘等宽)所围成的图形不相似的是( )
A. B. C. D.
2.下列方程中,关于x的一元二次方程是( )
A.(x﹣1)(x﹣2)=2 B. +=2
C.ax2+bx+c=0 D.3x2﹣2y=0
3.用配方法解一元二次方程x2+4x+3=0,下列配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=7 D.(x﹣2)2=7
4.下列关于反比例函数y=的说法正确的是( )
A.y随x的增大而增大
B.函数图象过点(2,)
C.图象位于第一、第三象限
D.x>0时,y随x的增大而增大
5.关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
A.q<16 B.q>16 C.q≤4 D.q≥4
6.半径为6,圆心角为120°的扇形的面积是( )
A.3π B.6π C.9π D.12π
7.线段a、b、c、d是成比例线段,a=4、b=2、c=2,则d的长为( )
A.1 B.2 C.3 D.4
8.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB1C1,若AC=2,则图中阴影部分的面积为( )
A. B. C. D.
9.如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC5O5的面积为( )
A.1cm2 B.2cm2 C. cm2 D. cm2
10.如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
二、填空题(本大题共6题,每小题4分,共24分)
11.(4分)一水塘里有鲤鱼、鲢鱼共10000尾,一渔民通过多次捕捞试验后发现,鲤鱼出现的频率为0.36,则水塘有鲤鱼 尾.
12.(4分)如图所示,它们是两个相似的平行四边形,根据条件可知,∠α= ,m= .
13.(4分)已知一元二次方程x2﹣3x﹣1=0的两根为x1、x2,x1+x2= .
14.(4分)已知:==,(b+d≠0)则= .
15.(4分)如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,4,9.则△ABC的面积是 .
16.(4分)如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△Bn?nMn的面积为Sn,则Sn= .(用含n的式子表示)
三.解答题(每题6分,共18分)
17.(6分)解方程:x2﹣6x+5=0 (配方法)
18.(6分)已知a=﹣3,b=2,求代数式的值.
19.(6分)如图,在Rt△ABC中,∠BAC=90°,∠C=30°.
(1)请在图中用尺规作图的方法作出AC的垂直平分线交BC于点D,并标出D点 (不写作法,保留作图痕迹).
(2)在(1)的条件下,连接AD,求证:△ABD是等边三角形.
四、解答题(每题7分,共21分)
20.(7分)有四张正面分别标有数字﹣2,﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们正面朝下,洗匀后从中抽出一张记下数字,放回洗匀后再从中抽出一张记下数字.
(1)请用列表或画树状图的方法表示两次抽出卡片上的数字的所有结果;
(2)若将第一次抽出的数字作为点的横坐标a,第二次抽出的数字作为点的纵坐标b,求点(a,b)落在双曲线上的概率.
21.(7分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
22.(7分)某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
五.解答题(本大题共3题,每题9分,共27分)
23.(9分)如图,一次函数y=kx+2的图象与反比例函数y=的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,=.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
24.(9分)如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求的值;
(3)若EA=EF=1,求圆O的半径.
25.(9分)如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)如图当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;并求出x为何值时,y为最大值.
2018-2019学年广东省汕头市龙湖实验中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(共10小题,每小题3分,满分30分)
1.【分析】根据相似图形的定义,结合图形,对选项一一分析,排除不符合要求答案.
【解答】解:A、两个不等边三角形形状相同,符合相似形的定义,故A选项不符合要求;
B、两个等边三角形形状相同,符合相似形的定义,故B选项不符合要求;
C、两个正方形形状相同,符合相似形的定义,故C选项不符合要求;
D、两个矩形,虽然四个角对应相等,但对应边不成比例,故D选项符合要求;
故选:D.
【点评】本题考查的是相似形的定义,联系图形,即形状相同,大小不一定相同的图形叫做相似形.
2.【分析】根据一元二次方程的定义:未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数,可得答案.
【解答】解:A、由原方程知:x2﹣3x+1=0,符合一元二次方程的定义,故本选项正确;
B、该方程是分式方程,故本选项错误;
C、当a=0时,该方程不是一元二次方程,故本选项错误;
D、该方程中含有两个未知数,是二元二次方程,故本选项错误;
故选:A.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
3.【分析】方程移项后,两边加上4变形即可得到结果.
【解答】解:方程移项得:x2+4x=﹣3,
配方得:x2+4x+4=1,即(x+2)2=1.
故选:A.
【点评】此题考查了解一元二次方程﹣配方法,熟练掌握完全平方公式是解本题的关键.
4.【分析】直接利用反比例函数的性质分别分析得出答案.
【解答】解:A、反比例函数y=,每个象限内,y随x的增大而增大,故此选项错误;
B、函数图象过点(2,﹣),故此选项错误;
C、函数图象图象位于第二、第四象限,故此选项错误;
D、x>0时,y随x的增大而增大,正确.
故选:D.
【点评】此题主要考查了反比例函数的性质,正确记忆相关性质是解题关键.
5.【分析】根据方程的系数结合根的判别式,即可得出△=64﹣4q>0,解之即可得出q的取值范围.
【解答】解:∵关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,
∴△=82﹣4q=64﹣4q>0,
解得:q<16.
故选:A.
【点评】本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键.
6.【分析】根据扇形的面积公式S=计算即可.
【解答】解:S==12π,
故选:D.
【点评】本题考查的是扇形面积的计算,掌握扇形的面积公式S=是解题的关键.
7.【分析】根据成比例线段的概念,得a:b=c:d,再根据比例的基本性质,可求得d的值.
【解答】解:∵a、b、c、d是成比例线段,
∴a:b=c:d,
即4:2=2:d,
∴d=1;
故选:A.
【点评】此题考查了比例线段,用到的知识点是比例线段的概念,在写的时候,注意按照字母的顺序.
8.【分析】根据题意,阴影部分为含30°锐角的直角三角形.已知长直角边可求短直角边长,再代入面积公式计算求解.
【解答】解:∵等腰直角△ABC绕点A逆时针旋转15°后得到△AB′C′,
∵∠CAC′=15°,
∴∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=2,
∴阴影部分的面积=×2×tan30°×2=,
故选:A.
【点评】此题考查旋转的性质及解直角三角形,掌握旋转的性质及三角函数的定义是解题的关键.
9.【分析】根据矩形的性质对角线互相平分可知O1是AC与DB的中点,根据等底同高得到S△ABO1=S矩形,又ABC1O1为平行四边形,根据平行四边形的性质对角线互相平分,得到O1O2=BO2,所以S△ABO2=S矩形,…,以此类推得到S△ABO5=S矩形,而S△ABO5等于平行四边形ABC5O5的面积的一半,根据矩形的面积即可求出平行四边形ABC5O5的面积.
【解答】解:∵设平行四边形ABC1O1的面积为S1,∴S△ABO1=S1,
又S△ABO1=S矩形,∴S1=S矩形=5=;
设ABC2O2为平行四边形为S2,∴S△ABO2=S2,
又S△ABO2=S矩形,∴S2=S矩形==;
,…,
同理:设ABC5O5为平行四边形为S5,S5==.
故选:D.
【点评】此题综合考查了矩形及平行四边形的性质,要求学生审清题意,找出面积之间的关系,归纳总结出一般性的结论.考查了学生观察、猜想、验证及归纳总结的能力.
10.【分析】作QD⊥AB,分点Q在AC、CB上运动这两种情况,由直角三角形的性质表示出QD的长,利用三角形面积公式得出函数解析式即可判断.
【解答】解:(1)过点Q作QD⊥AB于点D,
①如图1,当点Q在AC上运动时,即0≤x≤3,
由题意知AQ=x、AP=x,
∵∠A=45°,
∴QD=AQ=x,
则y=?x?x=x2;
②如图2,当点Q在CB上运动时,即3<x≤6,此时点P与点B重合,
由题意知BQ=6﹣x、AP=AB=3,
∵∠B=45°,
∴QD=BQ=(6﹣x),
则y=×3×(6﹣x)=﹣x+9;
故选:D.
【点评】本题主要考查动点问题的函数图象,解题的关键是根据题意弄清两点的运动路线,据此分类讨论并得出函数解析式.
二、填空题(本大题共6题,每小题4分,共24分)
11.【分析】由于水塘里有鲤鱼、鲢鱼共10000尾,而鲤鱼出现的频率为0.36,然后乘以总数即可得到水塘有鲤鱼有多少尾.
【解答】解:水塘约有鲤鱼10000×0.36=3600(尾),
故答案为:3600.
【点评】此题主要考查了利用频率估计概率的思想,首先通过实验得到事件的频率,然后即可估计事件的概率.
12.【分析】根据平行四边形的性质得到AB∥CD,AB=CD=m,根据相似多边形的性质列式计算,得到答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=m,
∴∠C=180°﹣55°=125°,
∵两个平行四边形相似,
∴α=∠C=125°,=,
解得,m=12,
故答案为:125°;12.
【点评】本题考查的是相似多边形的性质、平行四边形的性质,掌握相似多边形的对应角相等、对应边的比相等是解题的关键.
13.【分析】根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=﹣,代入计算即可.
【解答】解:∵一元二次方程x2﹣3x﹣1=0的两根是x1、x2,
∴x1+x2=3,
故答案为:3.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=﹣,x1?x2=.
14.【分析】分别设a为2m,c=2n,进而得到用m,n表示的b,d的值,把它们代入所给代数式求解即可.
【解答】解:设a为2m,c=2n,则b=5m,d=5n.
∴===,
故答案为.
【点评】考查等比性质的应用:若==k,则=k.
15.【分析】根据相似三角形的面积比是相似比的平方,先求出相似比.再根据平行四边形的性质及相似三角形的性质得到BC:DM=6:1,即S△ABC:S△FDM=36:1,从而得到△ABC面积.
【解答】解:过M作BC的平行线交AB、AC于D、E,
过M作AC的平行线交AB、BC于F、H,
过M作AB的平行线交AC、BC于I、G,
因为△1、△2、△3的面积比为1:4:9,
所以他们对应边边长的比为1:2:3,
又因为四边形BDMG与四边形CEMH为平行四边形,
所以DM=BG,EM=CH,
设DM为x,则ME=2x,GH=3x,
所以BC=BG+GH+CH=DM+GH+ME=x+2x+3x=6x,
所以BC:DM=6x:x=6:1,
由面积比等于相似比的平方故可得出:S△ABC:S△FDM=36:1,
所以S△ABC=36×S△FDM=36×1=36.
故答案为:36.
【点评】本题考查了平行线的性质,平行四边形的性质及相似三角形的性质.熟悉相似三角形的性质:相似三角形的面积比是相似比的平方.
16.【分析】利用相似三角形的性质求出Bn?n,再利用三角形的面积公式计算即可;
【解答】解:∵Bn?n∥B1C1,
∴△MnBn?n∽△MmB1C1,
∴=,
∴=,
∴Bn?n=,
∴Sn=××=,
故答案为.
【点评】本题考查相似三角形的判定和性质、正方形的性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
三.解答题(每题6分,共18分)
17.【分析】利用配方法解方程.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
【解答】解:由原方程移项,得
x2﹣6x=﹣5,
等式两边同时加上一次项系数一半的平方32.得
x2﹣6x+32=﹣5+32,即(x﹣3)2=4,
∴x=3±2,
∴原方程的解是:x1=5,x2=1.
【点评】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
18.【分析】将所求式子括号中的两项通分并利用同分母分式的减法法则计算,后一项分子利用完全平方式分解因式后约分,得到最简结果,然后将a与b的值代入化简后的式子中计算,即可得到所求式子的值.
【解答】解:
=÷
=÷(a+b)
=,
当a=﹣3,b=2时,
原式==﹣.
【点评】此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应先将多项式分解因式后再约分.
19.【分析】(1)作线段AC的垂直平分线即可;
(2)根据线段垂直平分线的性质可得DA=DC,根据等边对等角可得∠CAD=∠C,进而可得∠ADB=∠B=∠DAB=60°,然后可得答案.
【解答】解:(1)如图所示:
(2)∵∠BAC=90°,∠C=30°
∴∠B=60°,
又∵点D在AC的垂直平分线上,
∴DA=DC,
∴∠CAD=∠C=30°,
∴∠DAB=60°,
∴∠ADB=∠B=∠DAB=60°,
即△ABD是等边三角形.
【点评】此题主要考查了基本作图,以及线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
四、解答题(每题7分,共21分)
20.【分析】(1)列表得出所有等可能的情况数即可;
(2)找出在双曲线y=上的点的情况数,即可求出所求的概率.
【解答】解:(1)列表如下:
﹣2 ﹣1 1 2
﹣2 ﹣2,﹣2 ﹣2,﹣1 ﹣2,1 ﹣2,2
﹣1 ﹣1,﹣2 ﹣1,﹣1 ﹣1,1 ﹣1,2
1 1,﹣2 1,﹣1 1,1 1,2
2 2,﹣2 2,﹣1 2,1 2,2
由上表可知,两次抽出卡片上的数字的所有结果一共有16种;
(2)∵上述16种结果出现的可能性相同,且在双曲线y=上的点有四个,它们分别是(﹣2,﹣1),(﹣1,﹣2),(1,2),(2,1),
∴点(a,b)落在双曲线y=上的概率P==.
【点评】此题考查了列表法与树状图法,以及反比例函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.
21.【分析】(1)首先证明AB=AF=AD,然后再证明∠AFG=90°,接下来,依据HL可证明△ABG≌△AFG;
(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可.
【解答】解:(1)在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
,
∴△ABG≌△AFG(HL);
(2)∵△ABG≌△AFG,
∴BG=FG,
设BG=FG=x,则GC=6﹣x,
∵E为CD的中点,
∴CE=EF=DE=3,
∴EG=3+x,
∴在Rt△CEG中,32+(6﹣x)2=(3+x)2,解得x=2,
∴BG=2.
【点评】此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.
22.【分析】(1)首先设A种型号计算器的销售价格是x元,A种型号计算器的销售价格是y元,根据题意可等量关系:①5台A型号和1台B型号计算器,可获利润76元;②销售6台A型号和3台B型号计算器,可获利润120元,根据等量关系列出方程组,再解即可;
(2)根据题意表示出所用成本,进而得出不等式求出即可.
【解答】解:(1)设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y元,由题意得:
,
解得:;
答:A种型号计算器的销售价格是42元,B种型号计算器的销售价格是56元;
(2)设购进A型计算器a台,则购进B型计算器:(70﹣a)台,
则30a+40(70﹣a)≤2500,
解得:a≥30,
答:最少需要购进A型号的计算器30台.
【点评】此题主要考查了一元一次不等式的应用以及二元一次方程组的应用,根据题意得出总的进货费用是解题关键.
五.解答题(本大题共3题,每题9分,共27分)
23.【分析】(1)在y=kx+2中,只要x=0得y=2即可得点D的坐标为(0,2).
(2)由AP∥OD得Rt△PAC∽Rt△DOC,又=,可得==,故AP=6,BD=6﹣2=4,由S△PBD=4可得BP=2,把P(2,6)分别代入y=kx+2与y=可得一次函数解析式为:y=2x+2反比例函数解析式为:y=
(3)当x>0时,一次函数的值大于反比例函数的值的x的取值范围由图象能直接看出x>2.
【解答】解:(1)在y=kx+2中,令x=0得y=2,
∴点D的坐标为(0,2)
(2)∵AP∥OD,
∴∠CDO=∠CPA,∠COD=∠CAP,
∴Rt△PAC∽Rt△DOC,
∵=,即=,
∴==,
∴AP=6,
又∵BD=6﹣2=4,
∴由S△PBD=BP?BD=4,可得BP=2,
∴P(2,6)(4分)把P(2,6)分别代入y=kx+2与y=可得
一次函数解析式为:y=2x+2,
反比例函数解析式为:y=;
(3)由图可得x>2.
【点评】考查反比例函数和一次函数解析式的确定、图形的面积求法、相似三角形等知识及综合应用知识、解决问题的能力.有点难度.
24.【分析】(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD=AC=,证明△AEF∽△ODF,列比例式可得结论;
(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:,则=,求出r的值即可.
【解答】证明:(1)连接OD,如图1,
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)如图2,在⊙O中,∵∠E=∠B,
∴由(1)可知:∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵DH⊥AC,且点A是EH中点,
设AE=x,EC=4x,则AC=3x,
连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,
∵AB=AC,
∴D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,OD=AC=×3x=,
∵OD∥AC,
∴∠E=∠ODF,
在△AEF和△ODF中,
∵∠E=∠ODF,∠OFD=∠AFE,
∴△AEF∽△ODF,
∴,
∴==,
∴=;
(3)如图2,设⊙O的半径为r,即OD=OB=r,
∵EF=EA,
∴∠EFA=∠EAF,
∵OD∥EC,
∴∠FOD=∠EAF,
则∠FOD=∠EAF=∠EFA=∠OFD,
∴DF=OD=r,
∴DE=DF+EF=r+1,
∴BD=CD=DE=r+1,
在⊙O中,∵∠BDE=∠EAB,
∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形,
∴BF=BD=r+1,
∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,
在△BFD和△EFA中,
∵,
∴△BFD∽△EFA,
∴,
∴=,
解得:r1=,r2=(舍),
综上所述,⊙O的半径为.
【点评】本题是圆的综合题,考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、三角形相似的性质和判定、圆周角定理,第三问设圆的半径为r,根据等边对等角表示其它边长,利用比例列方程解决问题.
25.【分析】(1)根据已知条件得到∠AQP=45°,求得PQ=AP=2x,由于D为PQ中点,于是得到DQ=x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,由于D为PQ中点,得到DQ=x,求得GP=2x,列方程于是得到结论;
(3)如图②,当0<x≤时,根据正方形的面积公式得到y=x2;当<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=AB=2,根据正方形和三角形面积公式得到y关于x的函数解析式,求出最大值;当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到关系式即可.
【解答】解:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,
∴∠AQP=45°,
∴PQ=AP=2x,
∵D为PQ中点,
∴DQ=x,
故答案为:x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,
∵D为PQ中点,
∴DQ=x,
∴GP=x,
∴2x+x+2x=4,
∴x=;
(3)分三种情况:
如图②,当0<x≤时,y=S正方形DEFQ=DQ2=x2,
∴y=x2;
如图③,当<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=AB=2,
∵PQ=AP=2x,CK=2﹣2x,
∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,
∴y=S正方形DEFQ﹣S△MNF=DQ2﹣FM2,
∴y=x2﹣(5x﹣4)2=﹣x2+20x﹣8,
∴y=﹣x2+20x﹣8;
当x=﹣=时,y有最大值;
如图④,当1<x<2时,PQ=4﹣2x,
∴DQ=2﹣x,
∴y=S△DEQ=DQ2,
∴y=(2﹣x)2,
∴y=x2﹣2x+2;
综上所述,y关于x的函数解析式为y=x2(0<x≤)或y=﹣x2+20x﹣8(<x≤1)或y=x2﹣2x+2(1<x<2);
当x=时,y有最大值.
【点评】本题是四边形综合题目,考查了等腰直角三角形的性质,正方形的性质,图形面积的计算、二次函数、以及分类讨论等知识;正确的作出图形是解题的关键,注意分类讨论.
同课章节目录
