高中物理粤教版必修一学案 第二章+实验:研究匀变速直线运动+Word版含答案
文档属性
| 名称 | 高中物理粤教版必修一学案 第二章+实验:研究匀变速直线运动+Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 319.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-04-19 22:10:39 | ||
图片预览



文档简介
实验:研究匀变速直线运动
一、实验目的
1.进一步练习使用打点计时器及利用纸带求瞬时速度。
2.学会用实验研究匀变速直线运动的规律的方法,学会用v-t图象处理实验数据。
二、实验原理
1.利用纸带计算瞬时速度:以纸带上某点为中间时刻取一小段位移,用这段位移的平均速度表示这点的瞬时速度。
2.用v-t图象表示小车的运动情况:以速度v为纵轴、时间t为横轴建立直角坐标系,用描点法画出小车的v-t图象,图线的倾斜程度表示加速度的大小,如果v-t图象是一条倾斜的直线,说明小车的速度是均匀变化的。
三、实验器材
打点计时器、交流电源、纸带、一端附有滑轮的长木板、小车、细绳、钩码、刻度尺、坐标纸。
四、实验步骤
1.如图1所示,把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,打点计时器固定在长木板没有滑轮的一端,连接好电路。
图1
2.把一条细绳拴在小车上,使细绳跨过滑轮,下面挂上适当的钩码,把纸带穿过打点计时器,并把纸带的另一端固定在小车的后面。
3.把小车停在靠近打点计时器的位置,先接通电源,后释放小车,让小车拖着纸带运动,打点计时器就在纸带上打下一行小点,随后立即关闭电源。
4.换上新纸带,重复实验三次。
五、数据处理
1.测量并记录数据
(1)从几条纸带中选择一条点迹最清晰的。舍掉开头一些过于密集的点迹,找一个适当的点当作计时起点(0点),每5个点(相隔0.1 s)取一个计数点进行测量,如图2所示(相邻两点间还有四个点未画出)。标明0、1、2、3、4、…,测量各计数点到0点的距离s,并记录填入表中。
图2
位置编号
0
1
2
3
4
5
t/s
s/m
v/(m·s-1)
(2)分别计算出相邻的两计数点之间的距离s1、s2、s3…。
(3)利用一段时间内的平均速度等于这段时间中间时刻的瞬时速度,即vn=。例如,图中计数点4的速度v4=。并将求得的各计数点1、2、3、4、5的瞬时速度,填入上面的表格中。
2.作出v-t图象分析运动规律
(1)在坐标纸上建立直角坐标系,横轴表示时间,纵轴表示速度,并根据表格中的数据在坐标系中描点。
(2)画一条直线,让这条直线通过尽可能多的点,不在线上的点均匀分布在直线的两侧,偏差比较大的点忽略不计,如图3所示。
图3
(3)观察所得到的直线,分析物体的速度随时间的变化规律。
(4)根据v-t图象求出小车运动的加速度a=。
六、注意事项
1.开始释放小车时,应使小车靠近打点计时器。
2.先接通电源,等打点稳定后,再释放小车。
3.打点完毕,立即关闭电源。
4.选取一条点迹清晰的纸带,适当舍弃点迹密集部分,适当选取计数点(注意计数点与计时点的区别),弄清楚所选的时间间隔T等于多少。
5.要逐次测量各段距离,应尽可能地一次测量完毕。
6.在坐标纸上画v-t图象时,注意坐标轴单位长度的选取,应使图象尽量分布在坐标平面中央。
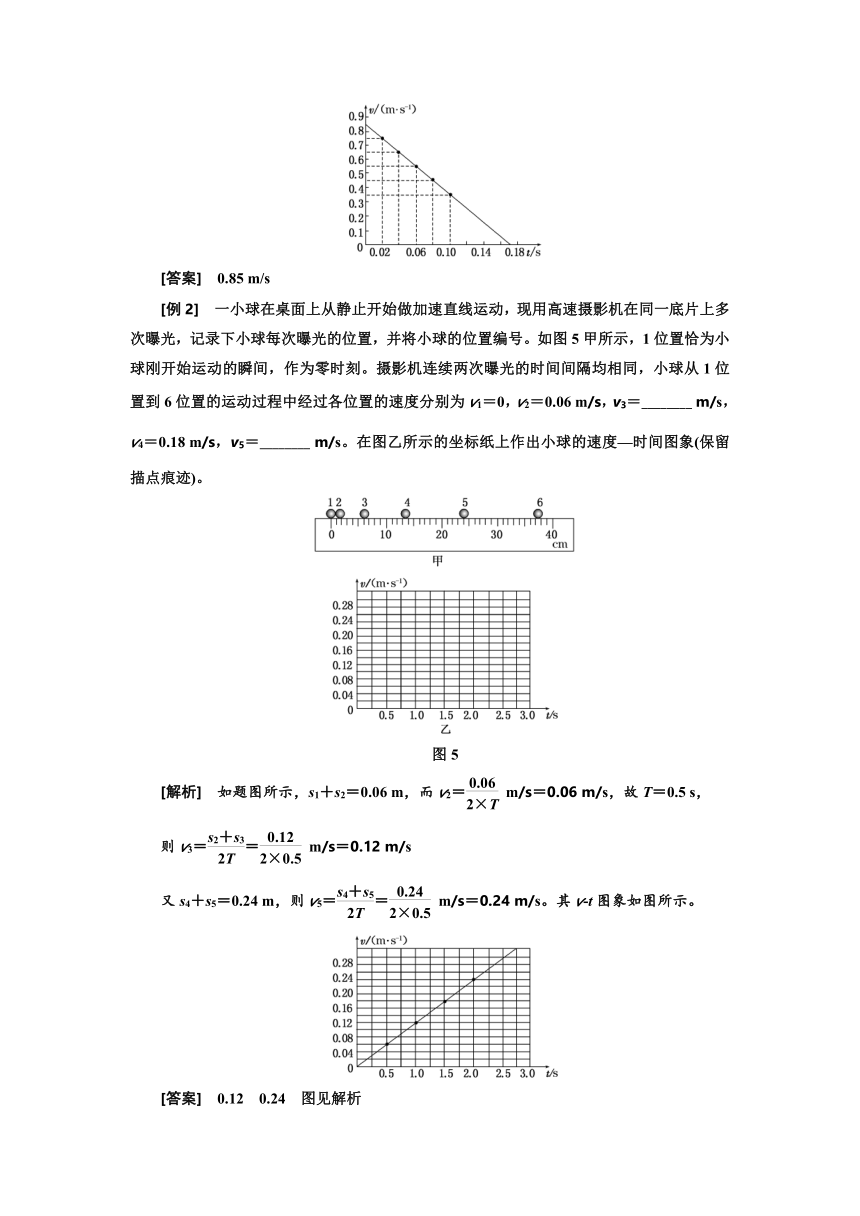
[例1] 如图4甲所示,用打点计时器记录小车的运动情况。小车开始在水平玻璃板上运动,后来在薄布面上做减速运动。所打出的纸带及相邻两点间的距离(单位:cm)如图乙所示,纸带上相邻两点间对应的时间间隔为0.02 s。试用作图法(v-t图象)求出小车在玻璃板上的运动速度。
图4
[解析] 设对应点1、2、3、4、5的瞬时速度分别为v1、v2、v3、v4、v5,则有
v1= cm/s=75 cm/s=0.75 m/s,
v2= cm/s=65 cm/s=0.65 m/s,
v3= cm/s=55 cm/s=0.55 m/s,
v4= cm/s=45 cm/s=0.45 m/s,
v5= cm/s=35 cm/s=0.35 m/s,
以速度为纵坐标,以时间为横坐标建立直角坐标系。用描点法作出小车在薄布上做减速运动时的v-t图象。将图象延长,使其与纵轴相交,如图所示。由图象可知,小车做减速运动的初速度为0.85 m/s,即为小车在玻璃板上的运动速度。
[答案] 0.85 m/s
[例2] 一小球在桌面上从静止开始做加速直线运动,现用高速摄影机在同一底片上多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图5甲所示,1位置恰为小球刚开始运动的瞬间,作为零时刻。摄影机连续两次曝光的时间间隔均相同,小球从1位置到6位置的运动过程中经过各位置的速度分别为v1=0,v2=0.06 m/s,v3=________ m/s,v4=0.18 m/s,v5=________ m/s。在图乙所示的坐标纸上作出小球的速度—时间图象(保留描点痕迹)。
图5
[解析] 如题图所示,s1+s2=0.06 m,而v2= m/s=0.06 m/s,故T=0.5 s,
则v3== m/s=0.12 m/s
又s4+s5=0.24 m,则v5== m/s=0.24 m/s。其v-t图象如图所示。
[答案] 0.12 0.24 图见解析
1.(多选)在做“研究匀变速直线运动”的实验时,下列方法中有利于减小实验误差的是( )
A.选取计数点,把每5个点的时间间隔作为一个时间单位
B.使小车运动的加速度尽量小些
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的那一部分点进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
解析:选ACD 把每打五个点的时间间隔作为一个时间单位,这样可以增加测量点间的距离,减小测量过程所产生的误差,A正确。小车的加速度过小,则物体运动间距太密集,测量误差较大,B错误。纸带上密集的点,点间间距过小,测量误差较大,应舍去而只利用点迹清晰、点间间隔适当的那部分进行测量、计算,C正确。选用各处平整程度相同的长木板做实验,这样受力均匀,加速度变化小,实验误差小,D正确。
2.(多选)如图6甲、乙所示为同一打点计时器打出的两条纸带,由纸带可知( )
图6
A.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的大
B.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的小
C.纸带甲的加速度比乙的大
D.纸带甲的加速度比乙的小
解析:选BD 由题图纸带可以看出,打下计数点“0”至“5”的过程中,甲的位移比乙的小,而经历的时间相等,则甲的平均速度小于乙的平均速度,故A错误,B正确。纸带甲点迹均匀,则其加速度为零,而纸带乙的速度减小,加速度不为零,故C错误,D正确。
3.在“研究匀变速直线运动”的实验中:
(1)下列哪些器材是多余的:____________________________________。
①电磁打点计时器 ②天平 ③低压直流电源 ④细绳
⑤纸带 ⑥小车 ⑦钩码 ⑧秒表 ⑨一端有滑轮的长木板
(2)为达到实验目的,还需要的器材是:____________________________________。
解析:实验中给电磁打点计时器供电的是低压交流电源,而非低压直流电源。实验中小车的运动时间可以从所打纸带上得出,而不使用秒表测量,另外此实验不需要测质量。在此实验中还需用刻度尺测量计数点间的距离。
答案:(1)②③⑧ (2)低压交流电源、刻度尺
4.在“研究匀变速直线运动”的实验中,电火花打点计时器使用的交流电源频率为50 Hz,记录小车运动的纸带如图7甲所示,在纸带上选择标为0~6的计数点,相邻两个计数点间还有四个计时点未画出,纸带旁边并排放着毫米刻度尺,零刻度点跟0计数点对齐。
(1)请你根据放大的图片计算出打2和4两个计数点时的速度v2=_______ m/s、v4=________ m/s(均保留2位有效数字),已知v1=0.15 m/s,v3=0.22 m/s,v5=0.39 m/s,请根据数据在图乙上作v-t图。
(2)电源频率低于50 Hz时,若仍按照50 Hz计算,则测出的速度值将比真实值________。(选填“大”或者“小”)
图7
解析:(1)v2== m/s=0.21 m/s
v4== m/s=0.33 m/s
根据各速度值作v-t图如图所示
(2)当电源的频率为50 Hz时,打点计时器每隔0.02 s打一个点;当交流电源的频率低于50 Hz时,打点的时间间隔将大于0.02 s,若计算速度时仍按0.02 s计算,由=可得,测出的速度值大于真实值。
答案:(1)0.21 0.33 v-t图见解析 (2)大
5.在用电火花计时器“研究匀变速直线运动”的实验中,小车在恒定外力作用下运动,如图8甲所示是一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间还有四个点未画出。所用电源的频率为50 Hz。
图8
(1)由纸带根据运动学有关公式可求得vB=1.38 m/s,vC=________ m/s,vD=3.90 m/s。
(2)利用纸带上的数据求出小车运动的加速度a=______ m/s2。
(3)若实验中以打A点时开始计时,利用所得的数据在图乙中作出小车的v-t图线,将图线延长线与纵轴相交,此交点纵轴坐标的物理意义是____________________________。
解析:(1)电源频率为50 Hz,则周期为0.02 s,相邻计数点间还有四个点未画出,则可知相邻计数点间的时间间隔为T=0.02×5 s=0.1 s,C点的瞬时速度为
vC== m/s=2.64 m/s。
(2)纸带加速度为a=== m/s2=12.6 m/s2。
(3)用描点法作出小车的v-t图线,将图线延长与纵轴相交,此交点纵轴坐标的物理意义是打点计时器开始计时时的速度,即打下A点时纸带对应的速度。
答案:(1)2.64 (2)12.6
(3)
开始计时时,小车的速度(或vA)
6.在做“匀加速直线运动的实验探究”的实验中,打点计时器接在50 Hz的低压交变电源上,某同学在打出的纸带上每5点取一个计数点,共取了A、B、C、D、E、F六个计数点(每相邻两个计数点间的四个点未画出)。从每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由短到长紧靠但不重叠地粘在xOy坐标系中,如图9所示,由此可以得到一条表示v-t关系的图线,从而求出加速度的大小。
图9
(1)请你在xOy坐标系中用最简洁的方法作出能表示v-t关系的图线(作答在图上),其________(填“x”或“y”)轴相当于v轴。
(2)从第一个计数点开始计时,为求出0.15 s时刻的瞬时速度,需要测出________段纸带的长度。
(3)若测得a段纸带的长度为2.0 cm,e段纸带的长度为10.0 cm,则可求出加速度的大小为________m/s2。
解析:(1)分别取a、b、c、d、e五段的上方中点,并连线,得到的即为v-t图象,如图所示,y轴相当于v轴。
(2)t=0.15 s是BC时间段的中间时刻,要求t=0.15 s时的瞬时速度,只需要测b纸带的长度sb,然后用=即可求得t=0.15 s时的速度。
(3)a、e段各自中间时刻的速度分别为va=,ve=,根据a=得a=2 m/s2。
答案:(1)图见解析 y (2)b (3)2
7.某同学用如图10甲所示的装置研究自由落体运动,所打的纸带如图乙所示。
甲
乙
图10
(1)实验时纸带的________端应和重物相连接(选填“A”或“B”)。
(2)纸带上1至9各点为计时点,由纸带所示数据可算出当地的重力加速度为________ m/s2。
(3)当地的重力加速度为9.8 m/s2,请列出测量值与当地重力加速度值有差异的一个原因_________________________________________________________________________。
解析:(1)由自由落体运动规律知,在连续相等时间内物体的位移越来越大,故B端应和重物相连接。
(2)Δs=ngT2,又Δs=3.92 cm-2.04 cm=1.88×10-2 m,n=5,T=0.02 s,故g=9.4 m/s2。
答案:(1)B (2)9.4
(3)纸带与墨粉纸盘及其他接触物间存在摩擦
一、实验目的
1.进一步练习使用打点计时器及利用纸带求瞬时速度。
2.学会用实验研究匀变速直线运动的规律的方法,学会用v-t图象处理实验数据。
二、实验原理
1.利用纸带计算瞬时速度:以纸带上某点为中间时刻取一小段位移,用这段位移的平均速度表示这点的瞬时速度。
2.用v-t图象表示小车的运动情况:以速度v为纵轴、时间t为横轴建立直角坐标系,用描点法画出小车的v-t图象,图线的倾斜程度表示加速度的大小,如果v-t图象是一条倾斜的直线,说明小车的速度是均匀变化的。
三、实验器材
打点计时器、交流电源、纸带、一端附有滑轮的长木板、小车、细绳、钩码、刻度尺、坐标纸。
四、实验步骤
1.如图1所示,把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,打点计时器固定在长木板没有滑轮的一端,连接好电路。
图1
2.把一条细绳拴在小车上,使细绳跨过滑轮,下面挂上适当的钩码,把纸带穿过打点计时器,并把纸带的另一端固定在小车的后面。
3.把小车停在靠近打点计时器的位置,先接通电源,后释放小车,让小车拖着纸带运动,打点计时器就在纸带上打下一行小点,随后立即关闭电源。
4.换上新纸带,重复实验三次。
五、数据处理
1.测量并记录数据
(1)从几条纸带中选择一条点迹最清晰的。舍掉开头一些过于密集的点迹,找一个适当的点当作计时起点(0点),每5个点(相隔0.1 s)取一个计数点进行测量,如图2所示(相邻两点间还有四个点未画出)。标明0、1、2、3、4、…,测量各计数点到0点的距离s,并记录填入表中。
图2
位置编号
0
1
2
3
4
5
t/s
s/m
v/(m·s-1)
(2)分别计算出相邻的两计数点之间的距离s1、s2、s3…。
(3)利用一段时间内的平均速度等于这段时间中间时刻的瞬时速度,即vn=。例如,图中计数点4的速度v4=。并将求得的各计数点1、2、3、4、5的瞬时速度,填入上面的表格中。
2.作出v-t图象分析运动规律
(1)在坐标纸上建立直角坐标系,横轴表示时间,纵轴表示速度,并根据表格中的数据在坐标系中描点。
(2)画一条直线,让这条直线通过尽可能多的点,不在线上的点均匀分布在直线的两侧,偏差比较大的点忽略不计,如图3所示。
图3
(3)观察所得到的直线,分析物体的速度随时间的变化规律。
(4)根据v-t图象求出小车运动的加速度a=。
六、注意事项
1.开始释放小车时,应使小车靠近打点计时器。
2.先接通电源,等打点稳定后,再释放小车。
3.打点完毕,立即关闭电源。
4.选取一条点迹清晰的纸带,适当舍弃点迹密集部分,适当选取计数点(注意计数点与计时点的区别),弄清楚所选的时间间隔T等于多少。
5.要逐次测量各段距离,应尽可能地一次测量完毕。
6.在坐标纸上画v-t图象时,注意坐标轴单位长度的选取,应使图象尽量分布在坐标平面中央。
[例1] 如图4甲所示,用打点计时器记录小车的运动情况。小车开始在水平玻璃板上运动,后来在薄布面上做减速运动。所打出的纸带及相邻两点间的距离(单位:cm)如图乙所示,纸带上相邻两点间对应的时间间隔为0.02 s。试用作图法(v-t图象)求出小车在玻璃板上的运动速度。
图4
[解析] 设对应点1、2、3、4、5的瞬时速度分别为v1、v2、v3、v4、v5,则有
v1= cm/s=75 cm/s=0.75 m/s,
v2= cm/s=65 cm/s=0.65 m/s,
v3= cm/s=55 cm/s=0.55 m/s,
v4= cm/s=45 cm/s=0.45 m/s,
v5= cm/s=35 cm/s=0.35 m/s,
以速度为纵坐标,以时间为横坐标建立直角坐标系。用描点法作出小车在薄布上做减速运动时的v-t图象。将图象延长,使其与纵轴相交,如图所示。由图象可知,小车做减速运动的初速度为0.85 m/s,即为小车在玻璃板上的运动速度。
[答案] 0.85 m/s
[例2] 一小球在桌面上从静止开始做加速直线运动,现用高速摄影机在同一底片上多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图5甲所示,1位置恰为小球刚开始运动的瞬间,作为零时刻。摄影机连续两次曝光的时间间隔均相同,小球从1位置到6位置的运动过程中经过各位置的速度分别为v1=0,v2=0.06 m/s,v3=________ m/s,v4=0.18 m/s,v5=________ m/s。在图乙所示的坐标纸上作出小球的速度—时间图象(保留描点痕迹)。
图5
[解析] 如题图所示,s1+s2=0.06 m,而v2= m/s=0.06 m/s,故T=0.5 s,
则v3== m/s=0.12 m/s
又s4+s5=0.24 m,则v5== m/s=0.24 m/s。其v-t图象如图所示。
[答案] 0.12 0.24 图见解析
1.(多选)在做“研究匀变速直线运动”的实验时,下列方法中有利于减小实验误差的是( )
A.选取计数点,把每5个点的时间间隔作为一个时间单位
B.使小车运动的加速度尽量小些
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的那一部分点进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
解析:选ACD 把每打五个点的时间间隔作为一个时间单位,这样可以增加测量点间的距离,减小测量过程所产生的误差,A正确。小车的加速度过小,则物体运动间距太密集,测量误差较大,B错误。纸带上密集的点,点间间距过小,测量误差较大,应舍去而只利用点迹清晰、点间间隔适当的那部分进行测量、计算,C正确。选用各处平整程度相同的长木板做实验,这样受力均匀,加速度变化小,实验误差小,D正确。
2.(多选)如图6甲、乙所示为同一打点计时器打出的两条纸带,由纸带可知( )
图6
A.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的大
B.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的小
C.纸带甲的加速度比乙的大
D.纸带甲的加速度比乙的小
解析:选BD 由题图纸带可以看出,打下计数点“0”至“5”的过程中,甲的位移比乙的小,而经历的时间相等,则甲的平均速度小于乙的平均速度,故A错误,B正确。纸带甲点迹均匀,则其加速度为零,而纸带乙的速度减小,加速度不为零,故C错误,D正确。
3.在“研究匀变速直线运动”的实验中:
(1)下列哪些器材是多余的:____________________________________。
①电磁打点计时器 ②天平 ③低压直流电源 ④细绳
⑤纸带 ⑥小车 ⑦钩码 ⑧秒表 ⑨一端有滑轮的长木板
(2)为达到实验目的,还需要的器材是:____________________________________。
解析:实验中给电磁打点计时器供电的是低压交流电源,而非低压直流电源。实验中小车的运动时间可以从所打纸带上得出,而不使用秒表测量,另外此实验不需要测质量。在此实验中还需用刻度尺测量计数点间的距离。
答案:(1)②③⑧ (2)低压交流电源、刻度尺
4.在“研究匀变速直线运动”的实验中,电火花打点计时器使用的交流电源频率为50 Hz,记录小车运动的纸带如图7甲所示,在纸带上选择标为0~6的计数点,相邻两个计数点间还有四个计时点未画出,纸带旁边并排放着毫米刻度尺,零刻度点跟0计数点对齐。
(1)请你根据放大的图片计算出打2和4两个计数点时的速度v2=_______ m/s、v4=________ m/s(均保留2位有效数字),已知v1=0.15 m/s,v3=0.22 m/s,v5=0.39 m/s,请根据数据在图乙上作v-t图。
(2)电源频率低于50 Hz时,若仍按照50 Hz计算,则测出的速度值将比真实值________。(选填“大”或者“小”)
图7
解析:(1)v2== m/s=0.21 m/s
v4== m/s=0.33 m/s
根据各速度值作v-t图如图所示
(2)当电源的频率为50 Hz时,打点计时器每隔0.02 s打一个点;当交流电源的频率低于50 Hz时,打点的时间间隔将大于0.02 s,若计算速度时仍按0.02 s计算,由=可得,测出的速度值大于真实值。
答案:(1)0.21 0.33 v-t图见解析 (2)大
5.在用电火花计时器“研究匀变速直线运动”的实验中,小车在恒定外力作用下运动,如图8甲所示是一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间还有四个点未画出。所用电源的频率为50 Hz。
图8
(1)由纸带根据运动学有关公式可求得vB=1.38 m/s,vC=________ m/s,vD=3.90 m/s。
(2)利用纸带上的数据求出小车运动的加速度a=______ m/s2。
(3)若实验中以打A点时开始计时,利用所得的数据在图乙中作出小车的v-t图线,将图线延长线与纵轴相交,此交点纵轴坐标的物理意义是____________________________。
解析:(1)电源频率为50 Hz,则周期为0.02 s,相邻计数点间还有四个点未画出,则可知相邻计数点间的时间间隔为T=0.02×5 s=0.1 s,C点的瞬时速度为
vC== m/s=2.64 m/s。
(2)纸带加速度为a=== m/s2=12.6 m/s2。
(3)用描点法作出小车的v-t图线,将图线延长与纵轴相交,此交点纵轴坐标的物理意义是打点计时器开始计时时的速度,即打下A点时纸带对应的速度。
答案:(1)2.64 (2)12.6
(3)
开始计时时,小车的速度(或vA)
6.在做“匀加速直线运动的实验探究”的实验中,打点计时器接在50 Hz的低压交变电源上,某同学在打出的纸带上每5点取一个计数点,共取了A、B、C、D、E、F六个计数点(每相邻两个计数点间的四个点未画出)。从每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由短到长紧靠但不重叠地粘在xOy坐标系中,如图9所示,由此可以得到一条表示v-t关系的图线,从而求出加速度的大小。
图9
(1)请你在xOy坐标系中用最简洁的方法作出能表示v-t关系的图线(作答在图上),其________(填“x”或“y”)轴相当于v轴。
(2)从第一个计数点开始计时,为求出0.15 s时刻的瞬时速度,需要测出________段纸带的长度。
(3)若测得a段纸带的长度为2.0 cm,e段纸带的长度为10.0 cm,则可求出加速度的大小为________m/s2。
解析:(1)分别取a、b、c、d、e五段的上方中点,并连线,得到的即为v-t图象,如图所示,y轴相当于v轴。
(2)t=0.15 s是BC时间段的中间时刻,要求t=0.15 s时的瞬时速度,只需要测b纸带的长度sb,然后用=即可求得t=0.15 s时的速度。
(3)a、e段各自中间时刻的速度分别为va=,ve=,根据a=得a=2 m/s2。
答案:(1)图见解析 y (2)b (3)2
7.某同学用如图10甲所示的装置研究自由落体运动,所打的纸带如图乙所示。
甲
乙
图10
(1)实验时纸带的________端应和重物相连接(选填“A”或“B”)。
(2)纸带上1至9各点为计时点,由纸带所示数据可算出当地的重力加速度为________ m/s2。
(3)当地的重力加速度为9.8 m/s2,请列出测量值与当地重力加速度值有差异的一个原因_________________________________________________________________________。
解析:(1)由自由落体运动规律知,在连续相等时间内物体的位移越来越大,故B端应和重物相连接。
(2)Δs=ngT2,又Δs=3.92 cm-2.04 cm=1.88×10-2 m,n=5,T=0.02 s,故g=9.4 m/s2。
答案:(1)B (2)9.4
(3)纸带与墨粉纸盘及其他接触物间存在摩擦
同课章节目录
- 第一章 运动的描述
- 第一节 认识运动
- 第二节 时间 位移
- 第三节 记录物体的运动信息
- 第四节 物体运动的速度
- 第五节 速度变化的快慢 加速度
- 第六节 用图象描述直线运动
- 第二章 探究匀变速直线运动规律
- 第一节 探究自由落体运动
- 第二节 自由落体运动规律
- 第三节 从自由落体到匀变速直线运动
- 第四节 匀变速直线运动与汽车行驶安全
- 第三章 研究物体间的相互作用
- 第一节 探究形变与弹力的关系
- 第二节 研究摩擦力
- 第三节 力的等效和替代
- 第四节 力的合成与分解
- 第五节 共点力的平衡条件
- 第六节 作用力与反作用力
- 第四章 力与运动
- 第一节 伽利略的理想实验与牛顿第一定律
- 第二节 影响加速度的因素
- 第三节 探究物体运动与受力的关系
- 第四节 牛顿第二定律
- 第五节 牛顿第二定律的应用
- 第六节 超重和失重
- 第七节 力学单位
