华东师大版数学八年级下册20.3.1方差课件 共20张PPT
文档属性
| 名称 | 华东师大版数学八年级下册20.3.1方差课件 共20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览




文档简介
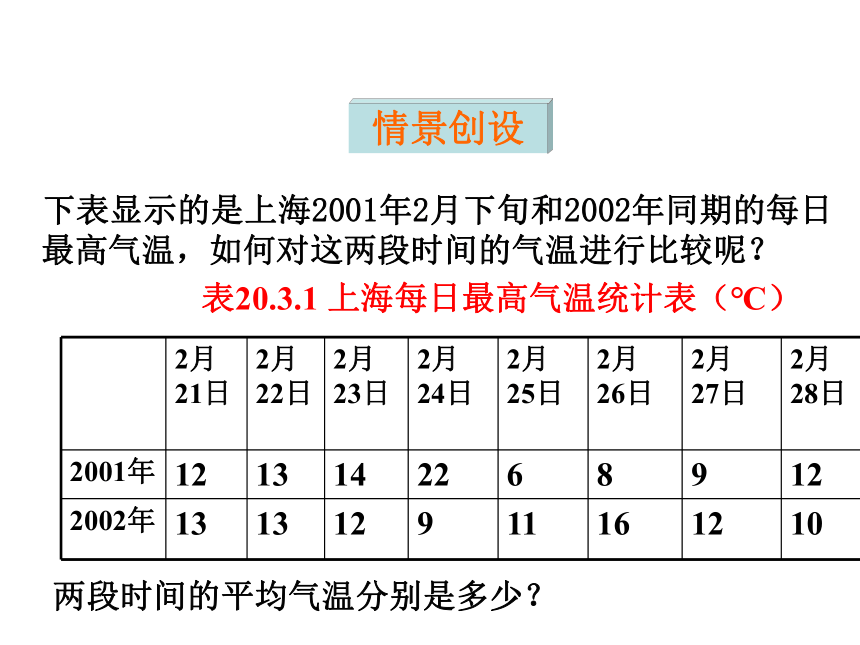
课件20张PPT。课堂小结情景创设探索发现例题解析随堂练习课堂检测20.3.1 方差 下表显示的是上海2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
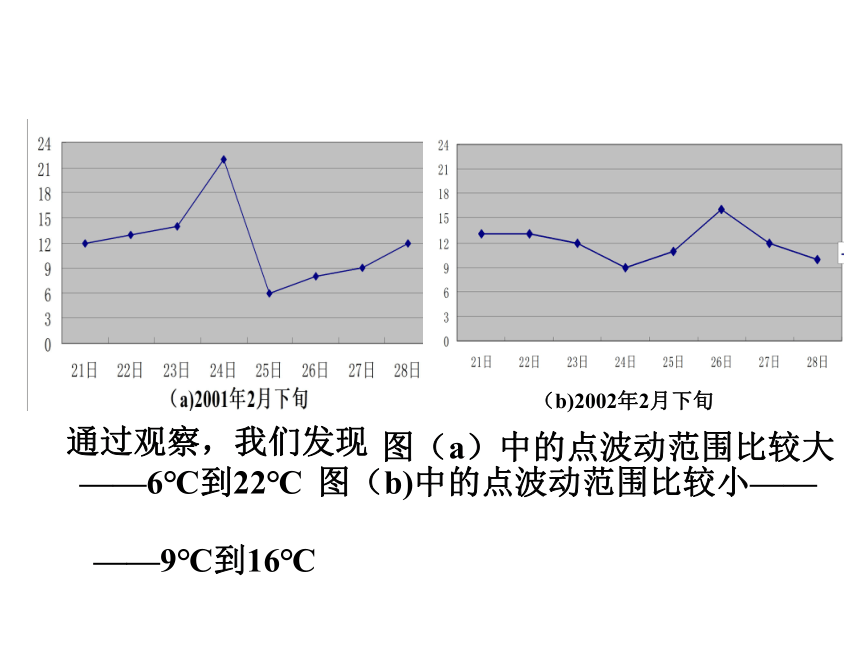
两段时间的平均气温分别是多少?表20.3.1 上海每日最高气温统计表(℃)情景创设12℃12℃这两个时段的气温情况总体上有什么差异呢?(b)2002年2月下旬通过观察,我们发现图(a)中的点波动范围比较大——6℃到22℃
图(b)中的点波动范围比较小————9℃到16℃
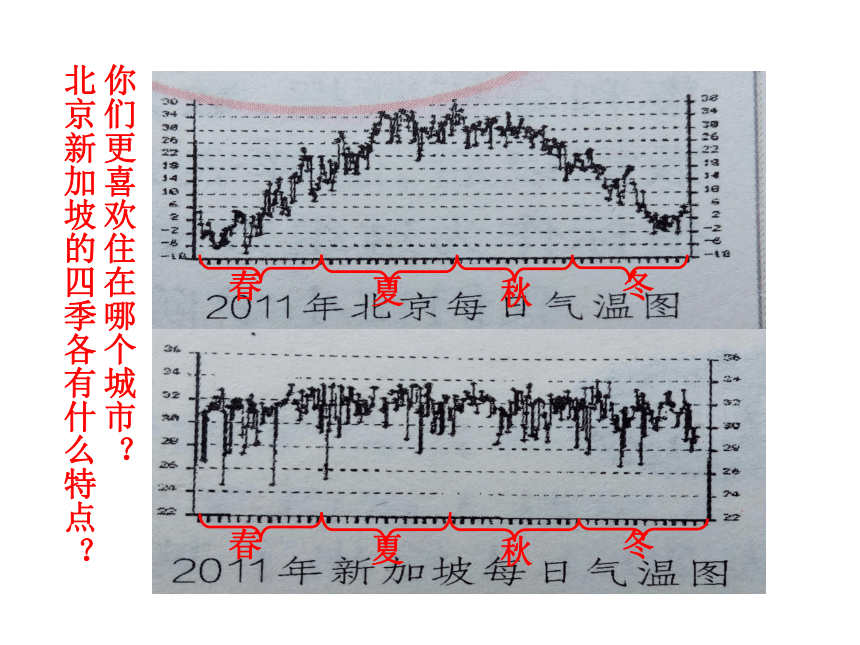
你们更喜欢住在哪个城市?
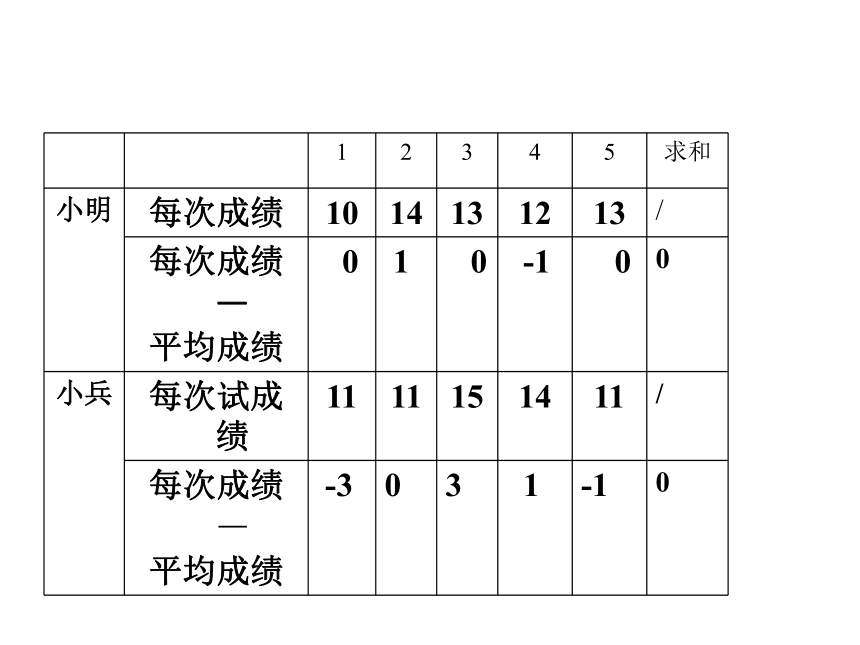
北京新加坡的四季各有什么特点?春夏秋冬春夏秋冬小明和小兵两人参加体育项目训练,近期的五次测试成绩如表21.3.2所示.谁的成绩较为稳定?为什么?
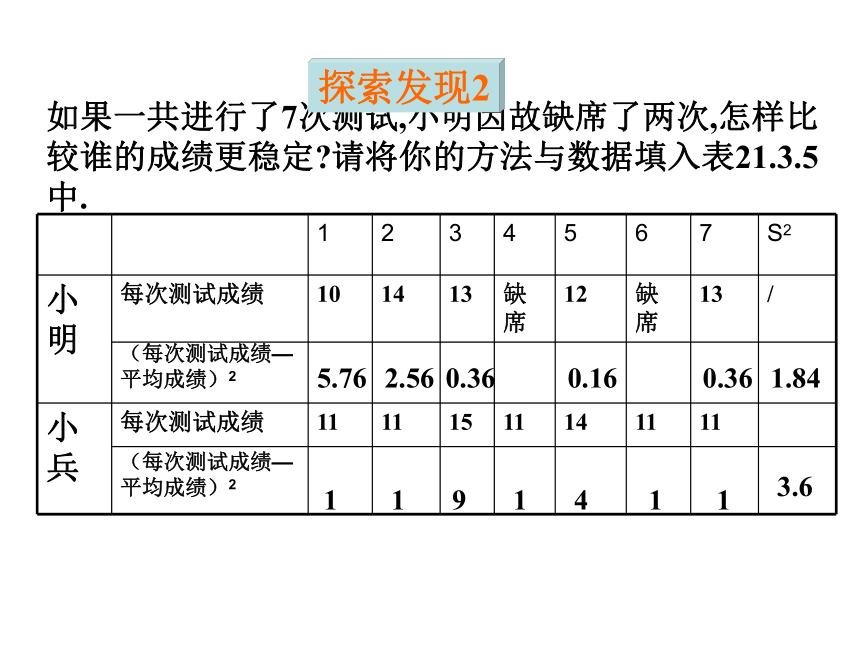
探索发现1我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差.如果一共进行了7次测试,小明因故缺席了两次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表21.3.5中.11914115.762.560.360.160.361.843.6(每次测试成绩—平均成绩)2(每次测试成绩—平均成绩)2探索发现2发现:
方差越小,离散程度越小,波动越小.
方差越大,离散程度越大,波动越大方差------ 描述一组数据的波动大小或者与平均值的离散程度的大小.总结:
平均数------反映一组数据的总体趋势方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.1.比较下列两组数据的方差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:先求平均数 A组方差: 典型例题比较下列两组数据的方差
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:求方差: A组的方差﹤B组的方差 算一算,第150页问题1中哪一年气温的离散程度较大?和你从图21.3.1中直观看出的结果一致吗?解:2001年2月下旬气温的方差为20.75(℃2),2002年2月下旬气温的方差为4( ℃2),因此2001年2月下旬气温的离散程度较大,和图中直观的结果一致。随堂练习1.某校篮球队队员中最高队员的身高是192cm,最矮队员的身高是174cm,则队员身高的极差是______.
2.甲,乙两位同学在几次数学测验中,各自的平均成绩都是88分,已知甲的方差为0.62,乙的方差为0.73,则( )
A.甲成绩比乙成绩稳定 B.乙成绩比甲成绩好 C.甲,乙成绩一样 D.甲,乙成绩无法比较
课堂检测18cmA3.在一次射击练习中,甲,乙两人前5次射击成绩分别为(单位:环)
甲:10 8 10 10 7
乙:7 10 9 9 10
则这次练习中,甲,乙两人方差S甲2与S乙2的大小关系是( )
A.S甲 2>S 乙2 B.S 甲2 C.S 甲2=S 乙2 D.无法 确定
B
4.甲,乙两人射击10次,它们的平均成绩为7环,10次射击成绩的方差分别是:
s甲2=3,s乙2=1.2,成绩较为稳定的是_______.(填“甲”或“乙”)
乙5.两台机床同时生产直径为10个单位的零件,为了检验产品的质量,质检员从两台机床的产品中各抽出5件进行测量,结果如下:
如果你是质检员,在收集到上述数据后,你将利用哪些统计知识为判断这两台机床生产的零件的质量优劣. 5.(1)由于x甲=x乙=10,因此平均直径反映不出两台机床生产出的零件的质量优劣
(2)S 甲 2=2,S 乙2=3.6,由于S 甲2 (2)方法小结:
求方差
先平均,再求差,然后平方,最后再平均
.课堂小结
两段时间的平均气温分别是多少?表20.3.1 上海每日最高气温统计表(℃)情景创设12℃12℃这两个时段的气温情况总体上有什么差异呢?(b)2002年2月下旬通过观察,我们发现图(a)中的点波动范围比较大——6℃到22℃
图(b)中的点波动范围比较小————9℃到16℃
你们更喜欢住在哪个城市?
北京新加坡的四季各有什么特点?春夏秋冬春夏秋冬小明和小兵两人参加体育项目训练,近期的五次测试成绩如表21.3.2所示.谁的成绩较为稳定?为什么?
探索发现1我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差.如果一共进行了7次测试,小明因故缺席了两次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表21.3.5中.11914115.762.560.360.160.361.843.6(每次测试成绩—平均成绩)2(每次测试成绩—平均成绩)2探索发现2发现:
方差越小,离散程度越小,波动越小.
方差越大,离散程度越大,波动越大方差------ 描述一组数据的波动大小或者与平均值的离散程度的大小.总结:
平均数------反映一组数据的总体趋势方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.1.比较下列两组数据的方差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:先求平均数 A组方差: 典型例题比较下列两组数据的方差
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:求方差: A组的方差﹤B组的方差 算一算,第150页问题1中哪一年气温的离散程度较大?和你从图21.3.1中直观看出的结果一致吗?解:2001年2月下旬气温的方差为20.75(℃2),2002年2月下旬气温的方差为4( ℃2),因此2001年2月下旬气温的离散程度较大,和图中直观的结果一致。随堂练习1.某校篮球队队员中最高队员的身高是192cm,最矮队员的身高是174cm,则队员身高的极差是______.
2.甲,乙两位同学在几次数学测验中,各自的平均成绩都是88分,已知甲的方差为0.62,乙的方差为0.73,则( )
A.甲成绩比乙成绩稳定 B.乙成绩比甲成绩好 C.甲,乙成绩一样 D.甲,乙成绩无法比较
课堂检测18cmA3.在一次射击练习中,甲,乙两人前5次射击成绩分别为(单位:环)
甲:10 8 10 10 7
乙:7 10 9 9 10
则这次练习中,甲,乙两人方差S甲2与S乙2的大小关系是( )
A.S甲 2>S 乙2 B.S 甲2
B
4.甲,乙两人射击10次,它们的平均成绩为7环,10次射击成绩的方差分别是:
s甲2=3,s乙2=1.2,成绩较为稳定的是_______.(填“甲”或“乙”)
乙5.两台机床同时生产直径为10个单位的零件,为了检验产品的质量,质检员从两台机床的产品中各抽出5件进行测量,结果如下:
如果你是质检员,在收集到上述数据后,你将利用哪些统计知识为判断这两台机床生产的零件的质量优劣. 5.(1)由于x甲=x乙=10,因此平均直径反映不出两台机床生产出的零件的质量优劣
(2)S 甲 2=2,S 乙2=3.6,由于S 甲2
求方差
先平均,再求差,然后平方,最后再平均
.课堂小结
