2018-2019学年人教版必修二 第五章 曲线运动 单元测试
文档属性
| 名称 | 2018-2019学年人教版必修二 第五章 曲线运动 单元测试 |  | |
| 格式 | zip | ||
| 文件大小 | 75.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-04-20 19:53:07 | ||
图片预览




文档简介
人教版高中物理必修2
第五章曲线运动章末复习题(一)
一、选择题(每小题4分,共32分)
1.一物体在三个共点力作用下做匀速直线运动,若突然撤去其中一个力,其余两力不变,此物体不可能做( )
A.匀加速直线运动 B.匀减速直线运动
C.类似于平抛运动 D.匀速圆周运动
2.一小船以恒定的航速渡河,当行至河中央时,水流速度突然变大,则小船渡河时间将( )
A.增大 B.减小
C.不变 D.不能确定
3.下列说法正确的是( )
A.做匀速圆周运动的物体的加速度恒定
B.做匀速圆周运动的物体所受合外力为零
C.做匀速圆周运动的物体的速度大小是不变的
D.做匀速圆周运动的物体处于平衡状态
4.如图所示,把一个长为20 cm、倔强系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 g的小球,当小球以转/分的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长应为( )
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
5.一圆盘可以绕其竖直轴在图所示水平面内转动,圆盘半径为R.甲、乙物体质量分别是M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为L(L<R)的轻绳连在一起.若将甲物体放在转轴位置上,甲、乙之间连线刚好沿半径方向被拉直,要使两物体与圆盘间不发生相对滑动,则转盘旋转角速度的最大值不得超过(两物体均看作质点) ( )
A.
B.
C.
D.
6.如图所示,小球m在竖直放置的内壁光滑的圆形细管内做圆周运动,则
①小球通过最高点的最小速度为v=
②小球通过最高点的最小速度为零
③小球通过最高点时一定受到向上的支持力
④小球通过最低点时一定受到外管壁的向上的弹力
以上说法正确的是( )
A.①② B.①③ C.②④ D.③④
7.在光滑的水平面上,一物体从静止开始,在前5 s受一个向东方向、大小为10 N的水平恒力作用,从第5 s末开始改受指向正北方向、大小为5 N的水平恒力作用10 s钟,则从物体刚运动时计时,下列说法不正确的是( )
A.物体从第5 s末开始做曲线运动
B.物体在第10 s末的加速度方向是指向正北方向
C.物体在第10 s末向正北运动
D.物体在第15 s末的速度方向是东偏北45°角
8.如图所示,小球C用两根长度相等、不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述不正确的是( )
A.角速度只有超过某一值时,细线AC才会对小球C有拉力作用
B.细线BC的拉力随角速度的增大而增大
C.不论角速度如何变化,细线BC的拉力总大于细线AC的拉力
D.当角速度增大到某一值时,总会出现细线AC的拉力大于细线BC的拉力
二、非选择题(共68分)
9.(5分)水平转盘上放一小木块,当转数为60转/分时,木块离轴8 cm,并恰好与转盘间无相对滑动;当转数增加到120转/分时,木块应放在离轴________cm处才能刚好与转盘保持相对静止.
10.(5分)第一次从高为h处水平抛出一个球,其水平射程为s,第二次用跟前一次相同的速度从另一处水平抛出另一个球,水平射程比前一次多了Δs,不计空气阻力,则第二次抛出点的高度为________.
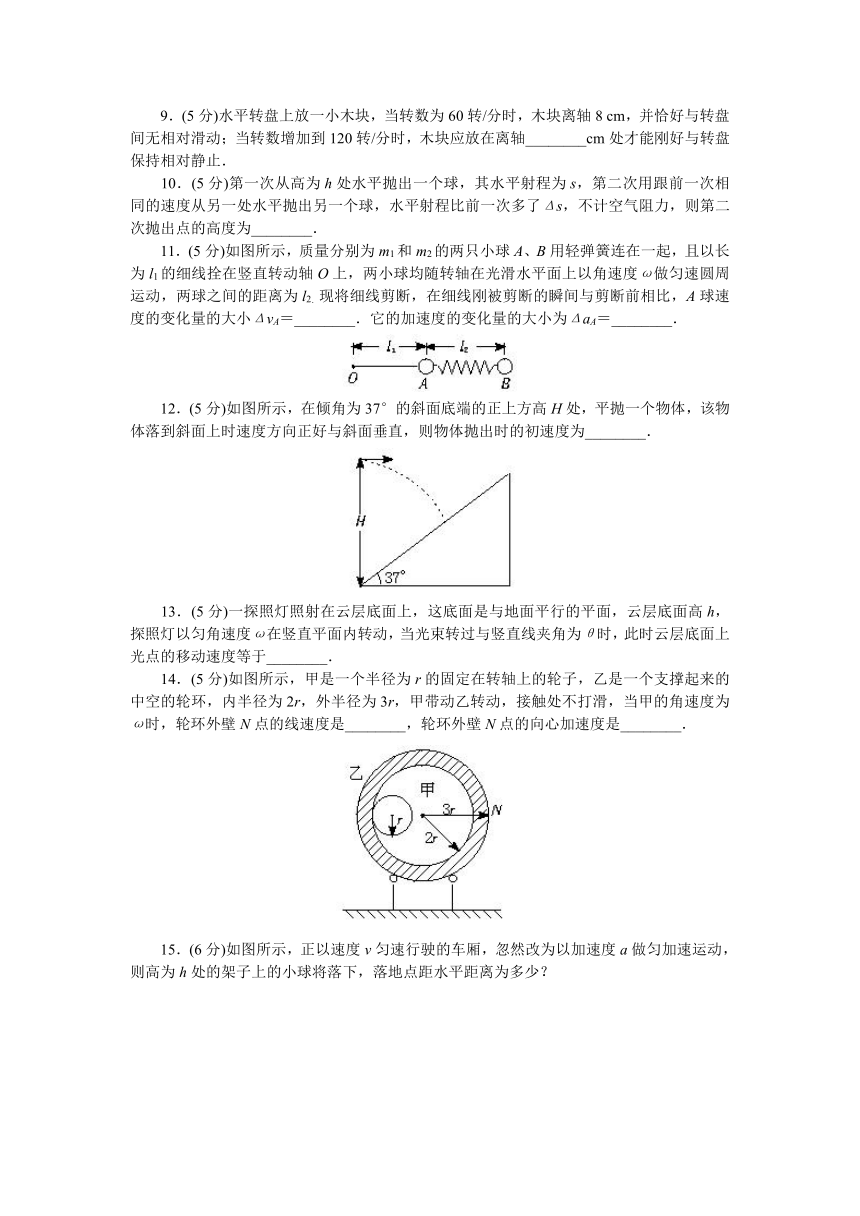
11.(5分)如图所示,质量分别为m1和m2的两只小球A、B用轻弹簧连在一起,且以长为l1的细线拴在竖直转动轴O上,两小球均随转轴在光滑水平面上以角速度ω做匀速圆周运动,两球之间的距离为l2.现将细线剪断,在细线刚被剪断的瞬间与剪断前相比,A球速度的变化量的大小ΔvA=________.它的加速度的变化量的大小为ΔaA=________.
12.(5分)如图所示,在倾角为37°的斜面底端的正上方高H处,平抛一个物体,该物体落到斜面上时速度方向正好与斜面垂直,则物体抛出时的初速度为________.
13.(5分)一探照灯照射在云层底面上,这底面是与地面平行的平面,云层底面高h,探照灯以匀角速度ω在竖直平面内转动,当光束转过与竖直线夹角为θ时,此时云层底面上光点的移动速度等于________.
14.(5分)如图所示,甲是一个半径为r的固定在转轴上的轮子,乙是一个支撑起来的中空的轮环,内半径为2r,外半径为3r,甲带动乙转动,接触处不打滑,当甲的角速度为ω时,轮环外壁N点的线速度是________,轮环外壁N点的向心加速度是________.
15.(6分)如图所示,正以速度v匀速行驶的车厢,忽然改为以加速度a做匀加速运动,则高为h处的架子上的小球将落下,落地点距水平距离为多少?
16.(6分)从高H的地方A平抛一物体,其水平射程为2s,在A点正上方高为2H的地方B点,以同方向平抛另一物体,其水平射程为s,二物在空中的运行轨道在同一竖直平面内,且都从同一屏M的顶端擦过,求屏M的高度.
17.(6分)水平抛出一个小球,t s末的速度与水平方向的夹角为θ1,(t+1)s末的速度与水平方向的夹角为θ2,求小球的初速度大小.
18.(6分)质量均为m的三个小球A、B、C分别固定在长为3L的轻质细杆上,OA=OB=BC=L,杆绕O点以角速度ω旋转,求杆上每段张力的大小.
19.(7分)如图所示,吊臂钳子夹着一块m=50 g的砖块,它们接触处的动摩擦因数为μ=0.4,绳索悬点到砖块重心的距离L=4 m,在下列两种情况下,为使砖块不滑出,钳口对砖块的压力至少多大?
(1)吊臂使砖块以4 m/s的速度匀速向右行驶.
(2)吊臂突然停止.
20.(7分)如图所示,长为l的细绳的一端系一小球,另一端悬于光滑的平面上方h高处(h<l),球在水平面上以n转/秒做匀速圆周运动时,水平面上受到的压力多大?为使球离开平面,n的最大值多大?
参考答案
一、选择题(每小题4分,共32分)
1.解析:由题知物体所受三个力的合力为零.撤去其中一个力,另两力的合力与撤去的力等值、反向,且一定是恒力.若此恒力的方向与原运动方向成夹角θ,当θ=0°时,物体做匀加速直线运动;当θ=180°时,物体做匀减速直线运动;当θ=90°时,物体做类平抛运动.故A、B、C均可能.向心力方向在变,故D不可能.
答案:D
2.C
3.C
4.解析: ΔL=m4π2n2r, (r-L0)=m4π2n2r,360(r-0.2)=0.5×4π2()2r,r=0.25m=25 cm,ΔL=(r-L0)=5 cm.
故C选项正确.
答案:C
5.解析:m物体做圆周运动的向心力由两物体受的静摩擦力提供,且随圆盘角速度增大而增大.要使两物体与转盘间不发生相对滑动,而且转盘角速度达到最大,两物体受到的静摩擦力也达到最大.即μmg+μMg=mω2L
ω=
故选项D正确.
答案:D
6.解析:小球在圆形管道中做圆周运动,受到内外管壁的双面约束,所以小球通过最高点时最小速度应为零,此时小球受重力G和竖直向上的弹力FN的作用,合力为零,在轨道最高点,当v=时,FN=0,小球只受重力,当0时,管外壁对小球产生向下的弹力FN,F合=mg+FN.因此,小球经过最高点时受力情况要据其运动速度和半径决定,但小球经过最低点时,则一定受到向上的弹力FN,F合=FN-mg向上提供向心力,本题②④正确,故选C.
答案:C
7.解析:物体在前5 s钟,做初速度为零的匀加速直线运动,从第5 s末开始受到与速度方向成90°角的恒力作用,物体开始做曲线运动,其轨迹为抛物线,故A正确,第5 s末开始作用力方向指向正北,因此第10 s末加速度方向指向正北方向,而速度方向一定不与加速度方向相同,故B正确,C错误,如果把前15 s物体的运动分解成正东和正北方向两个分运动,第5 s末物体的速度方向正东.v1==m/s,从第5 s末到第15 s末,物体向正北方向的速度达到v2= = m/s.
所以物体的合速度方向为东偏北45°角.D正确.本题答案为C.
答案:C
8.解析:当竖直杆不转动时,小球只使细线BC张紧而细线AC处于松弛状态.当竖直杆转动但不快时,BC拉着小球做圆锥摆运动即小球在水平面内做匀速圆周运动.此时小球只受到BC绳的拉力F1和重力作用,合外力提供向心力,故合外力水平,如图甲,得cosθ=
可见,ω↗,θ↗,当角速度达到某一数值ω0时,细线AC才拉直,角速度再增大,细线AC张紧对小球产生拉力作用.故A正确.
在细线AC未拉直时,细线BC的拉力
F1=mg/cosθ=mω2L 所以ω↗,拉力F1↗,
在细线AC拉直后,小球受三个力作用
如图乙,此时,F1cosα=F2cosα+mg
故F1>F2 C正确,D错.
又因为F1sinα+F2sinα=mω2Lsinα
所以解方程组得
F1= B选项正确.本题应选D.
答案:D
二、非选择题(共68分)
9.解析:F=m4π2n12r1=m4π2n22r2,r2=·r1=()2r1=r1=×8=2 cm.
答案:2
10.解析:第一次s=v0t=v0 ①
第二次(s+Δs)=v0t′=v0 ②
得:h′=(1+)2·h
答案:(1+)2·h
11.解析:细线剪断前:
球A的加速度aA=ω2l1
球B而言,F2=m2ω2(l1+l2)
细线剪断瞬间:
球A而言,F2=m1aA′,aA′=ω2(l1+l2)
故A球加速度的变化量
Δ aA=aA′-(-aA)=aA′+aA=[(m1+m2)l1+m2l2 ω2/m1
A球速度变化量ΔvA=0
答案:0;[(m1+m2)l1+m2l2 ω2/m1
12.解析:如图示,分解平抛物体的位移和末速度,设水平位移为s,末速度的竖直分速度为vy, =tan37°=
vy=v0=gt 所以t=
s=v0t=v0·=
H-s·tan37°=
H-·=(v0)2·
所以H= v0=
答案:
13.解析:云层底面上光点的移动速度为合速度,它可分解为一个沿着光束方向的分速度v2和一个垂直光束方向的分速度v1,如图示,v1=ω·R=ω· v=v1/cosθ=
答案:ωh/cos2θ
14.解析:甲、乙两轮接触处不打滑;接触处线速度相同,甲轮边缘的线速度v=ωr,则乙轮环内径2r的圆周上各点线速度也为v乙(内)=ωr,其角速度ω′===0.5ω,乙轮环上各点的角速度相等,则
N点的线速度vN=ω·3r=1.5ωr
a==0.75ω2r
答案:1.5ωr;0.75ω2r
15.解析:小球离开架子做平抛运动,t=,小球的水平位移
s1=v0t=v0,在此过程中,车厢做初速度为v的匀加速运动,
s2=v0t+at2=v0+a·
所以Δs=s2-s1=h
答案:h
16.解析:如图,设屏高为h,则A、B物体到M顶端的飞行时间分别为tA、tB,由题意:对A:2s=vA·
对B:s=vB·=vB··
两式相比:=2 s′=vA·
s′=vB· 所以h=H
答案: H
17.解析:该题应用平抛运动规律求解,由题意可知,在t秒末小球竖直方向分速度v1y=v0tanθ1,在(t+1)秒末小球竖直方向分速度v2y=v0tanθ2,由匀加速直线运动公式
v2y=v1y+g(t+1-t)
所以v0=
答案:
18.解析:设OA、AB、BC杆上的张力分别为F1、F2、F3,如图,对A、B、C小球进行受力分析,且由向心力公式,列出方程:
对A:F1-F2=mω2L
对B:F2-F3=mω2·2L
对C:F3=mω2·3L
所以解联立方程得:
F1=6mω2L F2=5mω2L F3=3mω2L
答案:6mω2L;5mω2L;3mω2L
19.解析:如图,砖块受到五个力作用:重力mg,压力F1,F2,摩擦力Ff1、Ff2
(1)砖块做匀速运动时,设钳口对砖块的压力至少为FN,由平衡条件
mg=2Ff=2μFN
所以FN===625 N
(2)吊臂突然停止时,砖块做圆周运动,设钳口对砖块的压力至少为FN′
Ff′=μFN′
因摩擦力和重力的合力为向心力
所以2Ff′-mg=m
2μFN′-mg=m
FN′===875 N
答案:(1)625 N (2)875 N
20.解析:小球受三力作用:重力mg,绳的拉力F,水平面的支持力FN,它们在竖直方向上的合力平衡,即Fcosθ+FN=mg
在水平方向的合力为小球做圆周运动的向心力,即Fsinθ=4π2n2mR R=l·sinθ
所以FN=mg-Fcosθ
=mg-4π2n2ml·
=mg-m4π2n2h
小球不离开平面的条件是 FN≥0
即mg-4π2n2mh≥0 n≤
最大转速为nmax=
答案:mg-4π2n2mh;nmax=
第五章曲线运动章末复习题(一)
一、选择题(每小题4分,共32分)
1.一物体在三个共点力作用下做匀速直线运动,若突然撤去其中一个力,其余两力不变,此物体不可能做( )
A.匀加速直线运动 B.匀减速直线运动
C.类似于平抛运动 D.匀速圆周运动
2.一小船以恒定的航速渡河,当行至河中央时,水流速度突然变大,则小船渡河时间将( )
A.增大 B.减小
C.不变 D.不能确定
3.下列说法正确的是( )
A.做匀速圆周运动的物体的加速度恒定
B.做匀速圆周运动的物体所受合外力为零
C.做匀速圆周运动的物体的速度大小是不变的
D.做匀速圆周运动的物体处于平衡状态
4.如图所示,把一个长为20 cm、倔强系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 g的小球,当小球以转/分的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长应为( )
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
5.一圆盘可以绕其竖直轴在图所示水平面内转动,圆盘半径为R.甲、乙物体质量分别是M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为L(L<R)的轻绳连在一起.若将甲物体放在转轴位置上,甲、乙之间连线刚好沿半径方向被拉直,要使两物体与圆盘间不发生相对滑动,则转盘旋转角速度的最大值不得超过(两物体均看作质点) ( )
A.
B.
C.
D.
6.如图所示,小球m在竖直放置的内壁光滑的圆形细管内做圆周运动,则
①小球通过最高点的最小速度为v=
②小球通过最高点的最小速度为零
③小球通过最高点时一定受到向上的支持力
④小球通过最低点时一定受到外管壁的向上的弹力
以上说法正确的是( )
A.①② B.①③ C.②④ D.③④
7.在光滑的水平面上,一物体从静止开始,在前5 s受一个向东方向、大小为10 N的水平恒力作用,从第5 s末开始改受指向正北方向、大小为5 N的水平恒力作用10 s钟,则从物体刚运动时计时,下列说法不正确的是( )
A.物体从第5 s末开始做曲线运动
B.物体在第10 s末的加速度方向是指向正北方向
C.物体在第10 s末向正北运动
D.物体在第15 s末的速度方向是东偏北45°角
8.如图所示,小球C用两根长度相等、不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述不正确的是( )
A.角速度只有超过某一值时,细线AC才会对小球C有拉力作用
B.细线BC的拉力随角速度的增大而增大
C.不论角速度如何变化,细线BC的拉力总大于细线AC的拉力
D.当角速度增大到某一值时,总会出现细线AC的拉力大于细线BC的拉力
二、非选择题(共68分)
9.(5分)水平转盘上放一小木块,当转数为60转/分时,木块离轴8 cm,并恰好与转盘间无相对滑动;当转数增加到120转/分时,木块应放在离轴________cm处才能刚好与转盘保持相对静止.
10.(5分)第一次从高为h处水平抛出一个球,其水平射程为s,第二次用跟前一次相同的速度从另一处水平抛出另一个球,水平射程比前一次多了Δs,不计空气阻力,则第二次抛出点的高度为________.
11.(5分)如图所示,质量分别为m1和m2的两只小球A、B用轻弹簧连在一起,且以长为l1的细线拴在竖直转动轴O上,两小球均随转轴在光滑水平面上以角速度ω做匀速圆周运动,两球之间的距离为l2.现将细线剪断,在细线刚被剪断的瞬间与剪断前相比,A球速度的变化量的大小ΔvA=________.它的加速度的变化量的大小为ΔaA=________.
12.(5分)如图所示,在倾角为37°的斜面底端的正上方高H处,平抛一个物体,该物体落到斜面上时速度方向正好与斜面垂直,则物体抛出时的初速度为________.
13.(5分)一探照灯照射在云层底面上,这底面是与地面平行的平面,云层底面高h,探照灯以匀角速度ω在竖直平面内转动,当光束转过与竖直线夹角为θ时,此时云层底面上光点的移动速度等于________.
14.(5分)如图所示,甲是一个半径为r的固定在转轴上的轮子,乙是一个支撑起来的中空的轮环,内半径为2r,外半径为3r,甲带动乙转动,接触处不打滑,当甲的角速度为ω时,轮环外壁N点的线速度是________,轮环外壁N点的向心加速度是________.
15.(6分)如图所示,正以速度v匀速行驶的车厢,忽然改为以加速度a做匀加速运动,则高为h处的架子上的小球将落下,落地点距水平距离为多少?
16.(6分)从高H的地方A平抛一物体,其水平射程为2s,在A点正上方高为2H的地方B点,以同方向平抛另一物体,其水平射程为s,二物在空中的运行轨道在同一竖直平面内,且都从同一屏M的顶端擦过,求屏M的高度.
17.(6分)水平抛出一个小球,t s末的速度与水平方向的夹角为θ1,(t+1)s末的速度与水平方向的夹角为θ2,求小球的初速度大小.
18.(6分)质量均为m的三个小球A、B、C分别固定在长为3L的轻质细杆上,OA=OB=BC=L,杆绕O点以角速度ω旋转,求杆上每段张力的大小.
19.(7分)如图所示,吊臂钳子夹着一块m=50 g的砖块,它们接触处的动摩擦因数为μ=0.4,绳索悬点到砖块重心的距离L=4 m,在下列两种情况下,为使砖块不滑出,钳口对砖块的压力至少多大?
(1)吊臂使砖块以4 m/s的速度匀速向右行驶.
(2)吊臂突然停止.
20.(7分)如图所示,长为l的细绳的一端系一小球,另一端悬于光滑的平面上方h高处(h<l),球在水平面上以n转/秒做匀速圆周运动时,水平面上受到的压力多大?为使球离开平面,n的最大值多大?
参考答案
一、选择题(每小题4分,共32分)
1.解析:由题知物体所受三个力的合力为零.撤去其中一个力,另两力的合力与撤去的力等值、反向,且一定是恒力.若此恒力的方向与原运动方向成夹角θ,当θ=0°时,物体做匀加速直线运动;当θ=180°时,物体做匀减速直线运动;当θ=90°时,物体做类平抛运动.故A、B、C均可能.向心力方向在变,故D不可能.
答案:D
2.C
3.C
4.解析: ΔL=m4π2n2r, (r-L0)=m4π2n2r,360(r-0.2)=0.5×4π2()2r,r=0.25m=25 cm,ΔL=(r-L0)=5 cm.
故C选项正确.
答案:C
5.解析:m物体做圆周运动的向心力由两物体受的静摩擦力提供,且随圆盘角速度增大而增大.要使两物体与转盘间不发生相对滑动,而且转盘角速度达到最大,两物体受到的静摩擦力也达到最大.即μmg+μMg=mω2L
ω=
故选项D正确.
答案:D
6.解析:小球在圆形管道中做圆周运动,受到内外管壁的双面约束,所以小球通过最高点时最小速度应为零,此时小球受重力G和竖直向上的弹力FN的作用,合力为零,在轨道最高点,当v=时,FN=0,小球只受重力,当0
答案:C
7.解析:物体在前5 s钟,做初速度为零的匀加速直线运动,从第5 s末开始受到与速度方向成90°角的恒力作用,物体开始做曲线运动,其轨迹为抛物线,故A正确,第5 s末开始作用力方向指向正北,因此第10 s末加速度方向指向正北方向,而速度方向一定不与加速度方向相同,故B正确,C错误,如果把前15 s物体的运动分解成正东和正北方向两个分运动,第5 s末物体的速度方向正东.v1==m/s,从第5 s末到第15 s末,物体向正北方向的速度达到v2= = m/s.
所以物体的合速度方向为东偏北45°角.D正确.本题答案为C.
答案:C
8.解析:当竖直杆不转动时,小球只使细线BC张紧而细线AC处于松弛状态.当竖直杆转动但不快时,BC拉着小球做圆锥摆运动即小球在水平面内做匀速圆周运动.此时小球只受到BC绳的拉力F1和重力作用,合外力提供向心力,故合外力水平,如图甲,得cosθ=
可见,ω↗,θ↗,当角速度达到某一数值ω0时,细线AC才拉直,角速度再增大,细线AC张紧对小球产生拉力作用.故A正确.
在细线AC未拉直时,细线BC的拉力
F1=mg/cosθ=mω2L 所以ω↗,拉力F1↗,
在细线AC拉直后,小球受三个力作用
如图乙,此时,F1cosα=F2cosα+mg
故F1>F2 C正确,D错.
又因为F1sinα+F2sinα=mω2Lsinα
所以解方程组得
F1= B选项正确.本题应选D.
答案:D
二、非选择题(共68分)
9.解析:F=m4π2n12r1=m4π2n22r2,r2=·r1=()2r1=r1=×8=2 cm.
答案:2
10.解析:第一次s=v0t=v0 ①
第二次(s+Δs)=v0t′=v0 ②
得:h′=(1+)2·h
答案:(1+)2·h
11.解析:细线剪断前:
球A的加速度aA=ω2l1
球B而言,F2=m2ω2(l1+l2)
细线剪断瞬间:
球A而言,F2=m1aA′,aA′=ω2(l1+l2)
故A球加速度的变化量
Δ aA=aA′-(-aA)=aA′+aA=[(m1+m2)l1+m2l2 ω2/m1
A球速度变化量ΔvA=0
答案:0;[(m1+m2)l1+m2l2 ω2/m1
12.解析:如图示,分解平抛物体的位移和末速度,设水平位移为s,末速度的竖直分速度为vy, =tan37°=
vy=v0=gt 所以t=
s=v0t=v0·=
H-s·tan37°=
H-·=(v0)2·
所以H= v0=
答案:
13.解析:云层底面上光点的移动速度为合速度,它可分解为一个沿着光束方向的分速度v2和一个垂直光束方向的分速度v1,如图示,v1=ω·R=ω· v=v1/cosθ=
答案:ωh/cos2θ
14.解析:甲、乙两轮接触处不打滑;接触处线速度相同,甲轮边缘的线速度v=ωr,则乙轮环内径2r的圆周上各点线速度也为v乙(内)=ωr,其角速度ω′===0.5ω,乙轮环上各点的角速度相等,则
N点的线速度vN=ω·3r=1.5ωr
a==0.75ω2r
答案:1.5ωr;0.75ω2r
15.解析:小球离开架子做平抛运动,t=,小球的水平位移
s1=v0t=v0,在此过程中,车厢做初速度为v的匀加速运动,
s2=v0t+at2=v0+a·
所以Δs=s2-s1=h
答案:h
16.解析:如图,设屏高为h,则A、B物体到M顶端的飞行时间分别为tA、tB,由题意:对A:2s=vA·
对B:s=vB·=vB··
两式相比:=2 s′=vA·
s′=vB· 所以h=H
答案: H
17.解析:该题应用平抛运动规律求解,由题意可知,在t秒末小球竖直方向分速度v1y=v0tanθ1,在(t+1)秒末小球竖直方向分速度v2y=v0tanθ2,由匀加速直线运动公式
v2y=v1y+g(t+1-t)
所以v0=
答案:
18.解析:设OA、AB、BC杆上的张力分别为F1、F2、F3,如图,对A、B、C小球进行受力分析,且由向心力公式,列出方程:
对A:F1-F2=mω2L
对B:F2-F3=mω2·2L
对C:F3=mω2·3L
所以解联立方程得:
F1=6mω2L F2=5mω2L F3=3mω2L
答案:6mω2L;5mω2L;3mω2L
19.解析:如图,砖块受到五个力作用:重力mg,压力F1,F2,摩擦力Ff1、Ff2
(1)砖块做匀速运动时,设钳口对砖块的压力至少为FN,由平衡条件
mg=2Ff=2μFN
所以FN===625 N
(2)吊臂突然停止时,砖块做圆周运动,设钳口对砖块的压力至少为FN′
Ff′=μFN′
因摩擦力和重力的合力为向心力
所以2Ff′-mg=m
2μFN′-mg=m
FN′===875 N
答案:(1)625 N (2)875 N
20.解析:小球受三力作用:重力mg,绳的拉力F,水平面的支持力FN,它们在竖直方向上的合力平衡,即Fcosθ+FN=mg
在水平方向的合力为小球做圆周运动的向心力,即Fsinθ=4π2n2mR R=l·sinθ
所以FN=mg-Fcosθ
=mg-4π2n2ml·
=mg-m4π2n2h
小球不离开平面的条件是 FN≥0
即mg-4π2n2mh≥0 n≤
最大转速为nmax=
答案:mg-4π2n2mh;nmax=
