人教版数学八下18.1.2平行四边形的判定(2)课件(32张PPT)
文档属性
| 名称 | 人教版数学八下18.1.2平行四边形的判定(2)课件(32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 822.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 07:58:16 | ||
图片预览









文档简介
18.1.2平行四边形的判定
有两组对边分别平行的四边形
叫做
平行四边形
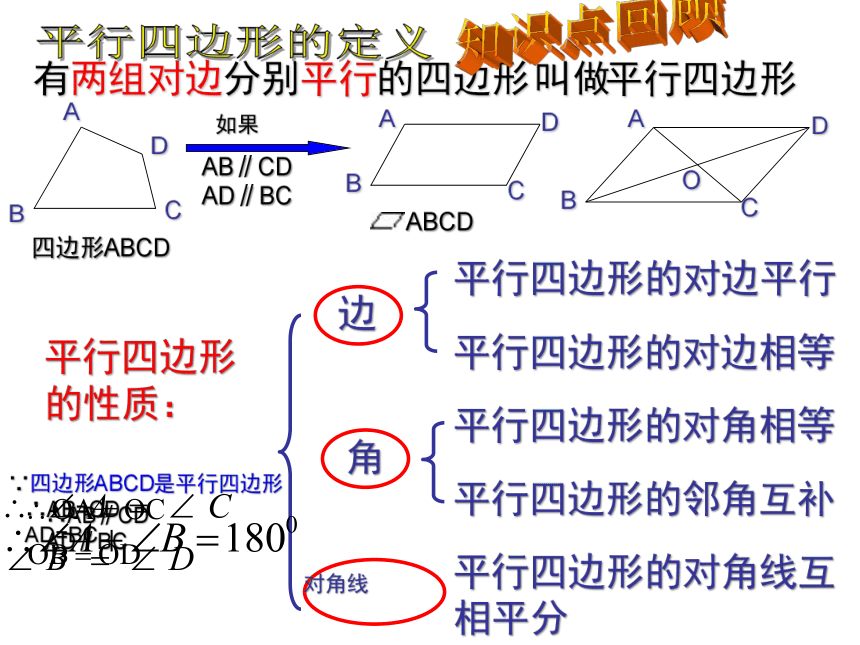
平行四边形的定义
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
知识点回顾
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
知识点回顾
平行四边形的判别方法
我们知道两组对边分别平行或相等的四边形是平行四边形,如果只考虑一组对边,它们要满足什么条件时,这个四边形才能成为平行四边形?
思考
学习目标
1.掌握用一组对边平行且相等来判定平行四边形的方法.
2.会综合运用平行四边形的各种判定方法和性质来进行推理或计算.
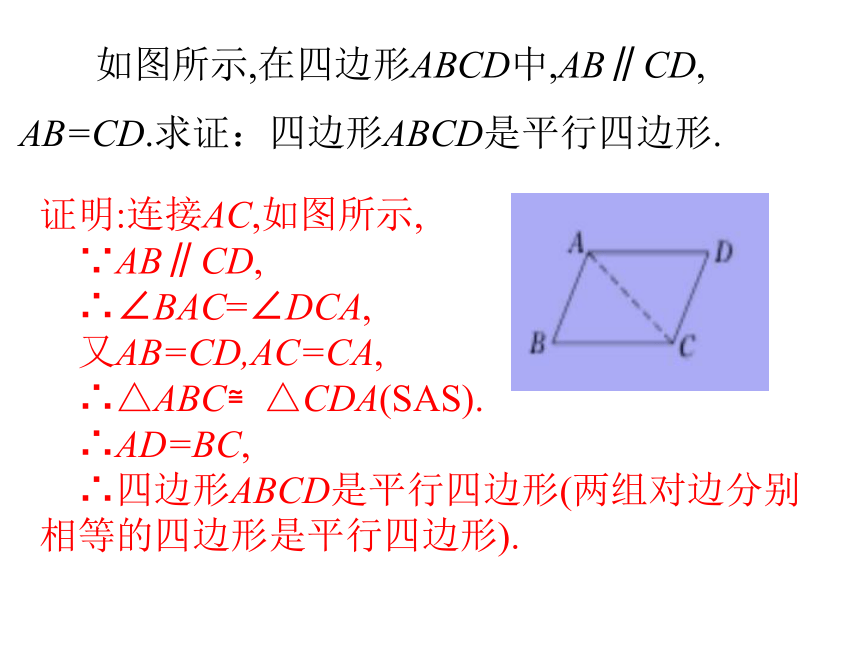
如图所示,在四边形ABCD中,AB∥CD,
AB=CD.求证:四边形ABCD是平行四边形.
证明:连接AC,如图所示,
∵AB∥CD,
∴∠BAC=∠DCA,
又AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴AD=BC,
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
用符号语言表述为:
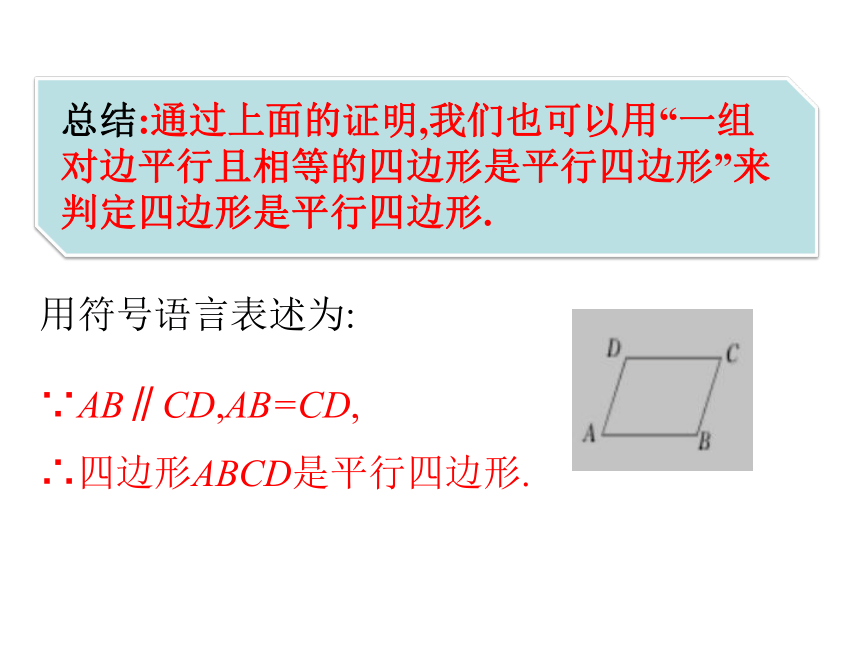
总结:通过上面的证明,我们也可以用“一组对边平行且相等的四边形是平行四边形”来判定四边形是平行四边形.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
知识拓展
90909vvv的v行四边形.
(2)一组对边相等,一组对角相等的四边形不一定是平行四边形.
例:(教材例4)如图所示,在□ABCD中,E,F分别是AB, CD的
点. 求证:四边形EBFD是平行四边形.
〔解析〕由已知条件可知:CD∥AB,AB=CD,因为E,F分别是AB,CD的中点,所以2BE= AB,2DF=CD,可得BE=DF,根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,即可证明四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB∥FD.
又 2EB=AB,2FD=CD,
∴EB=FD.
∴四边形EBFD是平行四边形.
[解题策略] 平行四边形知识的运用包括三个方面:一是直接运用平行四边形的性质去解决某些问题.例如求角的度数,线段的长度,证明角相等或线段相等等;二是判定一个四边形是平行四边形,从而判定直线平行等;三是先判定一个四边形是平行四边形,然后再用平行四边形的性质去解决某些问题.
课堂小结
平行四边形的判定方法?
从边看:
①两组对边分别平行的四边形是平行四边形.
②两组对边分别相等的四边形是平行四边形.
③一组对边平行且相等的四边形是平行四边形.
从对角线看:
对角线互相平分的四边形是平行四边形.
从角看:
两组对角分别相等的四边形是平行四边形.
检测反馈
1.四边形ABCD中,对角线AC和BD交于点O,下列条件中不能判定四边形ABCD是平行四边形的是 ( )
A.OA=OC,OB=OD B.AD∥BC,AB∥DC
C.AB=DC,AD=BC D.AB∥DC,AD=BC
解析: A为对角线互相平分,B为两组对边分别平行,C为两组对边分别相等,都能判定四边形为平行四边形,D为一组对边相等,另一组对边平行,此四边形不一定是平行四边形.故选D.
D
检测反馈
2.如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF//BE,四边形ABCD是平行四边形吗?
3.(2015·遂宁中考)如图所示,在□ABCD中,点E,F在对角线BD上,且BE=DF.求证:(1)AE=CF; (2)四边形AECF是平行四边形.
证明:(1)在□ ABCD中,AB∥CD,
AB=CD,所以∠ABE=∠CDF,
因为BE=DF,所以△ABE≌△CDF(SAS),
所以AE=CF.
(2)四边形AECF是平行四边形.
(2)由(1)中△ABE≌△CDF,
可得AE=CF,∠AEB=∠DFC,
所以∠AED=∠CFB,
所以AE∥CF,
所以四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形).
如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
巩固练习
A
B
C
D
E
F
M
N
自学课本P.47倒数两段,解答下列问题。
1、 叫做三角形的中位线,一个三角形有 条中位线。
2.在练习本上画出一个三角形,并画出它的一条中位线。
连接三角形两边中点的线段
三
自主学习
三角形的中位线有什么性质?
如图,DE是△ABC 的一条中位线.
(1)量一量DE,BC的长是多少?你能作出什么猜测?
(2)观察图形中的DE与BC,猜测DE 与BC 位置关系吗?几何画板验证一下
探究与思考
C
A
B
D
E
怎样将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
(1)剪一个三角形,记为△ABC;
(2)沿中位线DE将△ABC剪成两部分,并将△ADE绕点E顺时针旋转180°得四边形BCFD.
A
B
C
D
E
F
四边形BCFD是平行四边形吗? 为什么?
四边形BCFD是平行四边形
D
E
B
C
A
F
A
B
C
D
E
F
∵DE=EF ∠1=∠2 AE=EC
∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB
∴BD∥ CF且 BD =CF
∴四边形BCFD是平行四边形
还有另外的证法吗?
∴DF∥BC,DF=BC
又∵
即DE∥BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。
1
2
A
B
C
E
D
F
证明:如图,延长DE至F,
使EF=DE,
连接CD、AF、CF
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形∴AD FC
又D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形?
∴DE// BC 且DE=EF=1/2BC
C
E
D
F
B
A
证法三:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
数量关系
位置关系
(1)证明平行
(2)证明一条线段是另一条线
段的2倍或
A
B
C
D
E
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
三角形的中位线定理的主要用途:
第三边
巩固新知
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———
60°
4
A
B
C
D
E
D
8cm
6cm
平行于
等于 一半
4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = .
A
M
B
C
N
61°
24
5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .
A
D
B
C
E
5㎝
6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
A
B
C
D
E
F
5.2
7、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。
12
E
F
B
A
C
D
A
B
C
D
E
F
G
H
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
证明:连结AC
∵ AE=EB、CF=FB,
(三角形中位线定理)
∴EF∥AC,EF= AC
∴四边形EFGH是平行四边形
同理: HG∥AC,HG= AC
∴EF ∥HG,且EF=HG
挑战自我
知识总结:
1。判定定理:一组对边平行且相等的四边形是平行四边形
2.定义 :连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
数学思想:转化思想
1.把四边形的问题转化为三角形问题解决
2.线段的倍分问题可转化为相等问题来解决.
数学方法:在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法
本节课你有哪些收获?
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
再 见
