18.2.2菱形的性质课件 (共50张PPT)
文档属性
| 名称 | 18.2.2菱形的性质课件 (共50张PPT) | 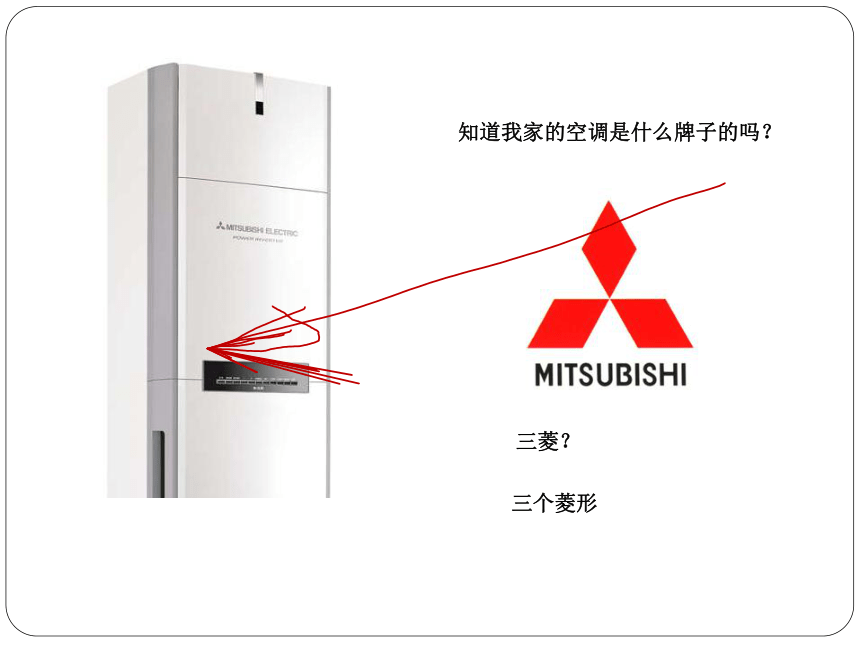 | |
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 08:54:19 | ||
图片预览








文档简介
知道我家的空调是什么牌子的吗?
三菱?
三个菱形
18.2.2 菱形的性质
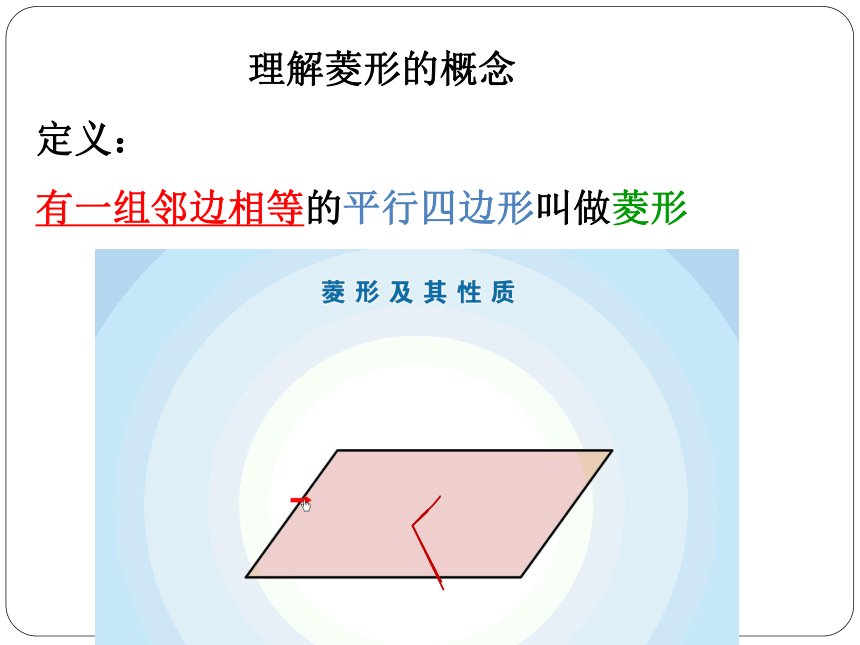
理解菱形的概念
定义:
_______________的平行四边形叫做菱形
理解菱形的概念
定义:
有一组邻边相等的平行四边形叫做菱形
茵宝
一汽丰田自主品牌——朗世
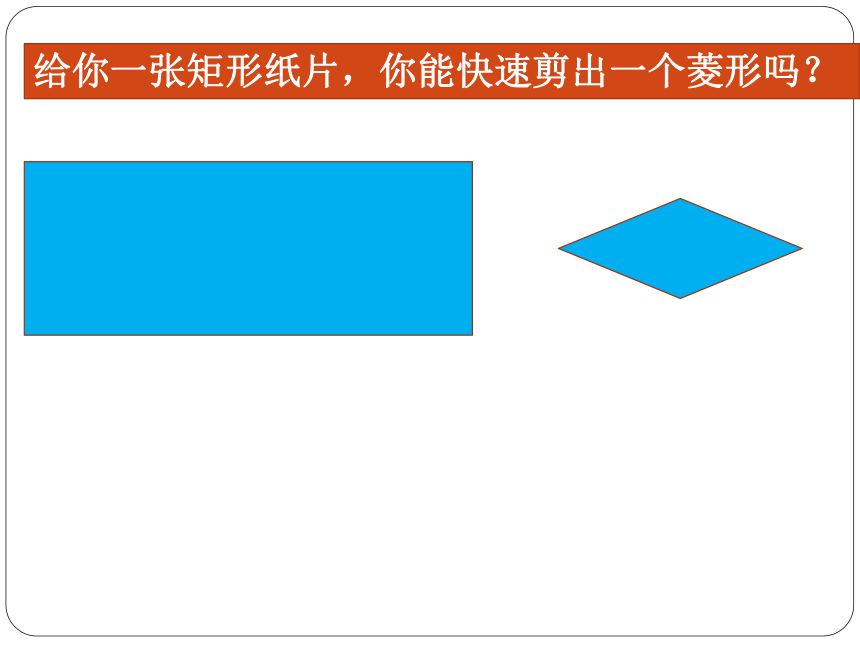
给你一张矩形纸片,你能快速剪出一个菱形吗?
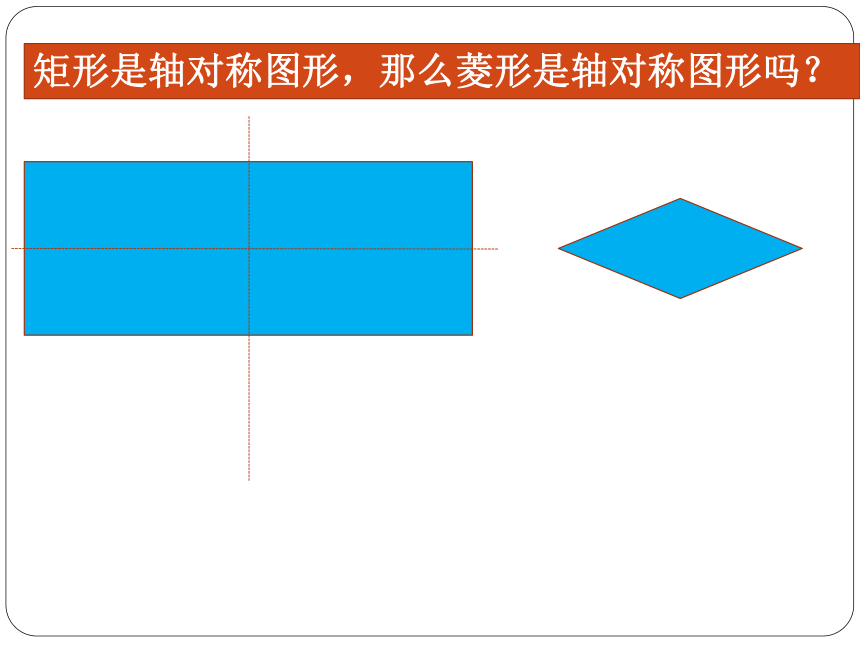
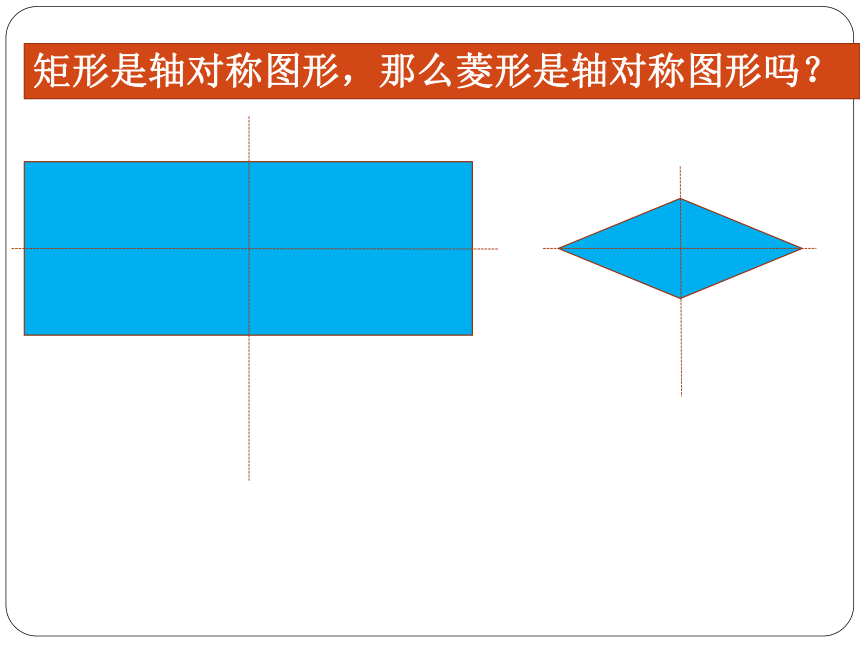
矩形是轴对称图形,那么菱形是轴对称图形吗?
矩形是轴对称图形,那么菱形是轴对称图形吗?
菱形的四条边
菱形的对角线
并且每一条对角线
菱形的性质定理
小组讨论,分享预习检测项目成果
7.如图,菱形花坛ABCD的边长为20 m,∠ABC =60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路AC、BD的长和菱形花坛ABCD的面积.
巩固练习——分层训练(15分钟)
A组:1、3
B组:3、4、5
C组:3、4、5、6
3. 在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AO=4,求AC和BD的长。
3. 在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AO=4,求AC和BD的长。
学习目标
理解菱形的概念:会区分菱形与矩形的区别,菱形与平行四边形的区别与联系。
探索并证明菱形的性质:会用菱形的对边、对角、对角线的性质进行基本的计算或证明。
在探索与证明菱形性质的过程中发展逻辑推理能力:会类比平行四边形、矩形性质研究中贯穿的观察、度量、实验、猜想、证明几个步骤进行对菱形性质的研究。
掌握解决几何问题的思路分析与思维方法:会从题设或结论出发寻求论证的思路,体会数学转化的思想。
分层检测
A组:1、2、3
B组:1、2、3、4
C组:3、4、5、6
拓展延伸
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
猜想证明 形成性质
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问
题;
2.经历类比矩形探究菱形性质的过程,通过观察、
类比、猜想、证明等活动,体会几何图形研究的
一般步骤和方法.
学习重点:
菱形性质的探索、证明和应用.
课件说明
创设情境 引出课题
问题1 我们已经学习了特殊的平行四边形——矩
形,它是从哪个角度特殊化来进行研究的?它有哪些
性质?
创设情境 引出课题
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
创设情境 引出课题
问题2 平行四边形的角特殊化得到特殊的平行四
边形——矩形;平行四边形的边特殊化,我们得到的特
殊的平行四边形是什么,它有什么特征?
创设情境 引出课题
菱形:一组邻边相等的平行四边形叫做菱形.
你能举出生活中的菱形的实际例子吗?
追问:你能画出一个菱形吗?
猜想证明 形成性质
问题3 菱形是特殊的平行四边形,因此它具有平
行四边形的所有性质.类似于矩形,菱形是否也具有一
般平行四边形不具有的特殊性质?如果有,是什么?
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
猜想证明 形成性质
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
猜想证明 形成性质
问题4 你能证明上述猜想吗?
菱形的四条边相等;对角线互相垂直,且每一条对
角线平分一组对角.
猜想证明 形成性质
问题5 现在,我们得到了菱形的性质.如果把矩形
和菱形的性质进行比较,发现它们很相似.你能写出矩
形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
运用性质 解决问题
变式 若E是BD上任意一点,那么AE与CE 有怎样
的数量关系?
例1 如图,在菱形ABCD中,若∠ABC=2∠BAD,
则∠BAD= ,△ABD为 三角形.
运用性质 解决问题
例2 如图,菱形花坛ABCD的边长为20 m,∠ABC
=60°,沿着菱形的对角线修建了两条小路AC和BD.求
两条小路的长(结果保留小数点后两位)和花坛的面积
(结果保留小数点后一位).
(1)什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所
具有的?哪些是一般平行四边形不具有的?菱
形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的
体会.
课堂小结
课后作业
作业: 教科书第57页练习1,2;
教科书第60页习题18.2第5,7题.
三菱?
三个菱形
18.2.2 菱形的性质
理解菱形的概念
定义:
_______________的平行四边形叫做菱形
理解菱形的概念
定义:
有一组邻边相等的平行四边形叫做菱形
茵宝
一汽丰田自主品牌——朗世
给你一张矩形纸片,你能快速剪出一个菱形吗?
矩形是轴对称图形,那么菱形是轴对称图形吗?
矩形是轴对称图形,那么菱形是轴对称图形吗?
菱形的四条边
菱形的对角线
并且每一条对角线
菱形的性质定理
小组讨论,分享预习检测项目成果
7.如图,菱形花坛ABCD的边长为20 m,∠ABC =60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路AC、BD的长和菱形花坛ABCD的面积.
巩固练习——分层训练(15分钟)
A组:1、3
B组:3、4、5
C组:3、4、5、6
3. 在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AO=4,求AC和BD的长。
3. 在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AO=4,求AC和BD的长。
学习目标
理解菱形的概念:会区分菱形与矩形的区别,菱形与平行四边形的区别与联系。
探索并证明菱形的性质:会用菱形的对边、对角、对角线的性质进行基本的计算或证明。
在探索与证明菱形性质的过程中发展逻辑推理能力:会类比平行四边形、矩形性质研究中贯穿的观察、度量、实验、猜想、证明几个步骤进行对菱形性质的研究。
掌握解决几何问题的思路分析与思维方法:会从题设或结论出发寻求论证的思路,体会数学转化的思想。
分层检测
A组:1、2、3
B组:1、2、3、4
C组:3、4、5、6
拓展延伸
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
猜想证明 形成性质
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问
题;
2.经历类比矩形探究菱形性质的过程,通过观察、
类比、猜想、证明等活动,体会几何图形研究的
一般步骤和方法.
学习重点:
菱形性质的探索、证明和应用.
课件说明
创设情境 引出课题
问题1 我们已经学习了特殊的平行四边形——矩
形,它是从哪个角度特殊化来进行研究的?它有哪些
性质?
创设情境 引出课题
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
创设情境 引出课题
问题2 平行四边形的角特殊化得到特殊的平行四
边形——矩形;平行四边形的边特殊化,我们得到的特
殊的平行四边形是什么,它有什么特征?
创设情境 引出课题
菱形:一组邻边相等的平行四边形叫做菱形.
你能举出生活中的菱形的实际例子吗?
追问:你能画出一个菱形吗?
猜想证明 形成性质
问题3 菱形是特殊的平行四边形,因此它具有平
行四边形的所有性质.类似于矩形,菱形是否也具有一
般平行四边形不具有的特殊性质?如果有,是什么?
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
猜想证明 形成性质
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
猜想证明 形成性质
问题4 你能证明上述猜想吗?
菱形的四条边相等;对角线互相垂直,且每一条对
角线平分一组对角.
猜想证明 形成性质
问题5 现在,我们得到了菱形的性质.如果把矩形
和菱形的性质进行比较,发现它们很相似.你能写出矩
形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
运用性质 解决问题
变式 若E是BD上任意一点,那么AE与CE 有怎样
的数量关系?
例1 如图,在菱形ABCD中,若∠ABC=2∠BAD,
则∠BAD= ,△ABD为 三角形.
运用性质 解决问题
例2 如图,菱形花坛ABCD的边长为20 m,∠ABC
=60°,沿着菱形的对角线修建了两条小路AC和BD.求
两条小路的长(结果保留小数点后两位)和花坛的面积
(结果保留小数点后一位).
(1)什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所
具有的?哪些是一般平行四边形不具有的?菱
形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的
体会.
课堂小结
课后作业
作业: 教科书第57页练习1,2;
教科书第60页习题18.2第5,7题.
