冀教版数学九下29.2 直线与圆的位置关系教学课件(共32张PPT)
文档属性
| 名称 | 冀教版数学九下29.2 直线与圆的位置关系教学课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 477.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 21:36:58 | ||
图片预览






文档简介
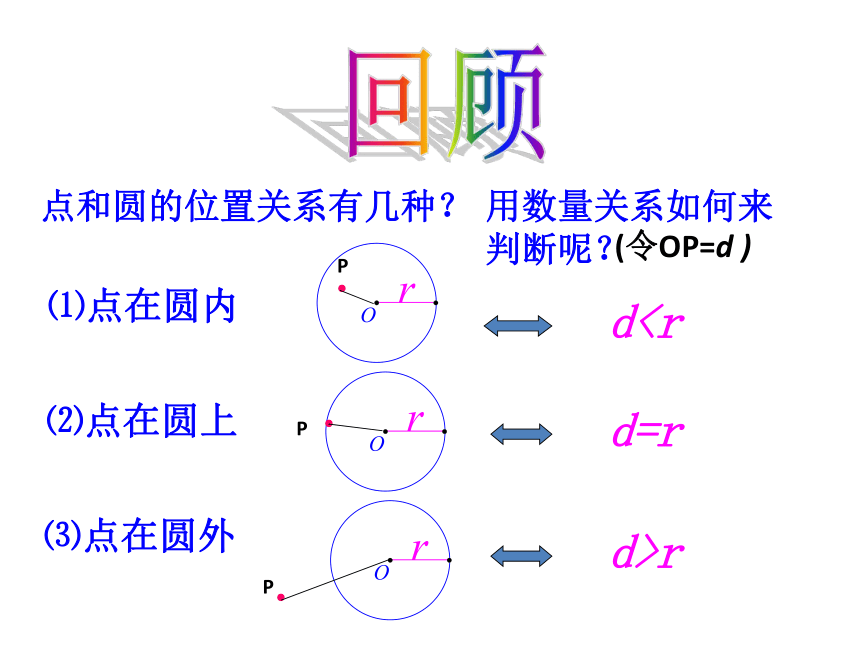
课件32张PPT。直线与圆的位置关系1、点与圆有几种位置关系?.A.A.A.A.A . B.A.A.C.A.A2、过两点能画多少个圆?它们的圆心有什么规律?过三点一定能画一个圆吗?点和圆的位置关系有几种?dr用数量关系如何来
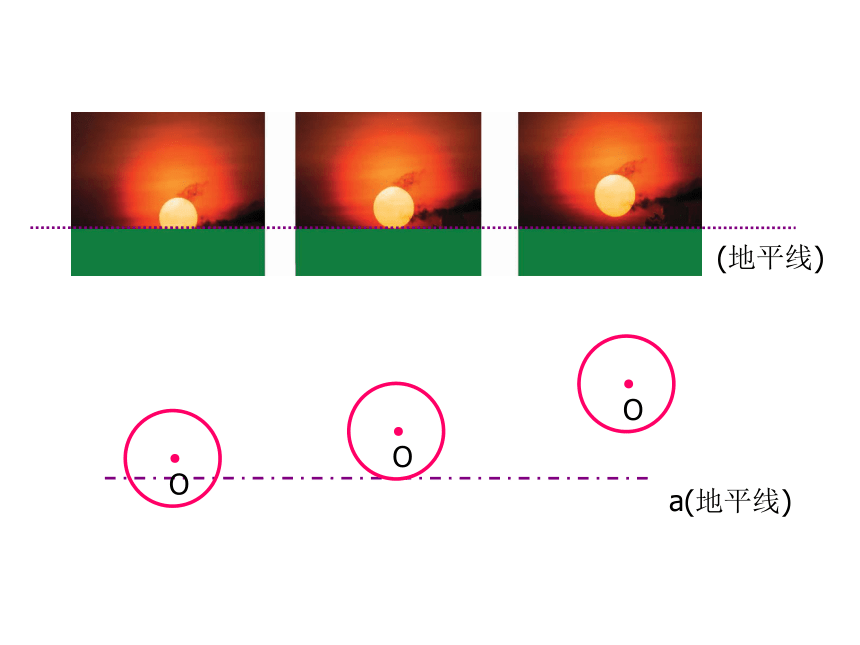
判断呢?回顾(令OP=d )想一想 你认为直线与圆有哪些位置关系?大家看日出时,在太阳升起过程中,太阳与地平线有什么关系?(地平线)a(地平线)图 1b.A.O图 2c.
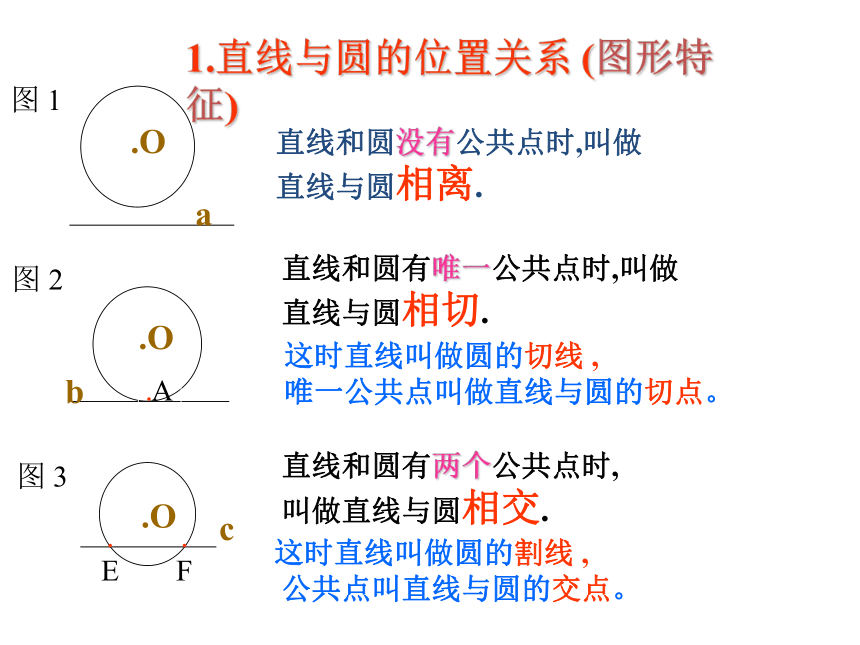
F.E.O图 3这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。直线和圆没有公共点时,叫做直线与圆相离.直线和圆有唯一公共点时,叫做直线与圆相切.直线和圆有两个公共点时,叫做直线与圆相交. 这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。1.直线与圆的位置关系 (图形特征)练习1 1、直线与圆最多有两个公共点 。… ( ) √×3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
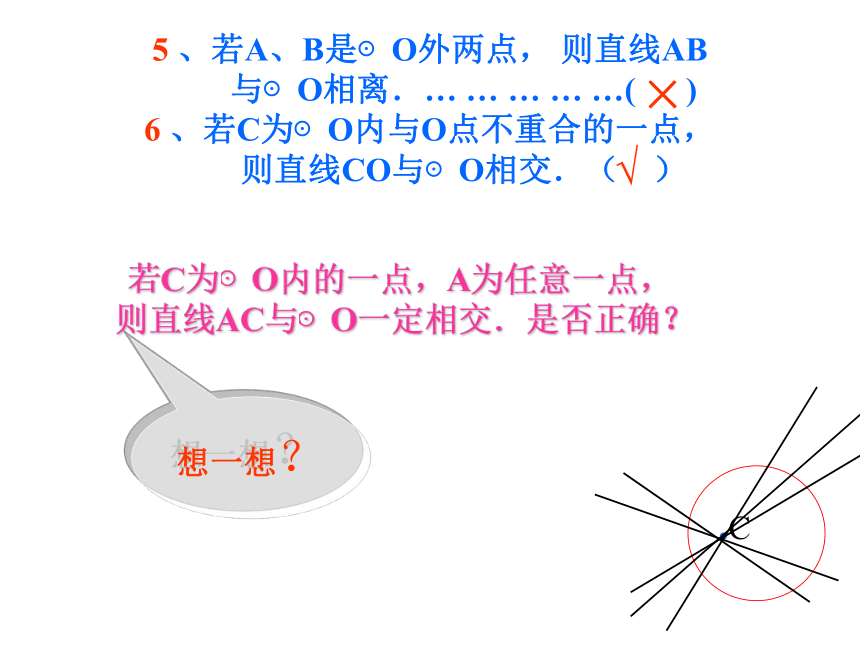
⊙O 相交或相离。………( )××.C5 、若A、B是⊙O外两点, 则直线AB
与⊙O相离.… … … … …( )
6 、若C为⊙O内与O点不重合的一点,
则直线CO与⊙O相交.( )
×√若C为⊙O内的一点,A为任意一点,
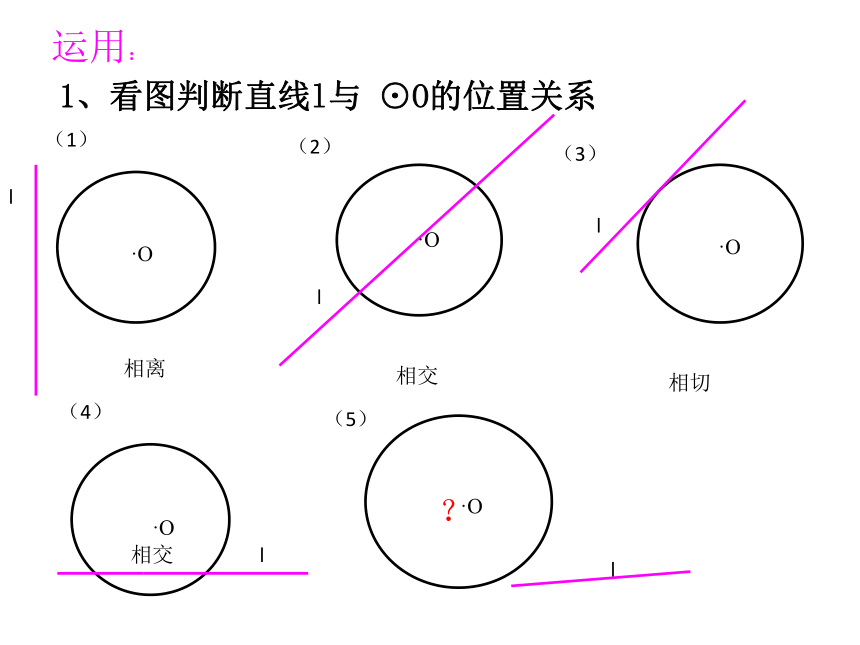
则直线AC与⊙O一定相交.是否正确?想一想?.C运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?lllll·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?·
A·
B<
<
<
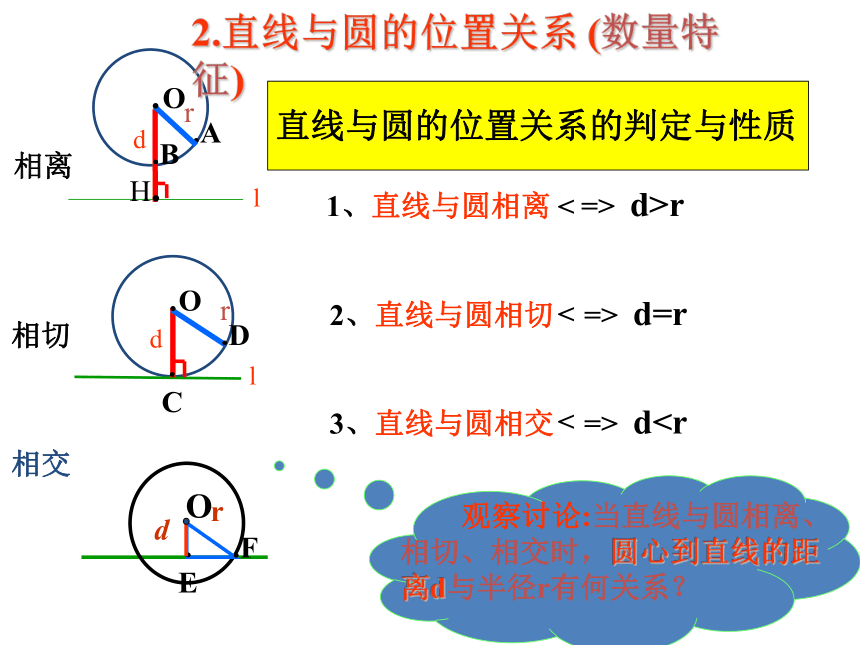
dr相离.Adr相切llH.1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => dC.O.B直线与圆的位置关系的判定与性质.
E.FO总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据判定,由_________________ ______________的关系来判断.在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r解决问题1: 设⊙O的半径为r,直线a上一点到圆心的距离为d,若d=r,则直线a与⊙O的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)相切或相交D?
解决问题2:已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .解决问题3:直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .d>5r>8思考:求圆心A到X轴、
Y轴的距离各是多少?A.(-3,-4)O解决问题4: 已知⊙A的直径为6,点A的坐标为
(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。BC43相离相切例题在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。解后思在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当 r 满足____________时,⊙C与直线AB相离。2、当 r 满足___________ 时,⊙C与直线AB相切。3、当 r 满足_________ 时,
⊙C与直线AB相交。BCAD45d=2.4cm3 4、当 r 满足 ________ 时,
⊙C与线段AB只有一个公共点.讨论在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆.1、当r满足________________时,
⊙C与直线AB相离.2、当r满足____________ 时,
⊙C与直线AB相切.3、当r满足____________时,
⊙C与直线AB相交.BCAD45d=2.4cm30cmAC=3cm,BC=4cm,
以C为圆心,r为半径作圆.想一想? 当r满足___________
_____________时,⊙C与线
段AB只有一个公共点. r=2.4cm或 3cm∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.课堂练习.OABM课堂练习 2.如图,已知∠AOB=β(β为锐角) ,M为OB上一点,且OM=5cm,以M为圆心、以2.5为半径作圆
(1)⊙M与直线OA的位置关系由 大小决定.
(2)若⊙M与直线OA相切,则β=
(3)若⊙M与直线OA相交,则β的取值范围是β30°0°≤β≤30°β0°<β<30°三、过已知圆上一点画圆的切线.O.A1、连接OAl┐2、过点A作直线l与OA垂直∴直线l就是所作的切线作法:小结:0d>r1d=r切点切线2d1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离填空题:(1)如果⊙O的半径为r,圆心O到直线L的距离为d,若L与⊙O相离,则d r;若d = r,则L与⊙O ;若直线L与⊙O相交,则 。(2)已知⊙O的半径为5㎝,O到直线L的距离为d,当d = 4㎝时,直线L与⊙O ,当d = 时,直线L与⊙O 相切,当d = 6㎝时,直线L与⊙O 。(4)在△ABC中,∠C = 90°,AB = 6 ㎝,BC = 4 ㎝,以A为圆心,4 ㎝为半径作圆,则直线BC与⊙A的位置关系是 。 相交5㎝相离相离、相切、相交相离相切>d若d、R是方程x2-9x+20=0的两个根,则直线
m和⊙O的位置关系为____________;若d、R
是方程X2-4x+m=0的两根,且直线m与⊙O相
切,则m的值为_______。想一想相交或相离4ABA 1、已知⊙O半径R=3,O点到L的距离为d,且d是方程X2-5X+6=0的一个根,则L与⊙O的位置关系是 。
相切或相交 2、在直角坐标系中,以A(2,-3)为圆心,2为半径画圆,⊙A与x轴的位置关系为 ,⊙A与y轴的位置关系为 。相切 相离·判断: 1.若线段和圆没有公共点,该圆圆心
到线段的距离大于半径. ( )×2.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( ) √ 3、在等腰△ABC中,AB=AC=2cm,若以
A为圆心,1cm为半径的圆与BC相切,则
∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°D课外思考题:已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单 位?此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系?若把⊙A向左平移呢? [z x x k 学科网]
(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标. [z x x k 学科网]
判断呢?回顾(令OP=d )想一想 你认为直线与圆有哪些位置关系?大家看日出时,在太阳升起过程中,太阳与地平线有什么关系?(地平线)a(地平线)图 1b.A.O图 2c.
F.E.O图 3这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。直线和圆没有公共点时,叫做直线与圆相离.直线和圆有唯一公共点时,叫做直线与圆相切.直线和圆有两个公共点时,叫做直线与圆相交. 这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。1.直线与圆的位置关系 (图形特征)练习1 1、直线与圆最多有两个公共点 。… ( ) √×3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )××.C5 、若A、B是⊙O外两点, 则直线AB
与⊙O相离.… … … … …( )
6 、若C为⊙O内与O点不重合的一点,
则直线CO与⊙O相交.( )
×√若C为⊙O内的一点,A为任意一点,
则直线AC与⊙O一定相交.是否正确?想一想?.C运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?lllll·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?·
A·
B<
<
<
dr相离.Adr相切llH.1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d
E.FO总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据判定,由_________________ ______________的关系来判断.在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r解决问题1: 设⊙O的半径为r,直线a上一点到圆心的距离为d,若d=r,则直线a与⊙O的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)相切或相交D?
解决问题2:已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .解决问题3:直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .d>5r>8思考:求圆心A到X轴、
Y轴的距离各是多少?A.(-3,-4)O解决问题4: 已知⊙A的直径为6,点A的坐标为
(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。BC43相离相切例题在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。解后思在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当 r 满足____________时,⊙C与直线AB相离。2、当 r 满足___________ 时,⊙C与直线AB相切。3、当 r 满足_________ 时,
⊙C与直线AB相交。BCAD45d=2.4cm3 4、当 r 满足 ________ 时,
⊙C与线段AB只有一个公共点.讨论在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆.1、当r满足________________时,
⊙C与直线AB相离.2、当r满足____________ 时,
⊙C与直线AB相切.3、当r满足____________时,
⊙C与直线AB相交.BCAD45d=2.4cm30cm
以C为圆心,r为半径作圆.想一想? 当r满足___________
_____________时,⊙C与线
段AB只有一个公共点. r=2.4cm或 3cm
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.课堂练习.OABM课堂练习 2.如图,已知∠AOB=β(β为锐角) ,M为OB上一点,且OM=5cm,以M为圆心、以2.5为半径作圆
(1)⊙M与直线OA的位置关系由 大小决定.
(2)若⊙M与直线OA相切,则β=
(3)若⊙M与直线OA相交,则β的取值范围是β30°0°≤β≤30°β0°<β<30°三、过已知圆上一点画圆的切线.O.A1、连接OAl┐2、过点A作直线l与OA垂直∴直线l就是所作的切线作法:小结:0d>r1d=r切点切线2d
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离填空题:(1)如果⊙O的半径为r,圆心O到直线L的距离为d,若L与⊙O相离,则d r;若d = r,则L与⊙O ;若直线L与⊙O相交,则 。(2)已知⊙O的半径为5㎝,O到直线L的距离为d,当d = 4㎝时,直线L与⊙O ,当d = 时,直线L与⊙O 相切,当d = 6㎝时,直线L与⊙O 。(4)在△ABC中,∠C = 90°,AB = 6 ㎝,BC = 4 ㎝,以A为圆心,4 ㎝为半径作圆,则直线BC与⊙A的位置关系是 。 相交5㎝相离相离、相切、相交相离相切>d
m和⊙O的位置关系为____________;若d、R
是方程X2-4x+m=0的两根,且直线m与⊙O相
切,则m的值为_______。想一想相交或相离4ABA 1、已知⊙O半径R=3,O点到L的距离为d,且d是方程X2-5X+6=0的一个根,则L与⊙O的位置关系是 。
相切或相交 2、在直角坐标系中,以A(2,-3)为圆心,2为半径画圆,⊙A与x轴的位置关系为 ,⊙A与y轴的位置关系为 。相切 相离·判断: 1.若线段和圆没有公共点,该圆圆心
到线段的距离大于半径. ( )×2.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( ) √ 3、在等腰△ABC中,AB=AC=2cm,若以
A为圆心,1cm为半径的圆与BC相切,则
∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°D课外思考题:已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单 位?此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系?若把⊙A向左平移呢? [z x x k 学科网]
(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标. [z x x k 学科网]
