冀教版九年级数学下29.3切线的性质和判定课件(共33张PPT)
文档属性
| 名称 | 冀教版九年级数学下29.3切线的性质和判定课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 21:39:03 | ||
图片预览







文档简介
课件33张PPT。29.3切线的性质和判定冀教版九年级数学下册
2019年8月4日思考:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r2.前面我们已学过的切线的性质有哪些?
答:①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。思考:
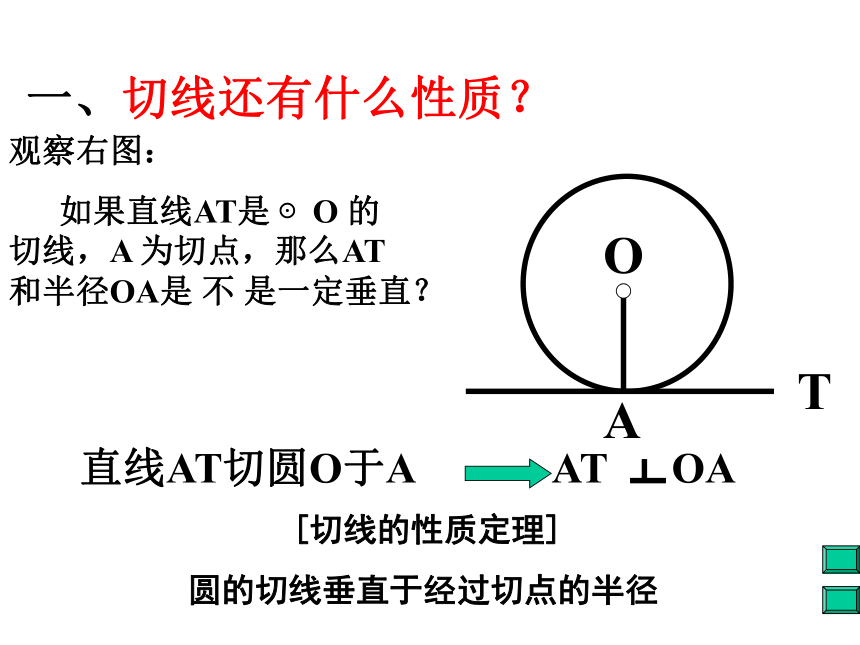
1.什么是圆的切线?判断一条直线是圆的切线的方法有那些?[切线的性质定理]
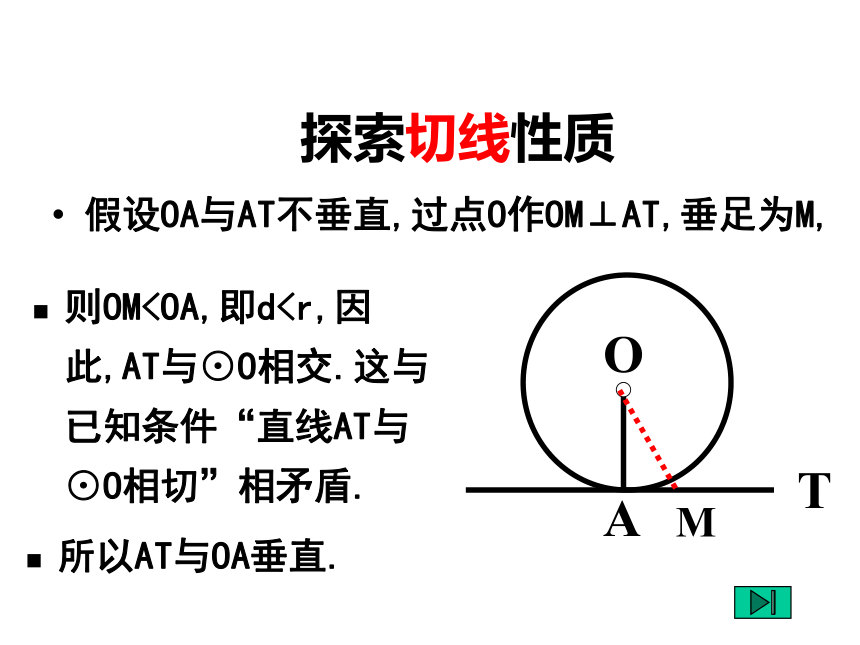
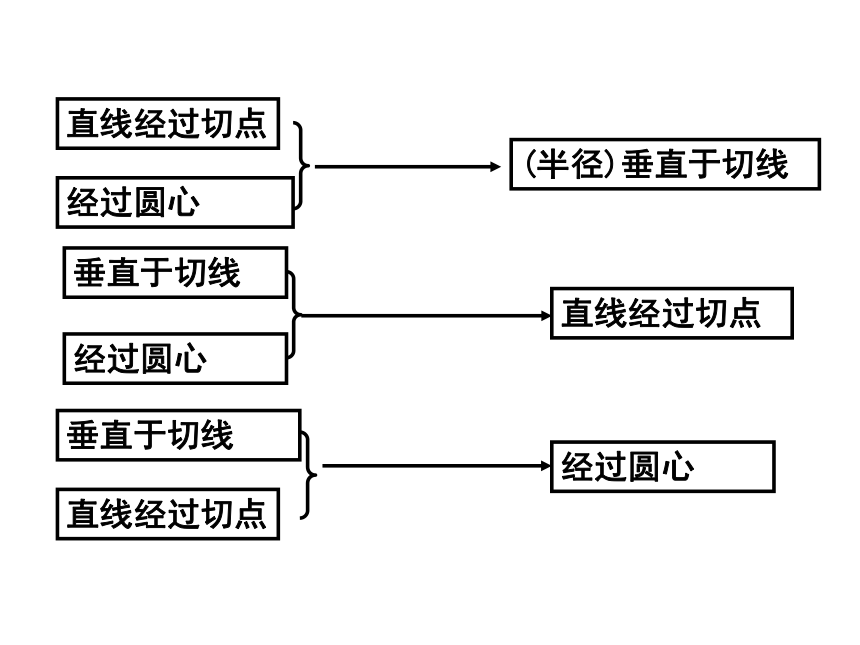
圆的切线垂直于经过切点的半径一、切线还有什么性质?观察与思考1.如图,如果一条直线经过圆心O,并且与切线AB垂直,那么这条直线经过切点T吗?为什么?1.如图,如果一条直线经过切点T,并且与切线AB垂直,那么这条直线经过圆心O吗?为什么?OBAT探索切线性质假设OA与AT不垂直,过点O作OM⊥AT,垂足为M,则OM∴沿直线AB对折图形时,AT与AD重合,因此,∠BAT=∠BAD=90°.BD作直径AB经过圆心且垂直于切线的直线必经过切点经过切点且垂直于切线的直线必经过圆心圆的切线垂直于经过切点的半径经过圆心直线经过切点垂直于切线知二推一经过圆心直线经过切点(半径)垂直于切线(3).如果AB是⊙O的切线,OA⊥AB,那么A是(2). 如果半径OA⊥AB,那么AB是按图填空:(口答)
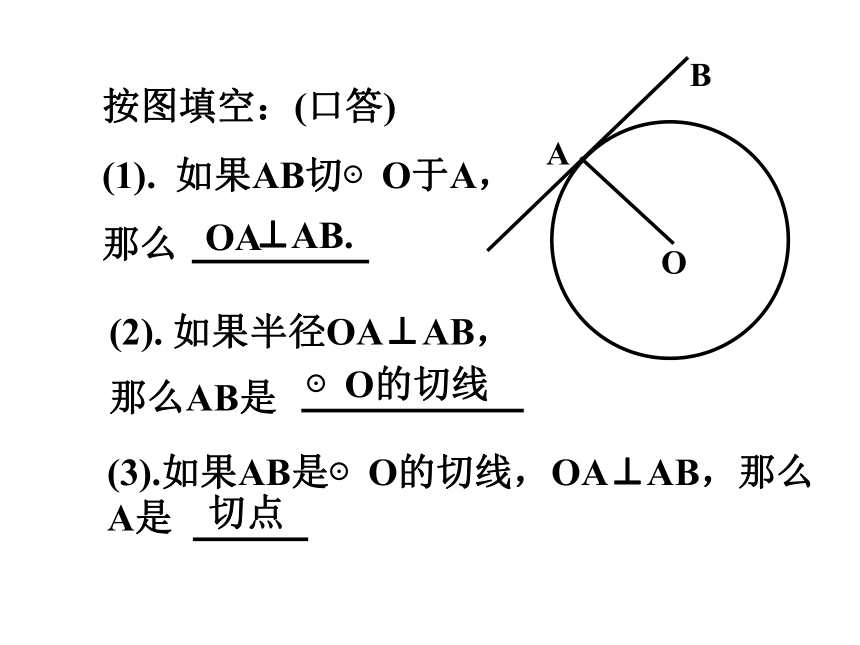
(1). 如果AB切⊙O于A,
那么AOB⊙O的切线切点练习:
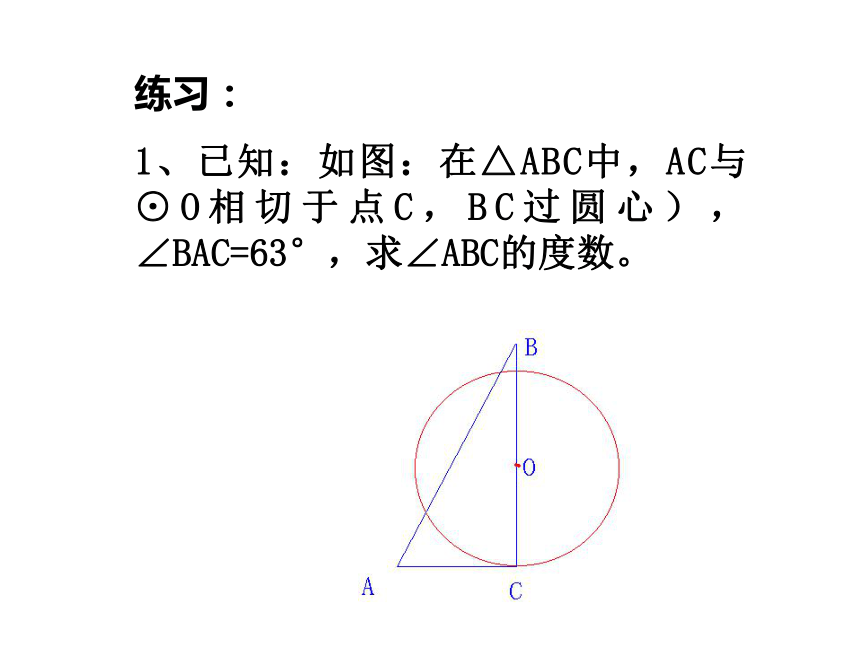
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。二、切线的判定
观察与发现
图中怎样判定直线l是⊙O的切线?答:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;思考判定一条直线是不是圆的切线除了这两种方法外,还有其它方法吗? 如图OA是⊙O的半径,过点A作直线l⊥OA,
1、用r表示半径的长,d表示圆心O到直线l的距离,那么,r和d有怎样的数量关系? 经过半径的外端并且垂直与这条半径的直线是圆的切线.切线的判断定理:2、指出直线 l和⊙O有什么位置关系?一起探究d=r 3、重新在圆上取几个点,重复上面的过程,指出过半径的外端且垂直半径的直线与⊙O的位置关系。 几何符号表达
∵ OA是半径,OA⊥l于A
∴ l是⊙O的切线。判断对错1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线 ( )××× 利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。切线的画法如图,点A是⊙O上一点,过点A作⊙O的切线l1、连结OA2、过点A画l⊥OA直线l为所画切线的画法如图,点A是⊙O外一点,过点A作⊙O的切线l1、直角三角板的一直角边经过点O2、平移三角板,使其另一直角边经过点A3、画直线l3. 如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则例:如果在地球赤道上空同样高度的位置上放置等距的三颗地球同步通信卫星,使卫星发射的信号刚好能够覆盖全部赤道,那么卫星高度应是什么?(地球半径R≈6370km) 分析:我们把赤道看成一个圆,同样高度且等距的三颗卫星的信号刚好覆盖全部赤道,等同于一个等边三角形的三边与赤道所在的圆都相切。
设三颗卫星分别位于点A,B,C处,这时,三个切点把圆三等分,每份圆弧为圆周的三分之一,
易知:∠AOD=60°。∵直线AB与圆相切于点D,
∴OD与直线AB垂直。 解:如右图:设卫星高度为h,在Rt△AOD中, cos60°= 即解这个方程,得: h=R≈6370km。 因此,当三颗卫星的高度是6370km时,信号就能够覆盖全部赤道。 一、切线的性质有哪些?
①、切线和圆有且只有一个公共点③、圆的切线垂直于经过切点的半径 ④、经过圆心且垂直于切线的直线必经过切点⑤、经过切点且垂直于切线的直线必经过圆心②、切线和圆心的距离等于半径课堂小结二、判定切线的方法有哪些?直线l 与圆有唯一公共点与圆心的距离等于圆的半径经过半径外端且垂直这条半径l是圆的切线三、 常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)l是圆的切线l是圆的切线3、三角形的内切圆与内心例1、求证:经过直径的两端点
的圆的切线互相平行。CDOAB已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD123OBACD例2、 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线4已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线。
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例1〗〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,
以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。判断一条直线是圆的切线的方法 1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。知识归纳 分析:假设符合条件的圆已经作出,那么它应当与三角形的三边都相切,这个圆的圆心到三角形的距离都等于半径,如何找到圆心?CAB 在一块三角形材料上截出一块圆形用料,怎样截才能使圆的面积最大呢? 三角形的三条角平分线交于一点,并且这个点到三条边的距离相等,因此,圆心是三角形三个内角的平分线的交点。半径的长是圆心到三角形一边的距离。内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.CABIDMNr与三角形各边都相切的圆叫做三角形的内切圆(3)以点I为圆心,ID的长为半径作⊙I ,则⊙I与△ABC的三条边都相切. ⊙I就是符合
要求的圆,
即在三角形材料上截下
的面积最大的圆。
解(1)分别作出∠B、∠C的平分线BM和CN,设他们相 交于点I(2)过点I作ID⊥BC,垂足为D如图 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长.解: 设 AF=x(cm),则AE=x,CD=CE=AC-AE=13-x,BD=BF=AB-AF=9-x,由BD+CD=BC可得(13-x)+(9-x)=14.解得 x=4cm.因此 AF=4(cm),BD=5 (cm),CE=9 (cm).证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。练 习OABCEP
2019年8月4日思考:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r2.前面我们已学过的切线的性质有哪些?
答:①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。思考:
1.什么是圆的切线?判断一条直线是圆的切线的方法有那些?[切线的性质定理]
圆的切线垂直于经过切点的半径一、切线还有什么性质?观察与思考1.如图,如果一条直线经过圆心O,并且与切线AB垂直,那么这条直线经过切点T吗?为什么?1.如图,如果一条直线经过切点T,并且与切线AB垂直,那么这条直线经过圆心O吗?为什么?OBAT探索切线性质假设OA与AT不垂直,过点O作OM⊥AT,垂足为M,则OM
(1). 如果AB切⊙O于A,
那么AOB⊙O的切线切点练习:
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。二、切线的判定
观察与发现
图中怎样判定直线l是⊙O的切线?答:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;思考判定一条直线是不是圆的切线除了这两种方法外,还有其它方法吗? 如图OA是⊙O的半径,过点A作直线l⊥OA,
1、用r表示半径的长,d表示圆心O到直线l的距离,那么,r和d有怎样的数量关系? 经过半径的外端并且垂直与这条半径的直线是圆的切线.切线的判断定理:2、指出直线 l和⊙O有什么位置关系?一起探究d=r 3、重新在圆上取几个点,重复上面的过程,指出过半径的外端且垂直半径的直线与⊙O的位置关系。 几何符号表达
∵ OA是半径,OA⊥l于A
∴ l是⊙O的切线。判断对错1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线 ( )××× 利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。切线的画法如图,点A是⊙O上一点,过点A作⊙O的切线l1、连结OA2、过点A画l⊥OA直线l为所画切线的画法如图,点A是⊙O外一点,过点A作⊙O的切线l1、直角三角板的一直角边经过点O2、平移三角板,使其另一直角边经过点A3、画直线l3. 如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则例:如果在地球赤道上空同样高度的位置上放置等距的三颗地球同步通信卫星,使卫星发射的信号刚好能够覆盖全部赤道,那么卫星高度应是什么?(地球半径R≈6370km) 分析:我们把赤道看成一个圆,同样高度且等距的三颗卫星的信号刚好覆盖全部赤道,等同于一个等边三角形的三边与赤道所在的圆都相切。
设三颗卫星分别位于点A,B,C处,这时,三个切点把圆三等分,每份圆弧为圆周的三分之一,
易知:∠AOD=60°。∵直线AB与圆相切于点D,
∴OD与直线AB垂直。 解:如右图:设卫星高度为h,在Rt△AOD中, cos60°= 即解这个方程,得: h=R≈6370km。 因此,当三颗卫星的高度是6370km时,信号就能够覆盖全部赤道。 一、切线的性质有哪些?
①、切线和圆有且只有一个公共点③、圆的切线垂直于经过切点的半径 ④、经过圆心且垂直于切线的直线必经过切点⑤、经过切点且垂直于切线的直线必经过圆心②、切线和圆心的距离等于半径课堂小结二、判定切线的方法有哪些?直线l 与圆有唯一公共点与圆心的距离等于圆的半径经过半径外端且垂直这条半径l是圆的切线三、 常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)l是圆的切线l是圆的切线3、三角形的内切圆与内心例1、求证:经过直径的两端点
的圆的切线互相平行。CDOAB已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD123OBACD例2、 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线4已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线。
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例1〗〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,
以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。判断一条直线是圆的切线的方法 1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。知识归纳 分析:假设符合条件的圆已经作出,那么它应当与三角形的三边都相切,这个圆的圆心到三角形的距离都等于半径,如何找到圆心?CAB 在一块三角形材料上截出一块圆形用料,怎样截才能使圆的面积最大呢? 三角形的三条角平分线交于一点,并且这个点到三条边的距离相等,因此,圆心是三角形三个内角的平分线的交点。半径的长是圆心到三角形一边的距离。内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.CABIDMNr与三角形各边都相切的圆叫做三角形的内切圆(3)以点I为圆心,ID的长为半径作⊙I ,则⊙I与△ABC的三条边都相切. ⊙I就是符合
要求的圆,
即在三角形材料上截下
的面积最大的圆。
解(1)分别作出∠B、∠C的平分线BM和CN,设他们相 交于点I(2)过点I作ID⊥BC,垂足为D如图 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长.解: 设 AF=x(cm),则AE=x,CD=CE=AC-AE=13-x,BD=BF=AB-AF=9-x,由BD+CD=BC可得(13-x)+(9-x)=14.解得 x=4cm.因此 AF=4(cm),BD=5 (cm),CE=9 (cm).证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。练 习OABCEP
