多边形的内角和 课件(共13张PPT)
文档属性
| 名称 | 多边形的内角和 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 21:24:30 | ||
图片预览


文档简介
课件13张PPT。《多边形的内角和》课前复习与思考:三角形的内角和是 ,
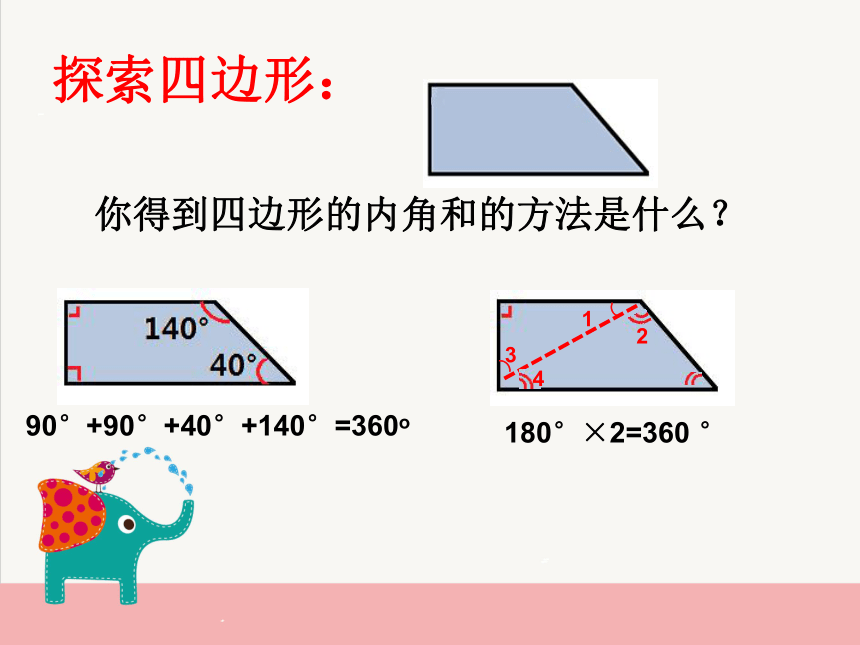
长方形和正方形的内角和是 。180°360°其他任意四边形的内角和是 ___猜一猜: 360°探索四边形:180°×2=360 °90°+90°+40°+140°=360o你得到四边形的内角和的方法是什么?探索五边形和六边形:180°×3=540°180°×4=720° 导学单1:
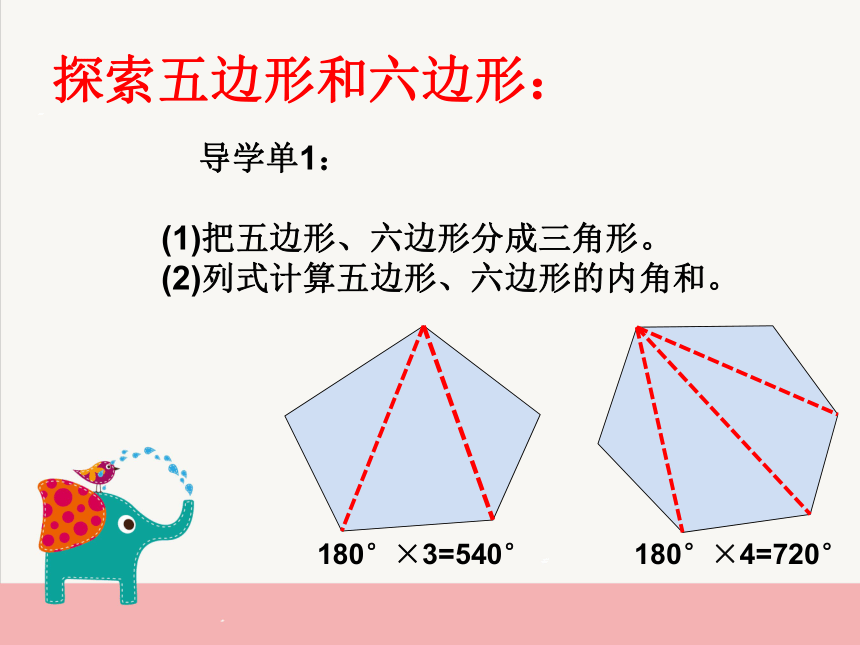
(1)把五边形、六边形分成三角形。
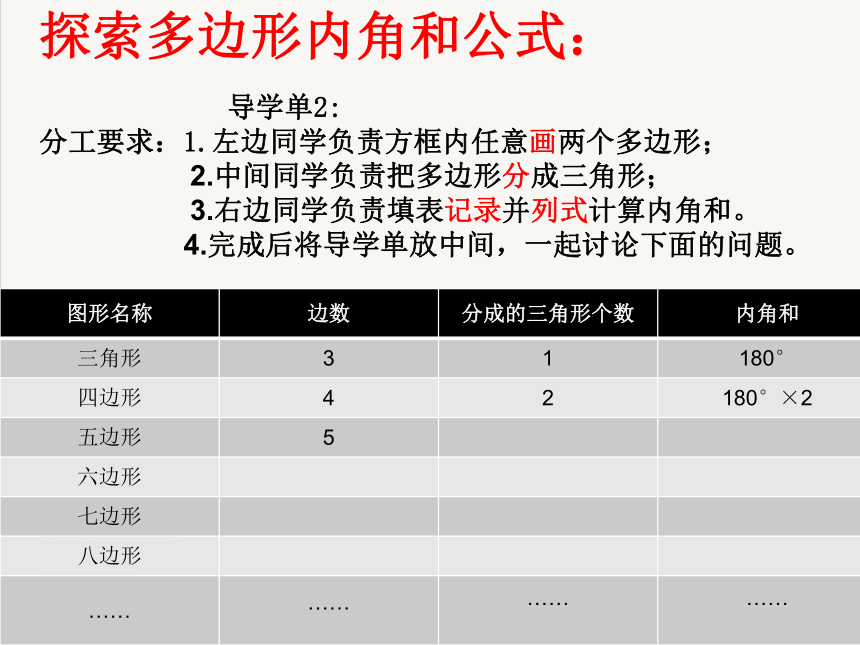
(2)列式计算五边形、六边形的内角和。探索多边形内角和公式: 导学单2:
分工要求:1.左边同学负责方框内任意画两个多边形;
2.中间同学负责把多边形分成三角形;
3.右边同学负责填表记录并列式计算内角和。
4.完成后将导学单放中间,一起讨论下面的问题。
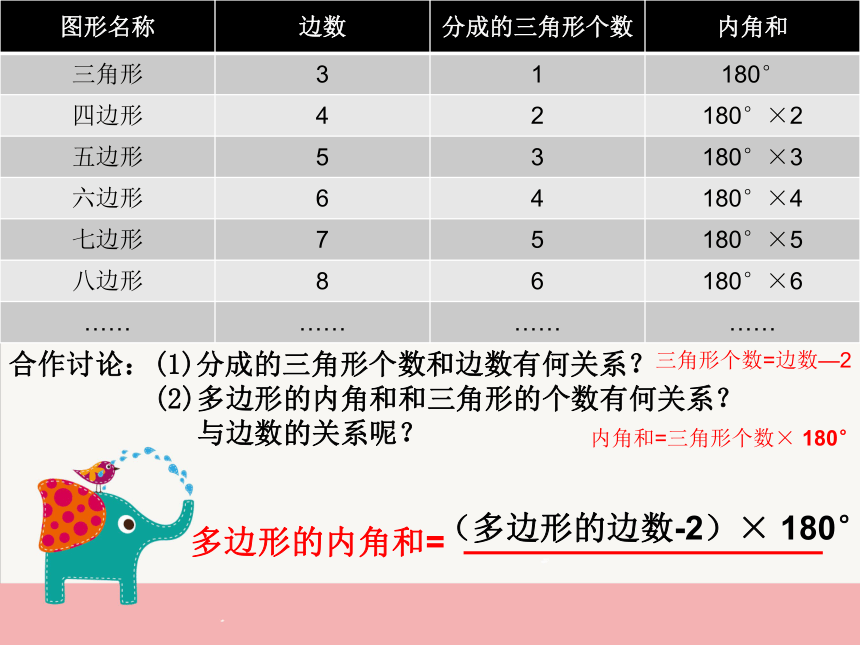
(多边形的边数-2)× 180°合作讨论:(1)分成的三角形个数和边数有何关系?
(2)多边形的内角和和三角形的个数有何关系?
与边数的关系呢?三角形个数=边数—2内角和=三角形个数× 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°在导学单3上试着分一分还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°5×180°— 360°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°5×180°— 360°4×180°— 180°=(4 -1)×180°
=(5 -2)×180°= 5×180°- 2×180°
=(5 -2)×180°=(4 -1)×180°
=(5 -2)×180°多边形的内角和=(多边形的边数-2)× 180°
(1)十二边形的内角和等于______度.
(2)一个多边形当边数增加1时,它的内角和
增加 度。
1800180检验与提升:回顾探索和发现规律的过程,
说说你的体会。总结回顾:
长方形和正方形的内角和是 。180°360°其他任意四边形的内角和是 ___猜一猜: 360°探索四边形:180°×2=360 °90°+90°+40°+140°=360o你得到四边形的内角和的方法是什么?探索五边形和六边形:180°×3=540°180°×4=720° 导学单1:
(1)把五边形、六边形分成三角形。
(2)列式计算五边形、六边形的内角和。探索多边形内角和公式: 导学单2:
分工要求:1.左边同学负责方框内任意画两个多边形;
2.中间同学负责把多边形分成三角形;
3.右边同学负责填表记录并列式计算内角和。
4.完成后将导学单放中间,一起讨论下面的问题。
(多边形的边数-2)× 180°合作讨论:(1)分成的三角形个数和边数有何关系?
(2)多边形的内角和和三角形的个数有何关系?
与边数的关系呢?三角形个数=边数—2内角和=三角形个数× 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°在导学单3上试着分一分还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°5×180°— 360°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°还有其他分割成三角形的方法吗?殊途同归:(5-2)× 180°4×180°— 180°5×180°— 360°4×180°— 180°=(4 -1)×180°
=(5 -2)×180°= 5×180°- 2×180°
=(5 -2)×180°=(4 -1)×180°
=(5 -2)×180°多边形的内角和=(多边形的边数-2)× 180°
(1)十二边形的内角和等于______度.
(2)一个多边形当边数增加1时,它的内角和
增加 度。
1800180检验与提升:回顾探索和发现规律的过程,
说说你的体会。总结回顾:
