苏科版数学七年级下册9.4乘法公式(1) 课件(30张PPT)
文档属性
| 名称 | 苏科版数学七年级下册9.4乘法公式(1) 课件(30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 279.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览











文档简介
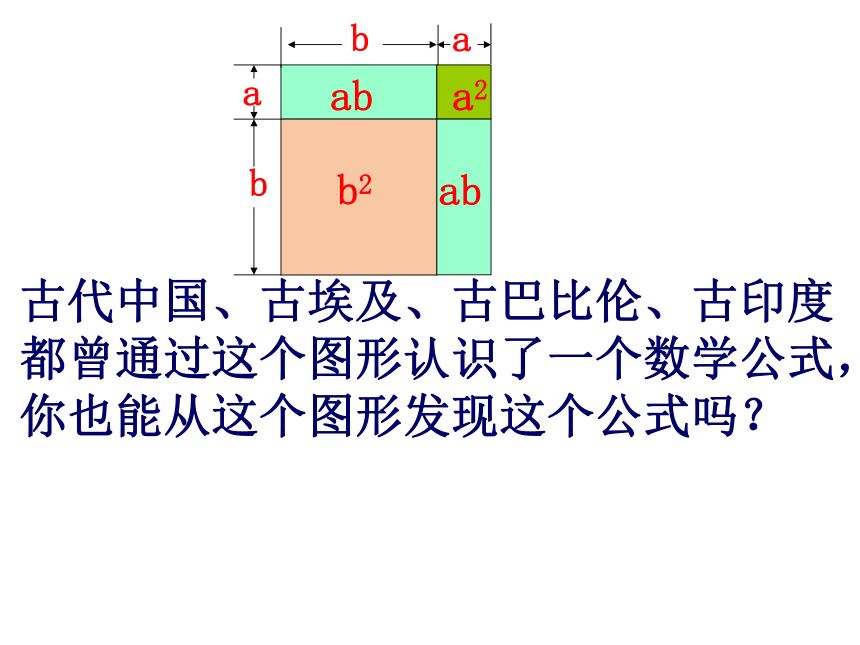
课件30张PPT。古代中国、古埃及、古巴比伦、古印度都曾通过这个图形认识了一个数学公式,你也能从这个图形发现这个公式吗?aabb9.4 乘法公式完全平方公式:
结论
(a+b)2=a2+2ab+b2情景创设:从整体看:长方形的面积为:从局部看:长方形的面积为: 你还有其他方法说明
(a+b)2=a2+2ab+b2的正确性吗?解: (a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2即 (a+b)2=a2+2ab+b2这个公式称为完全平方公式(a-b)2=a2-2ab+b2也称为完全平方公式 你怎么用所学知识计算(a-b)2?解: (a-b)2
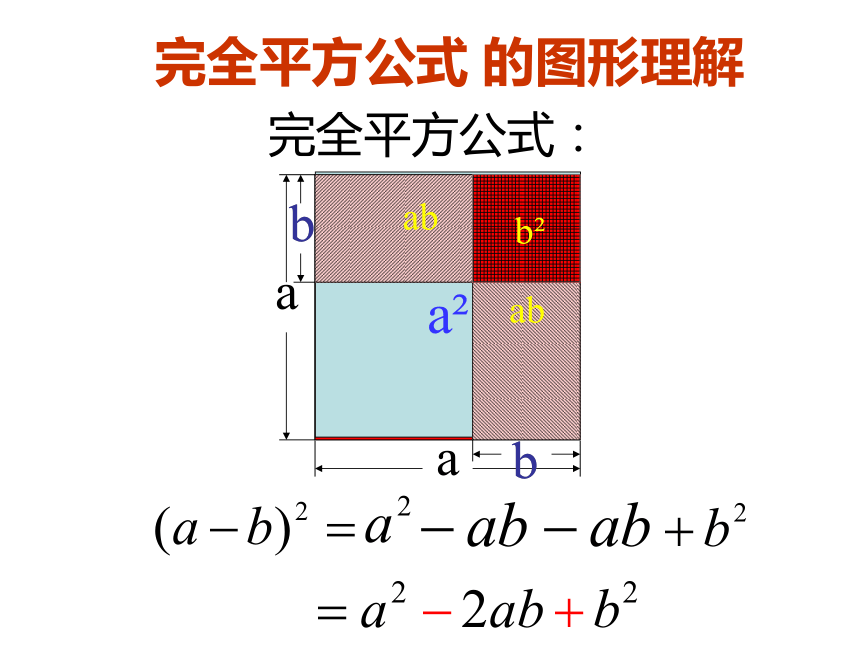
=[a+(-b)]2=a2+2·a·(-b)+(-b)2=a2-2ab+b2(a-b)2b2完全平方公式:完全平方公式 的图形理解完全平方公式:
和平方:(a+b)2=a2+2ab+b2
差平方:(a-b)2=a2-2ab+b2(1) (a+b)2=a2+2ab+b2你说说这两个公式的特点吗?(2) (a- b)2=a2 -2ab+b2“首平方、尾平方,乘积二倍放中央,符号看前方”例1:用完全平方公式计算:(1)(5+3p)2
(2)(2x-7y)2
(3)(-2a-5)2例2 运用完全平方公式进行简便计算:(1) 1042解: 1042= (100+4)2=10000+800+16=10816(2) 99.92解: 99.92= (100 –0. 1)2=10000 -20+0.01=9998.011.下面计算是否正确? (1)(x+y)2=x2+y2
(2) (-m+n)2=m2-2mn+n2
解:错误.(x+y)2=x2+2xy+y2练一练:
(3)(a+b)2=a2+ab+b2
(4) (a-1)2=a2-2a-1 解:错误.(a+b)2=a2+2ab+b2解:错误.(a-1)2=a2-2a+1练一练:2.已知a+b=2,ab=1,求a2+b2、(a-b)2的值.练一练:练一练:3.已知(a+b)2=7,
(a-b)2=4,求a2+b2,
ab的值。练一练: 边长为a的小正方形纸片放置在边长为b 的大正方形纸片上,如右图,你能用多种方法求出未被盖住的部分的面积吗? 情境创设方法(1)未被盖住的部分的面积为情境创设
方法(2):可以拼成等腰梯形,则未被盖住的部分的面积为情境创设方法(3):可以拼成长方形,则未被盖住的部分的面积为 两数和与它们的差的积等于这两个数的平方差
探索新知 你能用多项式乘法运算法则推导所得到的公式吗?一般地,对于任意的a、b,这个公式称为平方差公式平方差公式:我知道啦(a+b)(a-b)=a2-b2例1.用平方差公式计算:(1) (x+2y)(x-2y)
(2) (2x+3)(2x-3)
(3) (-5-4y)(-5+4y)一些简单变形
(1)位置变化:(a+b)(b-a)
=(b+a)(b-a)
(2)符号变化:(-3x-2y)(3x-2y)
= -(3x+2y)(3x-2y)
(3)系数变化:(3a+3b)(2a-2b)
=3(a+b)2(a-b)
=6(a+b)(a-b)(4)相同项结合,相反项结合:
(a+b-c)(a-b+c)
=[a+(b-c)][a-(b-c)]
(5)平方差公式也可逆用,有时逆用可能使计算更简便:
(2x+5)2 -(2x-5)2
=[(2x+5)+(2x-5)][(2x+5)-(2x-5)]
=4x×10
=40x1.在下列多项式乘法中,能用完全平方公式计算的请填A,能用平方差公式计算的请填B,不能用乘法公式计算的请填C.(1) (-a+2b)2 ( )
(2) (b+2a)(b-2a) ( )
(3) (1+a)(a+1) ( )
ABA练一练
(4) (-3ac+b)(3ac+b) ( )
(5) (a2-b)(a+b2) ( )
(6) ( 100-1)(100+1) ( )BCB练一练2.判断:(1)(x+3)(x-2)=x2-6 ( )(2)(x+2)(x-2)=x2-2 ( )(3)(2y+3)(-2y+3)=9-4y2 ( )(4)(3-2y)2=9-4y2 ( ) ×√××练一练3.填空:(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y23y2x4x2- 4x+3y练一练4.用完全平方公式计算(1)(2)(3)练一练完全平方公式(1) (a+b)2=a2+2ab+b2(2) (a-b)2=a2-2ab+b2平方差公式(a+b)(a+b)=a2-b2
结论
(a+b)2=a2+2ab+b2情景创设:从整体看:长方形的面积为:从局部看:长方形的面积为: 你还有其他方法说明
(a+b)2=a2+2ab+b2的正确性吗?解: (a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2即 (a+b)2=a2+2ab+b2这个公式称为完全平方公式(a-b)2=a2-2ab+b2也称为完全平方公式 你怎么用所学知识计算(a-b)2?解: (a-b)2
=[a+(-b)]2=a2+2·a·(-b)+(-b)2=a2-2ab+b2(a-b)2b2完全平方公式:完全平方公式 的图形理解完全平方公式:
和平方:(a+b)2=a2+2ab+b2
差平方:(a-b)2=a2-2ab+b2(1) (a+b)2=a2+2ab+b2你说说这两个公式的特点吗?(2) (a- b)2=a2 -2ab+b2“首平方、尾平方,乘积二倍放中央,符号看前方”例1:用完全平方公式计算:(1)(5+3p)2
(2)(2x-7y)2
(3)(-2a-5)2例2 运用完全平方公式进行简便计算:(1) 1042解: 1042= (100+4)2=10000+800+16=10816(2) 99.92解: 99.92= (100 –0. 1)2=10000 -20+0.01=9998.011.下面计算是否正确? (1)(x+y)2=x2+y2
(2) (-m+n)2=m2-2mn+n2
解:错误.(x+y)2=x2+2xy+y2练一练:
(3)(a+b)2=a2+ab+b2
(4) (a-1)2=a2-2a-1 解:错误.(a+b)2=a2+2ab+b2解:错误.(a-1)2=a2-2a+1练一练:2.已知a+b=2,ab=1,求a2+b2、(a-b)2的值.练一练:练一练:3.已知(a+b)2=7,
(a-b)2=4,求a2+b2,
ab的值。练一练: 边长为a的小正方形纸片放置在边长为b 的大正方形纸片上,如右图,你能用多种方法求出未被盖住的部分的面积吗? 情境创设方法(1)未被盖住的部分的面积为情境创设
方法(2):可以拼成等腰梯形,则未被盖住的部分的面积为情境创设方法(3):可以拼成长方形,则未被盖住的部分的面积为 两数和与它们的差的积等于这两个数的平方差
探索新知 你能用多项式乘法运算法则推导所得到的公式吗?一般地,对于任意的a、b,这个公式称为平方差公式平方差公式:我知道啦(a+b)(a-b)=a2-b2例1.用平方差公式计算:(1) (x+2y)(x-2y)
(2) (2x+3)(2x-3)
(3) (-5-4y)(-5+4y)一些简单变形
(1)位置变化:(a+b)(b-a)
=(b+a)(b-a)
(2)符号变化:(-3x-2y)(3x-2y)
= -(3x+2y)(3x-2y)
(3)系数变化:(3a+3b)(2a-2b)
=3(a+b)2(a-b)
=6(a+b)(a-b)(4)相同项结合,相反项结合:
(a+b-c)(a-b+c)
=[a+(b-c)][a-(b-c)]
(5)平方差公式也可逆用,有时逆用可能使计算更简便:
(2x+5)2 -(2x-5)2
=[(2x+5)+(2x-5)][(2x+5)-(2x-5)]
=4x×10
=40x1.在下列多项式乘法中,能用完全平方公式计算的请填A,能用平方差公式计算的请填B,不能用乘法公式计算的请填C.(1) (-a+2b)2 ( )
(2) (b+2a)(b-2a) ( )
(3) (1+a)(a+1) ( )
ABA练一练
(4) (-3ac+b)(3ac+b) ( )
(5) (a2-b)(a+b2) ( )
(6) ( 100-1)(100+1) ( )BCB练一练2.判断:(1)(x+3)(x-2)=x2-6 ( )(2)(x+2)(x-2)=x2-2 ( )(3)(2y+3)(-2y+3)=9-4y2 ( )(4)(3-2y)2=9-4y2 ( ) ×√××练一练3.填空:(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y23y2x4x2- 4x+3y练一练4.用完全平方公式计算(1)(2)(3)练一练完全平方公式(1) (a+b)2=a2+2ab+b2(2) (a-b)2=a2-2ab+b2平方差公式(a+b)(a+b)=a2-b2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
