26.3 实践与探索--二次函数中的利润问题课件
文档属性
| 名称 | 26.3 实践与探索--二次函数中的利润问题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 20:06:55 | ||
图片预览






文档简介
专题:二次函数中的利润问题
数学HS版 九年级
教学目标
1.能应用二次函数的性质解决商品销售过程中
的最大利润问题;
2.弄清商品销售问题中的数量关系及确定自变
量的取值范围。
知识回顾
1、 售价、进价、利润之间的数量关系
一罐绿豆沙售价为2.5元,进价2元,那么可以获利多少元?
如果出售100罐,又可获利多少元?
分析:
单价利润=售价-进价
总利润=(售价-进价)?销量
2、铺垫:
已知某商品的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
解:设销售单价上调了x元.
(20+x)( 300-10x) =6090
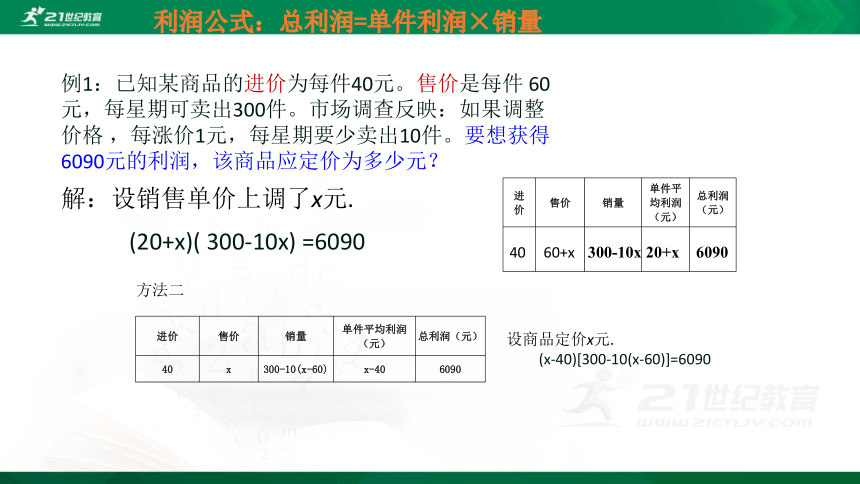
例1:已知某商品的进价为每件40元。售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
40
60+x
300-10x
20+x
6090
设商品定价x元.
(x-40)[300-10(x-60)]=6090
方法二
进价 售价 销量 单件平均利润(元) 总利润(元)
进价 售价 销量 单件平均利润(元) 总利润(元)
40 x 300-10(x-60) x-40 6090
解:设销售单价上调了x元.
利润为y元,则
y=(20+x)( 300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250
例2:已知某商品的进价为每件40元。售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得最大的利润,该商品应定价为多少元?
40
60+x
300-10x
20+x
y
∵a=-10<0
∴当x=5时y最大值=6250
此时定价为60+5=65(元)
答:要想获得最大利润,该商品应定价为65元。
若设商品定价为x元时又该如何列函数关系式?
40
x
300-10(x-60)
x-40
y
解:设销售定价为x元. 利润为y元,
则
y=(x-40)[300-10(x-60)]
=-10(x-65)2+6250
∵a=-10<0
∴当x=65时y最大值=6250
进价 售价 销量 单件平均利润(元) 总利润(元)
(1)请直接写出y与x的函数关系式;
(2)该纪念册销售单价定为多少时,文具店每周销售获得的利
润w(元)最大?最大利润是多少?
某文具店购进一批纪念册,每本的进价 为20元,售价不低于20元但不高于28元。销售过程中发现每周的销售量y(本)与每本的售价x(元)之间满足一次函数关系:当销售单价为22元时,每周的销售量为36本;当销售单价为24元时,每周的销售量为32本。
探究
解:(1)y=-2x+80(20≤x≤28)
(2)设纪念册销售单价定为x元,则
w=(x-20)y
=(x-20)(-2x+80)
=-2x2+120x-1600
=-2(x-30)2+200
∵a=-2<0,且20≤x≤28
∴当x=28时,y有最大值,此时y最大值=192
答:该纪念册销售单价定为28元时,文具店每周获得的利润最大,
最大利润为192元
方法归纳
(x-60)
(-2x+400)
拓展提升
谈谈本节课你有什么样的收获?
小结
1.设未知数,表示出销售单价、销售量、销售额、成本、总利润等量;
2.根据利润关系列出二次函数关系式,标出自变量取值范围;
3.将函数关系式化为顶点式;
4.利用二次函数最值求解,并联系实际进行检验.
1.(2018·天门)绿色生态农场生产并销售某种有机产
品,假设生产出的产品能全部售出。如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学HS版 九年级
教学目标
1.能应用二次函数的性质解决商品销售过程中
的最大利润问题;
2.弄清商品销售问题中的数量关系及确定自变
量的取值范围。
知识回顾
1、 售价、进价、利润之间的数量关系
一罐绿豆沙售价为2.5元,进价2元,那么可以获利多少元?
如果出售100罐,又可获利多少元?
分析:
单价利润=售价-进价
总利润=(售价-进价)?销量
2、铺垫:
已知某商品的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
解:设销售单价上调了x元.
(20+x)( 300-10x) =6090
例1:已知某商品的进价为每件40元。售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
40
60+x
300-10x
20+x
6090
设商品定价x元.
(x-40)[300-10(x-60)]=6090
方法二
进价 售价 销量 单件平均利润(元) 总利润(元)
进价 售价 销量 单件平均利润(元) 总利润(元)
40 x 300-10(x-60) x-40 6090
解:设销售单价上调了x元.
利润为y元,则
y=(20+x)( 300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250
例2:已知某商品的进价为每件40元。售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格?,每涨价1元,每星期要少卖出10件。要想获得最大的利润,该商品应定价为多少元?
40
60+x
300-10x
20+x
y
∵a=-10<0
∴当x=5时y最大值=6250
此时定价为60+5=65(元)
答:要想获得最大利润,该商品应定价为65元。
若设商品定价为x元时又该如何列函数关系式?
40
x
300-10(x-60)
x-40
y
解:设销售定价为x元. 利润为y元,
则
y=(x-40)[300-10(x-60)]
=-10(x-65)2+6250
∵a=-10<0
∴当x=65时y最大值=6250
进价 售价 销量 单件平均利润(元) 总利润(元)
(1)请直接写出y与x的函数关系式;
(2)该纪念册销售单价定为多少时,文具店每周销售获得的利
润w(元)最大?最大利润是多少?
某文具店购进一批纪念册,每本的进价 为20元,售价不低于20元但不高于28元。销售过程中发现每周的销售量y(本)与每本的售价x(元)之间满足一次函数关系:当销售单价为22元时,每周的销售量为36本;当销售单价为24元时,每周的销售量为32本。
探究
解:(1)y=-2x+80(20≤x≤28)
(2)设纪念册销售单价定为x元,则
w=(x-20)y
=(x-20)(-2x+80)
=-2x2+120x-1600
=-2(x-30)2+200
∵a=-2<0,且20≤x≤28
∴当x=28时,y有最大值,此时y最大值=192
答:该纪念册销售单价定为28元时,文具店每周获得的利润最大,
最大利润为192元
方法归纳
(x-60)
(-2x+400)
拓展提升
谈谈本节课你有什么样的收获?
小结
1.设未知数,表示出销售单价、销售量、销售额、成本、总利润等量;
2.根据利润关系列出二次函数关系式,标出自变量取值范围;
3.将函数关系式化为顶点式;
4.利用二次函数最值求解,并联系实际进行检验.
1.(2018·天门)绿色生态农场生产并销售某种有机产
品,假设生产出的产品能全部售出。如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
