人教版六年级数学下册第六单元《整理与复习》——练习十八(教材89---91页内容)习题课件(21张PPT)
文档属性
| 名称 | 人教版六年级数学下册第六单元《整理与复习》——练习十八(教材89---91页内容)习题课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-23 07:23:44 | ||
图片预览






文档简介
练习十八
R·六年级下册
1.判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
×
2.在括号里填上合适的计量单位。
km
m2
kg
L
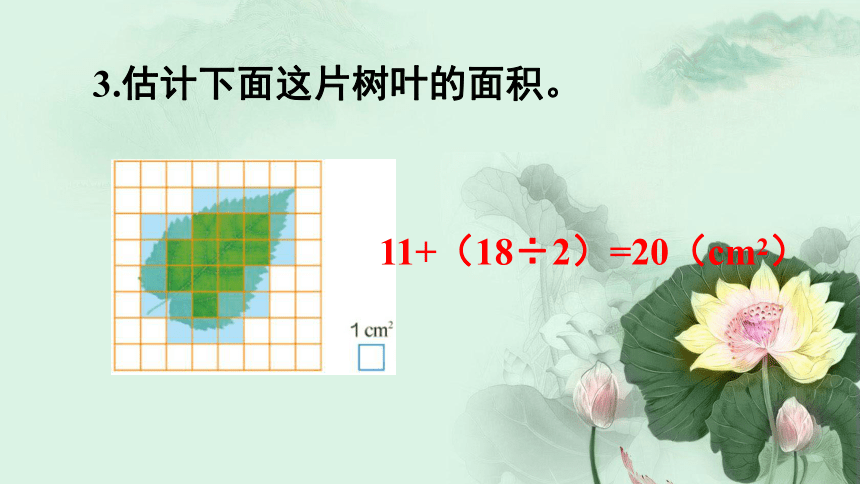
3.估计下面这片树叶的面积。
11+(18÷2)=20(cm2)
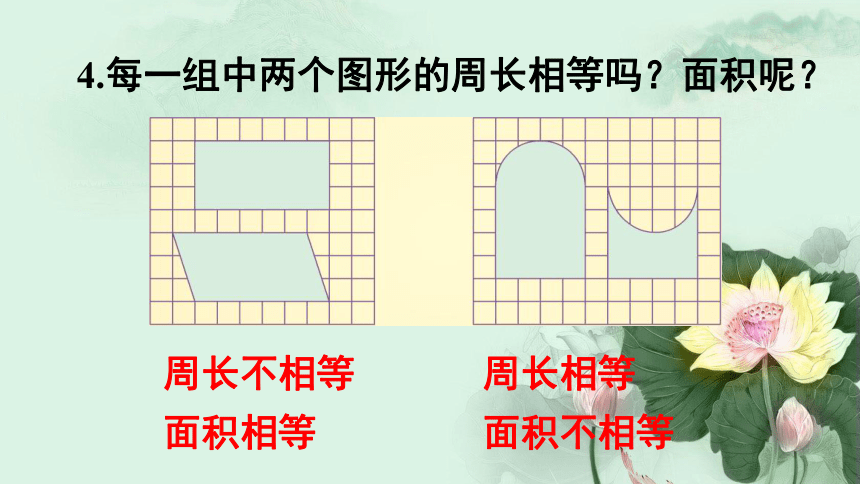
4.每一组中两个图形的周长相等吗?面积呢?
周长不相等
面积相等
周长相等
面积不相等
5.在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
略
6.一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm2,三角形的面积是多少?
30÷2=15(cm2)
答:三角形的面积是15cm2。
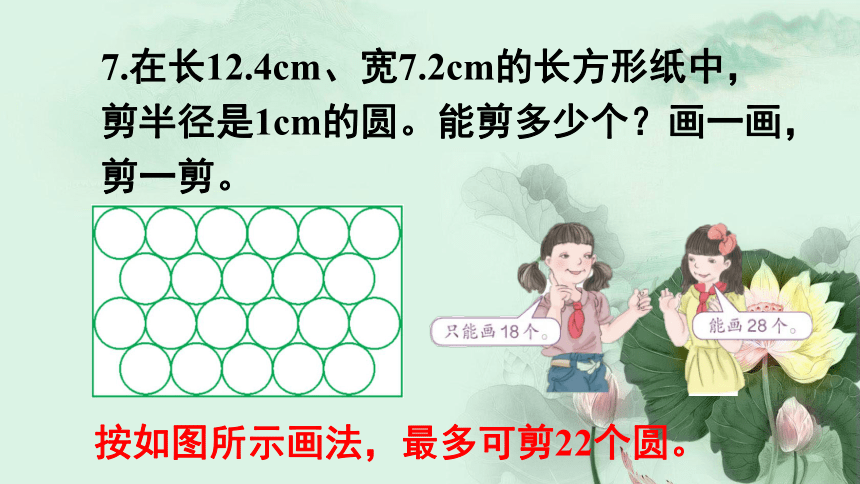
7.在长12.4cm、宽7.2cm的长方形纸中,剪半径是1cm的圆。能剪多少个?画一画,剪一剪。
按如图所示画法,最多可剪22个圆。
8.你能画一条直线把下面的每个图形分成面积相等的两部分吗?每个图形你能找出多少种画法?你能发现什么?
每个图形能画出无数个画法,发现经过图形中心点的任意一条直线都能把图形平均分成两份。
9.
下面这些图分别是从哪个方向看到的?
左面
上面
正面
10.把下面这个展开图折成一个长方体。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
F
C
10.把下面这个展开图折成一个长方体。
(3)如果要求这个长方体的表面积和体积,至少要量出哪些边的长度?
量出B面的长和宽,E面的宽。
11.把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
大正方体的体积:6×6×6=216(cm3)
小正方体的体积:2×2×2=8(cm3)
216÷8=27(个)
大正方体的表面积:6×6×6=216(cm2)
小正方体的表面积:2×2×6×27=648(cm2)
648 – 216=432(cm2)
答:可以得到27个小正方体,它们的表面积之和比原来大正方体的表面积增加了432cm2。
12.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
答:这个圆锥形铁块的高约是10cm。
13.在仓库里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如下。
这堆货物可能有多少箱?用学具摆一摆。
9箱或10箱
14.这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
表面积:20×20×5+3.14×20×20÷2+3.14×(20÷2)2=2942(cm2)
体积:20×20×20+3.14×102×20÷2=11140(cm3)
15.*右图是由棱长5cm的正方体搭成的,所有表面涂成了绿色。
(1)一共有多少个正方体?它的体积是多少?
(2)只有2个面涂色的正方体有多少个?
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个?
10个
1250cm3
2个
2个
6个
16.*一个正方体的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10÷4=7.85(cm2)
答:涂色部分的面积是7.85cm2。
17.*用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围用纸最多?
围成一个边长为2cm的正方体用的纸最多。
R·六年级下册
1.判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
×
2.在括号里填上合适的计量单位。
km
m2
kg
L
3.估计下面这片树叶的面积。
11+(18÷2)=20(cm2)
4.每一组中两个图形的周长相等吗?面积呢?
周长不相等
面积相等
周长相等
面积不相等
5.在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
略
6.一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm2,三角形的面积是多少?
30÷2=15(cm2)
答:三角形的面积是15cm2。
7.在长12.4cm、宽7.2cm的长方形纸中,剪半径是1cm的圆。能剪多少个?画一画,剪一剪。
按如图所示画法,最多可剪22个圆。
8.你能画一条直线把下面的每个图形分成面积相等的两部分吗?每个图形你能找出多少种画法?你能发现什么?
每个图形能画出无数个画法,发现经过图形中心点的任意一条直线都能把图形平均分成两份。
9.
下面这些图分别是从哪个方向看到的?
左面
上面
正面
10.把下面这个展开图折成一个长方体。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
F
C
10.把下面这个展开图折成一个长方体。
(3)如果要求这个长方体的表面积和体积,至少要量出哪些边的长度?
量出B面的长和宽,E面的宽。
11.把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
大正方体的体积:6×6×6=216(cm3)
小正方体的体积:2×2×2=8(cm3)
216÷8=27(个)
大正方体的表面积:6×6×6=216(cm2)
小正方体的表面积:2×2×6×27=648(cm2)
648 – 216=432(cm2)
答:可以得到27个小正方体,它们的表面积之和比原来大正方体的表面积增加了432cm2。
12.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
答:这个圆锥形铁块的高约是10cm。
13.在仓库里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如下。
这堆货物可能有多少箱?用学具摆一摆。
9箱或10箱
14.这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
表面积:20×20×5+3.14×20×20÷2+3.14×(20÷2)2=2942(cm2)
体积:20×20×20+3.14×102×20÷2=11140(cm3)
15.*右图是由棱长5cm的正方体搭成的,所有表面涂成了绿色。
(1)一共有多少个正方体?它的体积是多少?
(2)只有2个面涂色的正方体有多少个?
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个?
10个
1250cm3
2个
2个
6个
16.*一个正方体的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10÷4=7.85(cm2)
答:涂色部分的面积是7.85cm2。
17.*用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围用纸最多?
围成一个边长为2cm的正方体用的纸最多。
