山东省青岛市四中2018-2019年下学期九年级第一次月考数学试题(含答案)
文档属性
| 名称 | 山东省青岛市四中2018-2019年下学期九年级第一次月考数学试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 542.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览

文档简介
山东省青岛市四中2018-2019年下学期九年级数学第一次月考
数学试题
一.选择题(满分24分,每小题3分)
1.由五个相同的立方体搭成的几何体如图所示,则它的左视图是( )
A. B.
C. D.
2.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
3.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
4.反比例函数与一次函数y=2x的交点在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
5.为满足消费者需要,红星厂一月份生产手提电脑200台,计划二、三月份共生产2500台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )
A.200(1+x)2=2500
B.200(1+x)+200(1+x)2=2500
C.200(1﹣x)2=2500
D.200+200(1+x)+2000(1+x)2=250
6.在Rt△ABC中,∠C=90°,∠BAC=30°,点D是AC的中点,则tan∠DBC的值是( )
A. B. C. D.
7.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(﹣1,0),(3,0)两点,则下列说法:①abc<0;②a﹣b+c=0;③2a+b=0;④2a+c>0;⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且﹣1<x1<x2<1,x3>3,则y2<y1<y3,其中正确的结论是( )
A.①⑤ B.②④ C.②③④ D.②③⑤
8.如图,矩形ABCD,AB=8,AD=14,点M,N分别为边AD和边BC上的两点,且MN∥AB,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将△EDF沿着EF所在的直线折叠,将△CNF沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点G.以下结论中:
①EF⊥NF;②∠MNE=∠CNE;③△MNE∽△DEF;④四边形MNCD是正方形;⑤AM=5.其中正确的结论是( )
A.①② B.①④ C.①③⑤ D.①④⑤
二.填空题(共6小题,满分18分,每小题3分)
9.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.则白球有 个.
10.有一人患了流感,经过两轮传染后共有64人患了流感,那么每轮传染中平均一个人传染给 个人.
11.如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=,则CD的长为 .
12.在一场足球赛中,一球员从球门正前方10米处将球踢起射向球门,当球飞行的水平距离是6米时,球到达最高点,此时球高3米,当球飞行至球门时的高度是 米.
13.如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从点A开始出发向点C以2cm/s速度移动,点Q从B点出发向点C以1cm/s速度移动.若P,Q分别同时从A,B出发,设运动时间为t,当四边形APQB的面积是16cm2时,则t的值为 .
14.对下列现象中蕴含的数学原理阐述正确的是 (填序号)
①如图(1),剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成一个平行四边形.其依据是两组对边分别平行的四边形是平行四边形.
②如图(2),工人师傅在做矩形门窗时,不仅测量出两组对边的长度是否相等,还要测量出两条条对角线的长度相等,以确保图形是矩形.其依据是对角线相等的四边形是矩形.
③如图(3),将两张等宽的纸条放在一起,重合部分构成的四边形ABCD一定是菱形.其依据是一组邻边相等的平行四边形是菱形.
④如图(4),把一张长方形纸片按如图方式折一下,就可以裁出正方形.其依据是一组邻边相等的矩形是正方形.
三.解答题(共1小题,满分4分,每小题4分)
15.(4分)如图所示,在8×11的网格图内,建立如图平面直角坐标系,格点三角形的三个顶点为:A(﹣3,﹣1),B(1,1),C(﹣3,1).以坐标原点O为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C',(对应点在网格图内).
(1)画出△A'B'C';
(2)若△ABC的外接圆的圆心为P,⊙P以每秒1个单位的速度沿x轴正方向移动,t秒时,⊙P与A'C'第一次相切,求此时的t值.
四.解答题(共9小题,满分74分)
16.(8分)如果抛物线y=x2+2x+2k﹣4与x轴有两个不同的公共点.
(1)求k的取值范围;
(2)如果k为正整数,且该抛物线与x轴的公共点的横坐标都是整数,求k的值.
17.(6分)在△ABC中,∠C=90°.
(1)已知:c=8,∠A=60°,求∠B及a,b的值;
(2)已知:a=3,c=6,求∠A,∠B及b的值.
18.(6分)某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.某中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,求A型号电脑被选中的概率.
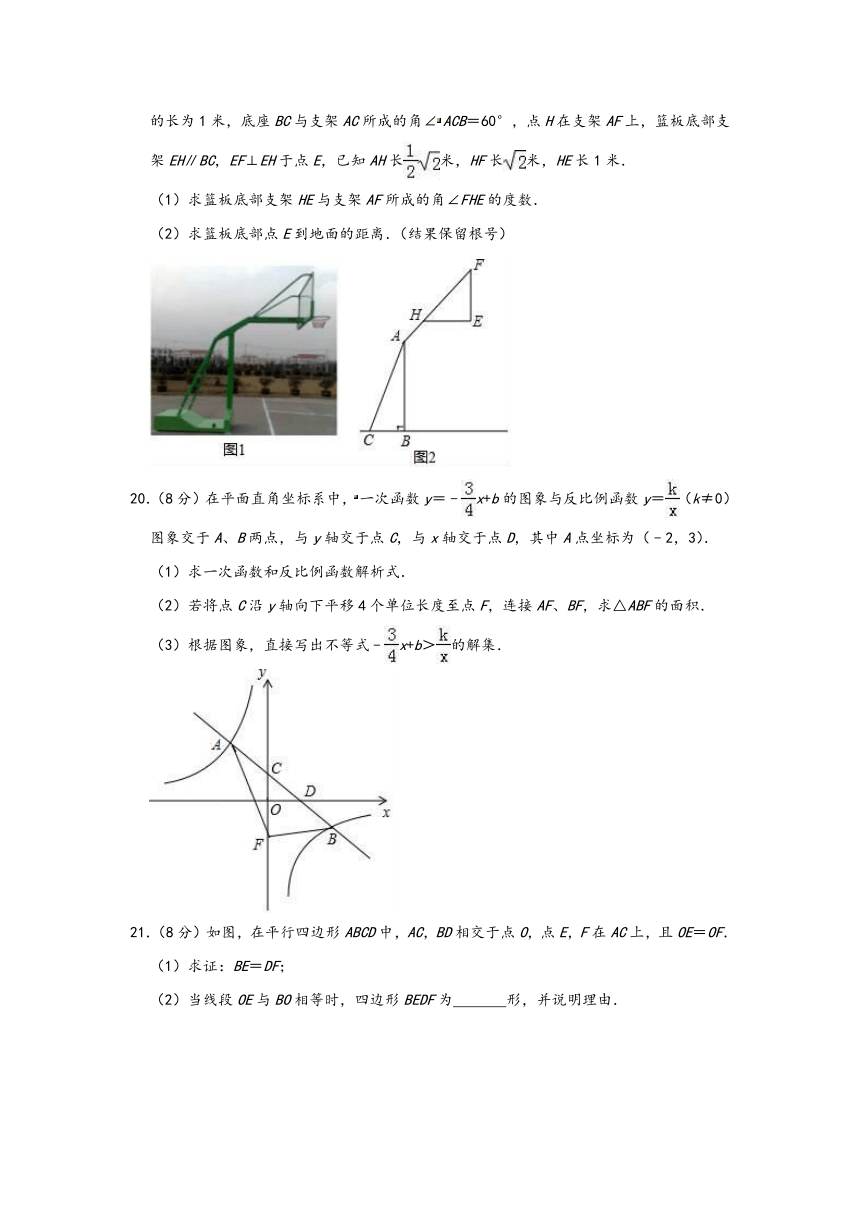
19.(6分)如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
20.(8分)在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣x+b>的解集.
21.(8分)如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
(1)求证:BE=DF;
(2)当线段OE与BO相等时,四边形BEDF为 形,并说明理由.
22.(10分)如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是 (填方案一,方案二,或方案三),则B点坐标是 ,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.
23.(10分)【几何模型】
如图(1),△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC.即: AB?r1+AC?r2=AB?h,∴r1+r2=h(定值).
【模型应用(1)】:
如图(2),在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
【模型应用(2)】:
如图(3),如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
【模型应用(3)】:
若正n边形A1、A2…An内部任意一点P到各边的距离为r1,r2,…,rn,请问是r1+r2+…+rn是否为定值?如果是,请直接写出这个定值.如果不是,请说明理由.
24.(12分)如图,在平面直角坐标系xOy中,点C(m,3)为过点A(3,0)、B(0,)的直线AB上一点,过点C的直线与x轴交于点D、与y轴交于点E,且满足∠ACE=∠COD.
(1)求点C的坐标;
(2)求直线DE的函数关系式;
(3)若直线DE上存在点M,平面内存在点N,使得A、C、M、N为顶点的四边形为菱形,请直接写出所有可能符合条件的菱形的面积.
参考答案
一.选择题
1.解:从左边看第一层是三个小正方形,第二层左边一个小正方形,
故选:D.
2.解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故选C.
3.解:∵△ABC∽△EDF,∴∠BAC=∠DEF,又∠DEF=90°+45°=135°,所以∠BAC=135°,故选D.
4.解:∵一次函数y=2x的图象经过第一、三象限,反比例函数的图象经过第一、三象限,
∴反比例函数与一次函数y=2x的交点在第一、三象限.
故选:B.
5.解:由题意可得,
200(1+x)+200(1+x)2=2500,
故选:B.
6.解:如图所示,
∵∠BAC=30°,
∴∠ABC=60°,
∴tan∠ABC==.
∵D是AC边的中点,
∴CD=AC,
∴tan∠DBC===?=.
故选:A.
7.解:①abc<0,由图象知c<0,a、b异号,所以,①错误;
②a﹣b+c=0,当x=﹣1时,y=a﹣b+c=0,正确;
③2a+b=0,函数对称轴x=﹣=1,故正确;
④2a+c>0,由②、③知:3a+c=0,而﹣a<0,∴2a+c<0,故错误;
⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且﹣1<x1<x2<1,x3>3,则y2<y1<y3,把A、B、C坐标大致在图上标出,可知正确;
故选:D.
8.解:∵由折叠的性质得,∠DFE=∠GFE,∠GFN=∠CFN,
∵∠DFE+∠GFE+∠GFN+∠CFN=180°,
∴∠GFN+∠CFN=90°,
∴∠NFE=90°,
∴EF⊥NF;故①正确;
连接AN,
∵点E是点A关于MN所在的直线的对称点,
∴∠ANM=∠ENM,
∴∠ANB=∠CNE,
而四边形ABNM不是正方形,
∴∠ANB≠∠ANM,
∴∠MNE≠∠CNE;故②错误;
∵∠NEF≠90°,∠DFE+∠DEF=90°,∠DEF+∠MEN≠90°,
∴∠DFE≠∠NEM,
∴△MNE∽△DEF错误,故③错误;
设DE=x,
∴BN=AM=,
∴CN=14﹣BN=,
∵∠EFD+∠CFN=∠EFD+∠DEF=90°,
∴∠DEF=∠CFN,
∵∠D=∠C=90°,
∴△DEF∽△CFN,
∴=,
∵F是CD的在中点,
∴CF=DF=4,
∴=,
∴x=2,x=﹣16(不合题意舍去),
∴DE=2,CN=8,
∴CD=CN,
∴四边形MNCD是正方形;故④正确;
∵CN=DM=8,
∴AM=6,故⑤错误,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
9.解:设口袋中有x个白球,
由题意,得=,
解得x=30.
把x=30代入10+x得,10+30=40≠0,故x=30是原方程的解.
答:口袋中约有30个白球.
故答案为:30.
10.解:设每轮传染中平均一个人传染给x个人,
根据题意得:1+x+x(1+x)=64,
解得:x1=7,x2=﹣9(不合题意,舍去).
答:每轮传染中平均一个人传染给7个人.
故答案为:7.
11.解:如图,过E作EM⊥AB于M,交DC于N,
∵四边形ABCD是矩形,
∴DC=AB,DC∥AB,∠ABC=90°,
∴MN=BC,EN⊥DC,
∵延AC折叠B和E重合,△AEB是等边三角形,
∴∠EAC=∠BAC=30°,
设AB=AE=BE=2a,则BC=a,即MN=a,
∵△ABE是等边三角形,EM⊥AB,
∴AM=a,由勾股定理得:EM=a,
∴△DCE的面积是×DC×EN=×2a×(a﹣a)=,
又∵S△CDE=,
∴=,
解得a=,(负值已舍去)
∴CD=2a=2,
故答案为:2.
12.解:球飞行的路线为抛物线,顶点(6,3),起点(0,0),
设抛物线的解析式为y=a(x﹣6)2+3,
∴0=a(0﹣6)2+3.
解得a=﹣.
∴抛物线的解析式为y=﹣(x﹣6)2+3,
当x=10时,y=,故球飞行至球门时的高度是: m.
故答案为:.
13.解:在△ABC中,∠C=90°,AB=10cm,AC=8cm,
∴BC==6cm.
当运动时间为t秒时,AP=2tcm,PC=(8﹣2t)cm,BQ=tcm,CQ=(6﹣t)cm,
根据题意得:×6×8﹣(8﹣2t)(6﹣t)=16,
整理得:t2﹣10t+16=0,
解得:t1=2,t2=8.
∵8﹣2t≥0,
∴t≤4,
∴t=2.
故答案为:2.
14.解:①由题意得:AB∥CD,AD∥BC,
∵两组对边分别平行,
∴四边形ABCD是平行四边形,故正确;
②∵两组对边的长度相等,
∴四边形是平行四边形,
∵对角线相等,
∴此平行四边形是矩形,故错误;
③∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为DE,DF.如图所示:
则DE=DF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD的面积=AB×DE=BC×DF,
∴AB=BC.
∴平行四边形ABCD为菱形(一组邻边相等的平行四边形是菱形),故正确;
④根据折叠原理,对折后可得:
所得的四边形有三个直角,且一组邻边相等,
所以可以裁出正方形纸片,故正确.
故答案为①③④.
三.解答题(共1小题,满分4分,每小题4分)
15.解:(1)如图,△A'B'C'为所作;
(2)如图,D点为AB的中点,⊙P与A'C'相切于E,DB=AB==,
∵△ABC为直角三角形,
∴D点为△ABC的外接圆的圆心,半径为,
∵DE=7,PE=,
∴DP=7﹣,
∴t==7﹣,
即此时t的值为7﹣.
四.解答题(共9小题,满分74分)
16.解:(1)根据题意得△=22﹣4(2k﹣4)>0,
解得k<;
(2)∵k<,
∴正整数k的值为1,2,
当k=1时,抛物线解析式为y=x2+2x﹣2,当y=0时,x2+2x﹣2=0,解得x1=﹣1+,x2=﹣1﹣,该抛物线与x轴的公共点的横坐标不是整数;
当k=2时,抛物线解析式为y=x2+2x,当y=0时,x2+2x=0,解得x1=0,x2=﹣2,该抛物线与x轴的公共点的横坐标为0和﹣2,
∴k的值为2.
17.解:(1)∵∠C=90°,
∴∠B=90°﹣∠A=90°﹣60°=30°,
∵sinA=,
∴a=csinA=8×=12,
∵tanA=,
∴b====4;
(2)在Rt△ABC中,∵sinA===,
∴∠A=45°,
∴∠B=90°﹣∠A=90°﹣45°=45°,
∴b=a=3.
18.解:(1)画树状图得:
∴有6种选择方案:AD、AE、BD、BE、CD、CE;
(2)∵(1)中各种选购方案被选中的可能性相同,且A型号电脑被选中的有2种情况,
∴A型号电脑被选中的概率==.
19.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米.
20.解:(1)∵一次函数y=﹣x+b的图象与反比例函数y=(k≠0)图象交于A(﹣3,2)、B两点,
∴3=﹣×(﹣2)+b,k=﹣2×3=﹣6
∴b=,k=﹣6
∴一次函数解析式y=﹣x+,反比例函数解析式y=
(2)根据题意得:
解得:,
∴S△ABF=×4×(4+2)=12
(3)由图象可得:x<﹣2或0<x<4
21.证明:(1)∵四边形ABCD是平行四边形,
∴OD=OB,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(SAS),
∴BE=DF.
(2)当线段OE与BO相等时,四边形BEDF为矩形,
理由:连接DE、BF.
∵OE=OF,OD=OB,
∴四边形BEDF是平行四边形,
∵OE=OB,EF=2OE,BD=2OB,
∴EF=BD,
∴四边形BEDF是矩形.
故答案为:矩.
22.解:(1)选择方案二,根据题意知点B的坐标为(10,0),
由题意知,抛物线的顶点坐标为(5,5),且经过点O(0,0),B(10,0),
设抛物线解析式为y=a(x﹣5)2+5,
把点(0,0)代入得:
0=a(0﹣5)2+5,即a=﹣,
∴抛物线解析式为y=﹣(x﹣5)2+5,
故答案为:方案二,(10,0);
(2)由题意知,当x=5﹣3=2时,﹣(x﹣5)2+5=,
所以水面上涨的高度为米.
23.模型应用(1):
解:过E点作EH⊥BC,垂足为H,连接BF,如答图(1),
∵BE=BC=3,∠EBH=45°,
∴EH=,
∵S△BFE+S△BCF=S△BEC,
∴BE×FN+BC×FM=BC×EH,
∵BE=BC,
∴FN+FM=EH=.
模型应用(2):
证明:连接PA,PB,PC,如答图(2),
∵S△PBC+S△PAC+S△PAB=S△ABC,
∴BC?r1+AC?r2+AB?r3=BC?h,
∵BC=AC=AB,
∴r1+r2+r3=h.
模型应用(3):
解:r1+r2+…+rn是定值:
r1+r2+…+rn=. …
理由参考如下(不要求学生写出):
如答图(3),
设AB为正多边形的任意一长边为a,其外接圆的半径为R,
∴a(r1+r2+…+rn)=nS△AOB,
又∵S△AOB=ah,
∴r1+r2+r3+…+rn=nh
∵Rt△BOC中,∠BOC=,
∴cos=,
∴h=Rcos=,
∴r1+r2+r3+…+rn=(定值).
24.解:(1)设直线AC解析式y=kx+b且过点A(3,0)、B(0,)
解得:k=﹣,b=
∴直线AC解析式y=﹣x+
当y=3时,3=﹣x+
∴x=﹣1
∴点C坐标(﹣1,3)
(2)
∵点A(3,0)、点C坐标(﹣1,3)
∴AC==5
∵∠ECO=∠CDO+∠COD
∴∠ECA+∠ACO=∠CDO+∠COD,且∠ACE=∠COD.
∴∠CDO=∠ACO且∠CAD=∠CAD
∴△ACO∽△ADC
∴即
∴AD=
∴DO=
∴点D(﹣,0)
设DE解析式y=mx+n过点D(﹣,0),点C坐标(﹣1,3)
∴
解得:m=,n=
∴直线DE解析式y=x+
(3)若以AC,CM为边,如图:过点D作DH⊥AC于点H,过点M作MG⊥AC于点G
∵四边形ACMN是菱形
∴AC=CM=5
∵点A(3,0),点B(0,),点C(﹣1,3),点D(﹣,0)
∴AB=,CD=
∵sin∠BAO==
∴
∴DH=5
∵DH⊥AC,MG⊥AC
∴MG∥DH
∴
∴GM==
∴菱形ACMN的面积=AC×GM=5×=
若AC为边,CM为对角线,如图:连接AN,过点C作CH⊥AD
∵四边形ACNM是菱形
∴AN⊥CM
∵S△ACD=CD×AG=AD×CH
∴×AG=
∴AG=
在Rt△ACG中,CG==
∴菱形ACNM的面积=4××CG×AG=15
若AC为对角线,如图:连接MN交AC于点G,过点A作AH⊥CD于点H
∵S△ACD=CD×AH
∴×AH=
∴AH=
∵CH=
∵四边形AMCN是菱形
∴MN⊥AC,AG=CG=
∵tan∠MCA=
∴=
∴MG=
∴菱形ACNM的面积=4××CG×MG=
数学试题
一.选择题(满分24分,每小题3分)
1.由五个相同的立方体搭成的几何体如图所示,则它的左视图是( )
A. B.
C. D.
2.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
3.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
4.反比例函数与一次函数y=2x的交点在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
5.为满足消费者需要,红星厂一月份生产手提电脑200台,计划二、三月份共生产2500台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )
A.200(1+x)2=2500
B.200(1+x)+200(1+x)2=2500
C.200(1﹣x)2=2500
D.200+200(1+x)+2000(1+x)2=250
6.在Rt△ABC中,∠C=90°,∠BAC=30°,点D是AC的中点,则tan∠DBC的值是( )
A. B. C. D.
7.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(﹣1,0),(3,0)两点,则下列说法:①abc<0;②a﹣b+c=0;③2a+b=0;④2a+c>0;⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且﹣1<x1<x2<1,x3>3,则y2<y1<y3,其中正确的结论是( )
A.①⑤ B.②④ C.②③④ D.②③⑤
8.如图,矩形ABCD,AB=8,AD=14,点M,N分别为边AD和边BC上的两点,且MN∥AB,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将△EDF沿着EF所在的直线折叠,将△CNF沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点G.以下结论中:
①EF⊥NF;②∠MNE=∠CNE;③△MNE∽△DEF;④四边形MNCD是正方形;⑤AM=5.其中正确的结论是( )
A.①② B.①④ C.①③⑤ D.①④⑤
二.填空题(共6小题,满分18分,每小题3分)
9.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.则白球有 个.
10.有一人患了流感,经过两轮传染后共有64人患了流感,那么每轮传染中平均一个人传染给 个人.
11.如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=,则CD的长为 .
12.在一场足球赛中,一球员从球门正前方10米处将球踢起射向球门,当球飞行的水平距离是6米时,球到达最高点,此时球高3米,当球飞行至球门时的高度是 米.
13.如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从点A开始出发向点C以2cm/s速度移动,点Q从B点出发向点C以1cm/s速度移动.若P,Q分别同时从A,B出发,设运动时间为t,当四边形APQB的面积是16cm2时,则t的值为 .
14.对下列现象中蕴含的数学原理阐述正确的是 (填序号)
①如图(1),剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成一个平行四边形.其依据是两组对边分别平行的四边形是平行四边形.
②如图(2),工人师傅在做矩形门窗时,不仅测量出两组对边的长度是否相等,还要测量出两条条对角线的长度相等,以确保图形是矩形.其依据是对角线相等的四边形是矩形.
③如图(3),将两张等宽的纸条放在一起,重合部分构成的四边形ABCD一定是菱形.其依据是一组邻边相等的平行四边形是菱形.
④如图(4),把一张长方形纸片按如图方式折一下,就可以裁出正方形.其依据是一组邻边相等的矩形是正方形.
三.解答题(共1小题,满分4分,每小题4分)
15.(4分)如图所示,在8×11的网格图内,建立如图平面直角坐标系,格点三角形的三个顶点为:A(﹣3,﹣1),B(1,1),C(﹣3,1).以坐标原点O为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C',(对应点在网格图内).
(1)画出△A'B'C';
(2)若△ABC的外接圆的圆心为P,⊙P以每秒1个单位的速度沿x轴正方向移动,t秒时,⊙P与A'C'第一次相切,求此时的t值.
四.解答题(共9小题,满分74分)
16.(8分)如果抛物线y=x2+2x+2k﹣4与x轴有两个不同的公共点.
(1)求k的取值范围;
(2)如果k为正整数,且该抛物线与x轴的公共点的横坐标都是整数,求k的值.
17.(6分)在△ABC中,∠C=90°.
(1)已知:c=8,∠A=60°,求∠B及a,b的值;
(2)已知:a=3,c=6,求∠A,∠B及b的值.
18.(6分)某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.某中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,求A型号电脑被选中的概率.
19.(6分)如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
20.(8分)在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣x+b>的解集.
21.(8分)如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
(1)求证:BE=DF;
(2)当线段OE与BO相等时,四边形BEDF为 形,并说明理由.
22.(10分)如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是 (填方案一,方案二,或方案三),则B点坐标是 ,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.
23.(10分)【几何模型】
如图(1),△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC.即: AB?r1+AC?r2=AB?h,∴r1+r2=h(定值).
【模型应用(1)】:
如图(2),在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
【模型应用(2)】:
如图(3),如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
【模型应用(3)】:
若正n边形A1、A2…An内部任意一点P到各边的距离为r1,r2,…,rn,请问是r1+r2+…+rn是否为定值?如果是,请直接写出这个定值.如果不是,请说明理由.
24.(12分)如图,在平面直角坐标系xOy中,点C(m,3)为过点A(3,0)、B(0,)的直线AB上一点,过点C的直线与x轴交于点D、与y轴交于点E,且满足∠ACE=∠COD.
(1)求点C的坐标;
(2)求直线DE的函数关系式;
(3)若直线DE上存在点M,平面内存在点N,使得A、C、M、N为顶点的四边形为菱形,请直接写出所有可能符合条件的菱形的面积.
参考答案
一.选择题
1.解:从左边看第一层是三个小正方形,第二层左边一个小正方形,
故选:D.
2.解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故选C.
3.解:∵△ABC∽△EDF,∴∠BAC=∠DEF,又∠DEF=90°+45°=135°,所以∠BAC=135°,故选D.
4.解:∵一次函数y=2x的图象经过第一、三象限,反比例函数的图象经过第一、三象限,
∴反比例函数与一次函数y=2x的交点在第一、三象限.
故选:B.
5.解:由题意可得,
200(1+x)+200(1+x)2=2500,
故选:B.
6.解:如图所示,
∵∠BAC=30°,
∴∠ABC=60°,
∴tan∠ABC==.
∵D是AC边的中点,
∴CD=AC,
∴tan∠DBC===?=.
故选:A.
7.解:①abc<0,由图象知c<0,a、b异号,所以,①错误;
②a﹣b+c=0,当x=﹣1时,y=a﹣b+c=0,正确;
③2a+b=0,函数对称轴x=﹣=1,故正确;
④2a+c>0,由②、③知:3a+c=0,而﹣a<0,∴2a+c<0,故错误;
⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且﹣1<x1<x2<1,x3>3,则y2<y1<y3,把A、B、C坐标大致在图上标出,可知正确;
故选:D.
8.解:∵由折叠的性质得,∠DFE=∠GFE,∠GFN=∠CFN,
∵∠DFE+∠GFE+∠GFN+∠CFN=180°,
∴∠GFN+∠CFN=90°,
∴∠NFE=90°,
∴EF⊥NF;故①正确;
连接AN,
∵点E是点A关于MN所在的直线的对称点,
∴∠ANM=∠ENM,
∴∠ANB=∠CNE,
而四边形ABNM不是正方形,
∴∠ANB≠∠ANM,
∴∠MNE≠∠CNE;故②错误;
∵∠NEF≠90°,∠DFE+∠DEF=90°,∠DEF+∠MEN≠90°,
∴∠DFE≠∠NEM,
∴△MNE∽△DEF错误,故③错误;
设DE=x,
∴BN=AM=,
∴CN=14﹣BN=,
∵∠EFD+∠CFN=∠EFD+∠DEF=90°,
∴∠DEF=∠CFN,
∵∠D=∠C=90°,
∴△DEF∽△CFN,
∴=,
∵F是CD的在中点,
∴CF=DF=4,
∴=,
∴x=2,x=﹣16(不合题意舍去),
∴DE=2,CN=8,
∴CD=CN,
∴四边形MNCD是正方形;故④正确;
∵CN=DM=8,
∴AM=6,故⑤错误,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
9.解:设口袋中有x个白球,
由题意,得=,
解得x=30.
把x=30代入10+x得,10+30=40≠0,故x=30是原方程的解.
答:口袋中约有30个白球.
故答案为:30.
10.解:设每轮传染中平均一个人传染给x个人,
根据题意得:1+x+x(1+x)=64,
解得:x1=7,x2=﹣9(不合题意,舍去).
答:每轮传染中平均一个人传染给7个人.
故答案为:7.
11.解:如图,过E作EM⊥AB于M,交DC于N,
∵四边形ABCD是矩形,
∴DC=AB,DC∥AB,∠ABC=90°,
∴MN=BC,EN⊥DC,
∵延AC折叠B和E重合,△AEB是等边三角形,
∴∠EAC=∠BAC=30°,
设AB=AE=BE=2a,则BC=a,即MN=a,
∵△ABE是等边三角形,EM⊥AB,
∴AM=a,由勾股定理得:EM=a,
∴△DCE的面积是×DC×EN=×2a×(a﹣a)=,
又∵S△CDE=,
∴=,
解得a=,(负值已舍去)
∴CD=2a=2,
故答案为:2.
12.解:球飞行的路线为抛物线,顶点(6,3),起点(0,0),
设抛物线的解析式为y=a(x﹣6)2+3,
∴0=a(0﹣6)2+3.
解得a=﹣.
∴抛物线的解析式为y=﹣(x﹣6)2+3,
当x=10时,y=,故球飞行至球门时的高度是: m.
故答案为:.
13.解:在△ABC中,∠C=90°,AB=10cm,AC=8cm,
∴BC==6cm.
当运动时间为t秒时,AP=2tcm,PC=(8﹣2t)cm,BQ=tcm,CQ=(6﹣t)cm,
根据题意得:×6×8﹣(8﹣2t)(6﹣t)=16,
整理得:t2﹣10t+16=0,
解得:t1=2,t2=8.
∵8﹣2t≥0,
∴t≤4,
∴t=2.
故答案为:2.
14.解:①由题意得:AB∥CD,AD∥BC,
∵两组对边分别平行,
∴四边形ABCD是平行四边形,故正确;
②∵两组对边的长度相等,
∴四边形是平行四边形,
∵对角线相等,
∴此平行四边形是矩形,故错误;
③∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为DE,DF.如图所示:
则DE=DF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD的面积=AB×DE=BC×DF,
∴AB=BC.
∴平行四边形ABCD为菱形(一组邻边相等的平行四边形是菱形),故正确;
④根据折叠原理,对折后可得:
所得的四边形有三个直角,且一组邻边相等,
所以可以裁出正方形纸片,故正确.
故答案为①③④.
三.解答题(共1小题,满分4分,每小题4分)
15.解:(1)如图,△A'B'C'为所作;
(2)如图,D点为AB的中点,⊙P与A'C'相切于E,DB=AB==,
∵△ABC为直角三角形,
∴D点为△ABC的外接圆的圆心,半径为,
∵DE=7,PE=,
∴DP=7﹣,
∴t==7﹣,
即此时t的值为7﹣.
四.解答题(共9小题,满分74分)
16.解:(1)根据题意得△=22﹣4(2k﹣4)>0,
解得k<;
(2)∵k<,
∴正整数k的值为1,2,
当k=1时,抛物线解析式为y=x2+2x﹣2,当y=0时,x2+2x﹣2=0,解得x1=﹣1+,x2=﹣1﹣,该抛物线与x轴的公共点的横坐标不是整数;
当k=2时,抛物线解析式为y=x2+2x,当y=0时,x2+2x=0,解得x1=0,x2=﹣2,该抛物线与x轴的公共点的横坐标为0和﹣2,
∴k的值为2.
17.解:(1)∵∠C=90°,
∴∠B=90°﹣∠A=90°﹣60°=30°,
∵sinA=,
∴a=csinA=8×=12,
∵tanA=,
∴b====4;
(2)在Rt△ABC中,∵sinA===,
∴∠A=45°,
∴∠B=90°﹣∠A=90°﹣45°=45°,
∴b=a=3.
18.解:(1)画树状图得:
∴有6种选择方案:AD、AE、BD、BE、CD、CE;
(2)∵(1)中各种选购方案被选中的可能性相同,且A型号电脑被选中的有2种情况,
∴A型号电脑被选中的概率==.
19.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米.
20.解:(1)∵一次函数y=﹣x+b的图象与反比例函数y=(k≠0)图象交于A(﹣3,2)、B两点,
∴3=﹣×(﹣2)+b,k=﹣2×3=﹣6
∴b=,k=﹣6
∴一次函数解析式y=﹣x+,反比例函数解析式y=
(2)根据题意得:
解得:,
∴S△ABF=×4×(4+2)=12
(3)由图象可得:x<﹣2或0<x<4
21.证明:(1)∵四边形ABCD是平行四边形,
∴OD=OB,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(SAS),
∴BE=DF.
(2)当线段OE与BO相等时,四边形BEDF为矩形,
理由:连接DE、BF.
∵OE=OF,OD=OB,
∴四边形BEDF是平行四边形,
∵OE=OB,EF=2OE,BD=2OB,
∴EF=BD,
∴四边形BEDF是矩形.
故答案为:矩.
22.解:(1)选择方案二,根据题意知点B的坐标为(10,0),
由题意知,抛物线的顶点坐标为(5,5),且经过点O(0,0),B(10,0),
设抛物线解析式为y=a(x﹣5)2+5,
把点(0,0)代入得:
0=a(0﹣5)2+5,即a=﹣,
∴抛物线解析式为y=﹣(x﹣5)2+5,
故答案为:方案二,(10,0);
(2)由题意知,当x=5﹣3=2时,﹣(x﹣5)2+5=,
所以水面上涨的高度为米.
23.模型应用(1):
解:过E点作EH⊥BC,垂足为H,连接BF,如答图(1),
∵BE=BC=3,∠EBH=45°,
∴EH=,
∵S△BFE+S△BCF=S△BEC,
∴BE×FN+BC×FM=BC×EH,
∵BE=BC,
∴FN+FM=EH=.
模型应用(2):
证明:连接PA,PB,PC,如答图(2),
∵S△PBC+S△PAC+S△PAB=S△ABC,
∴BC?r1+AC?r2+AB?r3=BC?h,
∵BC=AC=AB,
∴r1+r2+r3=h.
模型应用(3):
解:r1+r2+…+rn是定值:
r1+r2+…+rn=. …
理由参考如下(不要求学生写出):
如答图(3),
设AB为正多边形的任意一长边为a,其外接圆的半径为R,
∴a(r1+r2+…+rn)=nS△AOB,
又∵S△AOB=ah,
∴r1+r2+r3+…+rn=nh
∵Rt△BOC中,∠BOC=,
∴cos=,
∴h=Rcos=,
∴r1+r2+r3+…+rn=(定值).
24.解:(1)设直线AC解析式y=kx+b且过点A(3,0)、B(0,)
解得:k=﹣,b=
∴直线AC解析式y=﹣x+
当y=3时,3=﹣x+
∴x=﹣1
∴点C坐标(﹣1,3)
(2)
∵点A(3,0)、点C坐标(﹣1,3)
∴AC==5
∵∠ECO=∠CDO+∠COD
∴∠ECA+∠ACO=∠CDO+∠COD,且∠ACE=∠COD.
∴∠CDO=∠ACO且∠CAD=∠CAD
∴△ACO∽△ADC
∴即
∴AD=
∴DO=
∴点D(﹣,0)
设DE解析式y=mx+n过点D(﹣,0),点C坐标(﹣1,3)
∴
解得:m=,n=
∴直线DE解析式y=x+
(3)若以AC,CM为边,如图:过点D作DH⊥AC于点H,过点M作MG⊥AC于点G
∵四边形ACMN是菱形
∴AC=CM=5
∵点A(3,0),点B(0,),点C(﹣1,3),点D(﹣,0)
∴AB=,CD=
∵sin∠BAO==
∴
∴DH=5
∵DH⊥AC,MG⊥AC
∴MG∥DH
∴
∴GM==
∴菱形ACMN的面积=AC×GM=5×=
若AC为边,CM为对角线,如图:连接AN,过点C作CH⊥AD
∵四边形ACNM是菱形
∴AN⊥CM
∵S△ACD=CD×AG=AD×CH
∴×AG=
∴AG=
在Rt△ACG中,CG==
∴菱形ACNM的面积=4××CG×AG=15
若AC为对角线,如图:连接MN交AC于点G,过点A作AH⊥CD于点H
∵S△ACD=CD×AH
∴×AH=
∴AH=
∵CH=
∵四边形AMCN是菱形
∴MN⊥AC,AG=CG=
∵tan∠MCA=
∴=
∴MG=
∴菱形ACNM的面积=4××CG×MG=
同课章节目录
