2018-2019学年八年级下册数学19.2一次函数同步练习卷含答案
文档属性
| 名称 | 2018-2019学年八年级下册数学19.2一次函数同步练习卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-23 00:00:00 | ||
图片预览



文档简介
19.2一次函数
一、填空题
1、一次函数y= -2x+4的图象与坐标轴所围成的三角形面积是 ????????????.
2、一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是 ?? .
3、一次函数y=(m﹣1)x+m2的图象经过点(0,9),且y随x的增大而减小,则m=_____.
4、直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=_______.
5、若函数y=(a-3)x|a|-2+1是一次函数,则a=_______.
6、如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们行走3小时后,他们之间的距离为_____千米.?
二、选择题
7、若正比例函数的图象经过点(﹣1,2),则这个图象必经过点( )
A.(1,2)??? B.(﹣1,﹣2)??? C.(2,﹣1)?????? D.(1,﹣2)
8、直线y=-3x+2不经过的象限为(??? )
A.第一象限? ???? B.第二象限?? ?? C.第三象限??? ?? D.第四象限
9、在平面直角坐标系中,将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,则下列平移作法正确的是( )
A.将l1向右平移3个单位长度??? B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度??? D.将l1向上平移4个单位长度
10、已知正比例函数y=kx的图象经过第一、三象限,则一次函数y=kx﹣k的图象可能是下图中的( )
A. B.? C. D.
11、一次函数y=-x+6的图象上有两点A(-1,),B(2,),则与的大小关系是(?? )
A.=????? B. >?????? C.<?? ??? D.≥
12、对于函数y=-3x+1,下列结论正确的是( )
A.它的图象必经过点(-1,3)? ?? B.它的图象经过第一、二、三象限
C.当x>1时,y<0? ? ??? ??? D.y的值随x值的增大而增大
13、若直线y=kx+b经过第二、三、四象限,则( )
A.k>0,b>0? ?? B.k>0,b<0? ? C.k<0,b>0? ?? D.k<0,b<0
14、一次函数y=(m﹣2)x+(m﹣1)的图象如图所示,则m的取值范围是( )
A.m<2???? B.1<m<2????? C.m<1???? D.m>2
15、如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5? B.x>﹣2?? C.x>﹣3 ? D.x<﹣2
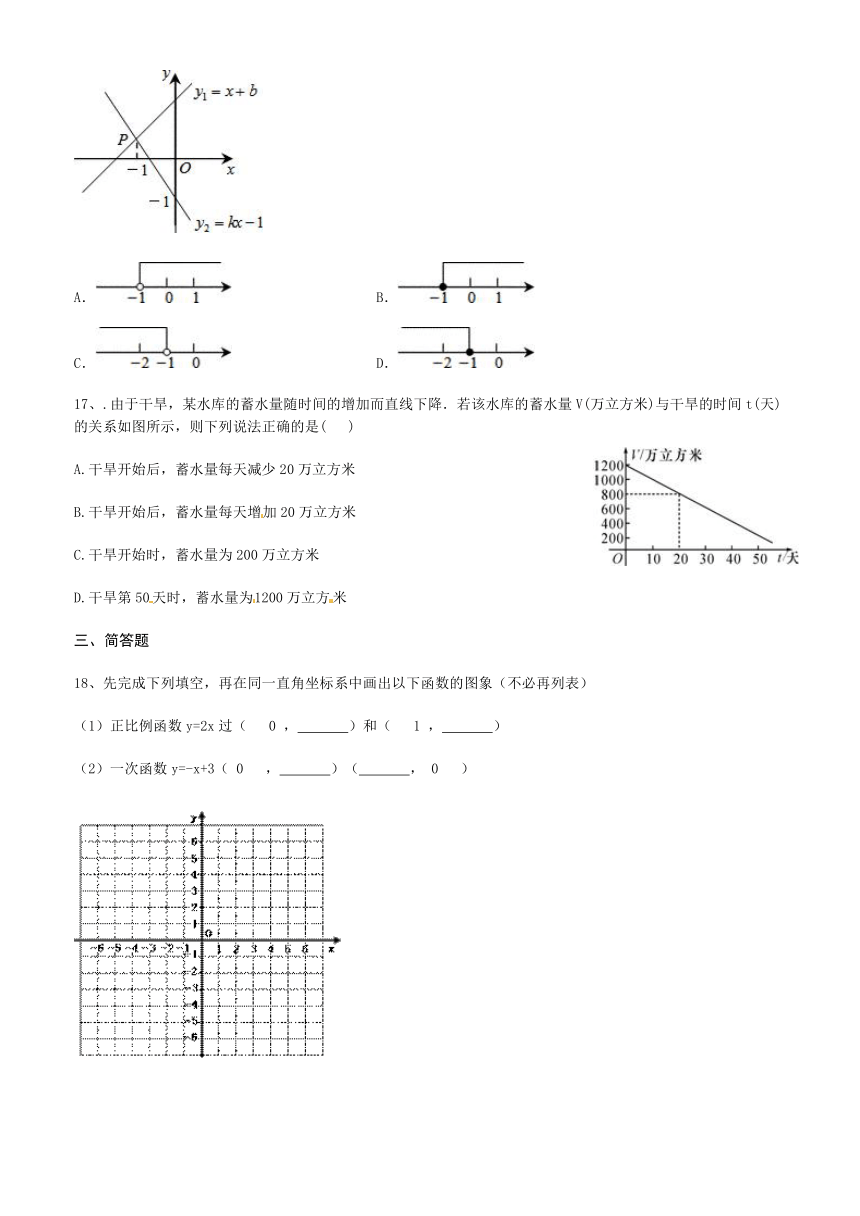
16、如图所示,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A.?? ??????? B.??
C.???????? ? D.
17、.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万立方米)与干旱的时间t(天)的关系如图所示,则下列说法正确的是(? )
A.干旱开始后,蓄水量每天减少20万立方米?
B.干旱开始后,蓄水量每天增加20万立方米
C.干旱开始时,蓄水量为200万立方米
D.干旱第50天时,蓄水量为1200万立方米
三、简答题
18、先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过(? 0 ,??? )和(? 1 ,??? )
(2)一次函数y=-x+3( 0? ,??? )(??? , 0? )?
19、已知y与x-3成正比例,当x=4时,y=3. (1)写出y与x之间的函数关系式; (2)y与x之间是什么函数关系;(3)求x=2.5时,y的值.
?
20、一次函数y=kx+4的图象过点(﹣1,7).
(1)求k的值;
(2)判断点(a,﹣3a+4)是否在该函数图象上,并说明理由.
21、小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
22、如图,直线与x轴交于点A(1,0),与 y交于点B(0,-2).
(1) 求直线AB的表达式;
(2) 点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.??????????
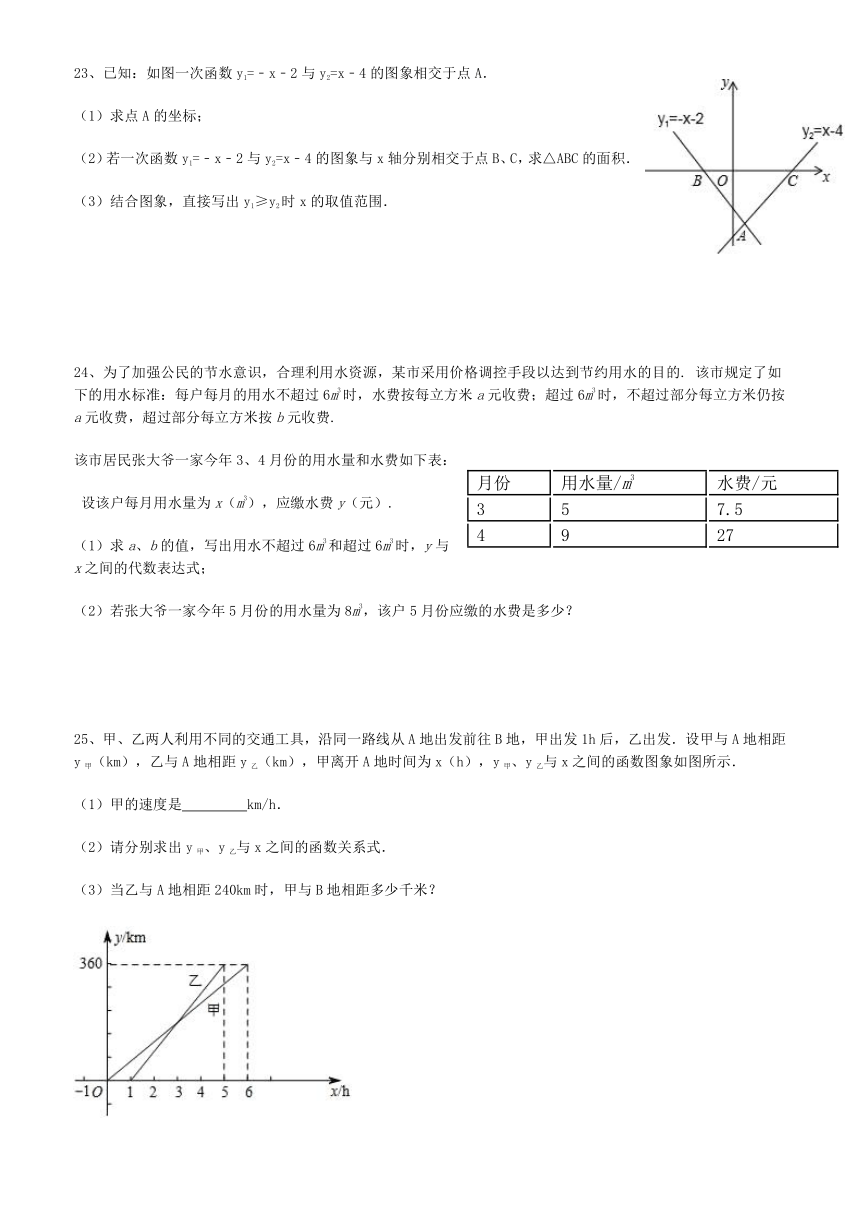
23、已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
24、为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节约用水的目的. 该市规定了如下的用水标准:每户每月的用水不超过6m3时,水费按每立方米a元收费;超过6m3时,不超过部分每立方米仍按a元收费,超过部分每立方米按b元收费.
月份 用水量/m3 水费/元
3 5 7.5
4 9 27
该市居民张大爷一家今年3、4月份的用水量和水费如下表:
设该户每月用水量为x(m3),应缴水费y(元).
(1)求a、b的值,写出用水不超过6m3和超过6m3时,y与x之间的代数表达式;
(2)若张大爷一家今年5月份的用水量为8m3,该户5月份应缴的水费是多少?
25、甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 ?? km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
参考答案
一、填空题
1、.4????
2、 x>2 .
【解答】解:根据函数图象可得出y=kx+b与x轴交于点(2,0),
所以当y<0时,x的取值范围是x>2.
故答案为:x>2.
3、﹣3.
【解析】将(0,9)代入一次函数解析式,得9=m2,m=±3,又因为y随x的增大而减小,所以m-1<0,m<1,所以m=-3.
故答案为-3.
点睛:已知一次函数上一个点的坐标要求一次函数解析式中的参数,将点的坐标代入函数解析式即可.
4、2_
5、-3_
6、_1.5__
二、选择题
7、D.8、C 9、A.10、D.11、B 12、.C 13、D
14、B解:∵一次函数y=(m﹣2)x+(m﹣1)的图象在第二、三、四象限,
∴,
解得1<m<2.故选:B.
15、B解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
则根据图象可得不等式3x+b>ax﹣3的解集是x>﹣2,
16、A 17、A
三、简答题
18、(1)0;2??? (2) 3;3? 图略
19、(1)y=3x-9; (2)一次函数;(3)y=-1.5?? (每小题2分)
?
20、【解答】解:(1)把x=﹣1,y=7代入y=kx+4中,可得:7=﹣k+4,
解得:k=﹣3,
(2)把x=a代入y=﹣3x+4中,可得:y=﹣3a+4,
所以点(a,﹣3a+4)在该函数图象上.
21、【考点】一次函数的应用.
【分析】(1)首先由小明的爸爸以96m/min速度从邮局同一条道路步行回家,求得小明的爸爸用的时间,即可得点D的坐标,然后由E(0,2400),F(25,0),利用待定系数法即可求得答案;
(2)首先求得直线BC的解析式,然后求直线BC与EF的交点,即可求得答案.
【解答】解:(1)∵小明的爸爸以96m/min速度从邮局同一条道路步行回家,
∴小明的爸爸用的时间为:?=25(min),
即OF=25,
如图:设s2与t之间的函数关系式为:s2=kt+b,
∵E(0,2400),F(25,0),
∴,
解得:,
∴s2与t之间的函数关系式为:s2=﹣96t+2400;
(2)如图:小明用了10分钟到邮局,
∴D点的坐标为(22,0),
设直线BD即s1与t之间的函数关系式为:s1=at+c(12≤t≤22),
∴,
解得:,
∴s1与t之间的函数关系式为:s1=﹣240t+5280(12≤t≤22),
当s1=s2时,小明在返回途中追上爸爸,
即﹣96t+2400=﹣240t+5280,
解得:t=20,
∴s1=s2=480,
∴小明从家出发,经过20min在返回途中追上爸爸,这时他们距离家还有480m.
22、?(1)? 解:将 A(1,0),B(0,-2)代入 得,
???????
b=-2????? k=2
直线AB的表达式是y=2x-2?????? ………………………………2′
(2)? 过点C? 作CE ⊥X 轴,垂足是E
∵CA=AB
∠BOA? = ∠AEC= 90°
∠BOA = ∠CAE
∴△BOA≌△CAE
∴CE=AB=2,? AE=OA=1???????????????????????
∴C(2,2)?????? ……………………………3′
由图示知,m<0或 m﹥2???? ……………………………5′
23、【解答】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积=×6×3=9;
(3)根据图象可知,y1≥y2时x的取值范围是x≤1.
24、解:(1)3月份用水5m3不超过6m3,所以水费按每立方米a元收取,所以5a=7.5,所以a=1.5;
4月份用水9m3,所以7.5+(9-6)·b=27,解得:b=6.5.
不超过6m3时,y=1.5x;
超过6m3时,y=7.5+6.5(x-6)
(2)由(1)可得当x=8时,y=7.5+6.5(x-6)
即y=7.5+6.5×2=20.5(元)
答:略
25、【分析】(1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法即可解决问题;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
【解答】解:(1)根据图象得:360÷6=60km/h;
故答案为60.
(2)当1≤x≤5时,设y乙=kx+b,
把(1,0)与(5,360)代入得:,
解得:k=90,b=﹣90,
则y乙=90x﹣90;
当0<x≤6时,设y甲=mx,把(6,360)代入得到m=60,
∴y甲=60x.
(3)∵乙与A地相距240km,且乙的速度为360÷(5﹣1)=90km/h,
∴乙用的时间是240÷90=h,
则甲与A地相距60×(+1)=220km.
【点评】此题考查了一次函数的应用,弄清图象中的数据是解本题的关键.
PAGE
一、填空题
1、一次函数y= -2x+4的图象与坐标轴所围成的三角形面积是 ????????????.
2、一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是 ?? .
3、一次函数y=(m﹣1)x+m2的图象经过点(0,9),且y随x的增大而减小,则m=_____.
4、直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=_______.
5、若函数y=(a-3)x|a|-2+1是一次函数,则a=_______.
6、如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们行走3小时后,他们之间的距离为_____千米.?
二、选择题
7、若正比例函数的图象经过点(﹣1,2),则这个图象必经过点( )
A.(1,2)??? B.(﹣1,﹣2)??? C.(2,﹣1)?????? D.(1,﹣2)
8、直线y=-3x+2不经过的象限为(??? )
A.第一象限? ???? B.第二象限?? ?? C.第三象限??? ?? D.第四象限
9、在平面直角坐标系中,将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,则下列平移作法正确的是( )
A.将l1向右平移3个单位长度??? B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度??? D.将l1向上平移4个单位长度
10、已知正比例函数y=kx的图象经过第一、三象限,则一次函数y=kx﹣k的图象可能是下图中的( )
A. B.? C. D.
11、一次函数y=-x+6的图象上有两点A(-1,),B(2,),则与的大小关系是(?? )
A.=????? B. >?????? C.<?? ??? D.≥
12、对于函数y=-3x+1,下列结论正确的是( )
A.它的图象必经过点(-1,3)? ?? B.它的图象经过第一、二、三象限
C.当x>1时,y<0? ? ??? ??? D.y的值随x值的增大而增大
13、若直线y=kx+b经过第二、三、四象限,则( )
A.k>0,b>0? ?? B.k>0,b<0? ? C.k<0,b>0? ?? D.k<0,b<0
14、一次函数y=(m﹣2)x+(m﹣1)的图象如图所示,则m的取值范围是( )
A.m<2???? B.1<m<2????? C.m<1???? D.m>2
15、如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5? B.x>﹣2?? C.x>﹣3 ? D.x<﹣2
16、如图所示,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A.?? ??????? B.??
C.???????? ? D.
17、.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万立方米)与干旱的时间t(天)的关系如图所示,则下列说法正确的是(? )
A.干旱开始后,蓄水量每天减少20万立方米?
B.干旱开始后,蓄水量每天增加20万立方米
C.干旱开始时,蓄水量为200万立方米
D.干旱第50天时,蓄水量为1200万立方米
三、简答题
18、先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过(? 0 ,??? )和(? 1 ,??? )
(2)一次函数y=-x+3( 0? ,??? )(??? , 0? )?
19、已知y与x-3成正比例,当x=4时,y=3. (1)写出y与x之间的函数关系式; (2)y与x之间是什么函数关系;(3)求x=2.5时,y的值.
?
20、一次函数y=kx+4的图象过点(﹣1,7).
(1)求k的值;
(2)判断点(a,﹣3a+4)是否在该函数图象上,并说明理由.
21、小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
22、如图,直线与x轴交于点A(1,0),与 y交于点B(0,-2).
(1) 求直线AB的表达式;
(2) 点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.??????????
23、已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
24、为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节约用水的目的. 该市规定了如下的用水标准:每户每月的用水不超过6m3时,水费按每立方米a元收费;超过6m3时,不超过部分每立方米仍按a元收费,超过部分每立方米按b元收费.
月份 用水量/m3 水费/元
3 5 7.5
4 9 27
该市居民张大爷一家今年3、4月份的用水量和水费如下表:
设该户每月用水量为x(m3),应缴水费y(元).
(1)求a、b的值,写出用水不超过6m3和超过6m3时,y与x之间的代数表达式;
(2)若张大爷一家今年5月份的用水量为8m3,该户5月份应缴的水费是多少?
25、甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 ?? km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
参考答案
一、填空题
1、.4????
2、 x>2 .
【解答】解:根据函数图象可得出y=kx+b与x轴交于点(2,0),
所以当y<0时,x的取值范围是x>2.
故答案为:x>2.
3、﹣3.
【解析】将(0,9)代入一次函数解析式,得9=m2,m=±3,又因为y随x的增大而减小,所以m-1<0,m<1,所以m=-3.
故答案为-3.
点睛:已知一次函数上一个点的坐标要求一次函数解析式中的参数,将点的坐标代入函数解析式即可.
4、2_
5、-3_
6、_1.5__
二、选择题
7、D.8、C 9、A.10、D.11、B 12、.C 13、D
14、B解:∵一次函数y=(m﹣2)x+(m﹣1)的图象在第二、三、四象限,
∴,
解得1<m<2.故选:B.
15、B解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
则根据图象可得不等式3x+b>ax﹣3的解集是x>﹣2,
16、A 17、A
三、简答题
18、(1)0;2??? (2) 3;3? 图略
19、(1)y=3x-9; (2)一次函数;(3)y=-1.5?? (每小题2分)
?
20、【解答】解:(1)把x=﹣1,y=7代入y=kx+4中,可得:7=﹣k+4,
解得:k=﹣3,
(2)把x=a代入y=﹣3x+4中,可得:y=﹣3a+4,
所以点(a,﹣3a+4)在该函数图象上.
21、【考点】一次函数的应用.
【分析】(1)首先由小明的爸爸以96m/min速度从邮局同一条道路步行回家,求得小明的爸爸用的时间,即可得点D的坐标,然后由E(0,2400),F(25,0),利用待定系数法即可求得答案;
(2)首先求得直线BC的解析式,然后求直线BC与EF的交点,即可求得答案.
【解答】解:(1)∵小明的爸爸以96m/min速度从邮局同一条道路步行回家,
∴小明的爸爸用的时间为:?=25(min),
即OF=25,
如图:设s2与t之间的函数关系式为:s2=kt+b,
∵E(0,2400),F(25,0),
∴,
解得:,
∴s2与t之间的函数关系式为:s2=﹣96t+2400;
(2)如图:小明用了10分钟到邮局,
∴D点的坐标为(22,0),
设直线BD即s1与t之间的函数关系式为:s1=at+c(12≤t≤22),
∴,
解得:,
∴s1与t之间的函数关系式为:s1=﹣240t+5280(12≤t≤22),
当s1=s2时,小明在返回途中追上爸爸,
即﹣96t+2400=﹣240t+5280,
解得:t=20,
∴s1=s2=480,
∴小明从家出发,经过20min在返回途中追上爸爸,这时他们距离家还有480m.
22、?(1)? 解:将 A(1,0),B(0,-2)代入 得,
???????
b=-2????? k=2
直线AB的表达式是y=2x-2?????? ………………………………2′
(2)? 过点C? 作CE ⊥X 轴,垂足是E
∵CA=AB
∠BOA? = ∠AEC= 90°
∠BOA = ∠CAE
∴△BOA≌△CAE
∴CE=AB=2,? AE=OA=1???????????????????????
∴C(2,2)?????? ……………………………3′
由图示知,m<0或 m﹥2???? ……………………………5′
23、【解答】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积=×6×3=9;
(3)根据图象可知,y1≥y2时x的取值范围是x≤1.
24、解:(1)3月份用水5m3不超过6m3,所以水费按每立方米a元收取,所以5a=7.5,所以a=1.5;
4月份用水9m3,所以7.5+(9-6)·b=27,解得:b=6.5.
不超过6m3时,y=1.5x;
超过6m3时,y=7.5+6.5(x-6)
(2)由(1)可得当x=8时,y=7.5+6.5(x-6)
即y=7.5+6.5×2=20.5(元)
答:略
25、【分析】(1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法即可解决问题;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
【解答】解:(1)根据图象得:360÷6=60km/h;
故答案为60.
(2)当1≤x≤5时,设y乙=kx+b,
把(1,0)与(5,360)代入得:,
解得:k=90,b=﹣90,
则y乙=90x﹣90;
当0<x≤6时,设y甲=mx,把(6,360)代入得到m=60,
∴y甲=60x.
(3)∵乙与A地相距240km,且乙的速度为360÷(5﹣1)=90km/h,
∴乙用的时间是240÷90=h,
则甲与A地相距60×(+1)=220km.
【点评】此题考查了一次函数的应用,弄清图象中的数据是解本题的关键.
PAGE
