19.1.2 矩形的判定 试卷
图片预览


文档简介
19.1.2矩形的判定 同步练习
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.下列结论正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.对角线互相垂直且平分的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
2.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AD=BC
3.已知平行四边形ABCD,对角线交于点O,下列条件中不一定能确定为矩形的是( )
A.∠ABC=90° B.OA=OB C.AB=BC D.AC=BD
4.在四边形ABCD中,AB∥DC,AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是( )
A.∠D=90° B.OA=4 C.AD=BC D.AB=CD
5.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
A.①②③
B.②③④
C.②⑤⑥
D.④⑤⑥
6.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
二.填空题(每小题5分,共30分)
7.木工师傅做了一张桌面,要求为长方形,现量得桌面的长为60cm,宽为32cm,对角线为66cm,这个桌面___________(填“合格”或“不合格”).
8.四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是_____________.(不再添加线或字母,写出一种情况即可)
9.对于四边形ABCD,下面给出对角线的三种特征:①AC、BD互相平分;②AC⊥BD;③AC=BD.当具备上述条件中的________,就能得到“四边形ABCD是矩形”。
10.如图,四边形ABCD的对角线AC,BD交于点O,有下列条件:①AO=CO,BO=DO;②AO=BO=CO=DO.其中能判断ABCD是矩形的条件是__________(填序号).
11. 如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为__________ 度时,四边形ABFE为矩形.
12.如图,AB∥CD,PM、PN、QM、QN分别为角平分线,则四边形PMQN是________.
三、解答题(共40分)
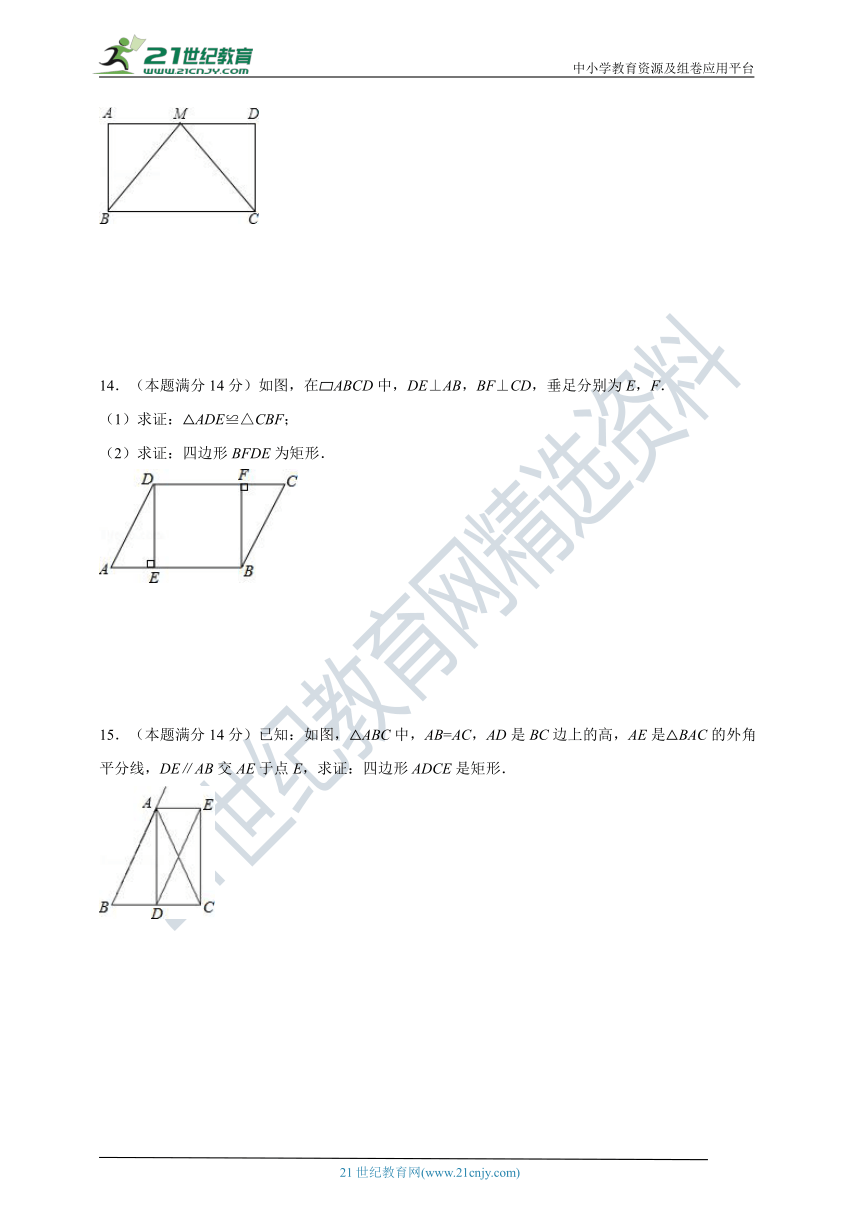
13.(本题满分12分)在?ABCD中,M为AD的中点,BM=CM,求证:四边形ABCD是矩形.
14.(本题满分14分)如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
15.(本题满分14分)已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
参考答案
一、选择题:
1.【答案】D.
【解析】A、对角线相等的四边形还可能是等腰梯形,故错误;B、对角线互相平分的四边形是平行四边形,错误;C、对角线互相垂直且平分的四边形是菱形,故错误;D、对角线互相平分且相等的四边形是矩形,故正确,故选D.
2.【答案】B.
【解析】可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,∴四边形ABCD是矩形.故选B.
3.【答案】C.
【解析】∵∠ABC=90°,∴平行四边形ABCD是矩形,故A不正确;∵OA=OB,∴AC=BD,∴平行四边形ABCD是矩形,故B,D不正确;∵AB=BC,∴平行四边形ABCD是菱形,故C正确.故选C.
4.【答案】A.
【解析】∵四边形ABCD中,AB∥DC,AD∥BC,∴四边形ABCD是平行四边形,∴当有一个角是直角时该四边形是矩形,故选A.
5.【答案】C.
【解析】A、①AB∥DC;②AB=DC可判定四边形是平行四边形,再加上③AC=BD可根据对角线相等的平行四边形是矩形进行判定,故此选项不合题意;
B、②AB=DC;③AC=BD;④∠ABC=90°,可根据题意判断出全等三角形,进而得出四边形是矩形进行判定,故此选项不合题意;
C、⑤OA=OC;⑥OB=OD可判定四边形是平行四边形,再加②AB=DC也不能判定是矩形,故此选项符合题意;
D、⑤OA=OC;⑥OB=OD可判定四边形是平行四边形,再加④∠ABC=90°可根据有一个角为直角的平行四边形是矩形进行判定,故此选项不符合题意;故选C.
6.【答案】A.
【解析】由甲同学的作业可知,CD=AB,AD=BC,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴?ABCD是矩形.所以甲的作业正确;
由乙同学的作业可知,CM=AM,MD=MB,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴?ABCD是矩形.所以乙的作业正确;故选A.
二、填空题:
7.【答案】不合格.
【解析】∵=68cm≠66cm,∴这个桌面不合格,故答案为不合格.
8.【答案】AD=BC.
【解析】添加AD=BC,∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形,∵∠D=90°,∴四边形ABCD是矩形,故答案为AD=BC.
9.【答案】①③.
【解析】当具备①③两个条件,能得到四边形ABCD是矩形.理由:∵对角线AC、BD互相平分,∴四边形ABCD为平行四边形.又∵AC=BD,∴四边形ABCD为矩形.故答案为①③.
10.【答案】②.
【解析】能判定四边形ABCD是矩形的条件为②.理由如下:AO=BO=CO=DO,∴四边形ABCD是平行四边形,∵AC=BD,∴?ABCD是矩形.故答案为②.
11.【答案】60.
【解析】如果四边形ABFE为矩形,根据矩形的性质,那么AF=BE,AC=BC,又因为AC=AB,那么三角形ABC是等边三角形,所以∠ACB=60°.故答案为60.
12.【答案】矩形.
【解析】四边形PMQN是矩形,∵PM、PN分别平分∠APQ,∠BPQ,∴∠MPQ=∠APQ,∠NPQ=∠BPQ,∵∠APQ+∠BPQ=180°,∴∠MPQ+∠NPQ=90°,∵AB∥CD,∴∠APQ=∠PQD,∵QN平分∠PQD,∴∠PQN=∠PQD,∴∠MPQ=∠NQP,∴PM∥QN,同理QM∥PN,∴四边形PMQN是平行四边形,∴四边形PMQN是矩形.故答案为矩形.
三、解答题:
13.【答案】见解析.
【解析】∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠A+∠D=180°,在△ABM和△DCM中,∵,∴△ABM≌△DCM(SSS),∴∠A=∠D=90°,即可得出平行四边形ABCD是矩形.
14.【答案】见解析
【解析】证明:(1)∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,∵四边形ABCD为平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,∵,∴△ADE≌△CBF(AAS);
(2)∵四边形ABCD为平行四边形,∴CD∥AB,∴∠CDE+∠DEB=180°,∵∠DEB=90°,∴∠CDE=90°,∴∠CDE=∠DEB=∠BFD=90°,则四边形BFDE为矩形.
15.【答案】见解析.
【解析】证明:∵AB=AC,∴∠B=∠ACB,∵AE是∠BAC的外角平分线,∴∠FAE=∠EAC,∵∠B+∠ACB=∠FAE+∠EAC,∴∠B=∠ACB=∠FAE=∠EAC,∴AE∥CD,又∵DE∥AB,∴四边形AEDB是平行四边形,∴AE平行且等于BD,又∵BD=DC,∴AE平行且等于DC,故四边形ADCE是平行四边形,又∵∠ADC=90°,∴平行四边形ADCE是矩形.即四边形ADCE是矩形.
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.下列结论正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.对角线互相垂直且平分的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
2.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AD=BC
3.已知平行四边形ABCD,对角线交于点O,下列条件中不一定能确定为矩形的是( )
A.∠ABC=90° B.OA=OB C.AB=BC D.AC=BD
4.在四边形ABCD中,AB∥DC,AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是( )
A.∠D=90° B.OA=4 C.AD=BC D.AB=CD
5.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
A.①②③
B.②③④
C.②⑤⑥
D.④⑤⑥
6.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
二.填空题(每小题5分,共30分)
7.木工师傅做了一张桌面,要求为长方形,现量得桌面的长为60cm,宽为32cm,对角线为66cm,这个桌面___________(填“合格”或“不合格”).
8.四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是_____________.(不再添加线或字母,写出一种情况即可)
9.对于四边形ABCD,下面给出对角线的三种特征:①AC、BD互相平分;②AC⊥BD;③AC=BD.当具备上述条件中的________,就能得到“四边形ABCD是矩形”。
10.如图,四边形ABCD的对角线AC,BD交于点O,有下列条件:①AO=CO,BO=DO;②AO=BO=CO=DO.其中能判断ABCD是矩形的条件是__________(填序号).
11. 如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为__________ 度时,四边形ABFE为矩形.
12.如图,AB∥CD,PM、PN、QM、QN分别为角平分线,则四边形PMQN是________.
三、解答题(共40分)
13.(本题满分12分)在?ABCD中,M为AD的中点,BM=CM,求证:四边形ABCD是矩形.
14.(本题满分14分)如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
15.(本题满分14分)已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
参考答案
一、选择题:
1.【答案】D.
【解析】A、对角线相等的四边形还可能是等腰梯形,故错误;B、对角线互相平分的四边形是平行四边形,错误;C、对角线互相垂直且平分的四边形是菱形,故错误;D、对角线互相平分且相等的四边形是矩形,故正确,故选D.
2.【答案】B.
【解析】可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,∴四边形ABCD是矩形.故选B.
3.【答案】C.
【解析】∵∠ABC=90°,∴平行四边形ABCD是矩形,故A不正确;∵OA=OB,∴AC=BD,∴平行四边形ABCD是矩形,故B,D不正确;∵AB=BC,∴平行四边形ABCD是菱形,故C正确.故选C.
4.【答案】A.
【解析】∵四边形ABCD中,AB∥DC,AD∥BC,∴四边形ABCD是平行四边形,∴当有一个角是直角时该四边形是矩形,故选A.
5.【答案】C.
【解析】A、①AB∥DC;②AB=DC可判定四边形是平行四边形,再加上③AC=BD可根据对角线相等的平行四边形是矩形进行判定,故此选项不合题意;
B、②AB=DC;③AC=BD;④∠ABC=90°,可根据题意判断出全等三角形,进而得出四边形是矩形进行判定,故此选项不合题意;
C、⑤OA=OC;⑥OB=OD可判定四边形是平行四边形,再加②AB=DC也不能判定是矩形,故此选项符合题意;
D、⑤OA=OC;⑥OB=OD可判定四边形是平行四边形,再加④∠ABC=90°可根据有一个角为直角的平行四边形是矩形进行判定,故此选项不符合题意;故选C.
6.【答案】A.
【解析】由甲同学的作业可知,CD=AB,AD=BC,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴?ABCD是矩形.所以甲的作业正确;
由乙同学的作业可知,CM=AM,MD=MB,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴?ABCD是矩形.所以乙的作业正确;故选A.
二、填空题:
7.【答案】不合格.
【解析】∵=68cm≠66cm,∴这个桌面不合格,故答案为不合格.
8.【答案】AD=BC.
【解析】添加AD=BC,∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形,∵∠D=90°,∴四边形ABCD是矩形,故答案为AD=BC.
9.【答案】①③.
【解析】当具备①③两个条件,能得到四边形ABCD是矩形.理由:∵对角线AC、BD互相平分,∴四边形ABCD为平行四边形.又∵AC=BD,∴四边形ABCD为矩形.故答案为①③.
10.【答案】②.
【解析】能判定四边形ABCD是矩形的条件为②.理由如下:AO=BO=CO=DO,∴四边形ABCD是平行四边形,∵AC=BD,∴?ABCD是矩形.故答案为②.
11.【答案】60.
【解析】如果四边形ABFE为矩形,根据矩形的性质,那么AF=BE,AC=BC,又因为AC=AB,那么三角形ABC是等边三角形,所以∠ACB=60°.故答案为60.
12.【答案】矩形.
【解析】四边形PMQN是矩形,∵PM、PN分别平分∠APQ,∠BPQ,∴∠MPQ=∠APQ,∠NPQ=∠BPQ,∵∠APQ+∠BPQ=180°,∴∠MPQ+∠NPQ=90°,∵AB∥CD,∴∠APQ=∠PQD,∵QN平分∠PQD,∴∠PQN=∠PQD,∴∠MPQ=∠NQP,∴PM∥QN,同理QM∥PN,∴四边形PMQN是平行四边形,∴四边形PMQN是矩形.故答案为矩形.
三、解答题:
13.【答案】见解析.
【解析】∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠A+∠D=180°,在△ABM和△DCM中,∵,∴△ABM≌△DCM(SSS),∴∠A=∠D=90°,即可得出平行四边形ABCD是矩形.
14.【答案】见解析
【解析】证明:(1)∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,∵四边形ABCD为平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,∵,∴△ADE≌△CBF(AAS);
(2)∵四边形ABCD为平行四边形,∴CD∥AB,∴∠CDE+∠DEB=180°,∵∠DEB=90°,∴∠CDE=90°,∴∠CDE=∠DEB=∠BFD=90°,则四边形BFDE为矩形.
15.【答案】见解析.
【解析】证明:∵AB=AC,∴∠B=∠ACB,∵AE是∠BAC的外角平分线,∴∠FAE=∠EAC,∵∠B+∠ACB=∠FAE+∠EAC,∴∠B=∠ACB=∠FAE=∠EAC,∴AE∥CD,又∵DE∥AB,∴四边形AEDB是平行四边形,∴AE平行且等于BD,又∵BD=DC,∴AE平行且等于DC,故四边形ADCE是平行四边形,又∵∠ADC=90°,∴平行四边形ADCE是矩形.即四边形ADCE是矩形.
