2019浙教版中考科学复习-物理-10、浮力计算及物体沉浮条件
文档属性
| 名称 | 2019浙教版中考科学复习-物理-10、浮力计算及物体沉浮条件 |  | |
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2019-04-23 20:18:21 | ||
图片预览



文档简介
2019浙教版中考复习物理——10、浮力计算及沉浮条件
一、 知识点
1.浮力:浸在液体(气体)中的物体,受到液体(气体)对其竖直向上的托力。
2.浮力是由于受到液体对物体向上和向下的压力之差产生的。液体的压力、压强又是由液体受到重力产生的,所以在没有重力的环境中,物体浸没在液体中不受浮力。
3.计算物体所受浮力的方法:
(1)称重测量法:F浮=G空-G液(G空是物体在空气中称重时的示数,G液是物体浸在液体中时的示数)。
(2)压力差法:F浮= F向上-F向下
(3)阿基米德原理法:F浮=G液排=ρ液gV排
(4)浮沉状态判断法:
物体悬浮:F浮=G物;ρ物=ρ液
物体漂浮:F浮=G物;ρ物<ρ液
物体下沉;F浮<G物;ρ物>ρ液
注意:(1)、 (4)本质上都属于受力分析法,利用受力分析来计算浮力是解决浮力题更加常用的方法。
二、例题精讲
【例1】★
一个盛有盐水的容器中悬浮着一个鸡蛋,容器放在斜面上,如图所示.图上画出了几个力的方向,你认为鸡蛋所受浮力的方向应是( )
A. F1 B. F2 C. F3 D. F4
【例2】★
如图所示,Q为铜制零件,其上部为边长L=0.2m的立方体,下部为边长l=0.1m的立方体.Q的下表面与容器底部粘合,且水面恰好与Q上表面相平,则零件所受的浮力为(g取10N/kg)( )
A. 0N B. 20N C. 60N D. 80N
【例3】★★
如图所示,将三个小球放入水中,A球漂浮在水面上(部分露在水面以上),B球悬浮在水中,C球沉至容器底(对容器底有压力).已知A、B两球质量相等,B、C两球体积相等.则下列说法正确的是( )
A. C球的体积大于A球的体积 B. A球所受浮力大于C球所受浮力
C. B球所受浮力大于C球所受浮力 D. 三球所受浮力相等
【例4】★★
一个木块漂浮在水面,有体积露出水面,将它放在某种液体中漂浮时,有体积露出液面,则木块的密度为________kg/m3,液体的密度为_________kg/m3.
【例5】★★
小吴同学为探究力之间的关系做了如图所示的实验.将弹簧测力计下端吊着的铝块逐渐浸入台秤上盛有水的烧杯中,直至刚没入水中(不接触容器,无水溢出).在该过程中,下列有关弹簧测力计和台秤示数的说法正确的是( )
A. 弹簧测力计的示数减小,台秤示数不变
B. 弹簧测力计的示数不变,台秤示数也不变
C. 弹簧测力计的示数减小,台秤示数增大
D. 弹簧测力计的示数不变,台秤示数增大
【例6】★★
如图所示,柱形容器的底面积为500cm2,重为5N的木块A在水中处于静止状态,此时绳子的拉力为3N,若绳子突然断了,待木块再次静止时,容器中的水面将下降( )
A. 0.6×10﹣2m B. 0.4×10﹣2m C. 1.6×10﹣2m D. 1.0×10﹣2m
【例7】★★★
质量相等的甲、乙两实心小球,密度之比ρ1:ρ2=3:2,将它们分别放入水中静止时,两球所受的浮力之比F1:F2=4:5,则乙球的密度为( )
A. ρ水 B. ρ水 C. ρ水 D. ρ水
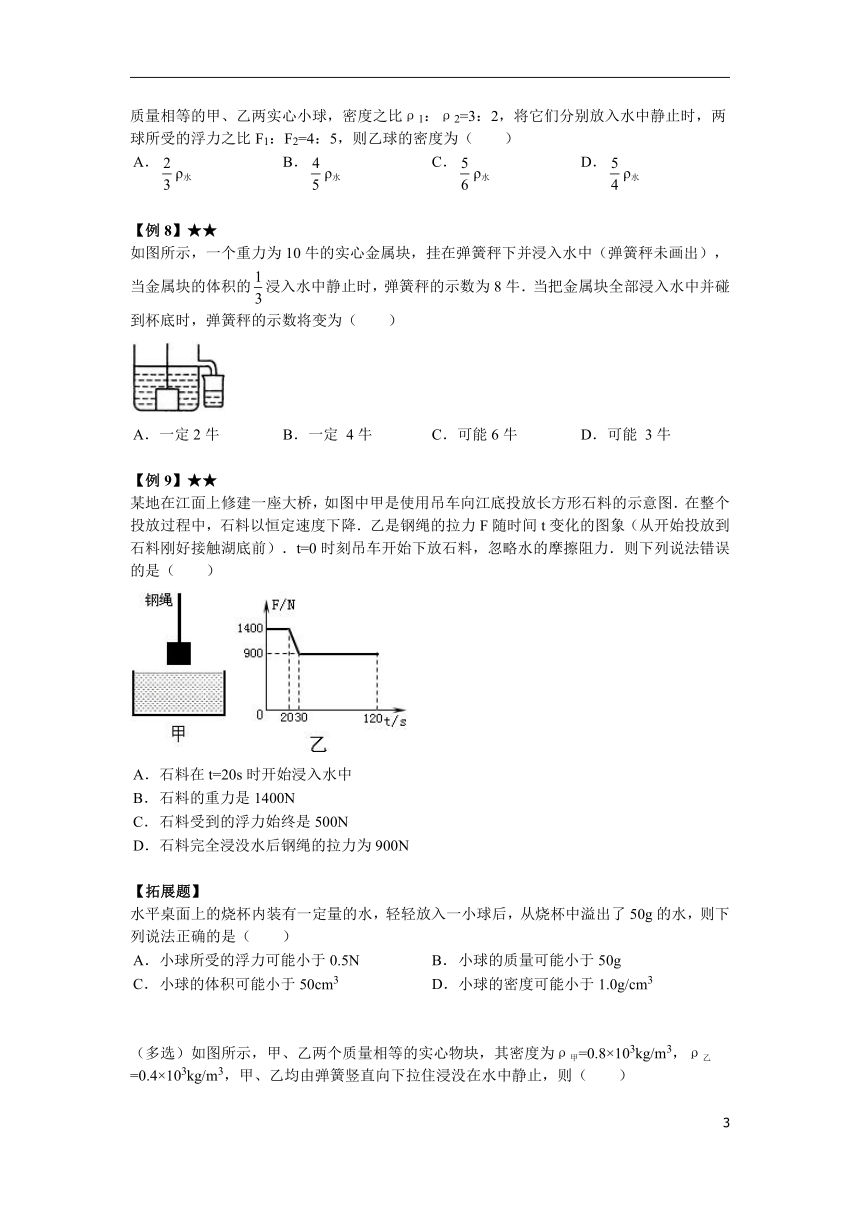
【例8】★★
如图所示,一个重力为10牛的实心金属块,挂在弹簧秤下并浸入水中(弹簧秤未画出),当金属块的体积的浸入水中静止时,弹簧秤的示数为8牛.当把金属块全部浸入水中并碰到杯底时,弹簧秤的示数将变为( )
A. 一定2牛 B. 一定 4牛 C. 可能6牛 D. 可能 3牛
【例9】★★
某地在江面上修建一座大桥,如图中甲是使用吊车向江底投放长方形石料的示意图.在整个投放过程中,石料以恒定速度下降.乙是钢绳的拉力F随时间t变化的图象(从开始投放到石料刚好接触湖底前).t=0时刻吊车开始下放石料,忽略水的摩擦阻力.则下列说法错误的是( )
A. 石料在t=20s时开始浸入水中
B. 石料的重力是1400N
C. 石料受到的浮力始终是500N
D. 石料完全浸没水后钢绳的拉力为900N
【拓展题】
水平桌面上的烧杯内装有一定量的水,轻轻放入一小球后,从烧杯中溢出了50g的水,则下列说法正确的是( )
A. 小球所受的浮力可能小于0.5N B. 小球的质量可能小于50g
C. 小球的体积可能小于50cm3 D. 小球的密度可能小于1.0g/cm3
(多选)如图所示,甲、乙两个质量相等的实心物块,其密度为ρ甲=0.8×103kg/m3,ρ乙=0.4×103kg/m3,甲、乙均由弹簧竖直向下拉住浸没在水中静止,则( )
A. 甲、乙所受浮力之比为2:1 B. 甲、乙所受浮力之比为1:2
C. 甲、乙所受弹簧拉力之比为1:6 D. 甲、乙所受弹簧拉力之比为2:3
参考答案
1、
考点: 浮力产生的原因
分析: 从浮力产生的原因和浮力的方向去解答此题.
解答: 解:鸡蛋悬浮在液体中,此时鸡蛋上、下表面受到的压力不同, 这个压力差就是鸡蛋所受浮力,因浮力的方向总是竖直向上的, 所以F3正确;故选C.
2、
考点: 浮力大小的计算.
专题: 浮力.
分析: 知道浮力的产生是上下表面的压强差,那么下部立方体由于与与容器底部粘合,水没有产生向上的压力;上部立方体的下表面积的一部分受到压力,则求出受力面积,利用p=ρgh求出下表面的压强,然后利用F=PS即可求得立方体受到水对它的浮力大小.
解答: 解:∵下部立方体由于与与容器底部粘合,∴水没有产生向上的压力; ∵上部立方体的下表面积的一部分(与水接触)受到向上的压力, ∴S=L2﹣l2=(0.2m)2﹣(0.1m)2=0.03m2, 上部立方体的下表面的压强为p=ρgh=1.0×103kg/m3×10N/kg×0.2m=2000pa, ∵浮力的产生是上下表面的压强差, ∴F浮=pS=2000Pa×0.03m2=60N. 故选C.
3、
考点: 浮力大小的计算;物体的浮沉条件及其应用.
专题: 计算题;压轴题.
分析: 知道A、B质量相等,A球漂浮、B球悬浮,利用漂浮、悬浮条件得出AB球受到的浮力关系; 知道B、C的体积相等,放入水中后,B球悬浮,C球下沉至容器底部,利用阿基米德原理比较BC两球受到的浮力关系和受到重力的关系.然后即可得出结论.
解答: 解:由图可知,A球漂浮,B球悬浮,C球下沉至容器底部, ∵A球漂浮, ∴A球受到的浮力:FA=GA=mAg, ∵B球悬浮, ∴B球受到的浮力:FB=GB=mBg, ∵mA=mB, ∴FA=FB; ∵B球悬浮,C球沉到水底,B、C的体积相等, ∴B、C球排开水的体积相同, ∵F浮=ρ水v排g, ∴B、C两球受到的浮力:FB=FC; ∴FA=FB=FC,故D正确; 故选D.
4、
考点: 物体的浮沉条件及其应用.
专题: 浮沉的应用.
分析: 要解决此题,需要知道物体漂浮时浮力等于重力.首先根据木块漂浮在水中时的情况计算出木块的密度,后根据木块漂浮在液体中的情况计算出液体的密度.同时此题还要用到阿基米德原理公式F浮=ρ液gV排,而重力G=mg=ρVg.
解答: 解:由ρ=得,m=ρV. 因为木块漂浮在水中,所以F浮水=G木 即ρ水g(1﹣V木)=ρ木V木g 解得ρ木=ρ水=×103kg/m=0.6×103kg/m3 又因为木块在液体中漂浮,所以F浮液=G木 ρ液g(1﹣V木)=ρ木gV木 则ρ液=ρ木=×0.6×103kg/m3=0.8×103kg/m3 故答案为:0.6×103;0.8×103.
5、
考点: 浮力大小的计算;力的合成与应用;阿基米德原理.
专题: 压轴题;动态预测题;推理法.
分析: 分别对铝块、烧杯及水受力分析,根据力的平衡条件得出弹簧测力计示数和台秤示数的表达式,再根据阿基米德原理即可判断铝块逐渐浸入台秤上盛有水的烧杯中、直至刚没入水中两者示数的变化.
解答: 解:(1)对铝块受力分析可知:铝块受竖直向下的重力、竖直向上弹簧测力计的拉力和浮力, 由平衡条件得:G铝=F+F浮,F=G铝﹣F浮, 在铝块完全浸没前,V排逐渐增大,F浮逐渐增大,弹簧测力计的示数F逐渐减小. (2)对烧杯及水受力分析可知:受烧杯及水竖直向下的重力,铝块向下的压力F压=F浮,台秤的支持力FN, 由平衡条件得:台秤的支持力FN=G+F压, 在铝块完全浸没前,V排逐渐增大,F压=F浮逐渐增大,FN逐渐变大,台秤的示数增大. 故选C.
6、
考点: 阿基米德原理.
专题: 浮力.
分析: 绳子拉力是3N,栓在木块下面.那么如果没有绳子,那么浮力等于重力,排水重力是5N. 现在下面有根绳子向下拉了3N,那么要加上3N的水的重力被排开,现在绳子断了, 那么水只排开5N重力的水.少了重力为3N水.求出3牛顿的水的体积是多少,又知道了柱形容器的底面积,体积除以底面积就是水位下降的高度.
解答: 解:绳子受力时木块没入体积为V1,绳子,断后木块没在水中的入体积为V2水面下降h,根根据题意,可得, ρgV1=5N+3N=8N …(1) ρgV2=5N …(2) (1)﹣(2)得绳子断前、断后木块木块没在水中的体积变化量△V, ρg(V1﹣V2)=3N, 则V1﹣V2=3×10﹣4m3, △V=(V1﹣V2)=3×10﹣4m3, ∵V=sh, ∴3×10﹣4m3=h×500×10﹣4m2 ∴h=0.6×10﹣2m. 故选A.
7、
考点: 阿基米德原理.
专题: 计算题;浮力.
分析: 知道甲乙两实心球的质量相同和密度关系,利用密度公式求两球的体积大小关系; 根据两球在水中静止时受到的浮力大小关系确定甲和乙所处的状态(甲下沉、乙漂浮); 甲下沉,受到的浮力F甲=ρ水V甲g;乙漂浮,受到的浮力F乙=m乙g=ρ乙V乙g;根据浮力关系求乙的密度与水的密度关系.
解答: 解:由题知,m甲=m乙, ∵ρ=,ρ甲:ρ乙=3:2, ∴V甲:V乙=2:3; 两球在水中静止时的状态有下面几种情况: ①甲乙都下沉:如果是这样,排开水的体积之比等于V甲:V乙=2:3,由阿基米德原理可知受到的浮力也是2:3,而F甲:F乙=4:5,故①不可行; ②甲乙都漂浮:受到的浮力都等于自重,而两球质量相等、重力相等,受浮力相等,而F甲:F乙=4:5,故②不可行; ③甲漂浮、乙下沉:甲漂浮,F甲=G甲=mg;乙下沉,F乙<G乙=mg,所以F甲>F乙,而F甲:F乙=4:5,故③不可行; ④甲下沉、乙漂浮:甲下沉,F甲<G甲=mg;乙漂浮,F乙=G乙=mg,所以F甲<F乙,而F甲:F乙=4:5,故④可行; 甲下沉,受到的浮力F甲=ρ水V甲g;乙漂浮,受到的浮力F乙=m乙g=ρ乙V乙g; ∵F甲:F乙=4:5, 即ρ水V甲g:ρ乙V乙g=4:5, ρ乙===ρ水. 故选C.
8、
考点: 阿基米德原理.
专题: 浮力.
分析: (1)金属块所受浮力等于物体在空气中的重力减去在水中弹簧秤的拉力(称重法测浮力);已经计算出金属块有的体积浸入水中时所收到的浮力,可利用阿基米德原理F浮=ρgV排计算出金属块全部浸入水中时所受到的浮力; (2)金属块全部浸入水中并碰到杯底,则此时金属块受到竖直向上的支持力、拉力、浮力和竖直向下的重力,则此时测力计的示数为重力减去支持力和浮力.
解答: 解: (1)当金属块体积的三分之一浸入水中静止,此时受到浮力: F浮=G﹣F示=10N﹣8N=2N, 当物体全部浸入水中时,此时排开水的体积等于物体的体积, 此时物体收到的浮力 F浮′=3F浮=3×2N=6N, (2)此时金属块受到竖直向上的支持力、拉力、浮力和竖直向下的重力, ∴此时测力计的示数为:F示′=G﹣F浮′﹣F支持=10N﹣6N﹣F支持=4N﹣F支持. 因此弹簧秤的示数要小于4N,四个选项中D符合题意. 故选D.
9、
考点: 阿基米德原理;力的合成与应用.
专题: 压轴题;推理法;图析法.
分析: 图象可以分成三个过程分析: ①前20s,钢绳的拉力不变,等于物体的重力,此时物体在水面以上; ②中间10s,钢绳的拉力减小,物体从与水面接触到完全浸没; ③最后90s,钢绳的拉力不变,此时物体完全浸没在水中.
解答: 解: A、由图象可以看出,物体在第20s开始浸入水中.此选项正确,不符合题意; B、在前20s,物体的重力等于受到的拉力为1400N.此选项正确,不符合题意; C、在第20s~30s的过程中,物体排开水的体积不断增大,由公式F浮=ρ液gV排知,浮力不断增大.此选项错误,符合题意; D、石料完全浸没后,浮力不变,钢绳的拉力不变,始终为900N.此选项正确,不符合题意. 故选C.
拓展题
考点: 浮力大小的计算;密度公式的应用;物体的浮沉条件及其应用.
解析: 根据ρ=可得: V排=V溢===50cm3, G排=m排g=50×10﹣3kg×10N/kg=0.5N; 轻轻放入小球后,有三种情况: (1)漂浮: ∵F浮=G排=G球=0.5N ∴m排=m球=50g,V>50cm3,ρ=<=1.0g/cm3; (2)悬浮: ∵F浮=G排=G球=0.5N ∴m排=m球=50g,V=50cm3,ρ===1.0g/cm3; (3)下沉: ∵F浮=G排=0.5N<G球, ∴m球>m排=50g,V=50cm3,ρ=>=1.0g/cm3; 可见:F浮=0.5N,m球≥50g,V≥50cm3,ρ可能大于1.0g/cm3,可能等于1.0g/cm3,可能小于1.0g/cm3.
答案: D
考点: 阿基米德原理;力的合成与应用.
解析: 已知m甲=m乙,则G甲=G乙;ρ甲=0.8×103kg/m3,ρ乙=0.4×103kg/m3, 由m=ρV得:====1,则V乙=2V甲, 浮力F浮=ρgV排,则==,F乙浮=2F甲浮, ===,F甲浮=G甲, ===,F乙浮=G乙=G甲, 甲受重力G甲、浮力F甲浮、弹簧的拉力F甲拉处于平衡状态,G甲+F甲拉=F甲浮,F甲拉=F甲浮﹣G甲=G甲﹣G甲=G甲, 甲受重力G乙、浮力F乙浮、拉力F乙拉处于平衡状态,G乙+F乙拉=F乙浮,F乙拉=F乙浮﹣G乙=G乙﹣G乙=G乙=G甲, ==.
答案: BC
(
1
)
同课章节目录
