人教版数学九下 28.1锐角三角函数(3)课件(23张ppt)
文档属性
| 名称 | 人教版数学九下 28.1锐角三角函数(3)课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 521.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-23 00:00:00 | ||
图片预览





文档简介
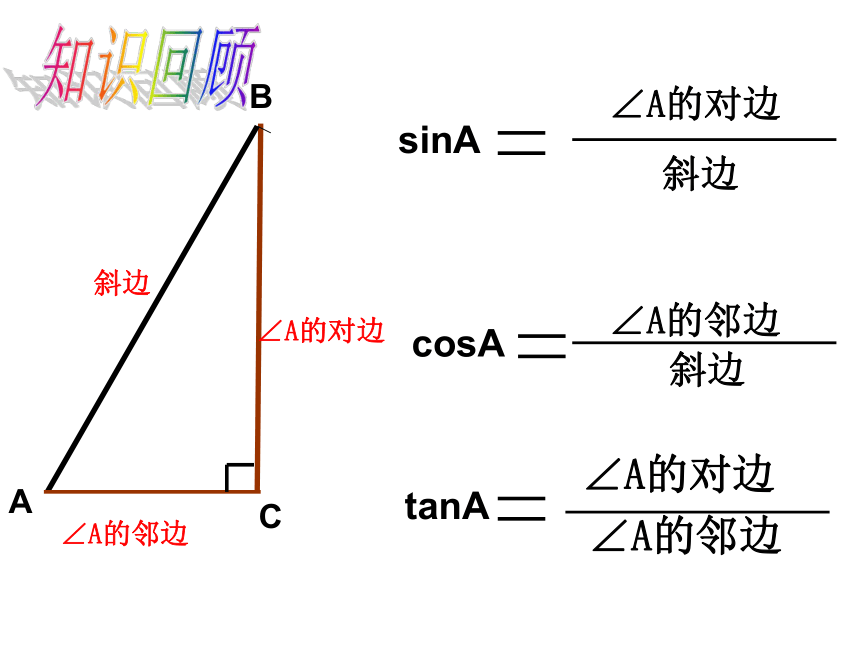
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。
① a=9 b=12
② a=6 b=8
1、掌握 30°、45°、60°角的三角函数值,能够用它们进行计算;
2、能够根据30°、45°、60°角的三角函数值,说出相应锐角的大小。
自主学习课本65----66页
尝试计算30°、45°、60°
角的三角函数值
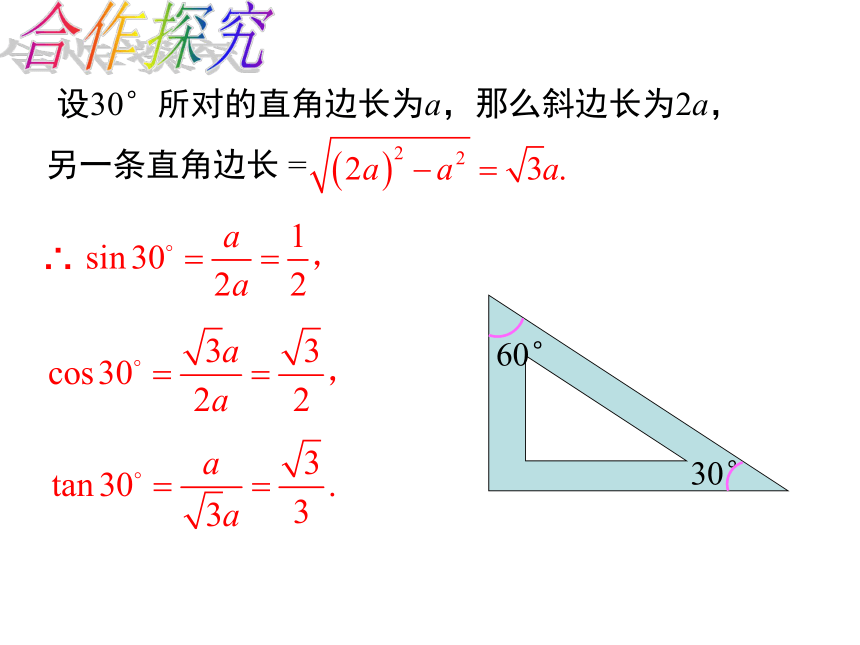
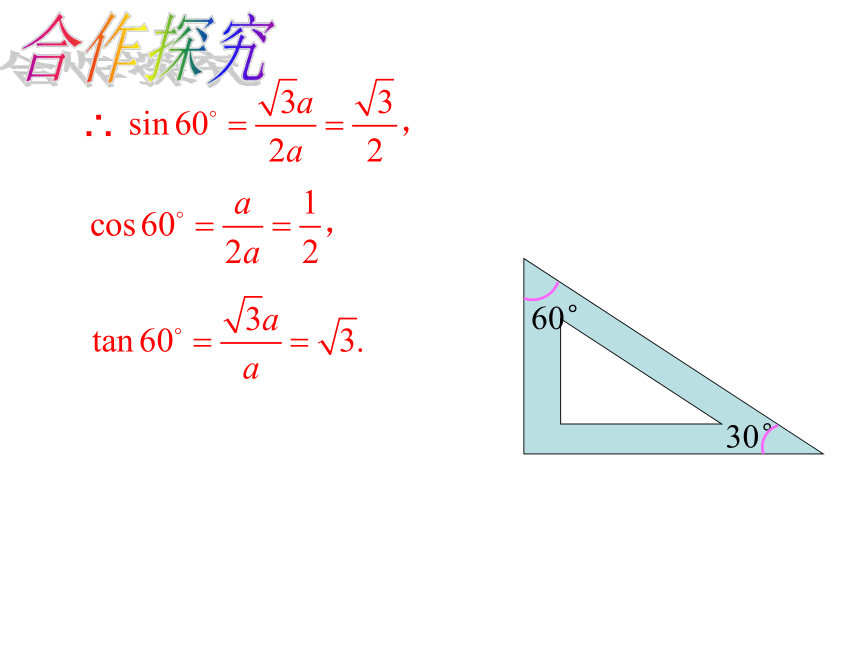
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
设两条直角边长为 a,则斜边长 =
三角函数
锐角α
特殊角三角函数值
30° 45° 60°
sinα
cosα
tanα
例3、求下列各式的值.
(1) cos260°+sin260°
1、计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解: 在图中,
∴ ∠A = 45°.
解: 在图中,
∴ α = 60°.
∴ tanB= ,sinA=
∴ ∠B=60°,∠A=60°.
2、已知:| tanB- | + (2 sinA- )2 =0,
求∠A,∠B的度数.
本节课你学习了什么知识?
上交作业:课本第67页第1、2题 .
课后作业:报纸1-5.
2、已知:α为锐角,且满足 ,求α的度数。
3、在Rt△ABC中,∠C=90°,化简
4、操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。
① a=9 b=12
② a=6 b=8
1、掌握 30°、45°、60°角的三角函数值,能够用它们进行计算;
2、能够根据30°、45°、60°角的三角函数值,说出相应锐角的大小。
自主学习课本65----66页
尝试计算30°、45°、60°
角的三角函数值
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
设两条直角边长为 a,则斜边长 =
三角函数
锐角α
特殊角三角函数值
30° 45° 60°
sinα
cosα
tanα
例3、求下列各式的值.
(1) cos260°+sin260°
1、计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解: 在图中,
∴ ∠A = 45°.
解: 在图中,
∴ α = 60°.
∴ tanB= ,sinA=
∴ ∠B=60°,∠A=60°.
2、已知:| tanB- | + (2 sinA- )2 =0,
求∠A,∠B的度数.
本节课你学习了什么知识?
上交作业:课本第67页第1、2题 .
课后作业:报纸1-5.
2、已知:α为锐角,且满足 ,求α的度数。
3、在Rt△ABC中,∠C=90°,化简
4、操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
