江苏省高邮市2018-2019学年度第二学期高一期中数学调研试卷含答案
文档属性
| 名称 | 江苏省高邮市2018-2019学年度第二学期高一期中数学调研试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-24 09:22:55 | ||
图片预览




文档简介
高邮市2019年高一年级阶段性学情调研
数学试题 2019.04
一、选择题(本大题共10小题,每小题5分,共计50分)
1.在中,角A,B,C的对边分别为a,b,c,,则﹙ ﹚
A. B. C. D.
2.垂直于同一条直线的两条直线一定﹙ ﹚
A.平行 B.相交 C.异面 D.以上都有可能
3.在中,角A,B,C的对边分别为a,b,c,如果,那么等于﹙ ﹚
A. B. C. D.
4.若球的体积与其表面积的数值相等,则球的半径为﹙ ﹚
A.1 B.3 C.2 D.
5.下列命题中,正确命题的个数为﹙ ﹚
(1)首尾相接的四条线段在同一平面内 (2)三条互相平行的线段在同一平面内
(3)两两相交的四条直线在同一个平面内
(4)若四个点中的三个点在同一直线上,那么这四个点在同一平面内.
A.1 B.2 C.3 D.4
6. 根据下列情况,判断三角形解的情况,其中正确的是﹙ ﹚
A.,有两解 B.,有一解
C.,无解 D.,有一解
7.已知正四面体(所有面为正三角形)中,是的中点,则异面直线与所成角的
余弦值为﹙ ﹚
A. B. C. D.
8.设是两条不同的直线,是三个不同的平面,给出下面四个命题:
(1)若,则 (2)若,则
(3)若,则 (4)若,则
其中正确命题个数是﹙ ﹚
A.1 B. 2 C.3 D. 4
9.在△ABC中,角A,B,C的对边分别为a,b,c,,,且,则的形状是﹙ ﹚
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等腰或直角三角形
10.在锐角中,角、、的对边分别为、、,若,则的取值范围是﹙ ﹚
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共计30分)
11.长方体中,,则与平面所成的角的大小为 ▲ .
12.已知圆锥的侧面展开图是一个半径为,圆心角为的扇形,则此圆锥的高为 ▲ .
13.如图,一艘船上午在A处测得灯塔在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午到达处,此时又测得灯塔在它的北偏东75°处,且与它相距海里,此船的航速为 ▲ 海里小时.
14.在正方体中,给出以下四个结论:
(1)直线平面;(2)直线与平面相交;
(3)直线平面; (4)平面平面.
上述结论中,所有正确结论的序号为 ▲ .
15.在△中,已知,边上的中线,则的值为 ▲ .
16.在中,内角所对的边分别为.已知,,,设的面积为,,则的最小值为 ▲ .
三、解答题(本大题共6小题,共计70分。解答时,要写出必要的解题过程及步骤)
17.(本小题满分10分)如图,在四棱锥S﹣ABCD中,底面ABCD为菱形,平面ABCD.
(1)求证://平面;
(2)求证:.
18. (本小题满分12分)的内角的对边为,
(1)求;
(2)若求.
19.(本小题满分12分)三棱柱ABC﹣A1B1C1被平面A1B1C截去一部分后得到如图所示几何体,BB1⊥平面ABC,∠ABC=90°,BC=BB1,E为棱B1C上的动点(不包含端点),平面ABE交A1C于点F.
(1)求证:EF//AB;
(2)若点E为中点,求证:平面ABE⊥平面A1B1C.
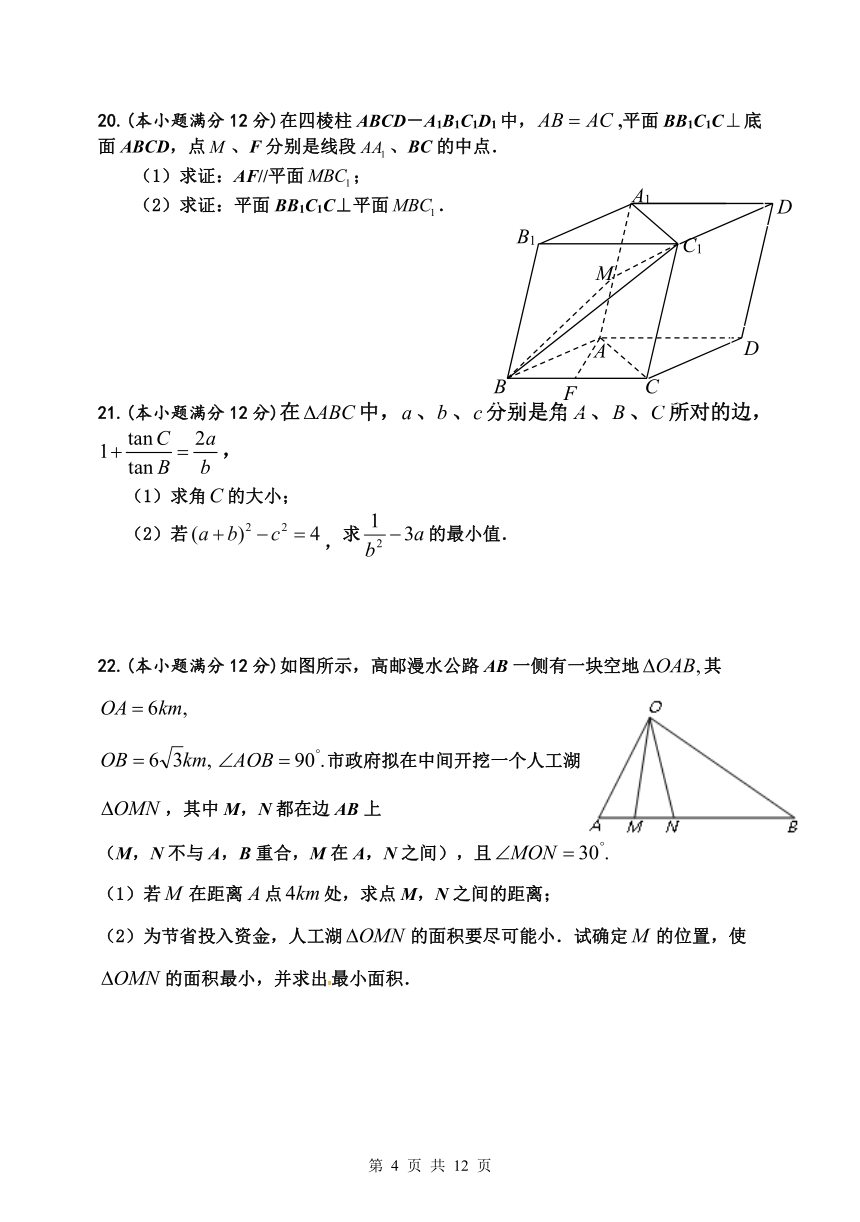
20.(本小题满分12分)在四棱柱ABCD-A1B1C1D1中,,平面BB1C1C底面ABCD,点、F分别是线段、BC的中点.
(1)求证:AF//平面;
(2)求证:平面BB1C1C⊥平面.
21.(本小题满分12分)在中,、、分别是角、、所对的边,,
(1)求角的大小;
(2)若,求的最小值.
22.(本小题满分12分)如图所示,高邮漫水公路AB一侧有一块空地其
市政府拟在中间开挖一个人工湖,其中M,N都在边AB上
(M,N不与A,B重合,M在A,N之间),且
(1)若在距离点处,求点M,N之间的距离;
(2)为节省投入资金,人工湖的面积要尽可能小.试确定的位置,使的面积最小,并求出最小面积.
2019年高一年级阶段性学情调研 2019.4
高 一 数 学 参 考 答 案
1. A 2.D 3.B 4. B 5. A 6. D 7.B 8. A 9.D 10.D
11. 12. 13. 14. 15. 16.
17. 证:(1)在四棱锥中,底面为菱形
所以, ……2分
……4分
(2)连结.
……6分
,
……9分
……10分
18. 解:(1)由正弦定理,得 ……2分
由余弦定理,得,又
所以 ……4分
(2) 由(1)知:,又
所以,又 ……6分
根据正弦定理,得
……9分
所以 ……12分
19. 证:(1)在三棱柱中,
是平行四边形
……2分
又
……4分
(2)
……6分
,又 ……8分
由(1)知:
点为的中点
……10分
,
,
. ……12分
20. (1)方法一:取中点,连
分别为中点
……2分
为四棱柱
又为的中点,
……4分
又
……6分
方法二:取中点,连
又
……2分
又是四棱柱
……4分
又
又
又
……6分
(2)
又,
……8分
又
而
……10分
又
又
……12分
21. 由正弦定理得:
……2分
……4分
……6分
又 ……8分
,当时, ……12分
22. 解:(1)中,
则 ……2分
中,
所以 ……4分
(2)方法一:设
在中,
则
所以
又中,所以
所以 ……7分
所以
……9分
令
利用的单调性解得,当即时取得最小值,此时面积取得最小值,最小值为
答:当时,的面积最小,最小值为。 ……12分
方法二:设
在中,得
在中,得 ……6分
……9分
因为 所以当时面积最小,最小值为
此时中,则
答:当时,的面积最小,最小值为。 ……12分
B
A
B1
A1
C1
M
C
F
D
D1
数学试题 2019.04
一、选择题(本大题共10小题,每小题5分,共计50分)
1.在中,角A,B,C的对边分别为a,b,c,,则﹙ ﹚
A. B. C. D.
2.垂直于同一条直线的两条直线一定﹙ ﹚
A.平行 B.相交 C.异面 D.以上都有可能
3.在中,角A,B,C的对边分别为a,b,c,如果,那么等于﹙ ﹚
A. B. C. D.
4.若球的体积与其表面积的数值相等,则球的半径为﹙ ﹚
A.1 B.3 C.2 D.
5.下列命题中,正确命题的个数为﹙ ﹚
(1)首尾相接的四条线段在同一平面内 (2)三条互相平行的线段在同一平面内
(3)两两相交的四条直线在同一个平面内
(4)若四个点中的三个点在同一直线上,那么这四个点在同一平面内.
A.1 B.2 C.3 D.4
6. 根据下列情况,判断三角形解的情况,其中正确的是﹙ ﹚
A.,有两解 B.,有一解
C.,无解 D.,有一解
7.已知正四面体(所有面为正三角形)中,是的中点,则异面直线与所成角的
余弦值为﹙ ﹚
A. B. C. D.
8.设是两条不同的直线,是三个不同的平面,给出下面四个命题:
(1)若,则 (2)若,则
(3)若,则 (4)若,则
其中正确命题个数是﹙ ﹚
A.1 B. 2 C.3 D. 4
9.在△ABC中,角A,B,C的对边分别为a,b,c,,,且,则的形状是﹙ ﹚
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等腰或直角三角形
10.在锐角中,角、、的对边分别为、、,若,则的取值范围是﹙ ﹚
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共计30分)
11.长方体中,,则与平面所成的角的大小为 ▲ .
12.已知圆锥的侧面展开图是一个半径为,圆心角为的扇形,则此圆锥的高为 ▲ .
13.如图,一艘船上午在A处测得灯塔在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午到达处,此时又测得灯塔在它的北偏东75°处,且与它相距海里,此船的航速为 ▲ 海里小时.
14.在正方体中,给出以下四个结论:
(1)直线平面;(2)直线与平面相交;
(3)直线平面; (4)平面平面.
上述结论中,所有正确结论的序号为 ▲ .
15.在△中,已知,边上的中线,则的值为 ▲ .
16.在中,内角所对的边分别为.已知,,,设的面积为,,则的最小值为 ▲ .
三、解答题(本大题共6小题,共计70分。解答时,要写出必要的解题过程及步骤)
17.(本小题满分10分)如图,在四棱锥S﹣ABCD中,底面ABCD为菱形,平面ABCD.
(1)求证://平面;
(2)求证:.
18. (本小题满分12分)的内角的对边为,
(1)求;
(2)若求.
19.(本小题满分12分)三棱柱ABC﹣A1B1C1被平面A1B1C截去一部分后得到如图所示几何体,BB1⊥平面ABC,∠ABC=90°,BC=BB1,E为棱B1C上的动点(不包含端点),平面ABE交A1C于点F.
(1)求证:EF//AB;
(2)若点E为中点,求证:平面ABE⊥平面A1B1C.
20.(本小题满分12分)在四棱柱ABCD-A1B1C1D1中,,平面BB1C1C底面ABCD,点、F分别是线段、BC的中点.
(1)求证:AF//平面;
(2)求证:平面BB1C1C⊥平面.
21.(本小题满分12分)在中,、、分别是角、、所对的边,,
(1)求角的大小;
(2)若,求的最小值.
22.(本小题满分12分)如图所示,高邮漫水公路AB一侧有一块空地其
市政府拟在中间开挖一个人工湖,其中M,N都在边AB上
(M,N不与A,B重合,M在A,N之间),且
(1)若在距离点处,求点M,N之间的距离;
(2)为节省投入资金,人工湖的面积要尽可能小.试确定的位置,使的面积最小,并求出最小面积.
2019年高一年级阶段性学情调研 2019.4
高 一 数 学 参 考 答 案
1. A 2.D 3.B 4. B 5. A 6. D 7.B 8. A 9.D 10.D
11. 12. 13. 14. 15. 16.
17. 证:(1)在四棱锥中,底面为菱形
所以, ……2分
……4分
(2)连结.
……6分
,
……9分
……10分
18. 解:(1)由正弦定理,得 ……2分
由余弦定理,得,又
所以 ……4分
(2) 由(1)知:,又
所以,又 ……6分
根据正弦定理,得
……9分
所以 ……12分
19. 证:(1)在三棱柱中,
是平行四边形
……2分
又
……4分
(2)
……6分
,又 ……8分
由(1)知:
点为的中点
……10分
,
,
. ……12分
20. (1)方法一:取中点,连
分别为中点
……2分
为四棱柱
又为的中点,
……4分
又
……6分
方法二:取中点,连
又
……2分
又是四棱柱
……4分
又
又
又
……6分
(2)
又,
……8分
又
而
……10分
又
又
……12分
21. 由正弦定理得:
……2分
……4分
……6分
又 ……8分
,当时, ……12分
22. 解:(1)中,
则 ……2分
中,
所以 ……4分
(2)方法一:设
在中,
则
所以
又中,所以
所以 ……7分
所以
……9分
令
利用的单调性解得,当即时取得最小值,此时面积取得最小值,最小值为
答:当时,的面积最小,最小值为。 ……12分
方法二:设
在中,得
在中,得 ……6分
……9分
因为 所以当时面积最小,最小值为
此时中,则
答:当时,的面积最小,最小值为。 ……12分
B
A
B1
A1
C1
M
C
F
D
D1
同课章节目录
