八年级数学下册 18.2.1 矩形的性质课件(共32张PPT)
文档属性
| 名称 | 八年级数学下册 18.2.1 矩形的性质课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-24 00:00:00 | ||
图片预览






文档简介
课件32张PPT。18.2.1矩形(1)导入新课1.什么叫平行四边形?2.平行四边形有哪些性质?
①边:
②角:
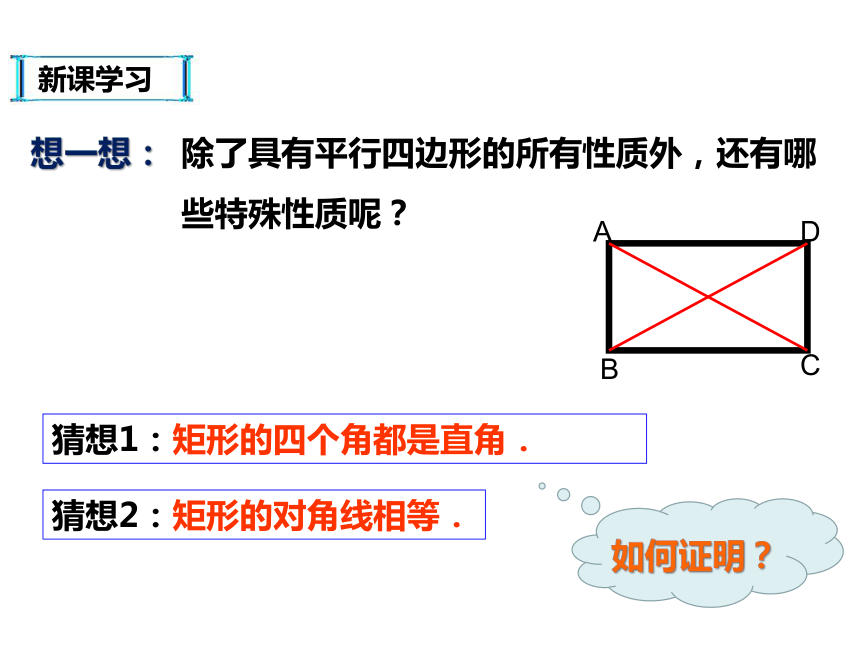
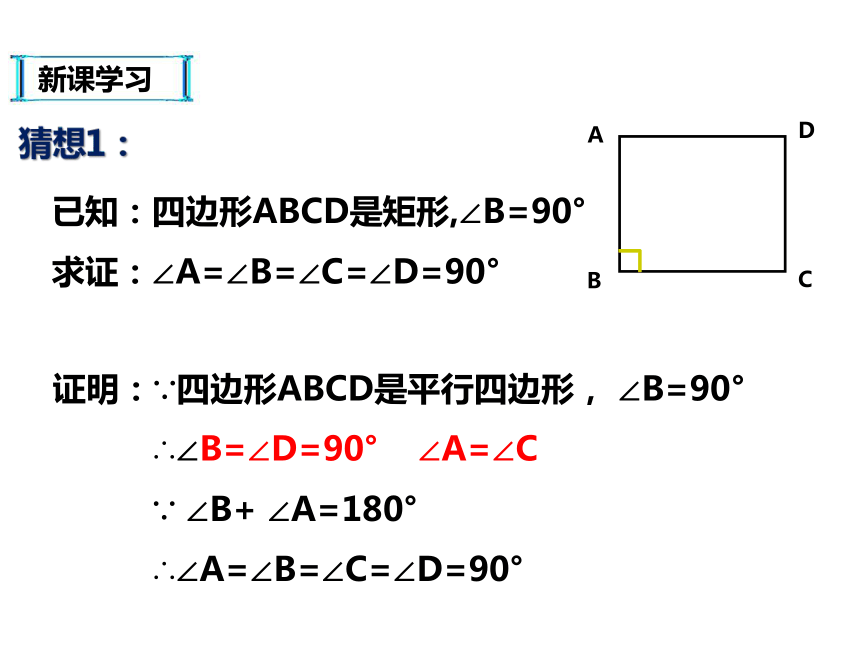
③对角线:对边平行且相等.对角相等且邻角互补.互相平分.两组对边分别平行的四边形叫做平行四边形。 导入新课特殊的平行四边形新课学习矩形的性质有一个角是直角的平行四边形叫做矩形。新课学习新课学习四、矩形的两条对角线互相平分;三、矩形的两组对角分别相等;二、矩形的两组对边分别相等;五、矩形的邻角互补。矩形的性质1:一、矩形的两组对边分别平行;新课学习想一想:猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD除了具有平行四边形的所有性质外,还有哪些特殊性质呢?如何证明?新课学习已知:四边形ABCD是矩形,∠B=90°
求证:∠A=∠B=∠C=∠D=90°DCBA证明:∵四边形ABCD是平行四边形, ∠B=90°
∴∠B=∠D=90° ∠A=∠C
∵ ∠B+ ∠A=180°
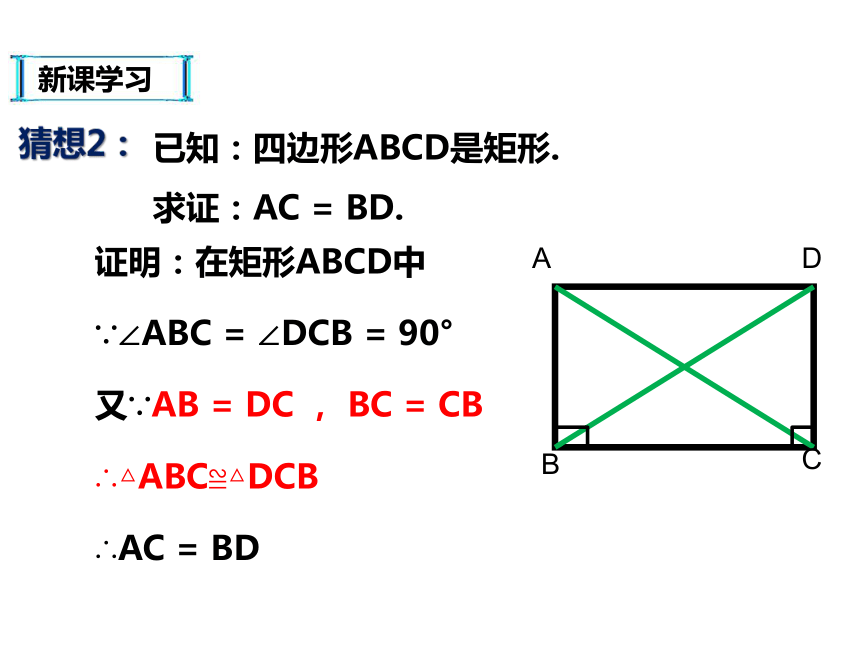
∴∠A=∠B=∠C=∠D=90°猜想1:新课学习已知:四边形ABCD是矩形.
求证:AC = BD.证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD猜想2:新课学习 ∵ 四边形ABCD是矩形,
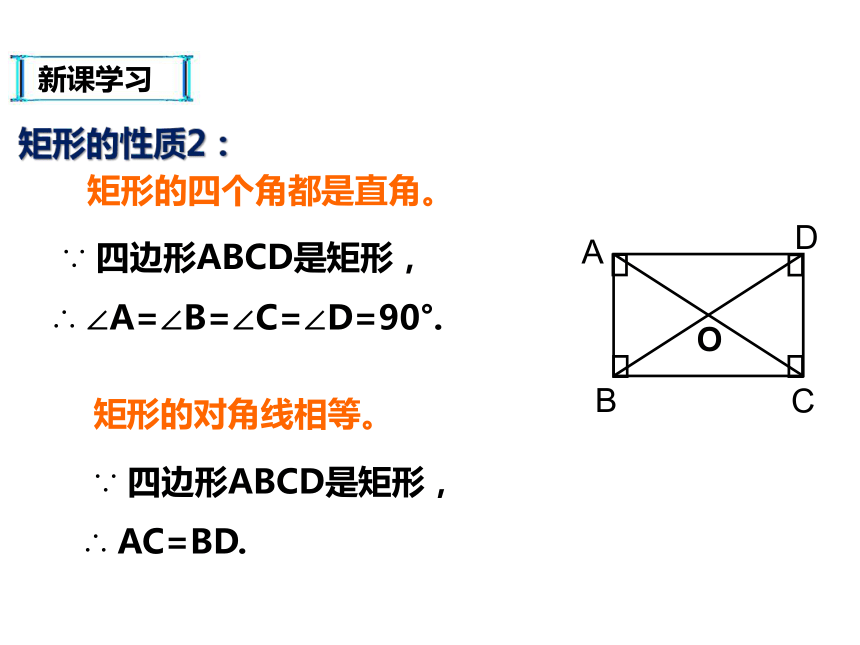
∴ ∠A=∠B=∠C=∠D=90°.矩形的四个角都是直角。矩形的对角线相等。ABCDO ∵ 四边形ABCD是矩形,
∴ AC=BD.矩形的性质2:新课学习矩形的性质对边平行且相等对角相等,邻角互补对角线互相平分对边平行且相等对角相等,邻角互补对角线互相平分没什么特别的四个角都是直角对角线相等知识巩固1.长方形ABCD中,AB=8,对角线AC=10,求矩形ABCD的面积。分析:矩形各内角为直角,已知AC,AB,根据勾股定理即可求得BC的值,根据AB,BC即可求得矩形ABCD的面积知识巩固?知识巩固2.如图,在矩形ABCD中,两对角线相交于点O,AE⊥BD于E,若∠DAE=3∠BAE,求∠OAE与∠DAO的度数。分析:根据矩形性质求出OA=OB,∠BAD=90°,求出∠BAE=22.5°,∠DAE=67.5°,求出∠ABO的度数和推出∠OAB=∠OBA,即可求出答案。知识巩固?新课学习 如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论? Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?一般地,这个结论对所有直角三角形都成立吗? 探究 直角三角形新课学习 AC=BD??新课学习OCDAB┛直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。?新课学习例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,
AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分,∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝)
∴ 矩形的对角线长
AC=BD=2OA=8(㎝)O 方法小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.新课学习变式1:如图,矩形ABCD的对角线AC、BD相交于点O,∠BOC=120°,AB=4cm,则AC= .
变式2:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB:∠BOC=1:2 ,AB=4cm,则AC= .
变式3:如图,矩形ABCD的ABCD的对角线AC、BD相交于点O,∠AOB=60°,AC=8,则AB=_____.
8cm8cm4cm知识巩固3.如图,在四边形ABCD中,∠BAD=∠BCD=90°,O是BD中点,E是AC中点,试说明OE⊥AC。知识巩固?知识巩固4.已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点。
求证:GF⊥DE。知识巩固?课堂小结 直角三角形斜边上的中线等于斜边的一半。矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分。矩形:有一个角是直角的平行四边形叫做矩形。达标检测1.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )
A.3、5 B.4、5 C.3、4 D.4、3?D达标检测2.已知矩形ABCD中,对角线AC=10,周长为28,则矩形的面积为 .
分析:设长方形的长为x、宽为y,根据长方形的周长可以计算x+y的值,根据勾股定理即可列出关于x、y的方程式,即可求得x、y的值.48达标检测3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A.60° B.45° C.30° D.75°
分析:根据轴对称的性质可知∠CED=∠A,根据直角三角形斜边上的中线的性质、等腰三角形的性质可得∠ECA=∠A,∠B=∠BCE,根据等边三角形的判定和性质可得∠CED=60°,再根据三角形外角的性质可得∠B的度数,从而求得答案.C达标检测4.如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH。
达标检测?拓展提升1.如图所示.矩形ABCD中,CE⊥BD于E,AF平分∠BAD交EC延长线于F.求证:CA=CF分析:只要证明△CAF是等腰三角形,即∠CAF=∠CFA即可.由于∠CAF=45°-∠CAD,所以,在添加辅助线时,应设法产生一个与∠CAD相等的角a,使得∠CFA=45°-a.为此,延长DC交AF于H,并设AF与BC交于G,我们不难证明∠FCH=∠CAD.拓展提升解析:延长DC交AF于H,显然∠FCH=∠DCE.
又在Rt△BCD中,由于CE⊥BD,故∠DCE=∠DBC.
∵矩形对角线相等,
∴△DCB≌△CDA,从而∠DBC=∠CAD,
∴∠FCH=∠CAD①
又∵ AG平分∠BAD=90°,
∴△ABG是等腰直角三角形,
从而易证△HCG也是等腰直角三角形,所以∠CHG=45°.
∵ ∠CHG是△CHF的外角,∴∠CHG=∠CFH+∠FCH=45°,
∴∠CFH=45°-∠FCH②
由①,②∠CFH=45°-∠CAD=∠CAF,于是在三角形CAF中,有CA=CF。
①边:
②角:
③对角线:对边平行且相等.对角相等且邻角互补.互相平分.两组对边分别平行的四边形叫做平行四边形。 导入新课特殊的平行四边形新课学习矩形的性质有一个角是直角的平行四边形叫做矩形。新课学习新课学习四、矩形的两条对角线互相平分;三、矩形的两组对角分别相等;二、矩形的两组对边分别相等;五、矩形的邻角互补。矩形的性质1:一、矩形的两组对边分别平行;新课学习想一想:猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD除了具有平行四边形的所有性质外,还有哪些特殊性质呢?如何证明?新课学习已知:四边形ABCD是矩形,∠B=90°
求证:∠A=∠B=∠C=∠D=90°DCBA证明:∵四边形ABCD是平行四边形, ∠B=90°
∴∠B=∠D=90° ∠A=∠C
∵ ∠B+ ∠A=180°
∴∠A=∠B=∠C=∠D=90°猜想1:新课学习已知:四边形ABCD是矩形.
求证:AC = BD.证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD猜想2:新课学习 ∵ 四边形ABCD是矩形,
∴ ∠A=∠B=∠C=∠D=90°.矩形的四个角都是直角。矩形的对角线相等。ABCDO ∵ 四边形ABCD是矩形,
∴ AC=BD.矩形的性质2:新课学习矩形的性质对边平行且相等对角相等,邻角互补对角线互相平分对边平行且相等对角相等,邻角互补对角线互相平分没什么特别的四个角都是直角对角线相等知识巩固1.长方形ABCD中,AB=8,对角线AC=10,求矩形ABCD的面积。分析:矩形各内角为直角,已知AC,AB,根据勾股定理即可求得BC的值,根据AB,BC即可求得矩形ABCD的面积知识巩固?知识巩固2.如图,在矩形ABCD中,两对角线相交于点O,AE⊥BD于E,若∠DAE=3∠BAE,求∠OAE与∠DAO的度数。分析:根据矩形性质求出OA=OB,∠BAD=90°,求出∠BAE=22.5°,∠DAE=67.5°,求出∠ABO的度数和推出∠OAB=∠OBA,即可求出答案。知识巩固?新课学习 如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论? Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?一般地,这个结论对所有直角三角形都成立吗? 探究 直角三角形新课学习 AC=BD??新课学习OCDAB┛直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。?新课学习例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,
AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分,∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝)
∴ 矩形的对角线长
AC=BD=2OA=8(㎝)O 方法小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.新课学习变式1:如图,矩形ABCD的对角线AC、BD相交于点O,∠BOC=120°,AB=4cm,则AC= .
变式2:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB:∠BOC=1:2 ,AB=4cm,则AC= .
变式3:如图,矩形ABCD的ABCD的对角线AC、BD相交于点O,∠AOB=60°,AC=8,则AB=_____.
8cm8cm4cm知识巩固3.如图,在四边形ABCD中,∠BAD=∠BCD=90°,O是BD中点,E是AC中点,试说明OE⊥AC。知识巩固?知识巩固4.已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点。
求证:GF⊥DE。知识巩固?课堂小结 直角三角形斜边上的中线等于斜边的一半。矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分。矩形:有一个角是直角的平行四边形叫做矩形。达标检测1.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )
A.3、5 B.4、5 C.3、4 D.4、3?D达标检测2.已知矩形ABCD中,对角线AC=10,周长为28,则矩形的面积为 .
分析:设长方形的长为x、宽为y,根据长方形的周长可以计算x+y的值,根据勾股定理即可列出关于x、y的方程式,即可求得x、y的值.48达标检测3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A.60° B.45° C.30° D.75°
分析:根据轴对称的性质可知∠CED=∠A,根据直角三角形斜边上的中线的性质、等腰三角形的性质可得∠ECA=∠A,∠B=∠BCE,根据等边三角形的判定和性质可得∠CED=60°,再根据三角形外角的性质可得∠B的度数,从而求得答案.C达标检测4.如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH。
达标检测?拓展提升1.如图所示.矩形ABCD中,CE⊥BD于E,AF平分∠BAD交EC延长线于F.求证:CA=CF分析:只要证明△CAF是等腰三角形,即∠CAF=∠CFA即可.由于∠CAF=45°-∠CAD,所以,在添加辅助线时,应设法产生一个与∠CAD相等的角a,使得∠CFA=45°-a.为此,延长DC交AF于H,并设AF与BC交于G,我们不难证明∠FCH=∠CAD.拓展提升解析:延长DC交AF于H,显然∠FCH=∠DCE.
又在Rt△BCD中,由于CE⊥BD,故∠DCE=∠DBC.
∵矩形对角线相等,
∴△DCB≌△CDA,从而∠DBC=∠CAD,
∴∠FCH=∠CAD①
又∵ AG平分∠BAD=90°,
∴△ABG是等腰直角三角形,
从而易证△HCG也是等腰直角三角形,所以∠CHG=45°.
∵ ∠CHG是△CHF的外角,∴∠CHG=∠CFH+∠FCH=45°,
∴∠CFH=45°-∠FCH②
由①,②∠CFH=45°-∠CAD=∠CAF,于是在三角形CAF中,有CA=CF。
