青岛版六年级数学下册三单元比例知识整理和复习(16页PPT)
文档属性
| 名称 | 青岛版六年级数学下册三单元比例知识整理和复习(16页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-25 00:00:00 | ||
图片预览





文档简介
整
理
和
复
习
青岛版六年级数学下册第三单元
三单元 比、比例
山东滨州沾化大高镇第二小学
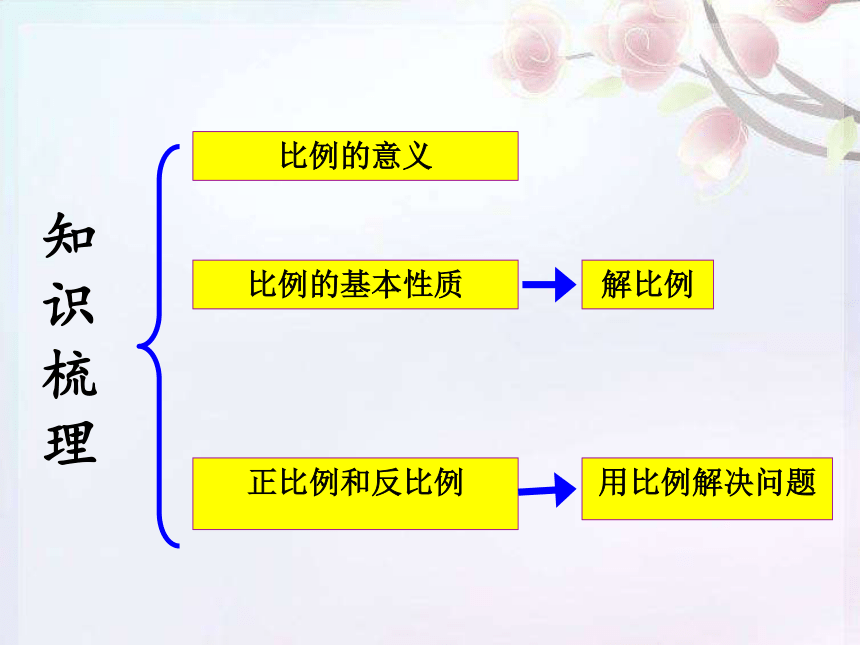
比例的意义
比例的基本性质
正比例和反比例
用比例解决问题
知
识
梳
理
解比例
复习目标
1.理解比例的意义和基本性质,
会解比例。
3.能够正确判断正、反比例的量,
会用比例的知识解决简单的实际问题。
2.理解正、反比例的意义,
初步认识正、反比例图像。
1、什么叫做比?
两个数相除又叫做两个数的比。
2、什么叫做比例?
表示两个比相等的式子叫做比例。
比例的意义
1、比的基本性质是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、比例的基本性质是什么?
在比例里,两个内项的积等于两个外项的积。
3、比和比例有什么区别和联系?
比例的基本性质
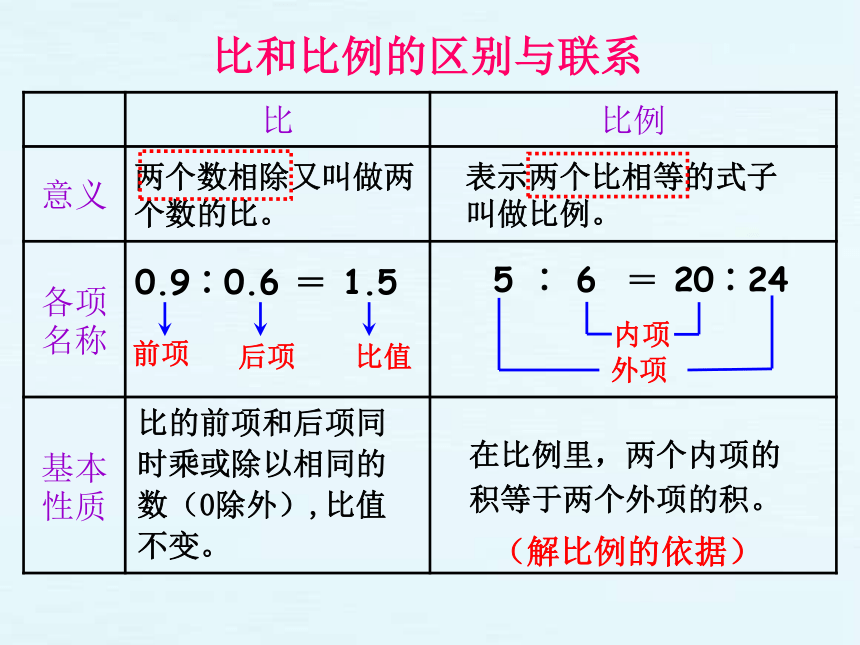
比和比例的区别与联系
两个数相除又叫做两
个数的比。
表示两个比相等的式子
叫做比例。
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
(解比例的依据)
比 比例
意义
各项名称
基本性质
1、什么叫解比例?依据是什么?
求比例中的未知项叫做解比例。
解比例的依据是比例的基本性质。
解比例
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的比值(也就是商)一定,
这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
关系式:
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的积一定,
这两种量就叫做成反比例的量,
它们的关系叫做反比例关系。
关系式:
什么叫正比例关系?什么叫反比例关系?
正、反比例的相同点和不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1、变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2、相关联的两个量相对应的两个数的比值(商)一定。
2、相关联的两个量相对应的两个数的乘积一定。
3、关系式:
3、关系式:
正比例 反比例
相同点
不同点
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商(比值)一定
→成反比例
→成正比例
正比例和反比例
除数和商是两种相关联的量,因为除数×商=被除数(一定),所以除数和商成反比例。
1、判断题目中两种相关联的量是成正比例还是反比例;
2、设未知量为x,注意写明计量单位;
3、列出比例式,并解比例式;
4、检查后写出答案;
5、特别注意所得答案是否符合实际
解比例应用题的一般方法和步骤:
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
用比例解决问题
解:设返回时用了X小时。
答:返回时用了2.5小时。
理
和
复
习
青岛版六年级数学下册第三单元
三单元 比、比例
山东滨州沾化大高镇第二小学
比例的意义
比例的基本性质
正比例和反比例
用比例解决问题
知
识
梳
理
解比例
复习目标
1.理解比例的意义和基本性质,
会解比例。
3.能够正确判断正、反比例的量,
会用比例的知识解决简单的实际问题。
2.理解正、反比例的意义,
初步认识正、反比例图像。
1、什么叫做比?
两个数相除又叫做两个数的比。
2、什么叫做比例?
表示两个比相等的式子叫做比例。
比例的意义
1、比的基本性质是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、比例的基本性质是什么?
在比例里,两个内项的积等于两个外项的积。
3、比和比例有什么区别和联系?
比例的基本性质
比和比例的区别与联系
两个数相除又叫做两
个数的比。
表示两个比相等的式子
叫做比例。
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
(解比例的依据)
比 比例
意义
各项名称
基本性质
1、什么叫解比例?依据是什么?
求比例中的未知项叫做解比例。
解比例的依据是比例的基本性质。
解比例
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的比值(也就是商)一定,
这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
关系式:
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的积一定,
这两种量就叫做成反比例的量,
它们的关系叫做反比例关系。
关系式:
什么叫正比例关系?什么叫反比例关系?
正、反比例的相同点和不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1、变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2、相关联的两个量相对应的两个数的比值(商)一定。
2、相关联的两个量相对应的两个数的乘积一定。
3、关系式:
3、关系式:
正比例 反比例
相同点
不同点
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商(比值)一定
→成反比例
→成正比例
正比例和反比例
除数和商是两种相关联的量,因为除数×商=被除数(一定),所以除数和商成反比例。
1、判断题目中两种相关联的量是成正比例还是反比例;
2、设未知量为x,注意写明计量单位;
3、列出比例式,并解比例式;
4、检查后写出答案;
5、特别注意所得答案是否符合实际
解比例应用题的一般方法和步骤:
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
用比例解决问题
解:设返回时用了X小时。
答:返回时用了2.5小时。
