江苏省溧水高级中学2018-2019学年高二下学期期中考试 数学
文档属性
| 名称 | 江苏省溧水高级中学2018-2019学年高二下学期期中考试 数学 | 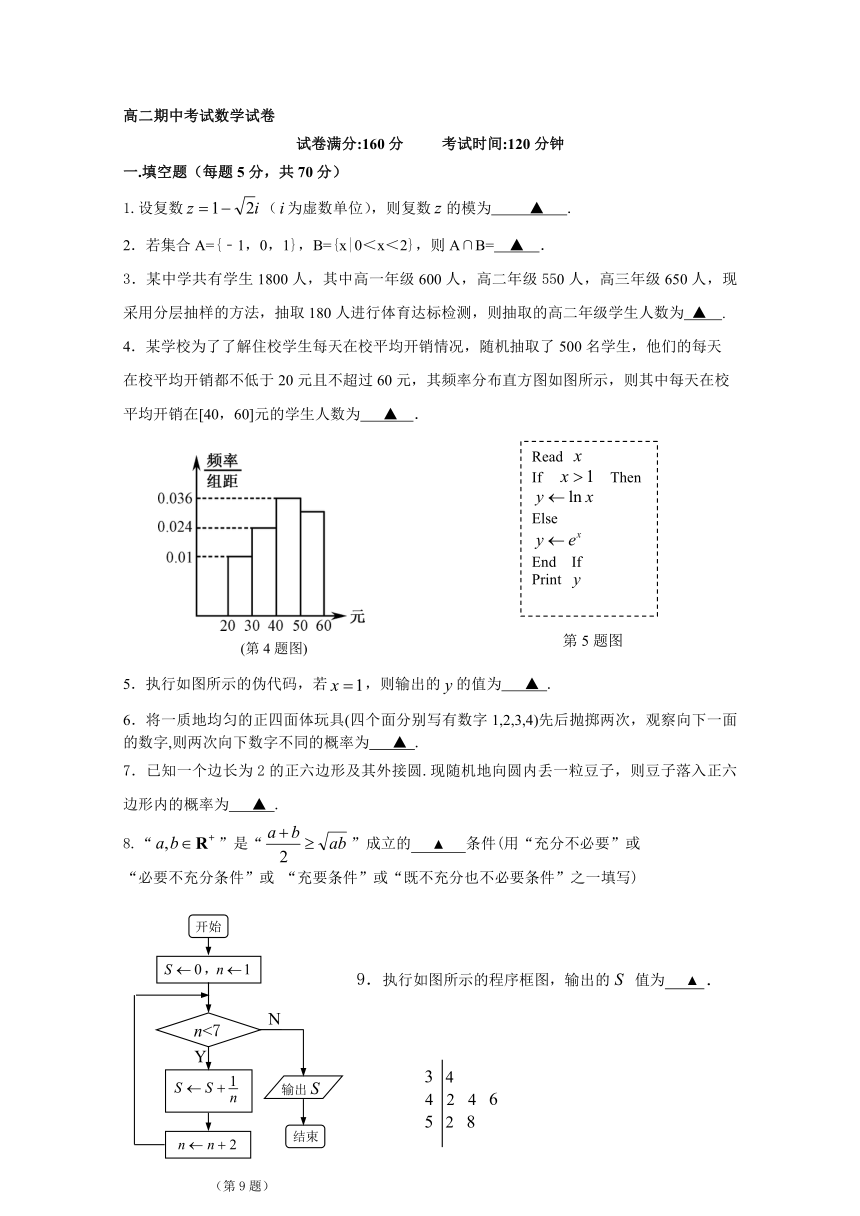 | |
| 格式 | zip | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-24 17:41:16 | ||
图片预览




文档简介
高二期中考试数学试卷
试卷满分:160分 考试时间:120分钟
一.填空题(每题5分,共70分)
1.设复数(为虚数单位),则复数的模为 ▲ .
2.若集合A={﹣1,0,1},B={x|0<x<2},则A∩B= ▲ .
3.某中学共有学生1800人,其中高一年级600人,高二年级550人,高三年级650人,现采用分层抽样的方法,抽取180人进行体育达标检测,则抽取的高二年级学生人数为 ▲ .
4.某学校为了了解住校学生每天在校平均开销情况,随机抽取了500名学生,他们的每天
在校平均开销都不低于20元且不超过60元,其频率分布直方图如图所示,则其中每天在校
平均开销在[40,60]元的学生人数为 ▲ .
5.执行如图所示的伪代码,若,则输出的的值为 ▲ .
6.将一质地均匀的正四面体玩具(四个面分别写有数字1,2,3,4)先后抛掷两次,观察向下一面的数字,则两次向下数字不同的概率为 ▲ .
7.已知一个边长为2的正六边形及其外接圆.现随机地向圆内丢一粒豆子,则豆子落入正六边形内的概率为 ▲ .
8.“”是“”成立的 ▲ 条件(用“充分不必要”或
“必要不充分条件”或 “充要条件”或“既不充分也不必要条件”之一填写)
9.执行如图所示的程序框图,输出的值为 ▲ .
10.某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则
剩下个数的方差为 ▲ .
11.设曲线在点处的切线与直线平行,则实数= ▲ .
12.已知定义在R上的函数,若 ,则实数取值范围为 ▲ .
13.已知函数,当时,的取值范围
为,则实数m的取值范围是 ▲ .
14.已知椭圆的左、右焦点为、,是椭圆上异于顶点的一点,在上,且满足,,为坐标原点.则椭圆离心率的取值范围▲.
二.解答题(共六大题,满分90分)
15.(本题满分14分)某老师从参加高二年级一次考试的学生中抽出60名学生,将其成绩(均
为整数)分成六段,,…后画出如下部分频率分布直方
图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)该老师不小心洒了一个墨点在直方图的矩形区域内,求恰好落在第二组的小矩形内的概率(不计墨点大小);
(3)若80分及以上为优秀,估计从高二年级优秀的学生中抽取一位学生分数不低于90分的概率.
16. (本题满分14分)已知,用数学归纳法证明能被8整除.
17. (本题满分14分)已知函数,
(1)当时,求关于的不等式的解集;(2) 试解关于的不等式:.
18. (本题满分16分)
已知椭圆:的右焦点为,过作直线(不过原点)交椭圆于两点,若的中点为,直线交椭圆的右准线于
(1)若直线垂直轴时,,求椭圆的离心率;
(2)若椭圆的离心率,当直线斜率存在时设为,直线的斜率设为,试求的值。
19.(本题满分16分)
南京市溧水区计划在无想山建一个竖直长度为20米的人工瀑布,同时在瀑布正前方修建一座观光电梯。如图所示,瀑布底部距离水平地面的高度为60米,电梯上设有一个安全拍照口,上升的最大高度为60米。设距离水平地面的高度为米,处拍瀑布的视角为。摄影爱好者发现,要使照片清晰,视角不能小于。
(1)当米时,视角恰好为,求电梯和山脚的水平距离。
(2)要使电梯拍照口的高度在米及以上时,拍出的照片均清晰,试求出电梯和山脚的水平距离的取值范围。
20. (本题满分16分)
已知函数,令,其中是函数的导函数.
(Ⅰ)当时,求的极值;
(Ⅱ)当时,若存在,使得:恒成立,求实数的取值范围.
参考答案高二期中数学 (理)
一:填空(70分)
1. 2. 3 . 55 4 . 330
5 . 6 . 7. 8. 充分不必要
9 . 10. 14 11. 12.
13. 14.
二:解答题
15.解:(1)因为各组的频率和等于1,故第四组的频率:
, ………………2分
直方图如右所示; ………4分
(2)记 “墨点恰好落在第二组的小矩
形内”为事件A,洒墨点是随机的,所
以认为落入每个矩形内的机会是均等的,
于是事件A的概率等于第二个矩形面积
与所有矩形的面积之比,即
故墨点恰好落在第二组的小矩形内的概率为0.15; ………………9分
(3)由图可得,80及以上的分数所在的第五、六组,频率和为,所以其中优秀的学生有人,而不低于90分所在的为第六组,频率,则不低于90分的学生有人,在优秀的学生中抽取一位学生是等可能的,有18种可能,记“优秀的18学生中抽取一位学生分数不低于90分”为事件B,则事件B包含其中的3个基本事件,所以事件B的概率为, ………………13分
利用抽样学生的成绩,故可估计从高二年级优秀的学生中抽取一位学生分数不低于90分的概率为. …………………14分
16.证明..
(1)当n=1时,,显然能被8整除;……………… 2分
(2)假设n=k(时,能被8整除,…3分
则当时,有:
因为均为奇数,它们的和必为偶数,所以能被8整除,又由假设知能被8整除,所以能被8整除,所以当时命题也成立.
综上(1)(2)可知,能被8整除. ……………14分
17.解:(1)时
,即:
令得:或 …………………2分
或 …………………5分
的解集为:……………6分
(2)
……………8分
(ⅰ)当时:
(ⅱ) 当时:
(ⅲ) 当时:
………………………………………14分
(每种情况2分)
18.解:(1),……………………………4分
由得:…………………………………………………6分
(2)得
联立得:……………8分
,…………………9分
………………………………………………………11分
直线方程为:………………………………13分
所以,即………………………………………16分
(其它解法参照给分)
19.解:(1)设,过作,垂足为。
,,…………………………………………2分
…………………………4分
解得:………………………………………………6分
解法二:用余弦定理求解给分。
(2),
……………………………8分
由题知在上恒成立…………………………………10分
在上恒成立…………………12分
解得…………………15分
答:CD的取值范围……………………………16分
解法二:利用P点轨迹方程是圆的一部分给分
20.(Ⅰ)函数定义域为:(
当时, (2分)
令解得;
当时,,当时,
所以的单调递减区间为(0,),单调递增区间为(,+∞)(4分)
所以时取得极小值,无极大值.(6分)
(Ⅱ)
当即时,恒有成立,
所以在[1,3]上是单调递减.
所以
所以,(9分)
因为存在,使得恒成立,
所以整理得
又<0,所以(12分)
令=-,则∈(2,8),构造函数,
所以,
当时,,当时,,此时函数单调递增,
当时,,此时函数单调递减,
所以,
所以m的取值范围为(,+∞). (16分)
????
试卷满分:160分 考试时间:120分钟
一.填空题(每题5分,共70分)
1.设复数(为虚数单位),则复数的模为 ▲ .
2.若集合A={﹣1,0,1},B={x|0<x<2},则A∩B= ▲ .
3.某中学共有学生1800人,其中高一年级600人,高二年级550人,高三年级650人,现采用分层抽样的方法,抽取180人进行体育达标检测,则抽取的高二年级学生人数为 ▲ .
4.某学校为了了解住校学生每天在校平均开销情况,随机抽取了500名学生,他们的每天
在校平均开销都不低于20元且不超过60元,其频率分布直方图如图所示,则其中每天在校
平均开销在[40,60]元的学生人数为 ▲ .
5.执行如图所示的伪代码,若,则输出的的值为 ▲ .
6.将一质地均匀的正四面体玩具(四个面分别写有数字1,2,3,4)先后抛掷两次,观察向下一面的数字,则两次向下数字不同的概率为 ▲ .
7.已知一个边长为2的正六边形及其外接圆.现随机地向圆内丢一粒豆子,则豆子落入正六边形内的概率为 ▲ .
8.“”是“”成立的 ▲ 条件(用“充分不必要”或
“必要不充分条件”或 “充要条件”或“既不充分也不必要条件”之一填写)
9.执行如图所示的程序框图,输出的值为 ▲ .
10.某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则
剩下个数的方差为 ▲ .
11.设曲线在点处的切线与直线平行,则实数= ▲ .
12.已知定义在R上的函数,若 ,则实数取值范围为 ▲ .
13.已知函数,当时,的取值范围
为,则实数m的取值范围是 ▲ .
14.已知椭圆的左、右焦点为、,是椭圆上异于顶点的一点,在上,且满足,,为坐标原点.则椭圆离心率的取值范围▲.
二.解答题(共六大题,满分90分)
15.(本题满分14分)某老师从参加高二年级一次考试的学生中抽出60名学生,将其成绩(均
为整数)分成六段,,…后画出如下部分频率分布直方
图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)该老师不小心洒了一个墨点在直方图的矩形区域内,求恰好落在第二组的小矩形内的概率(不计墨点大小);
(3)若80分及以上为优秀,估计从高二年级优秀的学生中抽取一位学生分数不低于90分的概率.
16. (本题满分14分)已知,用数学归纳法证明能被8整除.
17. (本题满分14分)已知函数,
(1)当时,求关于的不等式的解集;(2) 试解关于的不等式:.
18. (本题满分16分)
已知椭圆:的右焦点为,过作直线(不过原点)交椭圆于两点,若的中点为,直线交椭圆的右准线于
(1)若直线垂直轴时,,求椭圆的离心率;
(2)若椭圆的离心率,当直线斜率存在时设为,直线的斜率设为,试求的值。
19.(本题满分16分)
南京市溧水区计划在无想山建一个竖直长度为20米的人工瀑布,同时在瀑布正前方修建一座观光电梯。如图所示,瀑布底部距离水平地面的高度为60米,电梯上设有一个安全拍照口,上升的最大高度为60米。设距离水平地面的高度为米,处拍瀑布的视角为。摄影爱好者发现,要使照片清晰,视角不能小于。
(1)当米时,视角恰好为,求电梯和山脚的水平距离。
(2)要使电梯拍照口的高度在米及以上时,拍出的照片均清晰,试求出电梯和山脚的水平距离的取值范围。
20. (本题满分16分)
已知函数,令,其中是函数的导函数.
(Ⅰ)当时,求的极值;
(Ⅱ)当时,若存在,使得:恒成立,求实数的取值范围.
参考答案高二期中数学 (理)
一:填空(70分)
1. 2. 3 . 55 4 . 330
5 . 6 . 7. 8. 充分不必要
9 . 10. 14 11. 12.
13. 14.
二:解答题
15.解:(1)因为各组的频率和等于1,故第四组的频率:
, ………………2分
直方图如右所示; ………4分
(2)记 “墨点恰好落在第二组的小矩
形内”为事件A,洒墨点是随机的,所
以认为落入每个矩形内的机会是均等的,
于是事件A的概率等于第二个矩形面积
与所有矩形的面积之比,即
故墨点恰好落在第二组的小矩形内的概率为0.15; ………………9分
(3)由图可得,80及以上的分数所在的第五、六组,频率和为,所以其中优秀的学生有人,而不低于90分所在的为第六组,频率,则不低于90分的学生有人,在优秀的学生中抽取一位学生是等可能的,有18种可能,记“优秀的18学生中抽取一位学生分数不低于90分”为事件B,则事件B包含其中的3个基本事件,所以事件B的概率为, ………………13分
利用抽样学生的成绩,故可估计从高二年级优秀的学生中抽取一位学生分数不低于90分的概率为. …………………14分
16.证明..
(1)当n=1时,,显然能被8整除;……………… 2分
(2)假设n=k(时,能被8整除,…3分
则当时,有:
因为均为奇数,它们的和必为偶数,所以能被8整除,又由假设知能被8整除,所以能被8整除,所以当时命题也成立.
综上(1)(2)可知,能被8整除. ……………14分
17.解:(1)时
,即:
令得:或 …………………2分
或 …………………5分
的解集为:……………6分
(2)
……………8分
(ⅰ)当时:
(ⅱ) 当时:
(ⅲ) 当时:
………………………………………14分
(每种情况2分)
18.解:(1),……………………………4分
由得:…………………………………………………6分
(2)得
联立得:……………8分
,…………………9分
………………………………………………………11分
直线方程为:………………………………13分
所以,即………………………………………16分
(其它解法参照给分)
19.解:(1)设,过作,垂足为。
,,…………………………………………2分
…………………………4分
解得:………………………………………………6分
解法二:用余弦定理求解给分。
(2),
……………………………8分
由题知在上恒成立…………………………………10分
在上恒成立…………………12分
解得…………………15分
答:CD的取值范围……………………………16分
解法二:利用P点轨迹方程是圆的一部分给分
20.(Ⅰ)函数定义域为:(
当时, (2分)
令解得;
当时,,当时,
所以的单调递减区间为(0,),单调递增区间为(,+∞)(4分)
所以时取得极小值,无极大值.(6分)
(Ⅱ)
当即时,恒有成立,
所以在[1,3]上是单调递减.
所以
所以,(9分)
因为存在,使得恒成立,
所以整理得
又<0,所以(12分)
令=-,则∈(2,8),构造函数,
所以,
当时,,当时,,此时函数单调递增,
当时,,此时函数单调递减,
所以,
所以m的取值范围为(,+∞). (16分)
????
同课章节目录
