北师大版必修一第二章2.3.1 函数的单调性(2)(共22张)
文档属性
| 名称 | 北师大版必修一第二章2.3.1 函数的单调性(2)(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-26 00:00:00 | ||
图片预览




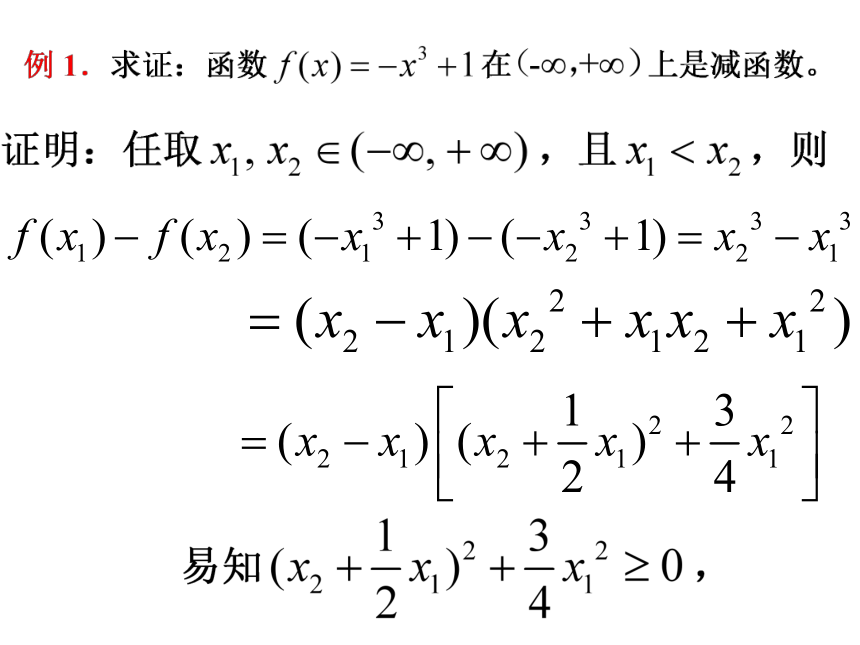
文档简介
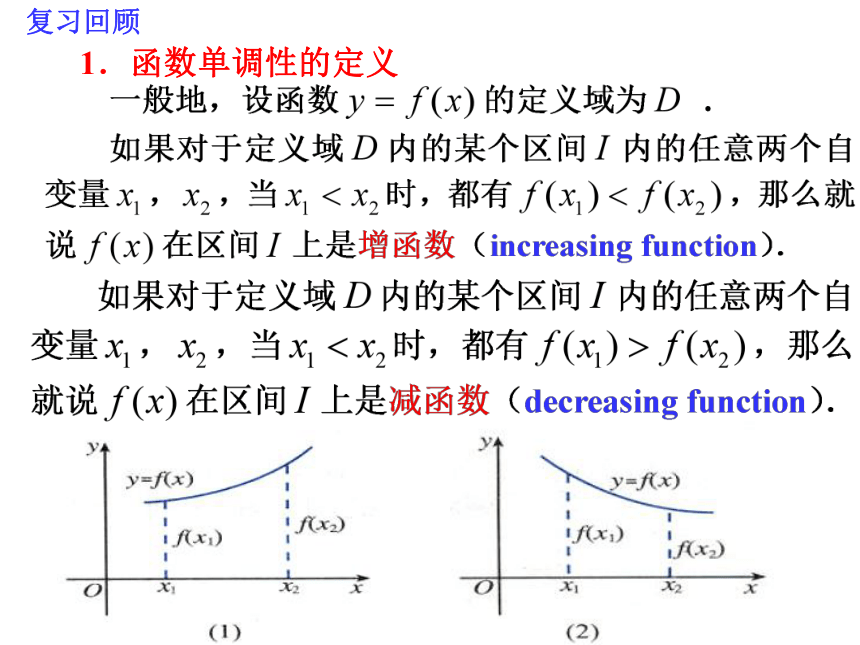
课件22张PPT。§2.3.2函数的单调性(2)复习回顾1.函数单调性的定义函数单调性定义的等价形式2.单调区间,单调性,单调函数 (1)如果y=f(x)在区间D上是增加的或是减小的,那么称D为函数y=f(x)的单调区间. (2)如果y=f(x)在定义域的某个区间I上是增加的或是减小的,那么就称函数y=f(x)在这个区间I上具有单调性. (3)如果y=f(x)在整个定义域D内是增加的或是减小的,我们分别称这个函数y=f(x)为增函数或减函数,统称为单调函数.1.任取 x1,x2∈D,且x12.作差 f(x1)-f(x2);
3.变形(通常是因式分解和配方);
4.定号(即判断差f(x1)-f(x2)的正负);
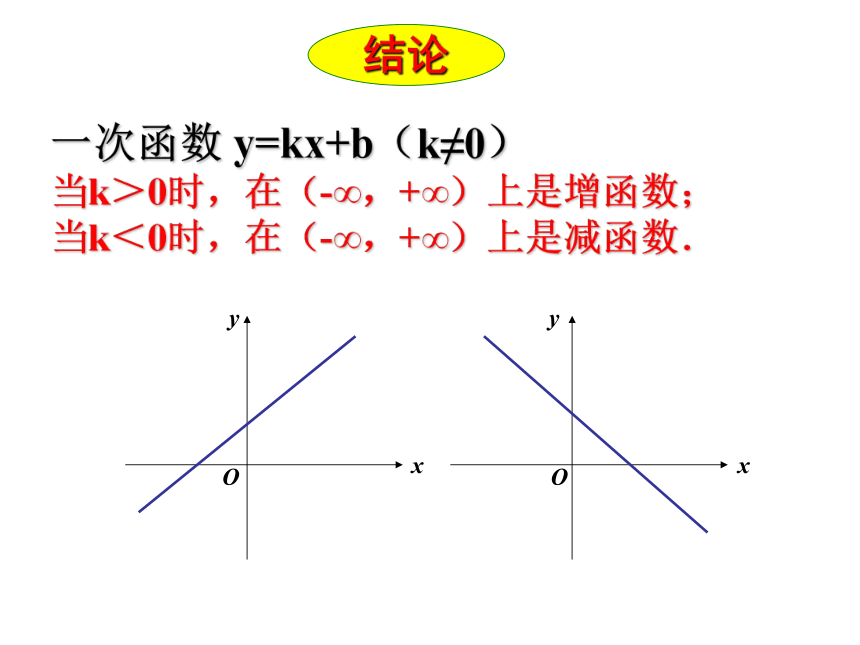
5.结论(即指出函数f(x)在给定的区间D上的单调性). 利用定义证明(判断)函数f(x)在给定的区间D上的单调性的一般步骤:一次函数 y=kx+b(k≠0)
当k>0时,在(-∞,+∞)上是增函数;
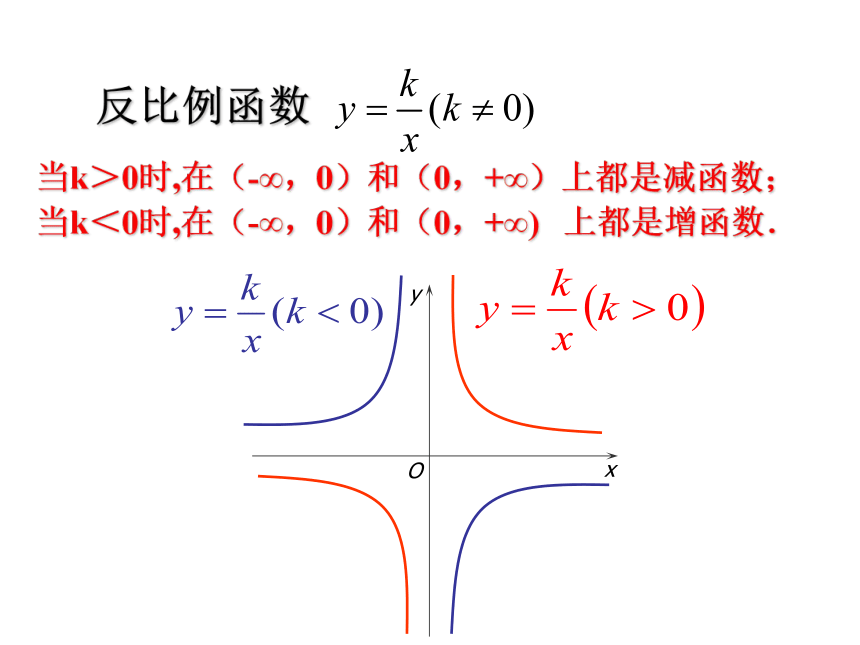
当k<0时,在(-∞,+∞)上是减函数. 结论xxyyOO当k>0时,在(-∞,0)和(0,+∞)上都是减函数;
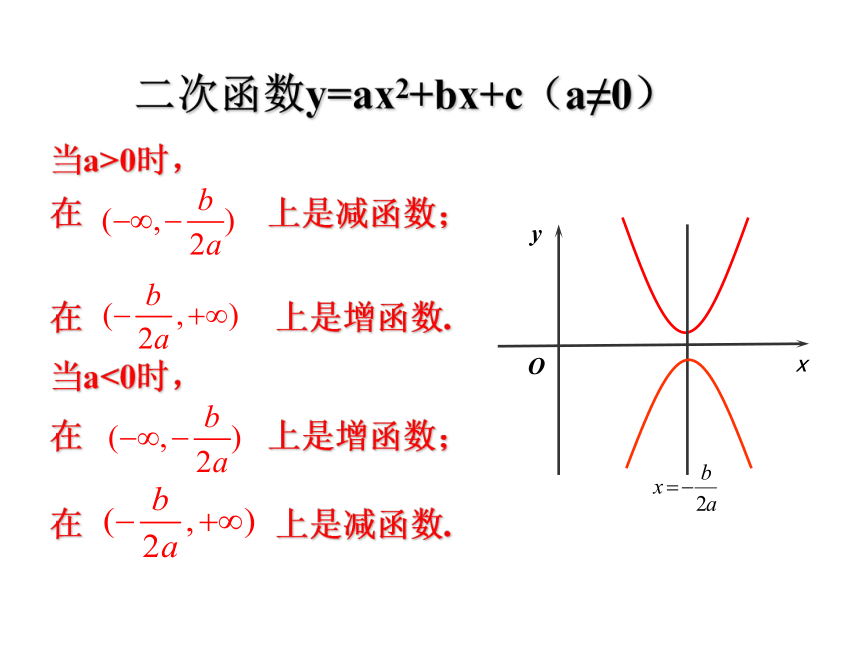
当k<0时,在(-∞,0)和(0,+∞) 上都是增函数. 二次函数y=ax2+bx+c(a≠0)
当a>0时,
在 上是减函数;
在 上是增函数.
当a<0时,
在 上是增函数;
在 上是减函数. 例5 函数f(x)对任意的m, n∈R,都有f(m+n)=f(m)+f(n)-1.并且当x > 0时,f(x)> 1.1)求证:f(x)在R上是增函数;2)已知f(3)=4,解不等式 f ( a-5) < 2.例5 函数f(x)对任意的m, n∈R,都有f(m+n)=f(m)+f(n)-1.并且当x > 0时,f(x)> 1.1)求证:f(x)在R上是增函数;2)已知f(3)=4,解不等式 f ( a-5) < 2.解: 练习DAB 4.若函数 在R上是单调增函数,
求 的取值范围。
课堂小结P40题 B组 第2题. 课外作业
3.变形(通常是因式分解和配方);
4.定号(即判断差f(x1)-f(x2)的正负);
5.结论(即指出函数f(x)在给定的区间D上的单调性). 利用定义证明(判断)函数f(x)在给定的区间D上的单调性的一般步骤:一次函数 y=kx+b(k≠0)
当k>0时,在(-∞,+∞)上是增函数;
当k<0时,在(-∞,+∞)上是减函数. 结论xxyyOO当k>0时,在(-∞,0)和(0,+∞)上都是减函数;
当k<0时,在(-∞,0)和(0,+∞) 上都是增函数. 二次函数y=ax2+bx+c(a≠0)
当a>0时,
在 上是减函数;
在 上是增函数.
当a<0时,
在 上是增函数;
在 上是减函数. 例5 函数f(x)对任意的m, n∈R,都有f(m+n)=f(m)+f(n)-1.并且当x > 0时,f(x)> 1.1)求证:f(x)在R上是增函数;2)已知f(3)=4,解不等式 f ( a-5) < 2.例5 函数f(x)对任意的m, n∈R,都有f(m+n)=f(m)+f(n)-1.并且当x > 0时,f(x)> 1.1)求证:f(x)在R上是增函数;2)已知f(3)=4,解不等式 f ( a-5) < 2.解: 练习DAB 4.若函数 在R上是单调增函数,
求 的取值范围。
课堂小结P40题 B组 第2题. 课外作业
