人教版高中数学选修1-1专题1.2充分条件与必要条件课件 (共52张)
文档属性
| 名称 | 人教版高中数学选修1-1专题1.2充分条件与必要条件课件 (共52张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-26 00:00:00 | ||
图片预览








文档简介
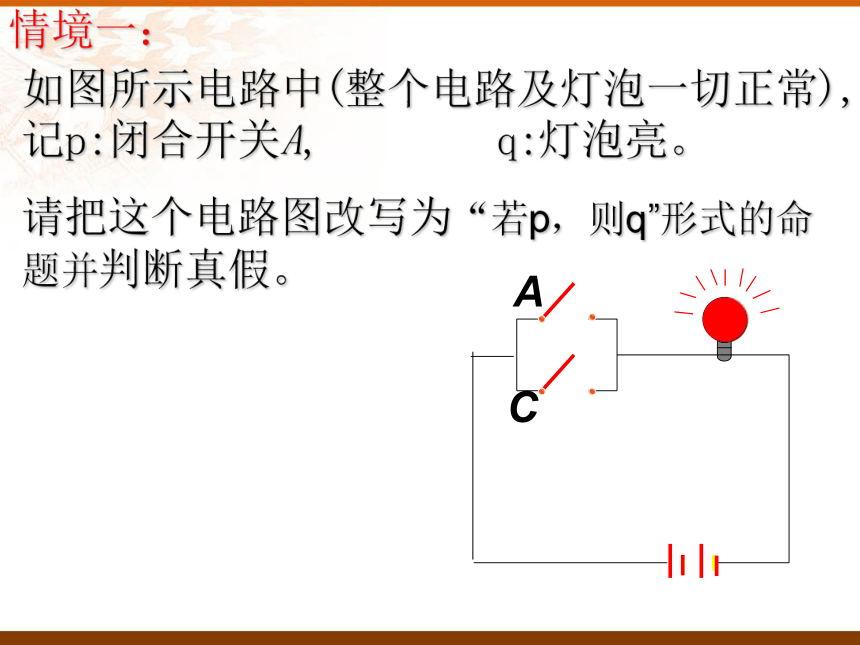
课件51张PPT。 (选修2-1)第一章 常用逻辑用语1.2.1充分条件与必要条件如图所示电路中(整个电路及灯泡一切正常),记p:闭合开关A, q:灯泡亮。
请把这个电路图改写为“若p,则q”形式的命题并判断真假。情境一:AC情境二:记p:x >2, q:x >0 。
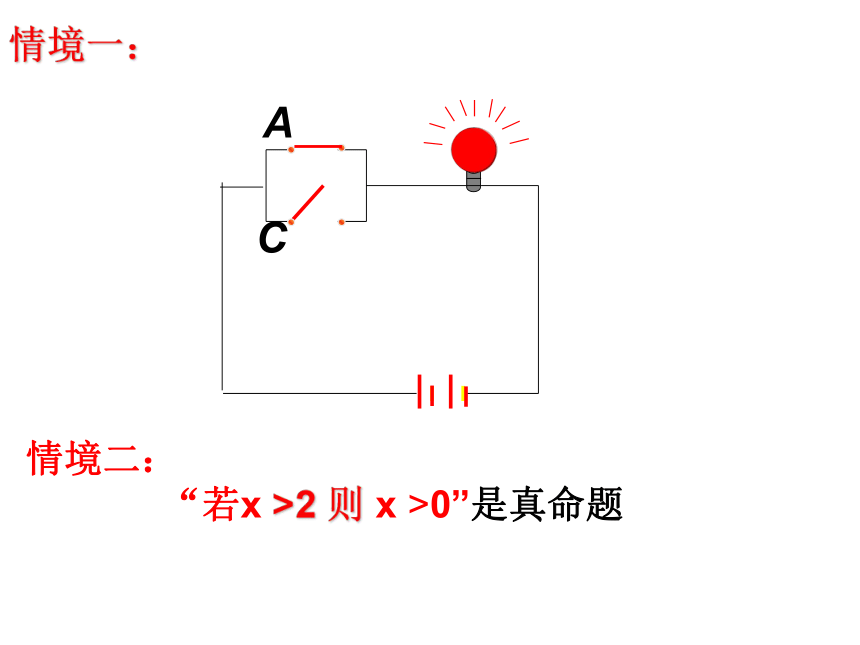
判断命题“若x >2 ,则 x >0”的真假。情境一:情境二:
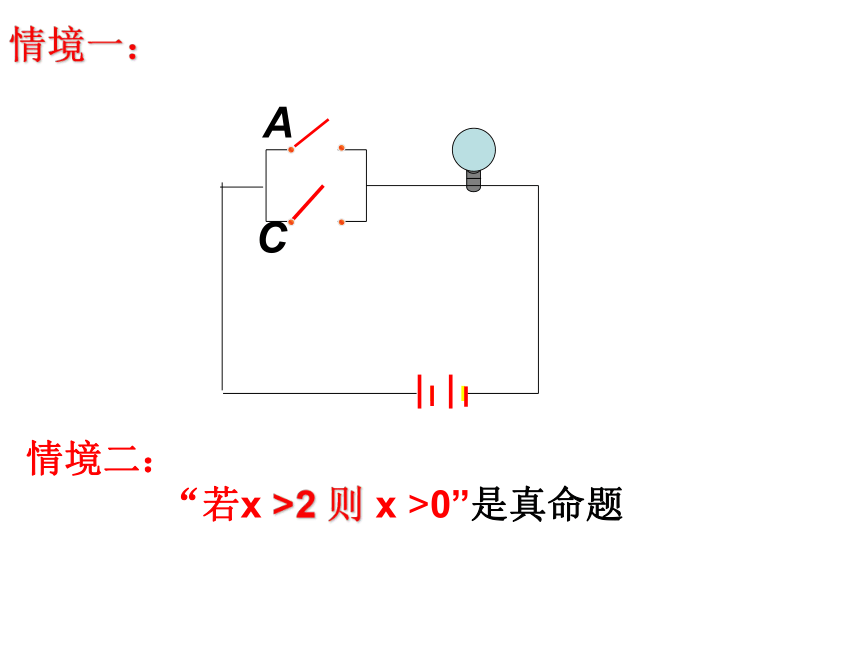
“若x >2 则 x >0”是真命题AC情境一:情境二:
“若x >2 则 x >0”是真命题ACp例1: 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?q定义应用:定义应用:p是q的充分条件吗?尝试探究1: 探究结论:①如果p是q的必要条件,那么应该有
还是①
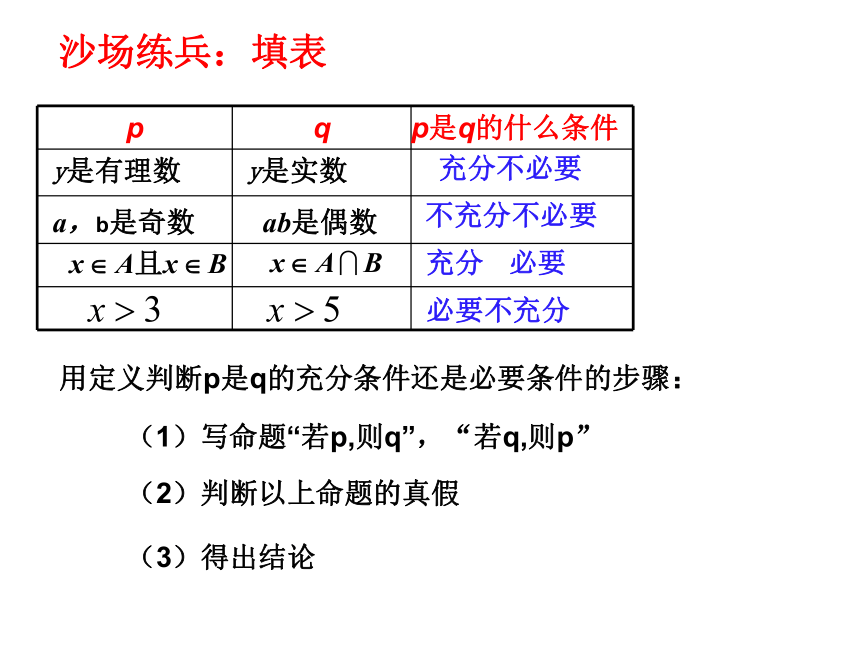
即“若q,则p”为真命题②如何判断p是q的什么条件沙场练兵:填表a,b是奇数ab是偶数不充分不必要充分不必要(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:尝试探究2:(1).试写出x>5的一个充分不必要条件 ……… (2).试写出x>5的一个必要不充分条件 ……… 深化探究:图1图2图3图4图5P={x|满足条件p}; Q={x|满足条件q}沙场练兵(福建理变式)设集合A={x| 0那么“m A”是“m B”的( )
A.充分不必要条件 B.必要不充分条件
C.充分又必要条件 D. 不充分不必要条件(2)通过本节课的学习你主要有哪些收获?(1)本节课学习后,有人问你“充分条件与必要条件”
是什么?你怎样回答他?小结:课后探讨:下列生活中名言名句的充要关系如何?
(1)骄兵必败
(2)有志者事竞成
(3)名师出高徒
(4)玉不琢,不成器 布置作业:
P12页 习题1.2A组 第三题 合作探究:
请设计四个电路图,使“开关A闭合”分别为“灯泡亮”的“充分不必要条件”、“必要不充分条件”、“既充分又必要条件”、“既不充分又不必要条件” 。练习:填表a,b是奇数ab是偶数不充分不必要必要不充分(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:尝试探究2:判断p是q的充分还是必要条件的方法: 例2: 下列“若p,则q”形式的命题中,哪些命题中的p是q的必要条件?
(1)若 是无理数,则 是无理数;
(2)若 ,则 .例 1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若 ,则 ;
(2)若 ,则 为增函数;
(3)若 为无理数,则 为无理数.pq?(1)、(2)定义应用:例例1: 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?pq?(1)、(2)定义应用:尝试探究2:从集合角度理解充分必要条件:小推大、
大不能推小2、利用集合的关系判定练习2、设集合M={x|x>2},N={x|x<3},那么“x∈M或x∈N”
是“x∈M∩N”的( )
A.充要条件 B .必要不充分条件
C .充分不必要 D .不充分不必要3、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0 A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件BBA1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要不充分条件2.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件练习 在下列各题中的p是q的什么条件?
(1) , ;
, ;
, 有实根;
是方程 的一个根, .p是q的必要不充分条件.p是q的充分不必要条件.p是q的充要条件.p是q的充要条件.练习教材12页练习探究1:若p是q的充分条件,则﹁p是﹁q的什么条件?﹁p是﹁q的必要条件. 探究2:若p是q的必要条件,则﹁p是﹁q的什么条件?﹁p是﹁q的充分条件. 新知探究探究3:若p不是q的充分条件,则q可能是p的必要条件吗?p可能是q的必要条件吗?新知探究如果p不是q的充分条件,则q也不是p
的必要条件.充分条件与必要条件是共存的p是q的充分不必要条件。p是q的充要条件。p是q的必要不充分条件。p是q的既不充分也不必要条件。P q p是q的充分条件--------有它就行
q p p是q的必要条件--------缺它不行小结:练习 2 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若两个三角形全等,则这两个三角形相似;
(2)若 ,则 .是真命题,所以命题中的p是q的充分条件.是假命题,所以命题中的p不是q的充分条件.教材10页练习pq?充分充分必要充分必要必要A充分若p q,又有q p,且称p与q互为充要条件.若 ,且 ,则p是q的必要不充分条件; 1、直接用定义判断归纳:判断充分条件、必要条件的方法“若p,则q”原命题为真逆命题为假; 原命题为假逆命题为真; 原命题、逆命题都为真; 原命题、逆命题都为假. 上述四种关系实质归结为原命题和逆命题的真假性
例与练:填表充分不必要必要不充分充分不必要必要不充分(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:例与练:填表充分不必要必要不充分充分不必要必要不充分(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:⒈ 判断下列“若p则q”形式命题的真假,并研究其逆命题的真假.(1)若x >2 则 x >0;真逆:若x >0 则 x >2;假假真推断符号“ ”的含义 如果命题“若p则q”为真,则记作p q
(或q p)。如果命题“若p则q”为假,则记作p q
(或q p)。练习 1 用符号“ ”与“ ”填空:
(1) ;
(2)内错角相等 两直线平行;
(3)整数 能被6相除 的个位数字为偶数;
(4) .教材10页练习a = 0 ab=0。
要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab=0是a =0的必要条件。
则a = 0 是 ab=0的充分条件
则ab=0 是 a = 0的必要条件
定义1 “若p,则q”为真命题,是指由p可以推出q,记作p q,并且说p是q的充分条件,q是p的必要条件.定义2 “若p,则q”为假命题,是指由p不可以推出q,记作p q,并且说p不是q的充分条件,q不是p的必要条件.例如:(1)若 ,则 .
(2)若 ,则 .命题(1)为真命题,命题(2)为假命题.所以 是 的充分条件;
是 的必要条件. 所以 不是 的充分条件;
不是 的必要条件. 例 1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若 ,则 ;
(2)若 ,则 为增函数;
(3)若 为无理数,则 为无理数.pq?(1)、(2)哪些命题中的q是p的必要条件?变式 3 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1)若 是无理数,则 是无理数;
是真命题,所以命题中的q是p的必要条件.pq?p与q互为充要条件.例 下列各题中,哪些p是q的充要条件?
(1) , ;
(2) , , ;
(3) , .解:在(1) (3) 中,p q,所以 (1)(3)中的p是q的充要条件.在(2)中,q p,所以(2)中的p不是q的充要条件. 教材11页例3定义 3 既有p q,又有q p,就记作p q,且称p与q互为充要条件.若 ,且 ,则p是q的必要不充分条件; q是p的既不充分也不必要条件.例.填表典型例题充分不必要必要不充分充分不必要必要不充分必要不充分充分不必要(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:尝试探究2:从集合角度理解充分必要条件:小推大、
大不能推小尝试探究2:小推大、
大不能推小深化探究: 图1图2图3图4图5P={x|满足条件p}; Q={x|满足条件q} PQP、QPQPQ练习:填表不充分不必要 充分且必要(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:必要不充分请你做一做 1.找一找我们所学过的定理中的p是q的什么条件2.生活中可以体现充分条件与必要条件的实例
请把这个电路图改写为“若p,则q”形式的命题并判断真假。情境一:AC情境二:记p:x >2, q:x >0 。
判断命题“若x >2 ,则 x >0”的真假。情境一:情境二:
“若x >2 则 x >0”是真命题AC情境一:情境二:
“若x >2 则 x >0”是真命题ACp例1: 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?q定义应用:定义应用:p是q的充分条件吗?尝试探究1: 探究结论:①如果p是q的必要条件,那么应该有
还是①
即“若q,则p”为真命题②如何判断p是q的什么条件沙场练兵:填表a,b是奇数ab是偶数不充分不必要充分不必要(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:尝试探究2:(1).试写出x>5的一个充分不必要条件 ……… (2).试写出x>5的一个必要不充分条件 ……… 深化探究:图1图2图3图4图5P={x|满足条件p}; Q={x|满足条件q}沙场练兵(福建理变式)设集合A={x| 0
A.充分不必要条件 B.必要不充分条件
C.充分又必要条件 D. 不充分不必要条件(2)通过本节课的学习你主要有哪些收获?(1)本节课学习后,有人问你“充分条件与必要条件”
是什么?你怎样回答他?小结:课后探讨:下列生活中名言名句的充要关系如何?
(1)骄兵必败
(2)有志者事竞成
(3)名师出高徒
(4)玉不琢,不成器 布置作业:
P12页 习题1.2A组 第三题 合作探究:
请设计四个电路图,使“开关A闭合”分别为“灯泡亮”的“充分不必要条件”、“必要不充分条件”、“既充分又必要条件”、“既不充分又不必要条件” 。练习:填表a,b是奇数ab是偶数不充分不必要必要不充分(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:尝试探究2:判断p是q的充分还是必要条件的方法: 例2: 下列“若p,则q”形式的命题中,哪些命题中的p是q的必要条件?
(1)若 是无理数,则 是无理数;
(2)若 ,则 .例 1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若 ,则 ;
(2)若 ,则 为增函数;
(3)若 为无理数,则 为无理数.pq?(1)、(2)定义应用:例例1: 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?pq?(1)、(2)定义应用:尝试探究2:从集合角度理解充分必要条件:小推大、
大不能推小2、利用集合的关系判定练习2、设集合M={x|x>2},N={x|x<3},那么“x∈M或x∈N”
是“x∈M∩N”的( )
A.充要条件 B .必要不充分条件
C .充分不必要 D .不充分不必要3、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0
C.充要条件 D.既非充分又非必要条件BBA1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要不充分条件2.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件练习 在下列各题中的p是q的什么条件?
(1) , ;
, ;
, 有实根;
是方程 的一个根, .p是q的必要不充分条件.p是q的充分不必要条件.p是q的充要条件.p是q的充要条件.练习教材12页练习探究1:若p是q的充分条件,则﹁p是﹁q的什么条件?﹁p是﹁q的必要条件. 探究2:若p是q的必要条件,则﹁p是﹁q的什么条件?﹁p是﹁q的充分条件. 新知探究探究3:若p不是q的充分条件,则q可能是p的必要条件吗?p可能是q的必要条件吗?新知探究如果p不是q的充分条件,则q也不是p
的必要条件.充分条件与必要条件是共存的p是q的充分不必要条件。p是q的充要条件。p是q的必要不充分条件。p是q的既不充分也不必要条件。P q p是q的充分条件--------有它就行
q p p是q的必要条件--------缺它不行小结:练习 2 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若两个三角形全等,则这两个三角形相似;
(2)若 ,则 .是真命题,所以命题中的p是q的充分条件.是假命题,所以命题中的p不是q的充分条件.教材10页练习pq?充分充分必要充分必要必要A充分若p q,又有q p,且称p与q互为充要条件.若 ,且 ,则p是q的必要不充分条件; 1、直接用定义判断归纳:判断充分条件、必要条件的方法“若p,则q”原命题为真逆命题为假; 原命题为假逆命题为真; 原命题、逆命题都为真; 原命题、逆命题都为假. 上述四种关系实质归结为原命题和逆命题的真假性
例与练:填表充分不必要必要不充分充分不必要必要不充分(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:例与练:填表充分不必要必要不充分充分不必要必要不充分(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:⒈ 判断下列“若p则q”形式命题的真假,并研究其逆命题的真假.(1)若x >2 则 x >0;真逆:若x >0 则 x >2;假假真推断符号“ ”的含义 如果命题“若p则q”为真,则记作p q
(或q p)。如果命题“若p则q”为假,则记作p q
(或q p)。练习 1 用符号“ ”与“ ”填空:
(1) ;
(2)内错角相等 两直线平行;
(3)整数 能被6相除 的个位数字为偶数;
(4) .教材10页练习a = 0 ab=0。
要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab=0是a =0的必要条件。
则a = 0 是 ab=0的充分条件
则ab=0 是 a = 0的必要条件
定义1 “若p,则q”为真命题,是指由p可以推出q,记作p q,并且说p是q的充分条件,q是p的必要条件.定义2 “若p,则q”为假命题,是指由p不可以推出q,记作p q,并且说p不是q的充分条件,q不是p的必要条件.例如:(1)若 ,则 .
(2)若 ,则 .命题(1)为真命题,命题(2)为假命题.所以 是 的充分条件;
是 的必要条件. 所以 不是 的充分条件;
不是 的必要条件. 例 1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若 ,则 ;
(2)若 ,则 为增函数;
(3)若 为无理数,则 为无理数.pq?(1)、(2)哪些命题中的q是p的必要条件?变式 3 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1)若 是无理数,则 是无理数;
是真命题,所以命题中的q是p的必要条件.pq?p与q互为充要条件.例 下列各题中,哪些p是q的充要条件?
(1) , ;
(2) , , ;
(3) , .解:在(1) (3) 中,p q,所以 (1)(3)中的p是q的充要条件.在(2)中,q p,所以(2)中的p不是q的充要条件. 教材11页例3定义 3 既有p q,又有q p,就记作p q,且称p与q互为充要条件.若 ,且 ,则p是q的必要不充分条件; q是p的既不充分也不必要条件.例.填表典型例题充分不必要必要不充分充分不必要必要不充分必要不充分充分不必要(1)确定条件是什么?结论是什么?(2)然后尝试从条件推结论,结论推条件(3)确定条件是结论的什么条件?充分条件与必要条件定义判断的步骤:尝试探究2:从集合角度理解充分必要条件:小推大、
大不能推小尝试探究2:小推大、
大不能推小深化探究: 图1图2图3图4图5P={x|满足条件p}; Q={x|满足条件q} PQP、QPQPQ练习:填表不充分不必要 充分且必要(1)写命题“若p,则q”,“若q,则p”(2)判断以上命题的真假(3)得出结论用定义判断p是q的充分条件还是必要条件的步骤:必要不充分请你做一做 1.找一找我们所学过的定理中的p是q的什么条件2.生活中可以体现充分条件与必要条件的实例
