苏教版必修1 2.2.2 函数的奇偶性课件 (共20张PPT)
文档属性
| 名称 | 苏教版必修1 2.2.2 函数的奇偶性课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-26 08:39:31 | ||
图片预览







文档简介
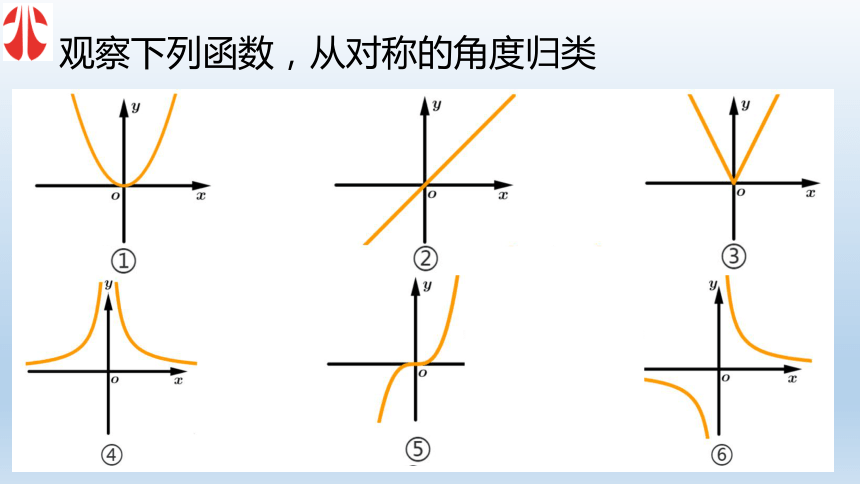
课件20张PPT。函数的奇偶性观赏生活中的对称美观赏生活中的对称美观赏生活中的对称美观赏生活中的对称美观察下列函数,从对称的角度归类xyo 一、观察二次函数 并思考以下问题:
(1)结合函数的解析式,从“数”上观察特征?
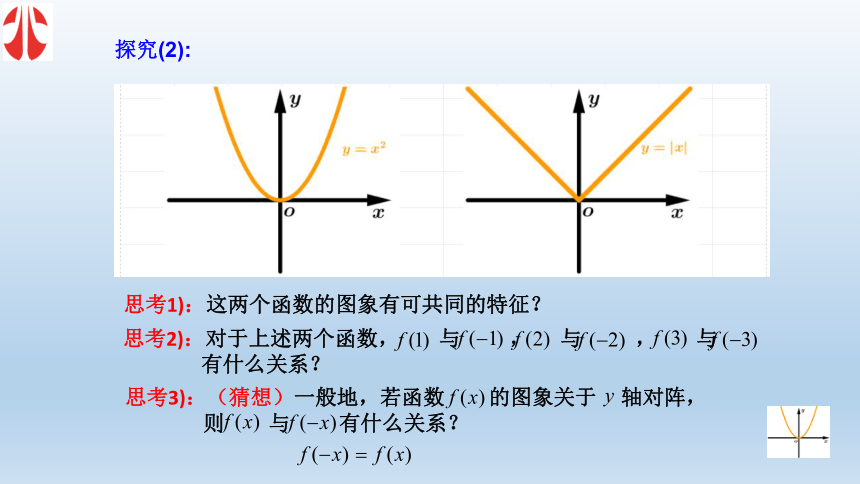
(2)结合函数的图象,从“形”上观察特征?从这个表格中大家发现有什么规律?发现:当自变量相反时函数值相等.探究(1)探究(2):
思考1):这两个函数的图象有可共同的特征?思考2):对于上述两个函数, 与 , 与 , 与
有什么关系? 思考3):(猜想)一般地,若函数 的图象关于 轴对阵,
则 与 有什么关系?探究(2):
思考4):等式 用文字语言怎样表述? 思考5):我们把具有上述特征的函数叫做偶函数,那么怎么定义偶函数呢?当自变量相反时对应的函数值相等.
如果对于函数定义域内的任意一个 ,都有 .那么 就叫偶函数.
偶函数定义:
如果对于函数定义域内的任意一个 ,都有 . 那么 就叫偶函数.
奇函数定义: 如果对于函数定义域内的任意一个 ,都有 .那么 就叫奇函数. 二、观察反比例函数 并思考以下问题:
(1)结合函数的解析式,从“数”上观察特征?
(2)结合函数的图象,从“形”上观察特征?对定义的进一步理解
等式 是偶函数吗? 偶函数的定义域有什么特征? 偶函数的定义域关于原点对称奇偶函数定义进一步理解:● 如果一个函数 是奇函数或者是偶函数, 在其定义域
内,则相反数 也必在其定义域内. 即:定义域关于原
点对称是函数具有奇偶性的前提条件.
● 如果定义域不关于原点对称,则直接得出非奇非偶函数. 练习1:判断下列区间是否关于原点对称(1) R
(2) (-1,1)
(3)(-1,1]
(4)
(5)
(6)
例1. 从定义出发,判断下列函数的奇偶性?解:定义域:
是奇函数.解:定义域:
是偶函数.练习2:从定义出发,判断下列函数的奇偶性?解:定义域:
解:分类讨论:
当 时, 为偶函数
当 时, 为非奇非偶函数.练习3:判断函数的奇偶性?趣味游戏:老师必胜!游戏规则:在圆形的桌面上摆面值相同的硬币,硬币不能重叠.老师先放,同学后放.谁在圆形桌面上摆不下硬币,谁就算输。老师一定有办法让同学输掉比赛,这是为什么吗?以同桌为单位进行游戏,然后说出理由!
小结:偶函数定义:
奇函数定义:
函数奇偶性的判断方法:
本节课用到的数学思想有哪些呢?
如果对于函数定义域内的任意一个 ,都有 . 那么 就叫偶函数. 如果对于函数定义域内的任意一个 ,都有 . 那么 就叫奇函数. 作业: 学案:1.自主测试
2.高考链接
3.选做题 谢谢大家,再见!
(1)结合函数的解析式,从“数”上观察特征?
(2)结合函数的图象,从“形”上观察特征?从这个表格中大家发现有什么规律?发现:当自变量相反时函数值相等.探究(1)探究(2):
思考1):这两个函数的图象有可共同的特征?思考2):对于上述两个函数, 与 , 与 , 与
有什么关系? 思考3):(猜想)一般地,若函数 的图象关于 轴对阵,
则 与 有什么关系?探究(2):
思考4):等式 用文字语言怎样表述? 思考5):我们把具有上述特征的函数叫做偶函数,那么怎么定义偶函数呢?当自变量相反时对应的函数值相等.
如果对于函数定义域内的任意一个 ,都有 .那么 就叫偶函数.
偶函数定义:
如果对于函数定义域内的任意一个 ,都有 . 那么 就叫偶函数.
奇函数定义: 如果对于函数定义域内的任意一个 ,都有 .那么 就叫奇函数. 二、观察反比例函数 并思考以下问题:
(1)结合函数的解析式,从“数”上观察特征?
(2)结合函数的图象,从“形”上观察特征?对定义的进一步理解
等式 是偶函数吗? 偶函数的定义域有什么特征? 偶函数的定义域关于原点对称奇偶函数定义进一步理解:● 如果一个函数 是奇函数或者是偶函数, 在其定义域
内,则相反数 也必在其定义域内. 即:定义域关于原
点对称是函数具有奇偶性的前提条件.
● 如果定义域不关于原点对称,则直接得出非奇非偶函数. 练习1:判断下列区间是否关于原点对称(1) R
(2) (-1,1)
(3)(-1,1]
(4)
(5)
(6)
例1. 从定义出发,判断下列函数的奇偶性?解:定义域:
是奇函数.解:定义域:
是偶函数.练习2:从定义出发,判断下列函数的奇偶性?解:定义域:
解:分类讨论:
当 时, 为偶函数
当 时, 为非奇非偶函数.练习3:判断函数的奇偶性?趣味游戏:老师必胜!游戏规则:在圆形的桌面上摆面值相同的硬币,硬币不能重叠.老师先放,同学后放.谁在圆形桌面上摆不下硬币,谁就算输。老师一定有办法让同学输掉比赛,这是为什么吗?以同桌为单位进行游戏,然后说出理由!
小结:偶函数定义:
奇函数定义:
函数奇偶性的判断方法:
本节课用到的数学思想有哪些呢?
如果对于函数定义域内的任意一个 ,都有 . 那么 就叫偶函数. 如果对于函数定义域内的任意一个 ,都有 . 那么 就叫奇函数. 作业: 学案:1.自主测试
2.高考链接
3.选做题 谢谢大家,再见!
