2018-2019学年第二学期上海市虹口区期中学生学习能力诊断测试初三数学试卷(含答案)
文档属性
| 名称 | 2018-2019学年第二学期上海市虹口区期中学生学习能力诊断测试初三数学试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-26 07:12:27 | ||
图片预览


文档简介
虹口区2018学年度第二学期期中学生学习能力诊断测试
初三数学 试卷
(满分150分,考试时间100分钟) 2019.04
考生注意:
1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.的计算结果为
A.; B.; C.; D..
2.方程 的解为
A.; B.; C.; D..
3.已知一次函数,如果y随自变量x的增大而增大,那么a的取值范围为
A.; B.; C.; D..
4.下列事件中,必然事件是
A.在体育中考中,小明考了满分; B.经过有交通信号灯的路口,遇到红灯;
C.抛掷两枚正方体骰子,点数和大于1; D.四边形的外角和为180度.
5.正六边形的半径与边心距之比为
A.; B.; C.; D..
6.如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,
如果点B在⊙D内,点C在⊙D外,那么r可以取
A.2; B.3;
C.4; D.5.
二、填空题:(本大题共12题,每题4分,满分48分)
[请将结果直接填入答题纸的相应位置]
7.计算:= ▲ .
8. 在数轴上,表示实数的点在原点的 ▲ 侧(填“左”或“右”).
9.不等式 的正整数解为 ▲ .
10.如果关于的方程有两个相等的实数根,那么的值为 ▲ .
11.如果反比例函数的图像经过(1,3),那么该反比例函数的解析式为 ▲ .
12.如果将抛物线向左平移3个单位,那么所得新抛物线的表达式为 ▲ .
13. 一个不透明的袋中装有4个白球和若干个红球,这些球除颜色外其他都相同,摇匀后随机摸出一个球,如果摸到白球的概率为0.4,那么红球有 ▲ 个.
14. 为了了解初三毕业班学生一分钟跳绳次数的情况,某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试,将所得数据进行处理,共分成4组,频率分布表(不完整)如下表所示.如果次数在110次(含110次)以上为达标,那么估计该校初三毕业生一分钟跳绳次数的达标率约为 ▲ .
15.已知两圆外切,圆心距为7,其中一个圆的半径为3,那么另一个圆的半径长为 ▲ .
16.如图,AD∥BC,BC=2AD,AC与BD相交于点O,如果,,那么用、
表示向量是 ▲ .
17.我们知道,四边形不具有稳定性,容易变形.一个矩形发生变形后成为一个平行四边形,
设这个平行四边形相邻两个内角中较小的一个内角为,我们把的值叫做这个平行四边形的变形度.如图,矩形ABCD 的面积为5,如果变形后的平行四边形A1B1C1D1的面积为3,那么这个平行四边形的变形度为 ▲ .
18.如图,在矩形ABCD中,AB=6,点E在边AD上且AE=4,点F是边BC上的一个动点,将四边形ABFE沿EF翻折,A、B的对应点A1、B1与点C在同一直线上,A1B1与边AD交于点G,如果DG=3,那么BF的长为 ▲ .
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
先化简,再求值:,其中.
20.(本题满分10分)
解方程组:
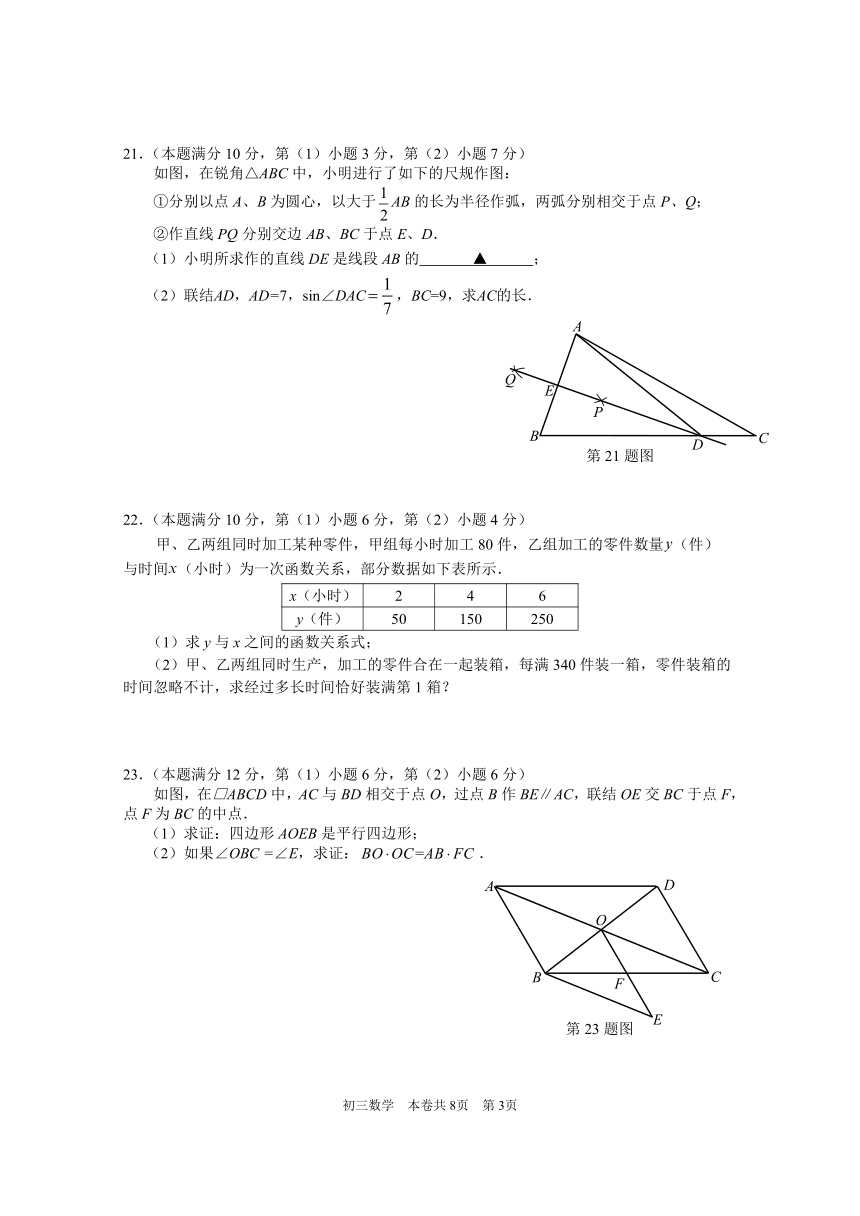
21.(本题满分10分,第(1)小题3分,第(2)小题7分)
如图,在锐角△ABC中,小明进行了如下的尺规作图:
①分别以点A、B为圆心,以大于AB的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D.
(1)小明所求作的直线DE是线段AB的 ▲ ;
(2)联结AD,AD=7,sin∠DAC,BC=9,求AC的长.
22.(本题满分10分,第(1)小题6分,第(2)小题4分)
甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量(件)
与时间(小时)为一次函数关系,部分数据如下表所示.
x(小时) 2 4 6
y(件) 50 150 250
(1)求y与x之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的
时间忽略不计,求经过多长时间恰好装满第1箱?
23.(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,在□ABCD中,AC与BD相交于点O,过点B作BE∥AC,联结OE交BC于点F,点F为BC的中点.
(1)求证:四边形AOEB是平行四边形;
(2)如果∠OBC =∠E,求证:.
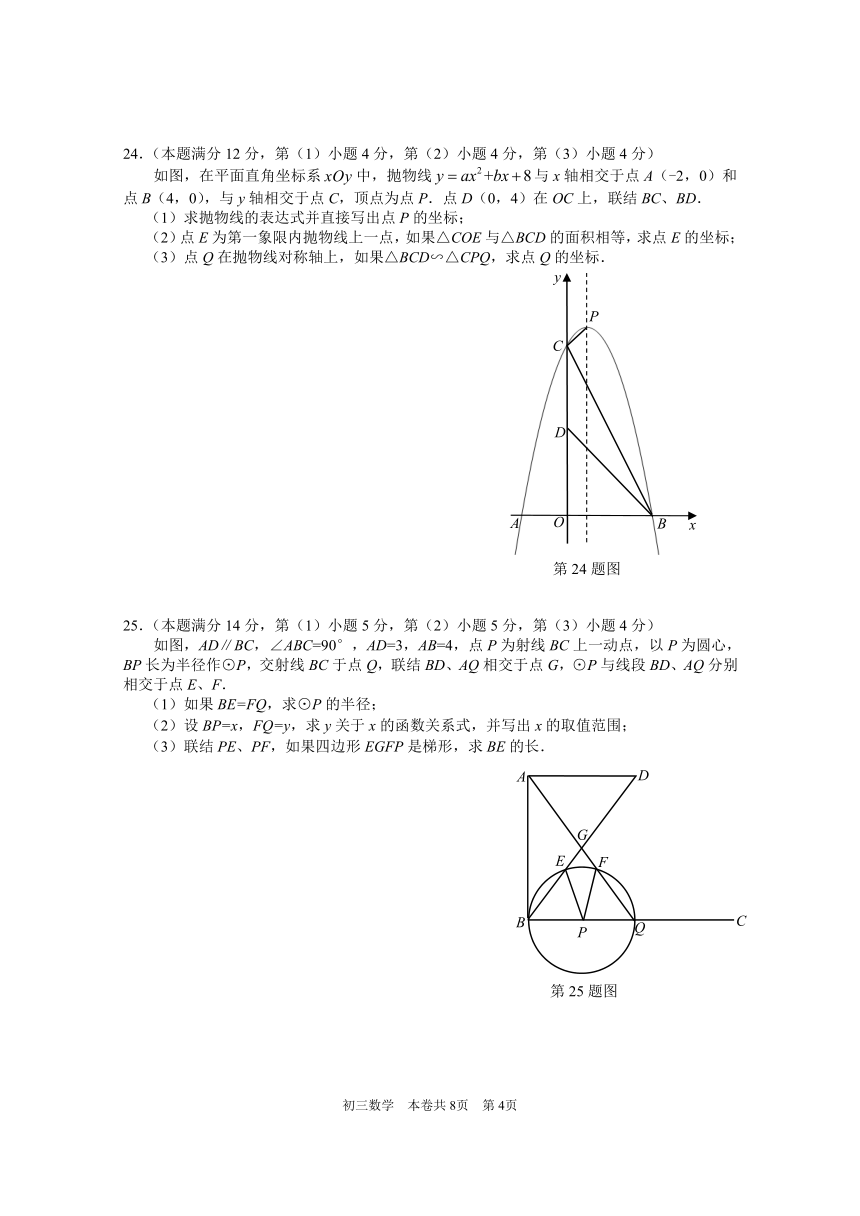
24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)
如图,在平面直角坐标系中,抛物线与x轴相交于点A(-2,0)和点B(4,0),与y轴相交于点C,顶点为点P.点D(0,4)在OC上,联结BC、BD.
(1)求抛物线的表达式并直接写出点P的坐标;
(2)点E为第一象限内抛物线上一点,如果△COE与△BCD的面积相等,求点E的坐标;
(3)点Q在抛物线对称轴上,如果△BCD∽△CPQ,求点Q的坐标.
25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)
如图,AD∥BC,∠ABC=90°,AD=3,AB=4,点P为射线BC上一动点,以P为圆心,BP长为半径作⊙P,交射线BC于点Q,联结BD、AQ相交于点G,⊙P与线段BD、AQ分别相交于点E、F.
(1)如果BE=FQ,求⊙P的半径;
(2)设BP=x,FQ=y,求y关于x的函数关系式,并写出x的取值范围;
(3)联结PE、PF,如果四边形EGFP是梯形,求BE的长.
虹口区2018学年度第二学期期中学生学习能力诊断测试
初三数学评分参考建议
2019.4
说明:
1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特别说明,每题评分只有满分或零分;
3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以1分为基本单位.
一、选择题(本大题共6题,每题4分,满分24分)
1.B 2.D 3.A 4.C 5.D 6.B
二、填空题本大题共12题,每题4分,满分48分)
7. 8.左 9.x=1 10.1
11. 12. 13.6 14.92%
15.4 16. 17. 18.
三、解答题(本大题共7题,满分78分)
19.解:原式=
当时, 原式=
20.解:由①得, 或
将它们与方程②分别组成方程组,得:
分别解这两个方程组,
得原方程组的解为 .
(代入消元法参照给分)
21.解:(1)垂直平分线(或中垂线)
(2)过点D作DF⊥AC,垂足为点F
∵DE是线段AB的垂直平分线 ∴AD=BD=7
∴
在Rt△ADF中,
在Rt△ADF中,
同理,
∴
22.解:(1)设y与x之间的函数关系式为
把(2,50)(4,150)代入
得解得
∴y与x之间的函数关系式为.
(2)设经过x小时恰好装满第1箱
根据题意得
∴
答:经过3小时恰好装满第1箱.
23.(1)证明:∵BE∥AC ∴
∵点F为BC的中点 ∴CF=BF ∴OC=BE
∵四边形ABCD是平行四边形 ∴AO=CO
∴AO=BE
∵BE∥AC ∴四边形AOEB是平行四边形
(2)证明:∵四边形AOEB是平行四边形 ∴∠BAO =∠E
∵∠OBC =∠E ∴∠BAO =∠OBC
∵∠ACB =∠BCO ∴△COB∽△CBA
∴
∵四边形ABCD是平行四边形 ∴AC=2OC
∵点F为BC的中点 ∴BC=2FC
∴
即
24.解:(1)把点A(-2,0)和点B(4,0)代入
得 解得
∴
∴P(1,9)
(2)可得点C(0,8)
设E()(x>0)
根据题意
∴
解得
E(2,8)
(3)设点M为抛物线对称轴上点P下方一点
可得tan∠CPM=tan∠ODB=1
∴∠CPM=∠ODB=45°
∴点Q在抛物线对称轴上且在点P的上方
∴∠CPQ=∠CDB=135°
∵△BCD∽△CPQ
①
∴ 解得
∴点Q(1,11)
②
∴ 解得
∴点Q(1,10)
综上所述,点Q(1,11)或(1,10)
25.(1)∵BE=FQ ∴∠BPE=∠FPQ
∵PE=PB ∴∠EBP=(180°-∠EPB)
同理∠FQP =(180°-∠FPQ) ∴∠EBP=∠FQP
∵AD∥BC ∴∠ADB=∠EBP ∴∠FQP =∠ADB
∴tan∠FQP =tan∠ADB=
设⊙P的半径为r
∴ 解得r=
∴⊙P的半径为
(2)过点P作PM⊥FQ,垂足为点M
在Rt△ABQ中,
在Rt△PQM中,
∵PM⊥FQ ∴FQ=2QM
∴()
(3)设BP=x
①EP∥AQ
∴∠EPB=∠AQB ∴tan∠EPB=tan∠AQB
可求得tan∠EPB=
∴ 解得
∴
②PF∥BD
∴∠DBC=∠FPQ ∴tan∠DBC=tan∠FPQ
过点F作FN⊥PQ,垂足为点N
可得 ,
∴
∴ 解得x=1
∴
综上所述或
A
C
D
第6题图
B
A
C
D
第16题图
B
OD
组别 分组(含最小值,不含最大值) 频数 频率
1 90~100 3 0.06
2 100~110 1 a
3 110~120 24 0.48
4 120~130 b c
第14题表
第14题表
C
第18题图
A
B
D
E
第17题图
A
B
C
D
D1
A1
B1
C1
①
②
C
第21题图
D
B
A
E
P
Q
O
E
第23题图
C
A
B
D
F
第24题图
x
B
O
C
D
A
y
P
E
第25题图
C
A
B
D
Q
F
P
G
PAGE
初三数学 本卷共4页 第3页
同课章节目录
