【备考2019中考数学学案】第六单元 圆 第3节 圆的有关计算
文档属性
| 名称 | 【备考2019中考数学学案】第六单元 圆 第3节 圆的有关计算 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-28 00:00:00 | ||
图片预览




文档简介
第六单元 圆
第3节 圆的有关计算
考 点 知 识 清 单
考点一 正多边形和圆
性质
n个顶点把圆n等分,顺次连接各分点可作出圆的内接正多边形
正多
边形
外心
正多边形①_________________________。
半径
正多边形②_________________________。
中心角
正多边形各边对的③________________________。
边心距
中心到正多边形的一边的距离。
【温馨提示】
1.正n边形的对称性:正n边形是轴对称图形,有n条对称轴,当n是偶数时,它也是中心对称图形,对称中心为正n边形的中心,
2.正n边形的有关计算:
(1)正n边形的内角=;n正n边形的外角=;正n边形的中心角。
(2)正n边形的半径R,边长a,边心距r的数量关系是:。
(3)正n边形的周长,面积S=.
(4)正六边形的边长等于半径,正三角形的边长等于其半径的倍,正方形的边长等于其半径的倍。
3.等分圆周
(1)圆周n等分:以中心角为所对的弦长,依次截取圆周,即可把圆n等分。
(2)圆周四等分:两条互相垂直的直径即可把圆四等分。
(3)圆周六等分:在半径为R的圆上,依次截取等于半径的弦,即可把圆六等分。
周长
若圆的半径是R,则圆的周长=2πR
弧长
若一条弧对的圆心角为n0,半径为R,则弧长l=④_________
考点二 圆的周长和弧长
考点三 扇形的面积
S扇形=⑤___________(R为半径,n为扇形的圆心角度数)。
S扇形=⑥___________(R为半径,l为扇形的弧长)。
考点四 圆锥的侧面积与全面积
图形
简介
圆锥的侧面展开图是扇形。扇形的半径等于圆锥的⑦______,扇形的弧长就是圆锥的底面圆的周长。
侧面积
S圆锥侧=⑧__________________。
全面积
S圆锥全=⑨__________________。
题 型 归 类 探 究
类型一 正多边形和圆(易错点)
【典例1】(2017·达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
【思路导引】首先求出圆内接正三角形、正方形和正六边形的边心距,然后再根据三边长识别三角形的特殊形状,最后利用三角形的面积公式计算求解。
【自主解答】
【方法技巧】进行正多边形的计算的要求:(1)明确正多边形的中心、半径、边心距、中心角的概念;(2)作辅助线:作半径和边心距,把问题转化为解直角三角形的问题来解决。
【变式训练】
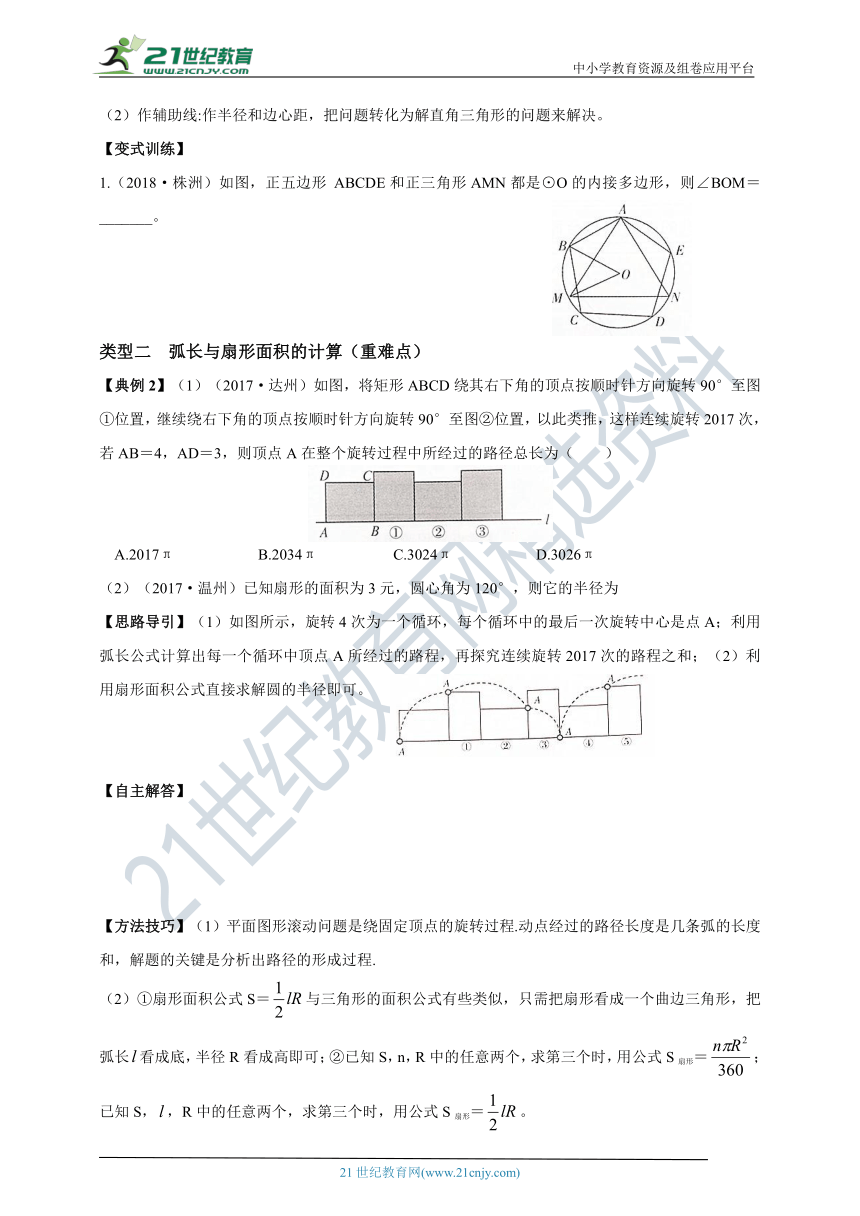
1.(2018·株洲)如图,正五边形 ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=_______。
类型二 弧长与扇形面积的计算(重难点)
【典例2】(1)(2017·达州)如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次,若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
A.2017π B.2034π C.3024π D.3026π
(2)(2017·温州)已知扇形的面积为3元,圆心角为120°,则它的半径为
【思路导引】(1)如图所示,旋转4次为一个循环,每个循环中的最后一次旋转中心是点A;利用弧长公式计算出每一个循环中顶点A所经过的路程,再探究连续旋转2017次的路程之和;(2)利用扇形面积公式直接求解圆的半径即可。
【自主解答】
【方法技巧】(1)平面图形滚动问题是绕固定顶点的旋转过程.动点经过的路径长度是几条弧的长度和,解题的关键是分析出路径的形成过程.
(2)①扇形面积公式S=与三角形的面积公式有些类似,只需把扇形看成一个曲边三角形,把弧长看成底,半径R看成高即可;②已知S,n,R中的任意两个,求第三个时,用公式S扇形=;已知S,,R中的任意两个,求第三个时,用公式S扇形=。
【变式训练】
2.(2018·哈尔滨)一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是_______ cm2。
类型三 阴影面积的计算(高频点)
【典例3】
(2018·十堰)如图,扇形OAB中,∠AOB=100°,OA=12,C是OA的中点,CD⊥OA交弧AB于点D,以OC为半径的弧CE交OB于点E,则图中阴影部分的面积是( )
A.12π+18 B.12π+36 C.6π+18 D.6π+36
【思路导引】
连接OD,易证△OCD是含60°角的直角三角形,于是阴影部分面积。
【自主解答】
【方法技巧】(1)求不规则图形的面积时,要将不规则图形转化为与其面积相等的规则图形求解,或将不规则图形转化为规则图形的面积的和(或差)的形式进行求解。(2)弓形是弦和弦所对的弧所围成的图形,利用扇形面积可求出弓形面积:①当弓形所含的弧是劣弧时,如图1,;②当弓形所含的弧是优弧时,如图2,;③当弓形所含的弧是半圆时,如图3,。
【变式训练】
3.(2018·龙东)如图,在△ABC中,AB=5,AC=3,BC=4,将
△ABC绕点A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为( )
A.π-6 B.π C.π-3 D.+π
类型四 圆锥的有关计算(易错点)
【典例4】(2016·自贡)圆锥的底面半径为4 cm,高为5 cm,则它的表面积为( )
A.12πcm2 B.26π cm2 C.π cm2 D.(4+16)cm2
【思路导引】圆锥的表面积也就是它的全面积,等于底面圆面积与侧面积之和只需利用勾股定理求出圆锥的母线长,然后套用公式直接计算求值即可。
【自主解答】
【方法技巧】圆锥和侧面展开图之间转换的“两个对应”:(1)圆锥的母线与展开后扇形的半径的对应;(2)展开后扇形的弧长与圆锥底面周长的对应。
【变式训练】
4.(2018·仙桃)一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是( )A.120° B.180° C.240° D.300°
中 考 真 题 回 放
考点一 正多边形和圆
1.(2017·滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.2 C. D.1
2.(2018·烟台)如图,点O为正六边形 ABCDEF的中心,点M为AF中点.以点O为圆心、以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心、以DE的长为半径画弧得到扇形DEF.把扇形MON的两条半径OM、ON重合,围成圆锥,将此圆锥的底面半径记为r1,将扇形DEF以同方法围成的圆锥的底面半径记为r2.则r1:r2=_____________。
3.(2018·宜宾)刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S=__________.(结果保留根号)
考点二 弧长
4.(2018·滨州)已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧AC的长为( )
A.π B .π C .π D .
5.(2018·酒泉)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为______________。
6.(2018·潍坊)如图,点A1的坐标为(2,0),过点A1,作x轴的垂线交直线:y=x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2,作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去,则弧A2019B2018的长是_____________。
考点三 阴影面积的计算
7.(2018·德州)如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为( )
A. m2 B. m2
C.πm2 D. 2πm2
8.(2018·威海)如图,正方形ABCD中,AB=12,点E为BC中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
9.(2018·济南)如图1,一扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重叠部分,则阴影部分的面积为( )
B.
C. D.
10.(2018·青岛)如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是_____________。
11.(2017·日照)如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是__________。
考点四 圆锥的有关计算
12.(2018·聊城)用一块圆心角为216°的扇形铁皮,做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是________cm.
13.(2017·聊城)已知圆锥形工件的底面直径是40cm,母线长为30cm,其侧面展开图圆心角的度数为____________。
14.(2017·莱芜)圆锥的底面周长为,母线长为2,点P是母线OA的中点,一根细绳(无弹性)从点P绕圆锥侧面一周回到点P,则细绳的最短长度为_____________。
参考答案及解析
【题型归类探究】
【典例1】
【自主解答】A 解析:如图1,OD=2×sin30°=1;如图2,OE=2×sin45°=;如图3,OD=2×cos30°=.则三角形的三边长为1,,,满足.所以该三角形是直角三角形,其面积为×1×=。
【变式训练】1.48° 解析:连接AO,则有∠AOM=×360°=120°,∠AOB=×360°=72°,∴∠BOM=∠AOM-∠AOB=120°-72°=48°。
【典例2】
【自主解答】(1)D解析:由题意可知,旋转4次是一个循环,其中第4次是绕A点旋转,点A不移动距离,每一个循环,所转过的弧长之和是,2017=4×504+1,因此连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是504×6π+2π=3026π。
(2)3 解析:根据题意,得S扇形=,解得R=3.
【变式训练】 2.6π
【典例3】
【自主解答】 C 解析:连接OD.在Rt△OCD中,cos∠COD=,
∴∠COD=60°,∠BOD=100°-60°=40°。由勾股定理,得CD=。
S阴影=S扇形OBD+S△COD-S扇形OCE=。
【变式训练】3.B 解析:△ABC中,∵AB=5,AC=3,BC=4,∴AC2+BC2=25=AB2,
∴∠ACB=90°,∵△ABC绕点A逆时针方向旋转40°得到△ADE,
∴S△ABC=S△EAD,S阴影=S△EAD+S扇形DAB-S△ABC=S扇形DAB=。
【典例4】
【自主解答】D 解析:圆锥的母线长=(cm),
∴圆锥的侧面积为πr=(cm2);底面圆的面积为16πcm2,
故它的表面积为(4+16)πcm2。
【变式训练】4. B
【中考真题回放】
1.A 2.
3.2 解析:由题意,易知:OE⊥EG,OG为∠FOE的角平分线,即∠EOG=30°,
∴EG=OE× tan30°=,S=12××1×=2。
4.C 5.πa
6. 解析:直线的解析式为y=x,则在Rt△OA1B1中,tan∠A1OB1==,
∴∠A1OB1=60°∵OA1=2,∴OB1=2OA1=4,OA2=OB1=4.
同理可求OA3=8,…,即有OA1=21,OA2=4=22,OA3=8=23,…,OA2019=22019,
∴弧A2019B2018的长是。
7.A
8.C 解析:如图,取CD的中点M,连接AM、EM、DF、CF,MF;
S半圆CFD=πr2=π×62=18π,S△CDF=×12×6=36,
∵点F是半圆的中点、M是CD的中点,故MF垂直CD,所以AD∥MF,
又∵△ADF、△ADM的底相同,高相等,∴S△ADF=S△ADM=×12×6=36.
同理,S△CEF=×6×6=18,∴S阴影部分=S△ADF+S△CEF+S半圆CFD-S△CDF=18π+18。
9.A 解析:如图,连接OD,AD,由折叠性质可知,AD=OD,CD⊥AO.又OA=OD,
则△AOD是等边三角形,∴∠AOD=60°,
在Rt△COD中,OD=6,则OC=3,CD=3,
S阴影=S扇形AOD-S△COD=。
10. 解析:在Rt△ABC中,∵∠B=90°,∠C=30°,∴∠A=60°。
∵OA=OF,∴△OAF是等边三角形,∴∠AOF=60°,∴∠COF=120°。
∵BC与⊙O相切于点E,∴OE⊥BC.在Rt△OCE中,
∠OEC=90°,∠C=30°,OE=2,
∴OC=2×2=4.在Rt△ABC中,∠C=30°,AC=AO+OC=2+4=6,
∴AB=3,BC=AC·cosC=6×=3.如图,设⊙O与AC相交于点D,过O作OG⊥AF于点G,则OG=OA·sinA=2×=.∵S△ABC=×AB×BC=×3×3=,
S△AOF=×AF×OG=×2×=,S扇形DOF,
∴S阴影部分=S△ABC-S△AOF-S扇形DOF=。
6π
50 解析:设扇形铁皮的半径为R cm,圆锥工件的底面半径为r cm,
根据题意得,,解方程组,得,所以扇形铁皮的半径为50cm.
240o 14.1
第3节 圆的有关计算
考 点 知 识 清 单
考点一 正多边形和圆
性质
n个顶点把圆n等分,顺次连接各分点可作出圆的内接正多边形
正多
边形
外心
正多边形①_________________________。
半径
正多边形②_________________________。
中心角
正多边形各边对的③________________________。
边心距
中心到正多边形的一边的距离。
【温馨提示】
1.正n边形的对称性:正n边形是轴对称图形,有n条对称轴,当n是偶数时,它也是中心对称图形,对称中心为正n边形的中心,
2.正n边形的有关计算:
(1)正n边形的内角=;n正n边形的外角=;正n边形的中心角。
(2)正n边形的半径R,边长a,边心距r的数量关系是:。
(3)正n边形的周长,面积S=.
(4)正六边形的边长等于半径,正三角形的边长等于其半径的倍,正方形的边长等于其半径的倍。
3.等分圆周
(1)圆周n等分:以中心角为所对的弦长,依次截取圆周,即可把圆n等分。
(2)圆周四等分:两条互相垂直的直径即可把圆四等分。
(3)圆周六等分:在半径为R的圆上,依次截取等于半径的弦,即可把圆六等分。
周长
若圆的半径是R,则圆的周长=2πR
弧长
若一条弧对的圆心角为n0,半径为R,则弧长l=④_________
考点二 圆的周长和弧长
考点三 扇形的面积
S扇形=⑤___________(R为半径,n为扇形的圆心角度数)。
S扇形=⑥___________(R为半径,l为扇形的弧长)。
考点四 圆锥的侧面积与全面积
图形
简介
圆锥的侧面展开图是扇形。扇形的半径等于圆锥的⑦______,扇形的弧长就是圆锥的底面圆的周长。
侧面积
S圆锥侧=⑧__________________。
全面积
S圆锥全=⑨__________________。
题 型 归 类 探 究
类型一 正多边形和圆(易错点)
【典例1】(2017·达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
【思路导引】首先求出圆内接正三角形、正方形和正六边形的边心距,然后再根据三边长识别三角形的特殊形状,最后利用三角形的面积公式计算求解。
【自主解答】
【方法技巧】进行正多边形的计算的要求:(1)明确正多边形的中心、半径、边心距、中心角的概念;(2)作辅助线:作半径和边心距,把问题转化为解直角三角形的问题来解决。
【变式训练】
1.(2018·株洲)如图,正五边形 ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=_______。
类型二 弧长与扇形面积的计算(重难点)
【典例2】(1)(2017·达州)如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次,若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
A.2017π B.2034π C.3024π D.3026π
(2)(2017·温州)已知扇形的面积为3元,圆心角为120°,则它的半径为
【思路导引】(1)如图所示,旋转4次为一个循环,每个循环中的最后一次旋转中心是点A;利用弧长公式计算出每一个循环中顶点A所经过的路程,再探究连续旋转2017次的路程之和;(2)利用扇形面积公式直接求解圆的半径即可。
【自主解答】
【方法技巧】(1)平面图形滚动问题是绕固定顶点的旋转过程.动点经过的路径长度是几条弧的长度和,解题的关键是分析出路径的形成过程.
(2)①扇形面积公式S=与三角形的面积公式有些类似,只需把扇形看成一个曲边三角形,把弧长看成底,半径R看成高即可;②已知S,n,R中的任意两个,求第三个时,用公式S扇形=;已知S,,R中的任意两个,求第三个时,用公式S扇形=。
【变式训练】
2.(2018·哈尔滨)一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是_______ cm2。
类型三 阴影面积的计算(高频点)
【典例3】
(2018·十堰)如图,扇形OAB中,∠AOB=100°,OA=12,C是OA的中点,CD⊥OA交弧AB于点D,以OC为半径的弧CE交OB于点E,则图中阴影部分的面积是( )
A.12π+18 B.12π+36 C.6π+18 D.6π+36
【思路导引】
连接OD,易证△OCD是含60°角的直角三角形,于是阴影部分面积。
【自主解答】
【方法技巧】(1)求不规则图形的面积时,要将不规则图形转化为与其面积相等的规则图形求解,或将不规则图形转化为规则图形的面积的和(或差)的形式进行求解。(2)弓形是弦和弦所对的弧所围成的图形,利用扇形面积可求出弓形面积:①当弓形所含的弧是劣弧时,如图1,;②当弓形所含的弧是优弧时,如图2,;③当弓形所含的弧是半圆时,如图3,。
【变式训练】
3.(2018·龙东)如图,在△ABC中,AB=5,AC=3,BC=4,将
△ABC绕点A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为( )
A.π-6 B.π C.π-3 D.+π
类型四 圆锥的有关计算(易错点)
【典例4】(2016·自贡)圆锥的底面半径为4 cm,高为5 cm,则它的表面积为( )
A.12πcm2 B.26π cm2 C.π cm2 D.(4+16)cm2
【思路导引】圆锥的表面积也就是它的全面积,等于底面圆面积与侧面积之和只需利用勾股定理求出圆锥的母线长,然后套用公式直接计算求值即可。
【自主解答】
【方法技巧】圆锥和侧面展开图之间转换的“两个对应”:(1)圆锥的母线与展开后扇形的半径的对应;(2)展开后扇形的弧长与圆锥底面周长的对应。
【变式训练】
4.(2018·仙桃)一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是( )A.120° B.180° C.240° D.300°
中 考 真 题 回 放
考点一 正多边形和圆
1.(2017·滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.2 C. D.1
2.(2018·烟台)如图,点O为正六边形 ABCDEF的中心,点M为AF中点.以点O为圆心、以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心、以DE的长为半径画弧得到扇形DEF.把扇形MON的两条半径OM、ON重合,围成圆锥,将此圆锥的底面半径记为r1,将扇形DEF以同方法围成的圆锥的底面半径记为r2.则r1:r2=_____________。
3.(2018·宜宾)刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S=__________.(结果保留根号)
考点二 弧长
4.(2018·滨州)已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧AC的长为( )
A.π B .π C .π D .
5.(2018·酒泉)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为______________。
6.(2018·潍坊)如图,点A1的坐标为(2,0),过点A1,作x轴的垂线交直线:y=x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2,作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去,则弧A2019B2018的长是_____________。
考点三 阴影面积的计算
7.(2018·德州)如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为( )
A. m2 B. m2
C.πm2 D. 2πm2
8.(2018·威海)如图,正方形ABCD中,AB=12,点E为BC中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
9.(2018·济南)如图1,一扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重叠部分,则阴影部分的面积为( )
B.
C. D.
10.(2018·青岛)如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是_____________。
11.(2017·日照)如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是__________。
考点四 圆锥的有关计算
12.(2018·聊城)用一块圆心角为216°的扇形铁皮,做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是________cm.
13.(2017·聊城)已知圆锥形工件的底面直径是40cm,母线长为30cm,其侧面展开图圆心角的度数为____________。
14.(2017·莱芜)圆锥的底面周长为,母线长为2,点P是母线OA的中点,一根细绳(无弹性)从点P绕圆锥侧面一周回到点P,则细绳的最短长度为_____________。
参考答案及解析
【题型归类探究】
【典例1】
【自主解答】A 解析:如图1,OD=2×sin30°=1;如图2,OE=2×sin45°=;如图3,OD=2×cos30°=.则三角形的三边长为1,,,满足.所以该三角形是直角三角形,其面积为×1×=。
【变式训练】1.48° 解析:连接AO,则有∠AOM=×360°=120°,∠AOB=×360°=72°,∴∠BOM=∠AOM-∠AOB=120°-72°=48°。
【典例2】
【自主解答】(1)D解析:由题意可知,旋转4次是一个循环,其中第4次是绕A点旋转,点A不移动距离,每一个循环,所转过的弧长之和是,2017=4×504+1,因此连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是504×6π+2π=3026π。
(2)3 解析:根据题意,得S扇形=,解得R=3.
【变式训练】 2.6π
【典例3】
【自主解答】 C 解析:连接OD.在Rt△OCD中,cos∠COD=,
∴∠COD=60°,∠BOD=100°-60°=40°。由勾股定理,得CD=。
S阴影=S扇形OBD+S△COD-S扇形OCE=。
【变式训练】3.B 解析:△ABC中,∵AB=5,AC=3,BC=4,∴AC2+BC2=25=AB2,
∴∠ACB=90°,∵△ABC绕点A逆时针方向旋转40°得到△ADE,
∴S△ABC=S△EAD,S阴影=S△EAD+S扇形DAB-S△ABC=S扇形DAB=。
【典例4】
【自主解答】D 解析:圆锥的母线长=(cm),
∴圆锥的侧面积为πr=(cm2);底面圆的面积为16πcm2,
故它的表面积为(4+16)πcm2。
【变式训练】4. B
【中考真题回放】
1.A 2.
3.2 解析:由题意,易知:OE⊥EG,OG为∠FOE的角平分线,即∠EOG=30°,
∴EG=OE× tan30°=,S=12××1×=2。
4.C 5.πa
6. 解析:直线的解析式为y=x,则在Rt△OA1B1中,tan∠A1OB1==,
∴∠A1OB1=60°∵OA1=2,∴OB1=2OA1=4,OA2=OB1=4.
同理可求OA3=8,…,即有OA1=21,OA2=4=22,OA3=8=23,…,OA2019=22019,
∴弧A2019B2018的长是。
7.A
8.C 解析:如图,取CD的中点M,连接AM、EM、DF、CF,MF;
S半圆CFD=πr2=π×62=18π,S△CDF=×12×6=36,
∵点F是半圆的中点、M是CD的中点,故MF垂直CD,所以AD∥MF,
又∵△ADF、△ADM的底相同,高相等,∴S△ADF=S△ADM=×12×6=36.
同理,S△CEF=×6×6=18,∴S阴影部分=S△ADF+S△CEF+S半圆CFD-S△CDF=18π+18。
9.A 解析:如图,连接OD,AD,由折叠性质可知,AD=OD,CD⊥AO.又OA=OD,
则△AOD是等边三角形,∴∠AOD=60°,
在Rt△COD中,OD=6,则OC=3,CD=3,
S阴影=S扇形AOD-S△COD=。
10. 解析:在Rt△ABC中,∵∠B=90°,∠C=30°,∴∠A=60°。
∵OA=OF,∴△OAF是等边三角形,∴∠AOF=60°,∴∠COF=120°。
∵BC与⊙O相切于点E,∴OE⊥BC.在Rt△OCE中,
∠OEC=90°,∠C=30°,OE=2,
∴OC=2×2=4.在Rt△ABC中,∠C=30°,AC=AO+OC=2+4=6,
∴AB=3,BC=AC·cosC=6×=3.如图,设⊙O与AC相交于点D,过O作OG⊥AF于点G,则OG=OA·sinA=2×=.∵S△ABC=×AB×BC=×3×3=,
S△AOF=×AF×OG=×2×=,S扇形DOF,
∴S阴影部分=S△ABC-S△AOF-S扇形DOF=。
6π
50 解析:设扇形铁皮的半径为R cm,圆锥工件的底面半径为r cm,
根据题意得,,解方程组,得,所以扇形铁皮的半径为50cm.
240o 14.1
同课章节目录
