6.10 运算律整理与练习 课件(共16张PPT)
文档属性
| 名称 | 6.10 运算律整理与练习 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 673.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-28 17:51:32 | ||
图片预览






文档简介
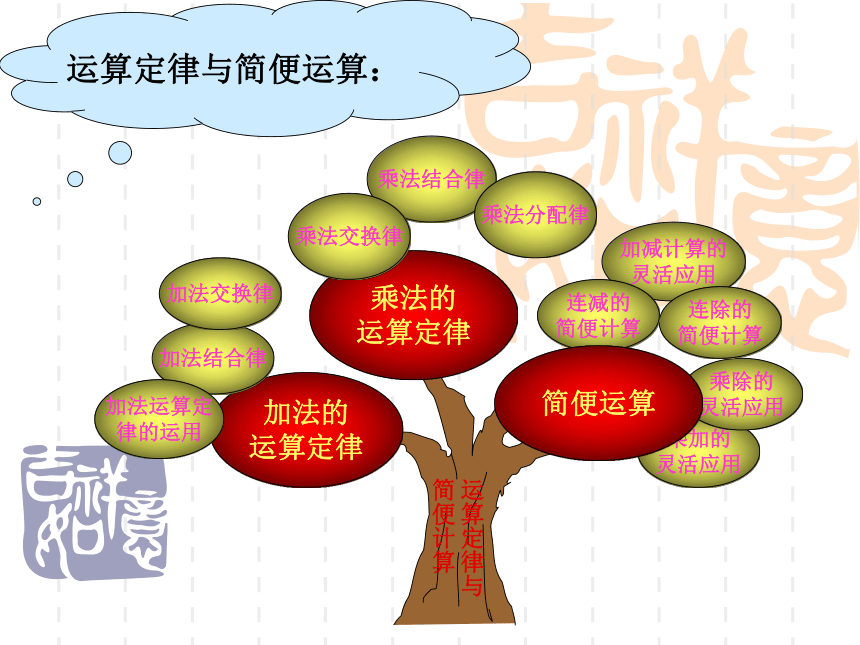
课件16张PPT。 关于运算律…… 《运算律》的整理与练习 一 运算律的基本概念及表示方法加法交换律:加法结合律:概念:字母表示:加法的运算律两个数相加,交换加数的位置,它们的和不变。a+b=b+a概念: 三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。字母表示:(a+b)+c=a+(b+c)一 运算律的基本概念及表示方法加法交换律:加法结合律:概念:字母表示:加法的运算律两个数相加,交换加数的位置,它们的和不变。a+b=b+a概念: 三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。字母表示:(a+b)+c=a+(b+c)乘法交换律:乘法结合律:概念:字母表示:乘法的运算律两个数相乘,交换乘数的位置,它们的积不变。a×b=b×a概念: 三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再同第一个数相乘,它们的积不变。字母表示:(a×b)×c=a×(b×c)乘法分配律:概念:两个数的和乘一个数,可以把它们分别乘这个数,再把积相加,得数不变。字母表示:(a+b)×c=a×c+b×c基本类型:字母表示:语言描述:特殊的运算方法382–43–57= 382–(43+57)a–b–c=a–(b+c) 一个数连续减去两个数,等于这个数减去后两个数的和。基本类型:630÷45÷2= 630÷(45×2)字母表示: a÷b÷c=a÷(b×c)语言描述: 一个数连续除以两个数,等于这个数除以后两个数的积。减法的运算性质:除法的运算性质: a+b = b+a(a+b)+c = a+(b+c) a×b = b×a(a×b)×c = a×(b×c)(a+b)×c=a×c+b×c加法交换律加法结合律乘法交换律乘法结合律乘法分配律运算律名称用字母表示减法的运算性质除法的运算性质运算律的整理与复习(乘法)相乘得整十、整百或整千的数先乘:简便计算小窍门:
44+16= 37+63= 820+180=
2×35= 25×4= 125×8=(加法)相加得整十、整百或整千的数先加:601001000701001000
65+28+35+72=(65+35)+(28+72)
=100+100
=200
25×125×4×8
=(25×4)×(125×8)
=100×1000
=100000运算律的实际应用(一): 528–(150+128) 3200÷25÷4=528–128–150
=400–150
=250=3200÷(25×4)
=3200÷100
=32135×6+65×6 (25+11)×40=(135+65)×6
=200×6
=1200=25×40+11×40
=1000+440
=1440运算律的实际应用(二): 256–198=256–200+2
=56+2
=58 256–203=256–200–3
=56–3
=53 125×32×25=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000 45×102=45×(100+2)
=45×100+45×2
=4500+90
=4590 25×44 =25×(40+4)
=25×40+25×4
=1000+100
=1100 25×44
=25×4×11
=100×11
=1100
256–58+44 250÷8×4
44+16= 37+63= 820+180=
2×35= 25×4= 125×8=(加法)相加得整十、整百或整千的数先加:601001000701001000
65+28+35+72=(65+35)+(28+72)
=100+100
=200
25×125×4×8
=(25×4)×(125×8)
=100×1000
=100000运算律的实际应用(一): 528–(150+128) 3200÷25÷4=528–128–150
=400–150
=250=3200÷(25×4)
=3200÷100
=32135×6+65×6 (25+11)×40=(135+65)×6
=200×6
=1200=25×40+11×40
=1000+440
=1440运算律的实际应用(二): 256–198=256–200+2
=56+2
=58 256–203=256–200–3
=56–3
=53 125×32×25=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000 45×102=45×(100+2)
=45×100+45×2
=4500+90
=4590 25×44 =25×(40+4)
=25×40+25×4
=1000+100
=1100 25×44
=25×4×11
=100×11
=1100
256–58+44 250÷8×4
