2018-2019学年上海市浦东新区华师大二附中高二(下)期中数学试卷解析版
文档属性
| 名称 | 2018-2019学年上海市浦东新区华师大二附中高二(下)期中数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-28 07:09:39 | ||
图片预览


文档简介
2018-2019学年上海市浦东新区华师大二附中高二(下)期中数学试卷
一、填空题:
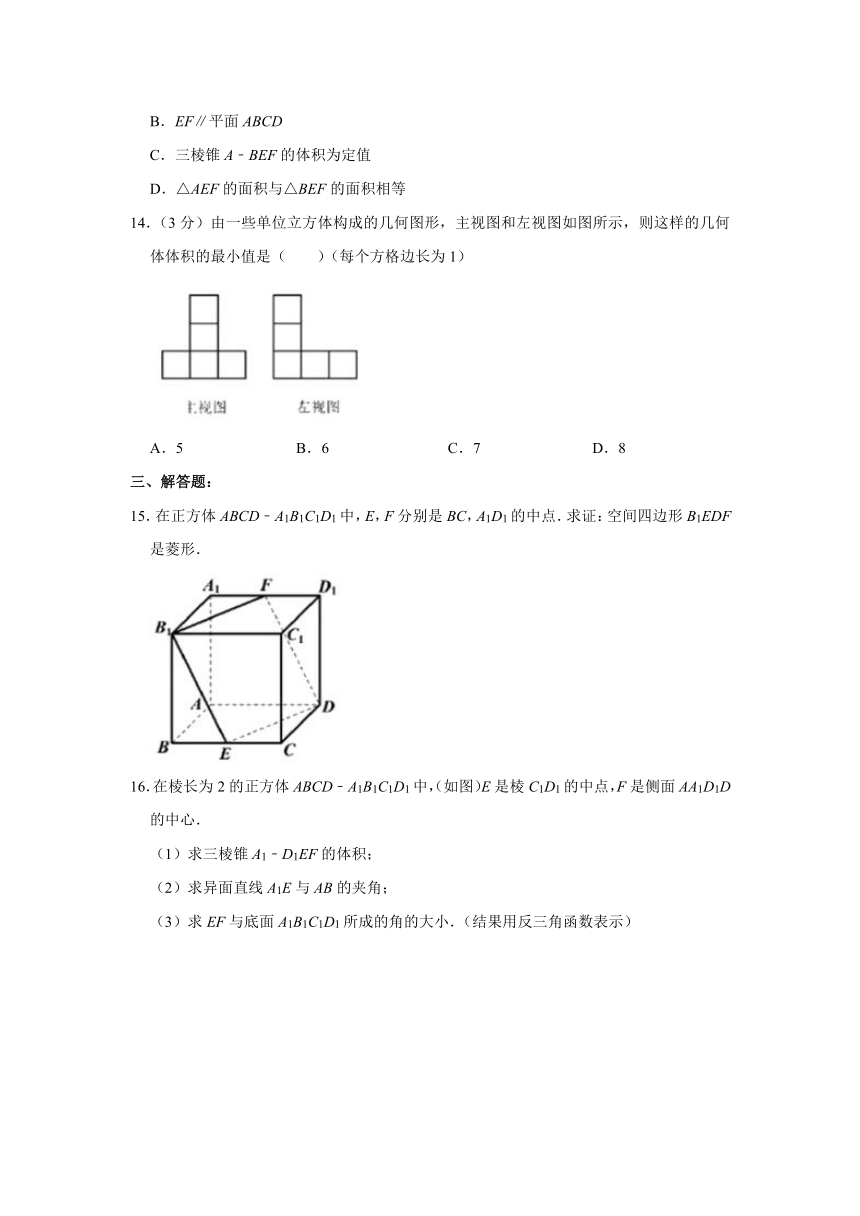
1.(3分)设a,b是平面M外两条直线,且a∥M,那么a∥b是b∥M的 条件.
2.(3分)已知直线a,b及平面α,下列命题中:①;②;③;④.正确命题的序号为 (注:把你认为正确的序号都填上).
3.(3分)地球北纬45°圈上有A,B两地分别在东经80°和170°处,若地球半径为R,则A,B两地的球面距离为 .
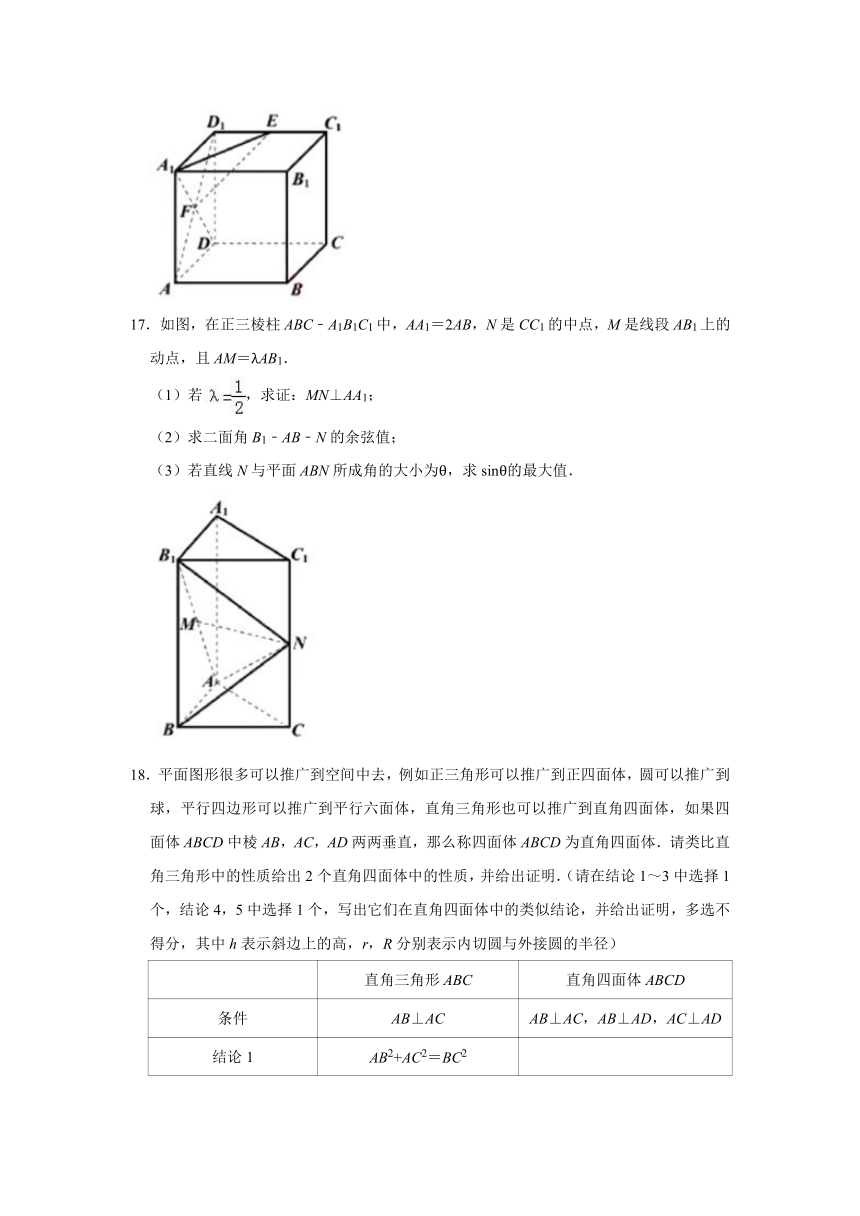
4.(3分)如果一个球和立方体的每条棱都相切,那么称这个球为立方体的棱切球,那么单位立方体的棱切球的体积是 .
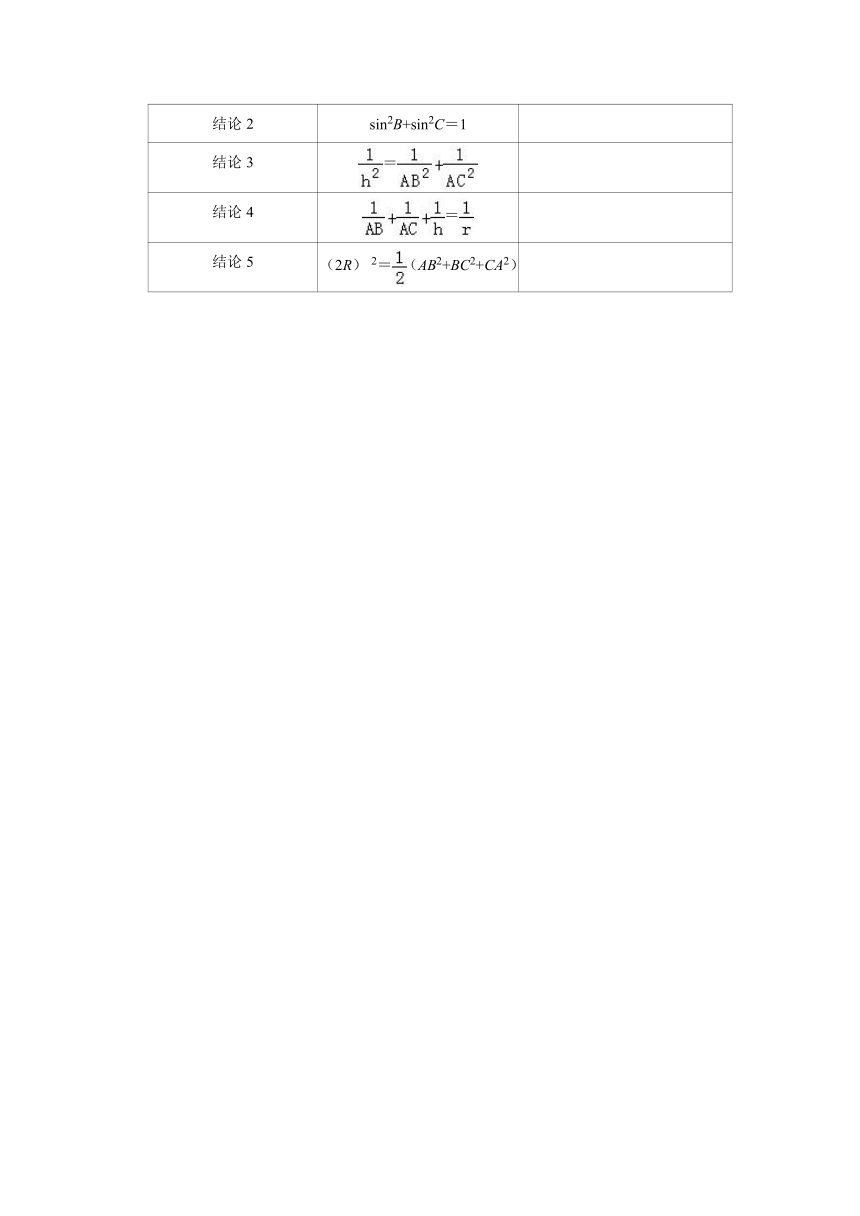
5.(3分)若三棱锥S﹣ABC的所有的顶点都在球O的球面上.SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=,则球O的表面积为 .
6.(3分)如图所示,四棱锥P﹣ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=a,则它的5个面中,互相垂直的面有 对.
7.(3分)如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为 .
8.(3分)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为 .
9.(3分)四面体的6条棱所对应的6个二面角中,钝二面角最多有 个.
10.(3分)在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比=,将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,则类比的结论为 .
二、选择题:
11.(3分)当我们停放自行车时,只要将自行车旁的撑脚放下,自行车就稳了,这用到了( )
A.三点确定一平面
B.不共线三点确定一平面
C.两条相交直线确定一平面
D.两条平行直线确定一平面
12.(3分)正方体被平面所截得的图形不可能是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
13.(3分)如图正方体ABCD﹣A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
14.(3分)由一些单位立方体构成的几何图形,主视图和左视图如图所示,则这样的几何体体积的最小值是( )(每个方格边长为1)
A.5 B.6 C.7 D.8
三、解答题:
15.在正方体ABCD﹣A1B1C1D1中,E,F分别是BC,A1D1的中点.求证:空间四边形B1EDF是菱形.
16.在棱长为2的正方体ABCD﹣A1B1C1D1中,(如图)E是棱C1D1的中点,F是侧面AA1D1D的中心.
(1)求三棱锥A1﹣D1EF的体积;
(2)求异面直线A1E与AB的夹角;
(3)求EF与底面A1B1C1D1所成的角的大小.(结果用反三角函数表示)
17.如图,在正三棱柱ABC﹣A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点,且AM=λAB1.
(1)若,求证:MN⊥AA1;
(2)求二面角B1﹣AB﹣N的余弦值;
(3)若直线N与平面ABN所成角的大小为θ,求sinθ的最大值.
18.平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体ABCD中棱AB,AC,AD两两垂直,那么称四面体ABCD为直角四面体.请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论1~3中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中h表示斜边上的高,r,R分别表示内切圆与外接圆的半径)
直角三角形ABC 直角四面体ABCD
条件 AB⊥AC AB⊥AC,AB⊥AD,AC⊥AD
结论1 AB2+AC2=BC2
结论2 sin2B+sin2C=1
结论3 =
结论4 =
结论5 (2R) 2=(AB2+BC2+CA2)
2018-2019学年上海市浦东新区华师大二附中高二(下)期中数学试卷
参考答案与试题解析
一、填空题:
1.【解答】解:证明充分性:若a∥b,结合a∥M,且b在平面M外,可得b∥M,是充分条件;
证明必要性:若b∥M,结合a∥M,且a,b是平面M外,则a,b可以平行,也可以相交或者异面,所以不是必要条件.
故a∥b是b∥M的“充分不必要”
故答案为:充分不必要.
2.【解答】解:对于①若b⊥α,a⊥b,则a?α或a∥α;
对于②,a⊥b,b∥α则a也可与α平行;
对于③a?α时,不成立;
对于④,根据两条平行线中有一条垂直于平面,则另一条也垂直于平面,故正确
故答案为④.
3.【解答】解:地球表面上从A地(北纬45°,东经80°)到B地(北纬45°,西经170°),
A,B两地都在北纬45°上,对应的纬圆半径是,经度差是90°.
∴AB=R,得球心角是.
∴A,B两地的球面距离是.
故答案为:.
4.【解答】解:球和立方体的每条棱都相切,则球的直径为立方体的面对角线长度,
∴单位立方体的棱切球的半径为,
则球的体积为.
故答案为:.
5.【解答】解:如图,三棱锥S﹣ABC的所有顶点都在球O的球面上,
∵SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=,
∴BC==2,
∴AC2=BC2+AB2,∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=AC=2,
∴球O的半径R==,
∴球O的表面积S=4πR2=20π.
故答案为:20π.
6.【解答】解:底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=a,可得PA⊥底面ABCD
PA?平面PAB,PA?平面PAD,可得:面PAB⊥面ABCD,面PAD⊥面ABCD,AB⊥面PAD,
可得:面PAB⊥面PAD,
BC⊥面PAB,可得:面PAB⊥面PBC,
CD⊥面PAD,可得:面PAD⊥面PCD;
故答案为:5
7.【解答】解:由已知中由一个边长为2的正方形及四个正三角形构成
故该棱锥的底面面积S=2×2=4
侧高为正三角形的高
则棱锥的高h==
故折起后形成的四棱锥的体积V==
故答案为:
8.【解答】解:DC=ABsin 45°=,BC=ABsin 45°+AD=+1,
S梯形ABCD=(AD+BC)DC=(2+)=+,
S=S梯形ABCD=2+.
故答案为:2+
9.【解答】解:将三棱锥的顶点,向下压到与底重合,侧面的3个二面角都是180°,
将这个顶点稍稍提高一点点,离开底面,
此时3个侧面的二面角都是钝角.
故答案为:3.
10.【解答】解:在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比=,
将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,
则类比的结论为根据面积类比体积,长度类比面积可得:,
故答案为:.
二、选择题:
11.【解答】解:自行车前后轮与撑脚分别接触地面,此时三个接触点不在同一条线上,
所以可以确定一个平面,即地面,从而使得自行车稳定.
故选:B.
12.【解答】解:如图所示,平面与正方体相交与不同的位置,可以出现正三角形,正方形,正六边形,不可能出现正五边形,
.
故选:C.
13.【解答】解:连结BD,则AC⊥平面BB1D1D,BD∥B1D1,
∴AC⊥BE,EF∥平面ABCD,三棱锥A﹣BEF的体积为定值,
从而A,B,C正确.
∵点A、B到直线B1D1的距离不相等,
∴△AEF的面积与△BEF的面积不相等,
故D错误.
故选:D.
14.【解答】解:通过主视图和左视图分析出原几何体的形状如图所示,可知最少共有7个单位立方体.
则几何体的体积最小值为7.
故选:C.
三、解答题:
15.【解答】
证明:取AD中点G,连接FG,BG,可得B1B∥FG,B1B=FG,
∴四边形B1BGF为平行四边形,则BG∥B1F,
由ABCD﹣A1B1C1D1为正方体,且E,G分别为BC,AD的中点,
可得BEDG为平行四边形,∴BG∥DE,BG=DE,
则B1F∥DE,且B1F=DE,
∴四边形B1EDF为平行四边形,由△B1BE≌△B1A1F,可得B1E=B1F,
∴四边形B1EDF是菱形;.
16.【解答】解:(1)由题意知,==??h=×(×2×1)×1=;
(2)∵A1B1∥AB,∴∠EA1B1或其补角即为异面直线A1E与AB所成角,
在△EA1B1,A1E=EB1=,A1B1=2,
∴cos∠EA1B1===,
∴异面直线A1E与AB所成角为arccos;
(3)取A1D1中点M,联结MF,
∵MF∥A1A且A1A⊥平面A1B1C1D1,∴MF⊥平面A1B1C1D1,
∴∠FEM即为EF与底面A1B1C1D1所成的角,
MF=AA1=1,ME=
∴tan∠FEM===,
∴EF与底面A1B1C1D1所成的角的大小为arctan.
17.【解答】解:(1)取AA1中点D,联结MD和ND,
∵λ=,∴M为AB1中点,又D为AA1中点,∴MD∥B1A1,
∵B1A1⊥AA1,∴MD⊥AA1,
同理ND⊥AA1,∴AA1⊥平面MND,∴MN⊥AA1;
(2)取AB中点E,A1B1中点F,联结EN、EF、FN,
则EN⊥AB,EF⊥AB,∠FEN即为二面角B1﹣AB﹣N的平面角,
设AB=2a(a>0),则EF=4a,EN=FN=a,
∴cos∠FEN==,
即二面角B1﹣AB﹣N的余弦值为;
(3)设AB=2a(a>0),M到平面ABN的距离为d,
则S△ABM=λ=λ??2a?4a=4λa2,
S△ABN=?2a?a=a2;
由等体积法,V三棱锥N﹣ABM=V三棱锥M﹣ABN,即?S△ABM?a=?S△ABM?d,
可得d=λa,
而MN==2a,
∴sinθ==?=?=?≤?=,
当且仅当=,即λ=时,等号成立,
即sinθ的最大值为.
18.【解答】解:记△ABC、△ABD、△ACD、△BCD的面积依次为S1、S2、S3、S,
平面BCD与AB、AC、AD所成角依次为α、β、γ,
点A到平面BCD的距离为d,r,R分别表示内切球与外接球的半径,内切球的球心为O,
直角三角形ABC 直角四面体ABCD
条件 AB⊥AC AB⊥AC,AB⊥AD,AC⊥AD
结论1 AB2+AC2=BC2
结论2 sin2B+sin2C=1 sin2α+sin2β+sin2γ=1
结论3 =
结论4 =
结论5 (2R) 2=(AB2+BC2+CA2) (2R)2=AB2+AC2+BC2
证明:设AB=a、AC=b、AD=c,
过A作AE⊥BC,垂足为E,联结DE,过A作AH⊥DE,垂足为H,
易证:DE⊥BC,AH⊥平面BCD,则d=AH,
结论1:==,
在Rt△ABC中,AE=.DE==,
=
∴;
结论2:d=AH===,
∴sinα==.同理,sinβ=,sinγ=,
∴sin2α+sin2β+sin2γ==1;
结论3:∵d=,∴=,
又==,
∴
结论4:∵VD﹣ABC=VO﹣ABC+VOABD+VO﹣ACD+VO﹣BCD,
∴=+.
从而=,即;
结论5:将直角四面体ABCD补形成为以AB、AC、AD为长、宽、高的长方体,
则长方体的体对角线即为直角四面体ABCD的外接球的直径,即(2R)2=AB2+BC2+CA2.
一、填空题:
1.(3分)设a,b是平面M外两条直线,且a∥M,那么a∥b是b∥M的 条件.
2.(3分)已知直线a,b及平面α,下列命题中:①;②;③;④.正确命题的序号为 (注:把你认为正确的序号都填上).
3.(3分)地球北纬45°圈上有A,B两地分别在东经80°和170°处,若地球半径为R,则A,B两地的球面距离为 .
4.(3分)如果一个球和立方体的每条棱都相切,那么称这个球为立方体的棱切球,那么单位立方体的棱切球的体积是 .
5.(3分)若三棱锥S﹣ABC的所有的顶点都在球O的球面上.SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=,则球O的表面积为 .
6.(3分)如图所示,四棱锥P﹣ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=a,则它的5个面中,互相垂直的面有 对.
7.(3分)如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为 .
8.(3分)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为 .
9.(3分)四面体的6条棱所对应的6个二面角中,钝二面角最多有 个.
10.(3分)在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比=,将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,则类比的结论为 .
二、选择题:
11.(3分)当我们停放自行车时,只要将自行车旁的撑脚放下,自行车就稳了,这用到了( )
A.三点确定一平面
B.不共线三点确定一平面
C.两条相交直线确定一平面
D.两条平行直线确定一平面
12.(3分)正方体被平面所截得的图形不可能是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
13.(3分)如图正方体ABCD﹣A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
14.(3分)由一些单位立方体构成的几何图形,主视图和左视图如图所示,则这样的几何体体积的最小值是( )(每个方格边长为1)
A.5 B.6 C.7 D.8
三、解答题:
15.在正方体ABCD﹣A1B1C1D1中,E,F分别是BC,A1D1的中点.求证:空间四边形B1EDF是菱形.
16.在棱长为2的正方体ABCD﹣A1B1C1D1中,(如图)E是棱C1D1的中点,F是侧面AA1D1D的中心.
(1)求三棱锥A1﹣D1EF的体积;
(2)求异面直线A1E与AB的夹角;
(3)求EF与底面A1B1C1D1所成的角的大小.(结果用反三角函数表示)
17.如图,在正三棱柱ABC﹣A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点,且AM=λAB1.
(1)若,求证:MN⊥AA1;
(2)求二面角B1﹣AB﹣N的余弦值;
(3)若直线N与平面ABN所成角的大小为θ,求sinθ的最大值.
18.平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体ABCD中棱AB,AC,AD两两垂直,那么称四面体ABCD为直角四面体.请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论1~3中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中h表示斜边上的高,r,R分别表示内切圆与外接圆的半径)
直角三角形ABC 直角四面体ABCD
条件 AB⊥AC AB⊥AC,AB⊥AD,AC⊥AD
结论1 AB2+AC2=BC2
结论2 sin2B+sin2C=1
结论3 =
结论4 =
结论5 (2R) 2=(AB2+BC2+CA2)
2018-2019学年上海市浦东新区华师大二附中高二(下)期中数学试卷
参考答案与试题解析
一、填空题:
1.【解答】解:证明充分性:若a∥b,结合a∥M,且b在平面M外,可得b∥M,是充分条件;
证明必要性:若b∥M,结合a∥M,且a,b是平面M外,则a,b可以平行,也可以相交或者异面,所以不是必要条件.
故a∥b是b∥M的“充分不必要”
故答案为:充分不必要.
2.【解答】解:对于①若b⊥α,a⊥b,则a?α或a∥α;
对于②,a⊥b,b∥α则a也可与α平行;
对于③a?α时,不成立;
对于④,根据两条平行线中有一条垂直于平面,则另一条也垂直于平面,故正确
故答案为④.
3.【解答】解:地球表面上从A地(北纬45°,东经80°)到B地(北纬45°,西经170°),
A,B两地都在北纬45°上,对应的纬圆半径是,经度差是90°.
∴AB=R,得球心角是.
∴A,B两地的球面距离是.
故答案为:.
4.【解答】解:球和立方体的每条棱都相切,则球的直径为立方体的面对角线长度,
∴单位立方体的棱切球的半径为,
则球的体积为.
故答案为:.
5.【解答】解:如图,三棱锥S﹣ABC的所有顶点都在球O的球面上,
∵SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=,
∴BC==2,
∴AC2=BC2+AB2,∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=AC=2,
∴球O的半径R==,
∴球O的表面积S=4πR2=20π.
故答案为:20π.
6.【解答】解:底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=a,可得PA⊥底面ABCD
PA?平面PAB,PA?平面PAD,可得:面PAB⊥面ABCD,面PAD⊥面ABCD,AB⊥面PAD,
可得:面PAB⊥面PAD,
BC⊥面PAB,可得:面PAB⊥面PBC,
CD⊥面PAD,可得:面PAD⊥面PCD;
故答案为:5
7.【解答】解:由已知中由一个边长为2的正方形及四个正三角形构成
故该棱锥的底面面积S=2×2=4
侧高为正三角形的高
则棱锥的高h==
故折起后形成的四棱锥的体积V==
故答案为:
8.【解答】解:DC=ABsin 45°=,BC=ABsin 45°+AD=+1,
S梯形ABCD=(AD+BC)DC=(2+)=+,
S=S梯形ABCD=2+.
故答案为:2+
9.【解答】解:将三棱锥的顶点,向下压到与底重合,侧面的3个二面角都是180°,
将这个顶点稍稍提高一点点,离开底面,
此时3个侧面的二面角都是钝角.
故答案为:3.
10.【解答】解:在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比=,
将这个结论类比到空间:在三棱锥A﹣BCD中,平面DEC平分二面角A﹣CD﹣B且与AB交于E,
则类比的结论为根据面积类比体积,长度类比面积可得:,
故答案为:.
二、选择题:
11.【解答】解:自行车前后轮与撑脚分别接触地面,此时三个接触点不在同一条线上,
所以可以确定一个平面,即地面,从而使得自行车稳定.
故选:B.
12.【解答】解:如图所示,平面与正方体相交与不同的位置,可以出现正三角形,正方形,正六边形,不可能出现正五边形,
.
故选:C.
13.【解答】解:连结BD,则AC⊥平面BB1D1D,BD∥B1D1,
∴AC⊥BE,EF∥平面ABCD,三棱锥A﹣BEF的体积为定值,
从而A,B,C正确.
∵点A、B到直线B1D1的距离不相等,
∴△AEF的面积与△BEF的面积不相等,
故D错误.
故选:D.
14.【解答】解:通过主视图和左视图分析出原几何体的形状如图所示,可知最少共有7个单位立方体.
则几何体的体积最小值为7.
故选:C.
三、解答题:
15.【解答】
证明:取AD中点G,连接FG,BG,可得B1B∥FG,B1B=FG,
∴四边形B1BGF为平行四边形,则BG∥B1F,
由ABCD﹣A1B1C1D1为正方体,且E,G分别为BC,AD的中点,
可得BEDG为平行四边形,∴BG∥DE,BG=DE,
则B1F∥DE,且B1F=DE,
∴四边形B1EDF为平行四边形,由△B1BE≌△B1A1F,可得B1E=B1F,
∴四边形B1EDF是菱形;.
16.【解答】解:(1)由题意知,==??h=×(×2×1)×1=;
(2)∵A1B1∥AB,∴∠EA1B1或其补角即为异面直线A1E与AB所成角,
在△EA1B1,A1E=EB1=,A1B1=2,
∴cos∠EA1B1===,
∴异面直线A1E与AB所成角为arccos;
(3)取A1D1中点M,联结MF,
∵MF∥A1A且A1A⊥平面A1B1C1D1,∴MF⊥平面A1B1C1D1,
∴∠FEM即为EF与底面A1B1C1D1所成的角,
MF=AA1=1,ME=
∴tan∠FEM===,
∴EF与底面A1B1C1D1所成的角的大小为arctan.
17.【解答】解:(1)取AA1中点D,联结MD和ND,
∵λ=,∴M为AB1中点,又D为AA1中点,∴MD∥B1A1,
∵B1A1⊥AA1,∴MD⊥AA1,
同理ND⊥AA1,∴AA1⊥平面MND,∴MN⊥AA1;
(2)取AB中点E,A1B1中点F,联结EN、EF、FN,
则EN⊥AB,EF⊥AB,∠FEN即为二面角B1﹣AB﹣N的平面角,
设AB=2a(a>0),则EF=4a,EN=FN=a,
∴cos∠FEN==,
即二面角B1﹣AB﹣N的余弦值为;
(3)设AB=2a(a>0),M到平面ABN的距离为d,
则S△ABM=λ=λ??2a?4a=4λa2,
S△ABN=?2a?a=a2;
由等体积法,V三棱锥N﹣ABM=V三棱锥M﹣ABN,即?S△ABM?a=?S△ABM?d,
可得d=λa,
而MN==2a,
∴sinθ==?=?=?≤?=,
当且仅当=,即λ=时,等号成立,
即sinθ的最大值为.
18.【解答】解:记△ABC、△ABD、△ACD、△BCD的面积依次为S1、S2、S3、S,
平面BCD与AB、AC、AD所成角依次为α、β、γ,
点A到平面BCD的距离为d,r,R分别表示内切球与外接球的半径,内切球的球心为O,
直角三角形ABC 直角四面体ABCD
条件 AB⊥AC AB⊥AC,AB⊥AD,AC⊥AD
结论1 AB2+AC2=BC2
结论2 sin2B+sin2C=1 sin2α+sin2β+sin2γ=1
结论3 =
结论4 =
结论5 (2R) 2=(AB2+BC2+CA2) (2R)2=AB2+AC2+BC2
证明:设AB=a、AC=b、AD=c,
过A作AE⊥BC,垂足为E,联结DE,过A作AH⊥DE,垂足为H,
易证:DE⊥BC,AH⊥平面BCD,则d=AH,
结论1:==,
在Rt△ABC中,AE=.DE==,
=
∴;
结论2:d=AH===,
∴sinα==.同理,sinβ=,sinγ=,
∴sin2α+sin2β+sin2γ==1;
结论3:∵d=,∴=,
又==,
∴
结论4:∵VD﹣ABC=VO﹣ABC+VOABD+VO﹣ACD+VO﹣BCD,
∴=+.
从而=,即;
结论5:将直角四面体ABCD补形成为以AB、AC、AD为长、宽、高的长方体,
则长方体的体对角线即为直角四面体ABCD的外接球的直径,即(2R)2=AB2+BC2+CA2.
同课章节目录
