沪科版九年级(下册)数学:24.3《圆周角》教学课件 (共46张PPT)
文档属性
| 名称 | 沪科版九年级(下册)数学:24.3《圆周角》教学课件 (共46张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-28 00:00:00 | ||
图片预览



文档简介
沪科版九年级(下册)数学:24.3《圆周角》
一. 复习引入:
1.圆心角的定义?
在同圆(或等圆)中,如果圆心角、弧、弦、弦心距有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四个量之间关系的一个结论,这个结论是什么?
探索1:
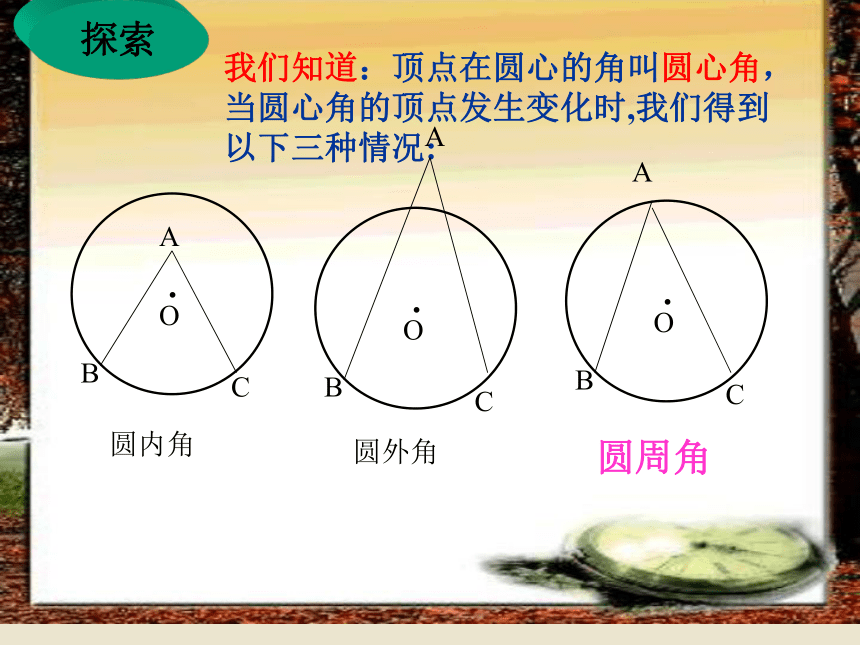
我们知道:顶点在圆心的角叫圆心角,当圆心角的顶点发生变化时,我们得到以下三种情况:
A
.
O
B
C
A
A
圆内角
圆外角
圆周角
探索
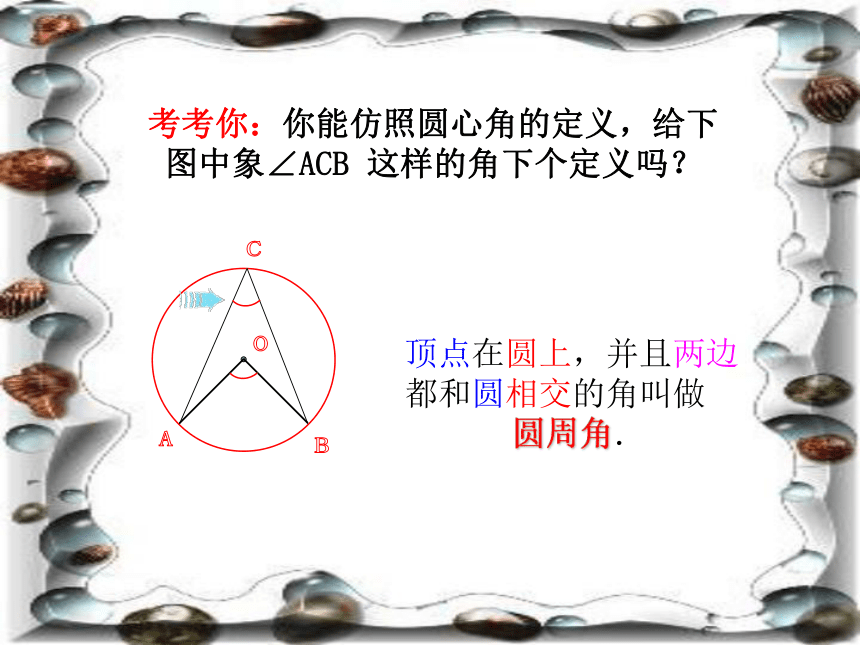
考考你:你能仿照圆心角的定义,给下 图中象∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边都和圆相交的角叫做
圆周角.
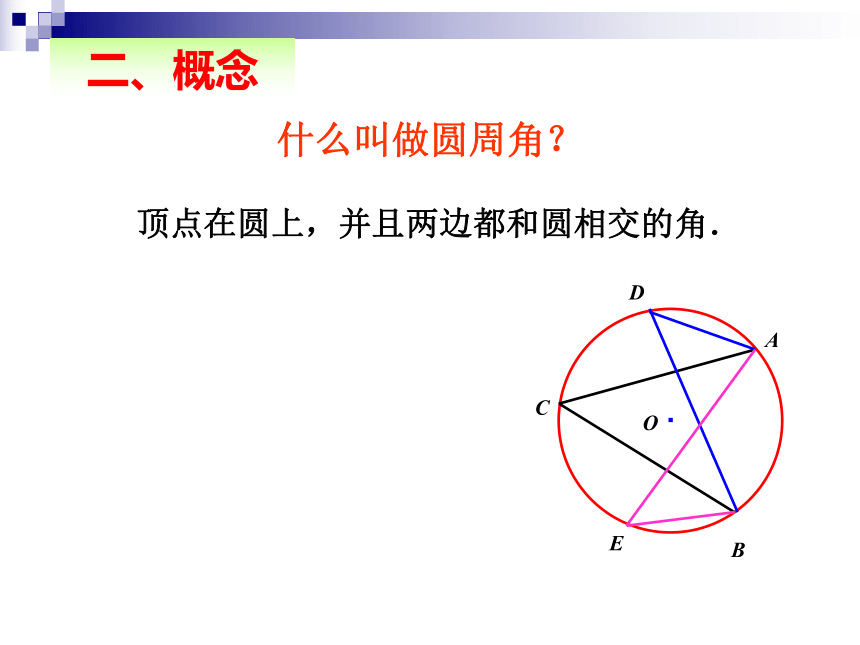
顶点在圆上,并且两边都和圆相交的角.
什么叫做圆周角?
·
A
B
C
O
二、概念
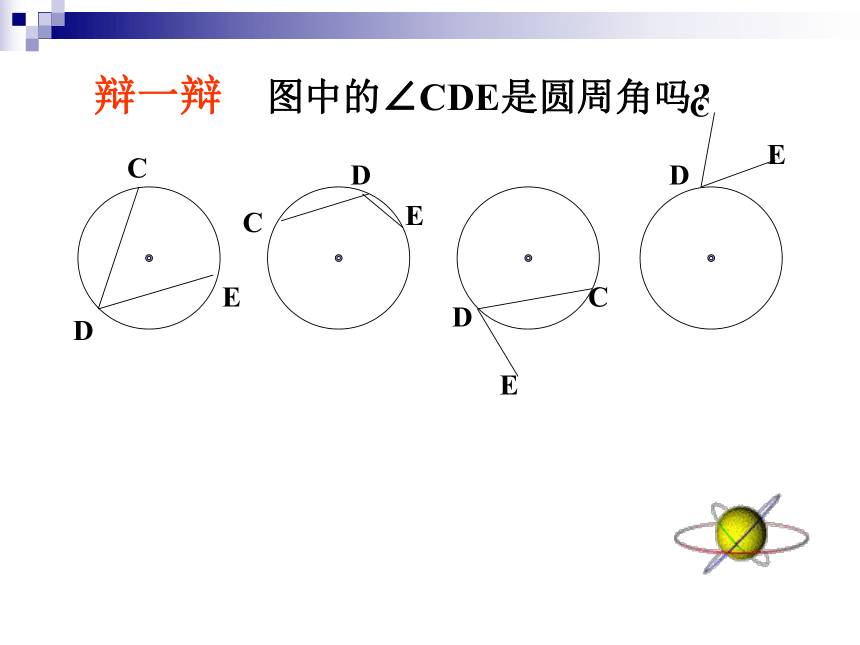
辩一辩 图中的∠CDE是圆周角吗?
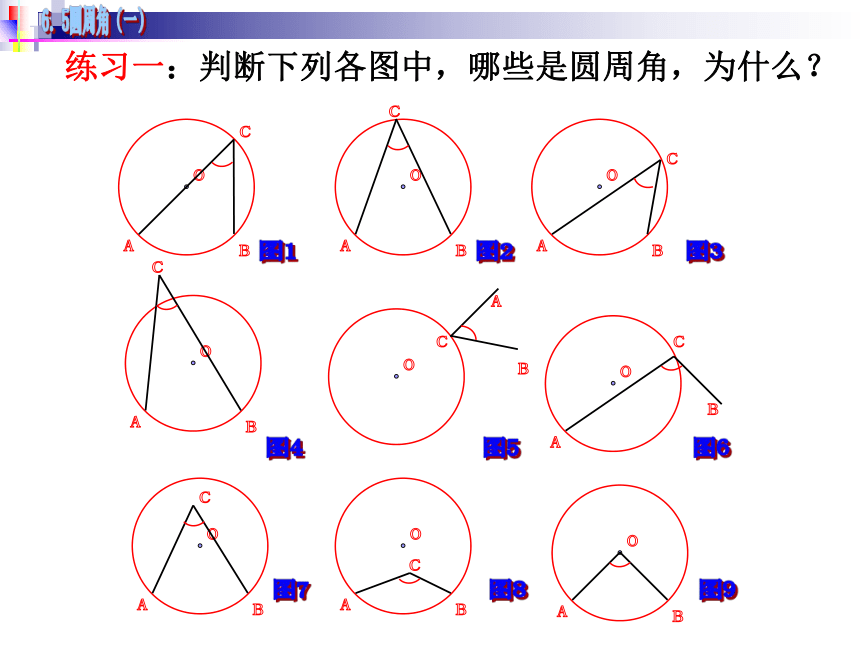
练习一:判断下列各图中,哪些是圆周角,为什么?
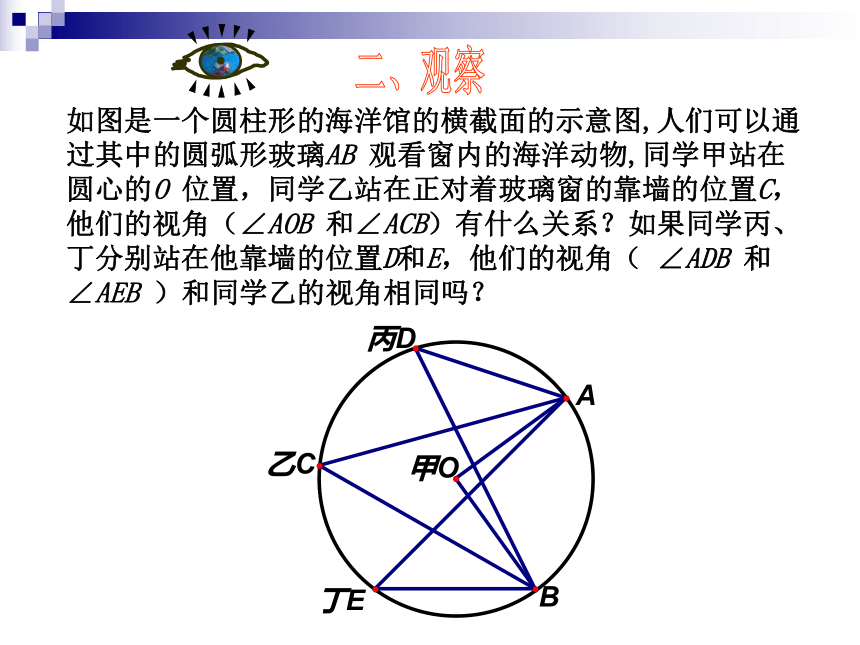
如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和∠AEB )和同学乙的视角相同吗?
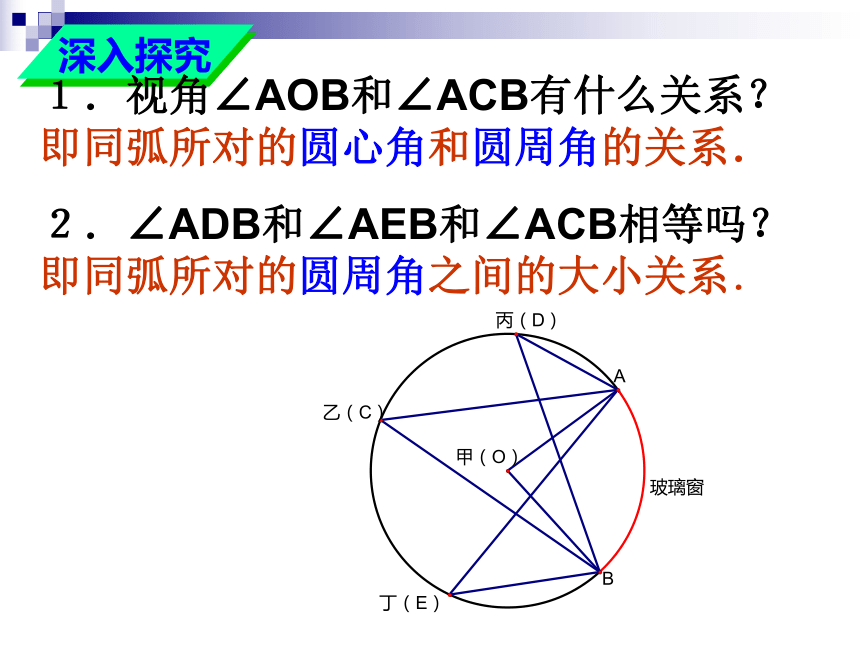
1.视角∠AOB和∠ACB有什么关系?即同弧所对的圆心角和圆周角的关系.
2.∠ADB和∠AEB和∠ACB相等吗?即同弧所对的圆周角之间的大小关系.
类比圆心角探知圆周角
在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
圆周角和圆心角的关系
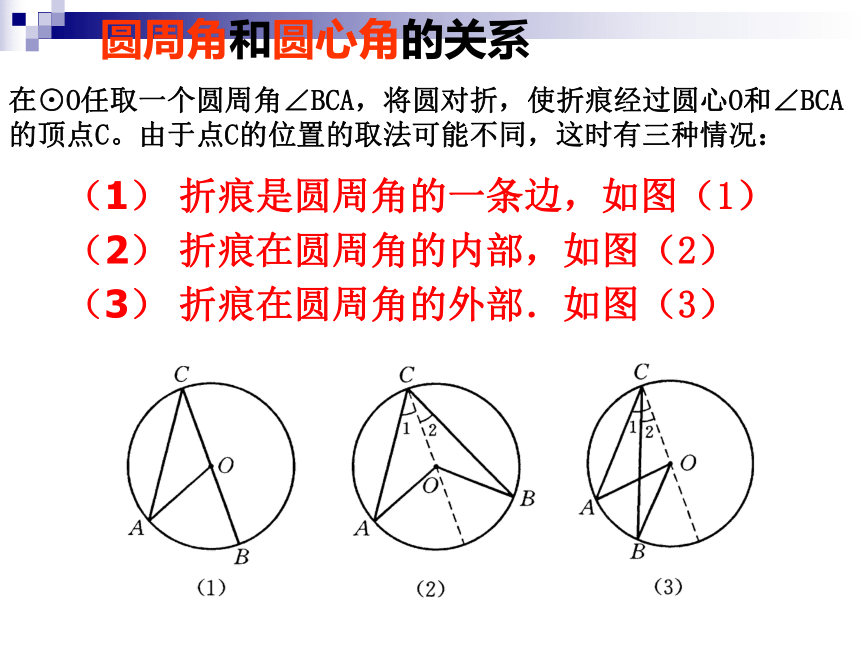
在⊙O任取一个圆周角∠BCA,将圆对折,使折痕经过圆心O和∠BCA的顶点C。由于点C的位置的取法可能不同,这时有三种情况:
(1) 折痕是圆周角的一条边,如图(1)
(2) 折痕在圆周角的内部,如图(2)
(3) 折痕在圆周角的外部.如图(3)
圆周角和圆心角的关系
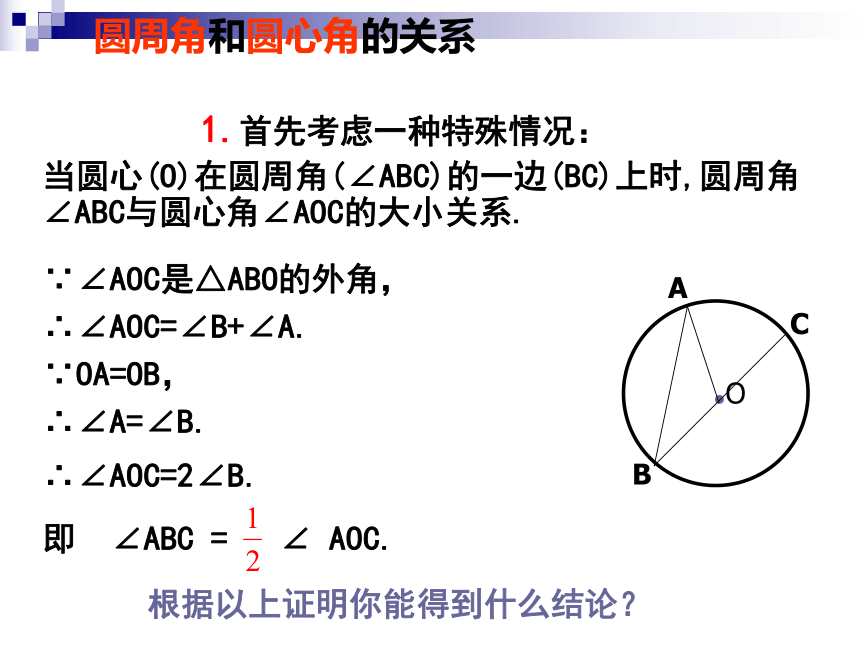
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
根据以上证明你能得到什么结论?
2.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
能否转化为1的情况?
过点B作直径BD.由1可得:
根据以上证明你又能得到什么结论?
圆周角和圆心角的关系
圆周角和圆心角的关系
3.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
能否也转化为1的情况?
过点B作直径BD.由1可得:
根据以上证明你又能得到什么结论?
三.圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
思考:在同圆或等圆中,如果圆周角相等,所对的弧一定相等吗?
弧等
角等
结 论:
如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1=∠4
∠2=∠7
∠3=∠6
∠5=∠8
★
★
★
★
★
★
★
★
思 考
如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?
90°的圆周角所对的弦是什么?
·
A
B
C1
O
C2
C3
定理
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵ ∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°,
∴∠BAD+∠BCD=
180°.
同理∠ABC+∠ADC=180°.
圆内接四边形的对角互补.
圆的内接四边形
如果延长BC到E,那么
∠DCE+∠BCD =
180°.
∴∠A=∠DCE.
又 ∵∠A +∠BCD= 180°,
圆的内接四边形
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.
圆内接四边形的一个外角等于它的内对角.
试金石:
2.如图,圆心角∠AOB=100°,则∠ACB=___。
1.求圆中角X的度数
C
3、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
40°
4.如图:OA、OB、OC都是⊙O的半径,且∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
5⑴如图5,求∠1+∠2+∠3+∠4+∠5= 。
⑵如图6:已知弦AB、CD相交于P点,且∠AOC=44、 ∠BOD=46 求 ∠APC 的度数。
例1 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
四、例题
求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴ △ABC 为直角三角形.
练 习
∠BOC =140°
350
700
1.ΔABC内接于⊙O ,∠BOC=80?,
则∠BAC等于( ).
(A)80? (B) 40? (C) 140? (D) 40?或140?
D
2.已知:如图,AB=AC=AD, ∠BAC=40?,
则∠BDC的度数为( )
(A)40? (B)30?
(C)20? (D)不能确定
C
15°或 75 °
4.如图,⊙O1、⊙O2相交于A、B两点,
直线O1O2交两圆于C、D∠O1AO2=40°,
则∠CBD等于( )
(A)110° (B)120°
(C)130° (D)140°
A
1.如图,已知圆心角∠BOC=100°,
则圆周角∠BAC的度数为( )
A、100° B、130°
C、50° D、80°
2.圆内接正三角形的一条边所对的圆周角为( )
A、30° B、60°
C、30°或150° D、60°或120°
3.如图,A、B、C三点在⊙O上,
∠AOC=100°,则∠ABC等于( )
A、140° B、110°
C、120° D、130°
C
D
D
4.若圆的一条弦把圆分成度数的比为1∶3的两条弧,
则劣弧所对的圆周角的度数为( )
A、45° B、90° C、135° D、270°
5.已知:如图,△ABC内接于
⊙O,AD是⊙O的直径,∠ABC
=30°,则∠CAD等于_________。
6. 在⊙O中,一条弦的长度等
于半径,则它所对的圆周角的
度数为_________。
7.半径为1的圆中有一条弦,如果
它的长为
那么这条弦所对的圆
A
周角的度数等于 .
60°
60°或120 °
30°或150 °
弦AB分圆为l∶5两部分,则弦AB所对
的圆周角度数等于
9. 已知:如图,AB 为⊙O的直径,∠BED=35?,
则∠ACD= ? 。
10.圆内接四边形相邻三个内角之比是3:1:6,
则这个四边形的最大角的度数为 。
30°或150 °
55
160 °
7 学以致用 作业适量 分层要求
A层(基础题)
⑶如图9,已知AB=AC=2cm, ∠BDC=60,则△ABC 的周长是 。
⑷如图10:∠A是⊙O的圆周角,∠A=40°,求∠OBC 的度数。
7 学以致用 作业适量 分层要求
B层(中等题)
⑴ 在⊙O中,∠BOC=100o,则弦BC所对的圆周角
是 度。
⑵如图11,AD是⊙O直径,BC=CD,∠A=30°,
求∠B的度数。
7 学以致用 作业适量 分层要求
C层(提高题)
如图12,AB是⊙O直径,点C在圆上,∠BAC的平分线交圆于点E,OE交BC于点H,已知AC=6,AB=10,求HE的长。
7 学以致用 作业适量 分层要求
D层(课外延拓、承上启下)
如图13:“世界杯”赛场上李铁、邵佳一、郝海东三名队员互相配合向对方球门进攻,当李带球冲到如图C点时,邵、郝也分别跟随冲到图中的D点、E点,李应把球传给谁好?请你从数学角度帮忙合情说理、分析说明。
球门
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
2、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
⌒
⌒
4、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_ _;
20°
25°
3、若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于多少度。
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
四边形与圆的位置关系
如果四边形的四个顶点在一个圆上,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.
我们可以证明圆内接四边的两个重要性质:
1.圆内接四边形对角互补.
2.圆内接四边形对的一个外角等于它的内对角.
一. 复习引入:
1.圆心角的定义?
在同圆(或等圆)中,如果圆心角、弧、弦、弦心距有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四个量之间关系的一个结论,这个结论是什么?
探索1:
我们知道:顶点在圆心的角叫圆心角,当圆心角的顶点发生变化时,我们得到以下三种情况:
A
.
O
B
C
A
A
圆内角
圆外角
圆周角
探索
考考你:你能仿照圆心角的定义,给下 图中象∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边都和圆相交的角叫做
圆周角.
顶点在圆上,并且两边都和圆相交的角.
什么叫做圆周角?
·
A
B
C
O
二、概念
辩一辩 图中的∠CDE是圆周角吗?
练习一:判断下列各图中,哪些是圆周角,为什么?
如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和∠AEB )和同学乙的视角相同吗?
1.视角∠AOB和∠ACB有什么关系?即同弧所对的圆心角和圆周角的关系.
2.∠ADB和∠AEB和∠ACB相等吗?即同弧所对的圆周角之间的大小关系.
类比圆心角探知圆周角
在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
圆周角和圆心角的关系
在⊙O任取一个圆周角∠BCA,将圆对折,使折痕经过圆心O和∠BCA的顶点C。由于点C的位置的取法可能不同,这时有三种情况:
(1) 折痕是圆周角的一条边,如图(1)
(2) 折痕在圆周角的内部,如图(2)
(3) 折痕在圆周角的外部.如图(3)
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
根据以上证明你能得到什么结论?
2.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
能否转化为1的情况?
过点B作直径BD.由1可得:
根据以上证明你又能得到什么结论?
圆周角和圆心角的关系
圆周角和圆心角的关系
3.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
能否也转化为1的情况?
过点B作直径BD.由1可得:
根据以上证明你又能得到什么结论?
三.圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
思考:在同圆或等圆中,如果圆周角相等,所对的弧一定相等吗?
弧等
角等
结 论:
如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1=∠4
∠2=∠7
∠3=∠6
∠5=∠8
★
★
★
★
★
★
★
★
思 考
如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?
90°的圆周角所对的弦是什么?
·
A
B
C1
O
C2
C3
定理
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵ ∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°,
∴∠BAD+∠BCD=
180°.
同理∠ABC+∠ADC=180°.
圆内接四边形的对角互补.
圆的内接四边形
如果延长BC到E,那么
∠DCE+∠BCD =
180°.
∴∠A=∠DCE.
又 ∵∠A +∠BCD= 180°,
圆的内接四边形
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.
圆内接四边形的一个外角等于它的内对角.
试金石:
2.如图,圆心角∠AOB=100°,则∠ACB=___。
1.求圆中角X的度数
C
3、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
40°
4.如图:OA、OB、OC都是⊙O的半径,且∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
5⑴如图5,求∠1+∠2+∠3+∠4+∠5= 。
⑵如图6:已知弦AB、CD相交于P点,且∠AOC=44、 ∠BOD=46 求 ∠APC 的度数。
例1 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
四、例题
求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴ △ABC 为直角三角形.
练 习
∠BOC =140°
350
700
1.ΔABC内接于⊙O ,∠BOC=80?,
则∠BAC等于( ).
(A)80? (B) 40? (C) 140? (D) 40?或140?
D
2.已知:如图,AB=AC=AD, ∠BAC=40?,
则∠BDC的度数为( )
(A)40? (B)30?
(C)20? (D)不能确定
C
15°或 75 °
4.如图,⊙O1、⊙O2相交于A、B两点,
直线O1O2交两圆于C、D∠O1AO2=40°,
则∠CBD等于( )
(A)110° (B)120°
(C)130° (D)140°
A
1.如图,已知圆心角∠BOC=100°,
则圆周角∠BAC的度数为( )
A、100° B、130°
C、50° D、80°
2.圆内接正三角形的一条边所对的圆周角为( )
A、30° B、60°
C、30°或150° D、60°或120°
3.如图,A、B、C三点在⊙O上,
∠AOC=100°,则∠ABC等于( )
A、140° B、110°
C、120° D、130°
C
D
D
4.若圆的一条弦把圆分成度数的比为1∶3的两条弧,
则劣弧所对的圆周角的度数为( )
A、45° B、90° C、135° D、270°
5.已知:如图,△ABC内接于
⊙O,AD是⊙O的直径,∠ABC
=30°,则∠CAD等于_________。
6. 在⊙O中,一条弦的长度等
于半径,则它所对的圆周角的
度数为_________。
7.半径为1的圆中有一条弦,如果
它的长为
那么这条弦所对的圆
A
周角的度数等于 .
60°
60°或120 °
30°或150 °
弦AB分圆为l∶5两部分,则弦AB所对
的圆周角度数等于
9. 已知:如图,AB 为⊙O的直径,∠BED=35?,
则∠ACD= ? 。
10.圆内接四边形相邻三个内角之比是3:1:6,
则这个四边形的最大角的度数为 。
30°或150 °
55
160 °
7 学以致用 作业适量 分层要求
A层(基础题)
⑶如图9,已知AB=AC=2cm, ∠BDC=60,则△ABC 的周长是 。
⑷如图10:∠A是⊙O的圆周角,∠A=40°,求∠OBC 的度数。
7 学以致用 作业适量 分层要求
B层(中等题)
⑴ 在⊙O中,∠BOC=100o,则弦BC所对的圆周角
是 度。
⑵如图11,AD是⊙O直径,BC=CD,∠A=30°,
求∠B的度数。
7 学以致用 作业适量 分层要求
C层(提高题)
如图12,AB是⊙O直径,点C在圆上,∠BAC的平分线交圆于点E,OE交BC于点H,已知AC=6,AB=10,求HE的长。
7 学以致用 作业适量 分层要求
D层(课外延拓、承上启下)
如图13:“世界杯”赛场上李铁、邵佳一、郝海东三名队员互相配合向对方球门进攻,当李带球冲到如图C点时,邵、郝也分别跟随冲到图中的D点、E点,李应把球传给谁好?请你从数学角度帮忙合情说理、分析说明。
球门
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
2、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
⌒
⌒
4、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_ _;
20°
25°
3、若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于多少度。
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
四边形与圆的位置关系
如果四边形的四个顶点在一个圆上,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.
我们可以证明圆内接四边的两个重要性质:
1.圆内接四边形对角互补.
2.圆内接四边形对的一个外角等于它的内对角.
