19.2.2一次函数的图像与性质课件(共20张PPT)
文档属性
| 名称 | 19.2.2一次函数的图像与性质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-28 00:00:00 | ||
图片预览


文档简介
课件20张PPT。14.2.2(2)
一次函数的图像与性质(一)、知识回顾:1、概念:
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
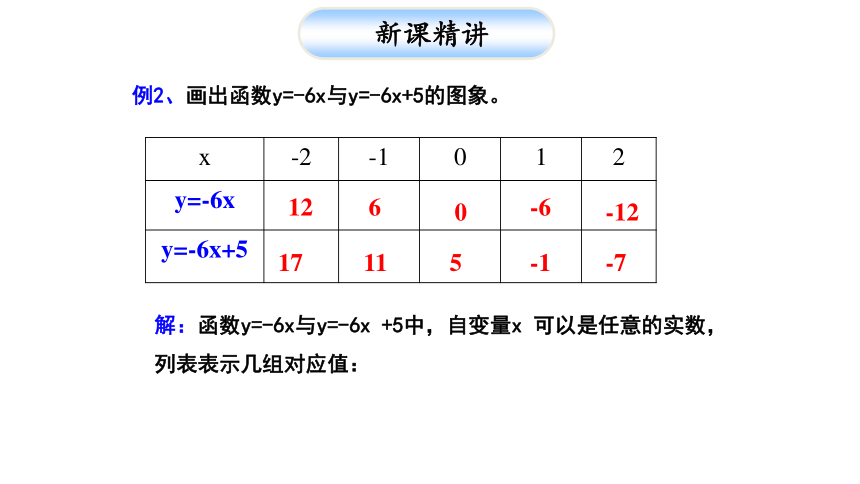
2、一次函数与正比例函数的区别与联系60-6-121217115-1-7例2、画出函数y=-6x与y=-6x+5的图象。解:函数y=-6x与y=-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:17115-7y=-6xy=-6x+5两个函数图象有什么关系?0Xy比较上面两个函数的图象的相同点和不同点。填出你的观察结果:
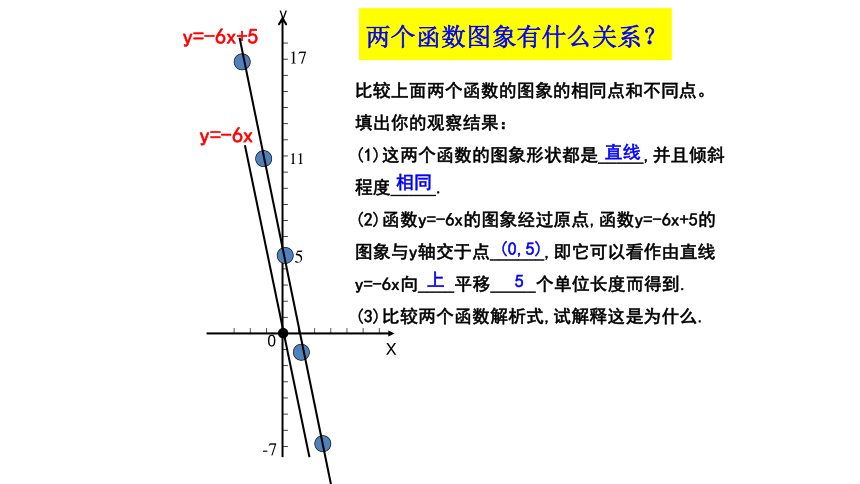
(1)这两个函数的图象形状都是_____,并且倾斜程度_____.
(2)函数y=-6x的图象经过原点,函数y=-6x+5的图象与y轴交于点______,即它可以看作由直线y=-6x向____平移_____个单位长度而得到.
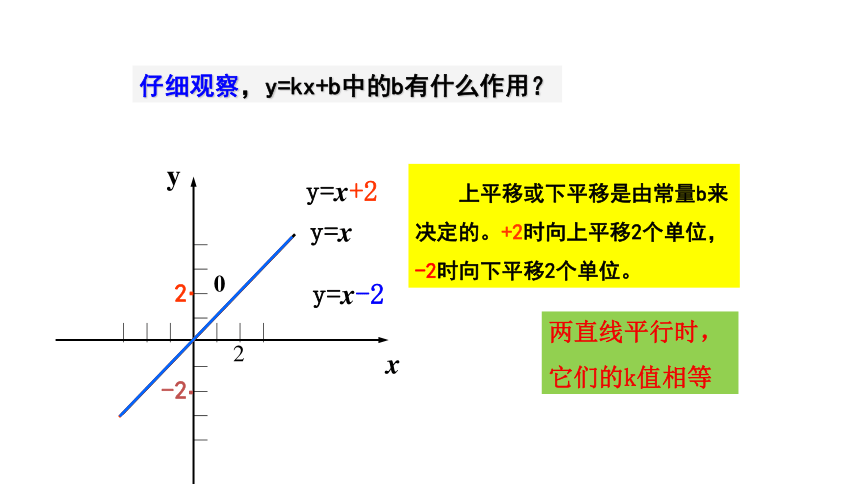
(3)比较两个函数解析式,试解释这是为什么.直线(0,5)上5相同y=xy=x+2y=x-2y20仔细观察,y=kx+b中的b有什么作用?-2.. 上平移或下平移是由常量b来决定的。+2时向上平移2个单位,-2时向下平移2个单位。两直线平行时,
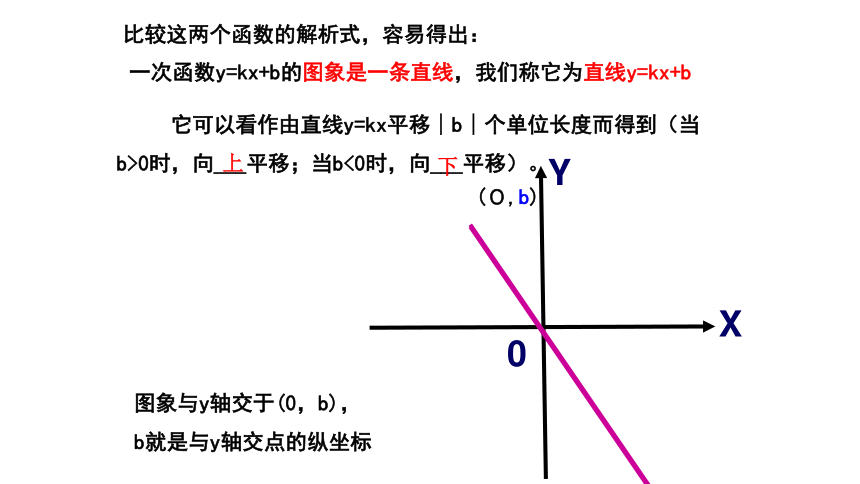
它们的k值相等比较这两个函数的解析式,容易得出:一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b 它可以看作由直线y=kx平移∣b∣个单位长度而得到(当b>0时,向___平移;当b<0时,向___平移)。下上(0,b)图象与y轴交于(0,b),
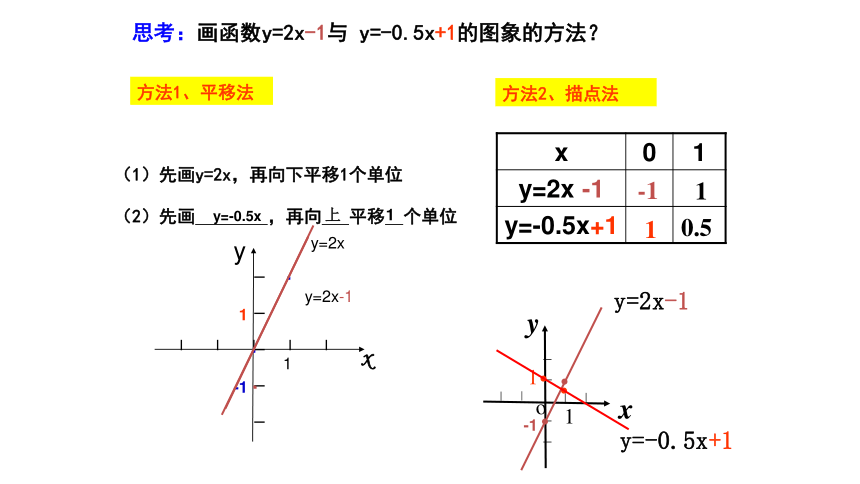
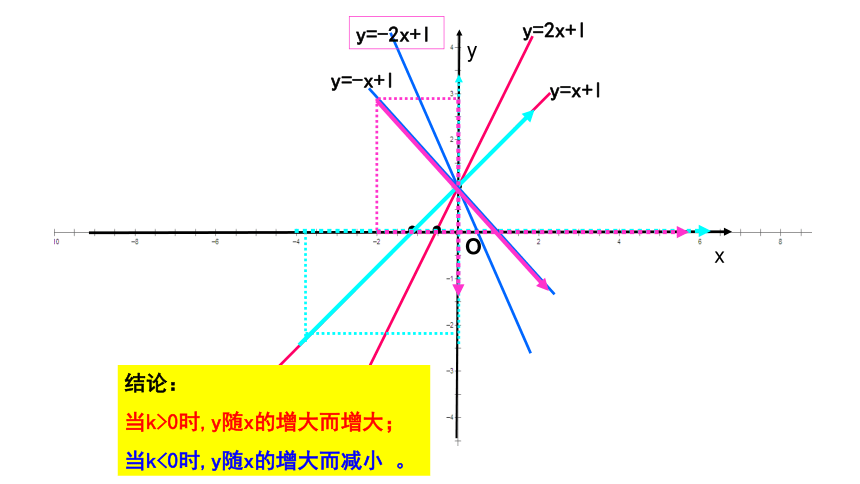
b就是与y轴交点的纵坐标思考:画函数y=2x-1与 y=-0.5x+1的图象的方法?yxo11····y=2x-1 y=-0.5x+1 -1110.5方法1、平移法方法2、描点法(1)先画y=2x,再向下平移1个单位(2)先画 ,再向 平移 个单位I I I I II I I I I1-1...y=2xy=2x-11xy-1y=-0.5x上1y=x+ly=2x+l●●●Oyxy=-x+ly=-2x+l结论:
当k>0时,y随x的增大而增大;
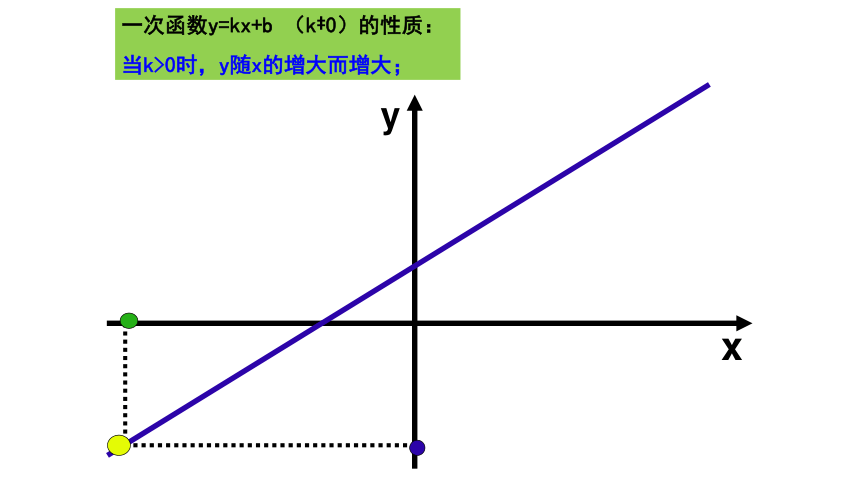
当k<0时,y随x的增大而减小 。一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大; yxyx一次函数y=kx+b (k?0)的性质:
当k<0时,y随x的增大而减小. 概括:一次函数y=kx+b k决定直线的倾斜方向1、当k>0时,y随x的增大而增大2、当k<0时,y随x的增大而减小3、当 k 相等时,直线平行4、当 |k| 越大时,图象越靠近y轴 b 决定直线与y轴交点位置1、当b>0时,直线交于y正半轴4、当b相等时,直线交于y轴上同一点2、当b<0时,直线交于y负半轴3、当b = 0时,直线交于坐标原点概括:一次函数y=kx+b一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0大大不过四大小不过二例1、已知:一次函数 y=(5m-3)x+(2-n).
(1)当 m 为何值时,y 随 x 的增大而减小;
(2)当 m、n 分别为何值时,一次函数与 y 轴的交点在 x 轴的上方?3、体验数形结合的思想与方法,从特殊到一般的思想与方法.1、画一次函数的图象:平移法、描点法。2、一次函数的图象与性质,常数k、b的意义和作用.小 结解:(1)题意知:2m+4>0,已知直线y=(2m+4)x+m-3,求:
(1)当m为何值时,y随x的增大而增大?
(2)当m为何值时,图象与y轴的交点在x轴下方?
(3)当m为何值时,函数图象经过原点?
(4)当m为何值时,这条直线平行直线y=-x?∴m>-2.(2)题意知:m-3<0且2m+4≠0,∴m<3且m≠-2.(3)题意知:m-3=0∴m=3.(4)题意知:2m+4=-1,【合作探究】1.在同一直角坐标系内,直线y=-2x与y=-2x+3的位置关系为_ ___.
2.如图所示,是一次函数y=kx+b的图象,则( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
3.已知一次函数y=(m-2)x+m-3.
(1)若函数图象上有两点A(x1,y1),B(x2,y2)
当x1>x2时,y1<y2,求m的范围.
(2)若函数图象不经过第二象限,求m的取值范围.互相平行解: (1)由题意知y随x增大而减小,∴m-2<0, ∴m<2;(2)分两种情况:
①当图象只过一、三象限时,B∴m=3.综合①、②得:2<m≤3时,函数图象不过第二象限.m-2>0,
m-3=0,②当图象过一、三、四象限时,∴20,
m-3<0,1、书面作业:课本第99页 第5题;k<0一、二、三C一、二、四1.2.3.如下图是函数 y = 的图象,
请说说这个函数的最小值是多少,并说明理由.31xyO12234
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
2、一次函数与正比例函数的区别与联系60-6-121217115-1-7例2、画出函数y=-6x与y=-6x+5的图象。解:函数y=-6x与y=-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:17115-7y=-6xy=-6x+5两个函数图象有什么关系?0Xy比较上面两个函数的图象的相同点和不同点。填出你的观察结果:
(1)这两个函数的图象形状都是_____,并且倾斜程度_____.
(2)函数y=-6x的图象经过原点,函数y=-6x+5的图象与y轴交于点______,即它可以看作由直线y=-6x向____平移_____个单位长度而得到.
(3)比较两个函数解析式,试解释这是为什么.直线(0,5)上5相同y=xy=x+2y=x-2y20仔细观察,y=kx+b中的b有什么作用?-2.. 上平移或下平移是由常量b来决定的。+2时向上平移2个单位,-2时向下平移2个单位。两直线平行时,
它们的k值相等比较这两个函数的解析式,容易得出:一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b 它可以看作由直线y=kx平移∣b∣个单位长度而得到(当b>0时,向___平移;当b<0时,向___平移)。下上(0,b)图象与y轴交于(0,b),
b就是与y轴交点的纵坐标思考:画函数y=2x-1与 y=-0.5x+1的图象的方法?yxo11····y=2x-1 y=-0.5x+1 -1110.5方法1、平移法方法2、描点法(1)先画y=2x,再向下平移1个单位(2)先画 ,再向 平移 个单位I I I I II I I I I1-1...y=2xy=2x-11xy-1y=-0.5x上1y=x+ly=2x+l●●●Oyxy=-x+ly=-2x+l结论:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小 。一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大; yxyx一次函数y=kx+b (k?0)的性质:
当k<0时,y随x的增大而减小. 概括:一次函数y=kx+b k决定直线的倾斜方向1、当k>0时,y随x的增大而增大2、当k<0时,y随x的增大而减小3、当 k 相等时,直线平行4、当 |k| 越大时,图象越靠近y轴 b 决定直线与y轴交点位置1、当b>0时,直线交于y正半轴4、当b相等时,直线交于y轴上同一点2、当b<0时,直线交于y负半轴3、当b = 0时,直线交于坐标原点概括:一次函数y=kx+b一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0大大不过四大小不过二例1、已知:一次函数 y=(5m-3)x+(2-n).
(1)当 m 为何值时,y 随 x 的增大而减小;
(2)当 m、n 分别为何值时,一次函数与 y 轴的交点在 x 轴的上方?3、体验数形结合的思想与方法,从特殊到一般的思想与方法.1、画一次函数的图象:平移法、描点法。2、一次函数的图象与性质,常数k、b的意义和作用.小 结解:(1)题意知:2m+4>0,已知直线y=(2m+4)x+m-3,求:
(1)当m为何值时,y随x的增大而增大?
(2)当m为何值时,图象与y轴的交点在x轴下方?
(3)当m为何值时,函数图象经过原点?
(4)当m为何值时,这条直线平行直线y=-x?∴m>-2.(2)题意知:m-3<0且2m+4≠0,∴m<3且m≠-2.(3)题意知:m-3=0∴m=3.(4)题意知:2m+4=-1,【合作探究】1.在同一直角坐标系内,直线y=-2x与y=-2x+3的位置关系为_ ___.
2.如图所示,是一次函数y=kx+b的图象,则( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
3.已知一次函数y=(m-2)x+m-3.
(1)若函数图象上有两点A(x1,y1),B(x2,y2)
当x1>x2时,y1<y2,求m的范围.
(2)若函数图象不经过第二象限,求m的取值范围.互相平行解: (1)由题意知y随x增大而减小,∴m-2<0, ∴m<2;(2)分两种情况:
①当图象只过一、三象限时,B∴m=3.综合①、②得:2<m≤3时,函数图象不过第二象限.m-2>0,
m-3=0,②当图象过一、三、四象限时,∴2
m-3<0,1、书面作业:课本第99页 第5题;k<0一、二、三C一、二、四1.2.3.如下图是函数 y = 的图象,
请说说这个函数的最小值是多少,并说明理由.31xyO12234
