新人教版高中数学必修三2.1.1《简单随机抽样》(23张PPT)
文档属性
| 名称 | 新人教版高中数学必修三2.1.1《简单随机抽样》(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 680.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-29 00:00:00 | ||
图片预览







文档简介
数理统计所要解决的问题是如何根据样本来推断总体,用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。第一个问题:总体、个体、样本、样本容量的概念.
总体:所要考察对象的全体。
个体:总体中的每一个考察对象。
样本:从总体中抽取的一部分个体叫做这个总体的一个样本。
样本容量:样本中个体的数目。
在1936年美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意测验,调查兰顿 和罗斯福中谁将当选下一届总统。为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(在1936年电话和汽车只有少数富人拥有),通过分析收回的调查表,显示兰顿非常受欢迎。于是此杂志预测兰顿将在选举中获胜。 实际选举结果正好相反,最后罗斯福在选举中获胜。其数据如下:
候选人 预测结果 (%) 选举结果 (%)
Landon 57 38
Roosevelt 43 62
一般地,设一个总体中含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就称这样的抽样为简单随机抽样。
注意以下四点:
(1)它要求总体中的个体数有限;
(3)它是一种不放回抽样;
(4)总体中每一个个体被抽取的机会相等。
(2)它是从总体中逐个进行抽取;
简单随机抽样的概念:
有限性
逐个性
不放回性
机会均等性
下列抽取样本的方式是简单随机抽样吗?为什么?
(1)从无限多个个体中抽取用50个个体作为样本。
(3)箱子里有100枝铅笔,现从中选取10枝进行检验,在抽样操作时,从中任意拿出一枝检测后再放回箱子里。
(2)从50个个体中一次性抽取5个个体作为样本。
(4)从个体数为N的总体中抽取一个容量为n的样本,
每个个体被抽到的机会不相等。
(1)编号制签(从0到N-1或1到N编号)
1.简单随机抽样方法——抽签法(抓阄法)
(2)搅拌均匀
(3)逐个不放回抽取n次
步骤:
例如:我们班有44名学生,现从中抽出5名学生去参加学生座谈会,要使每名学生的机会均等,我们应该怎么做?
1.抽签法(抓阄法)
2.随机数表法
简单随机抽样
优点:
简单易行,当总体的个数不多时,抽签法能够保证每个个体被抽中的机会都相等
缺点:
1)当总体的个数非常大时,制作号签费时费力;
2)号签很多时较难搅拌均匀,难以保证每个个体入选的可能性相等,从而造成代表性差。
1.简单随机抽样方法——抽签法(抓阄法)
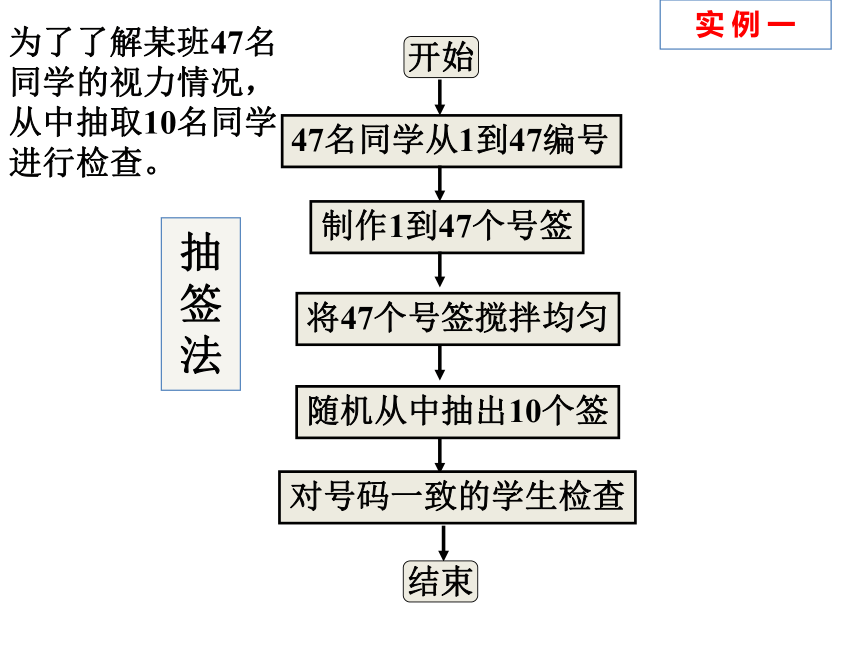
开始
47名同学从1到47编号
制作1到47个号签
将47个号签搅拌均匀
随机从中抽出10个签
对号码一致的学生检查
结束
为了了解某班47名
同学的视力情况,
从中抽取10名同学
进行检查。
抽签法
实 例 一
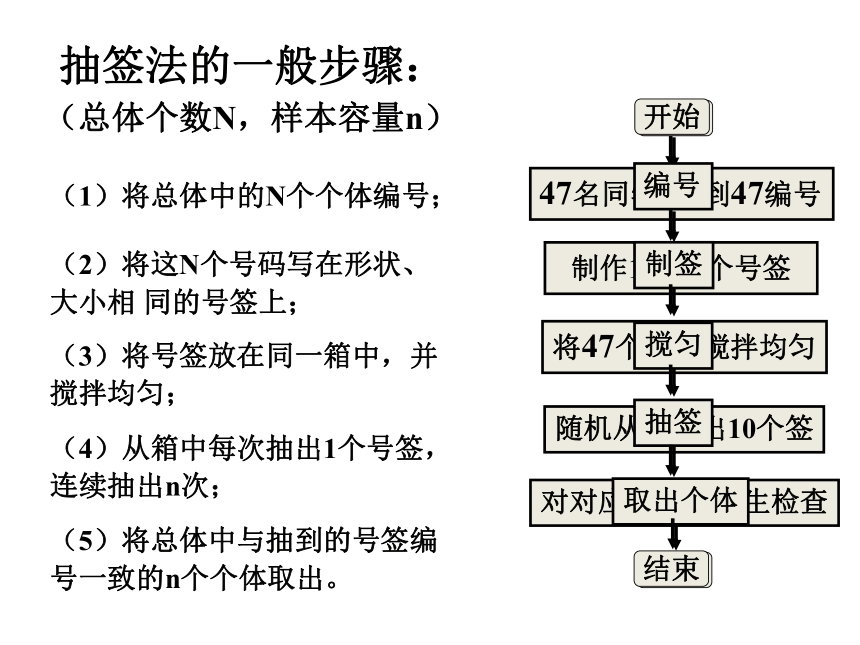
抽签法的一般步骤:
(1)将总体中的N个个体编号;
(2)将这N个号码写在形状、大小相 同的号签上;
(3)将号签放在同一箱中,并搅拌均匀;
(4)从箱中每次抽出1个号签,连续抽出n次;
(5)将总体中与抽到的号签编号一致的n个个体取出。
(总体个数N,样本容量n)
开始
编号
制签
搅匀
抽签
取出个体
结束
2.简单随机抽样方法——随机数表法
随机数表是统计工作者用计算机生成的随机数,由数字0~9组成,并保证表中的每个位置上的数字出现的机会都是一样的。
步骤(1)将总体的个体编号(如:总体容量是两
位数,从00~(N-1);三位数,从000~(N-1). 依此类推 )
(2)在随机数表中选择一个开始数字(任选)
(3)确定读数方向获取样本号码(上、下、左、右任选其一)
注意事项:
(1)“两不要”(超出编号范围的不要,重复的不要)
(2)个体编号时,根据总体容量选择适当编号;
(3)读数(可以向右、向左、向上、向下)
随机数表
教材103页
例:要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验。
1、将800袋牛奶编号,000,001,…,799
2、在随机数表(课本103页)中任选一数,例如第8行第7列,是7。
3、从7开始往右读(方向随意),得到第一个三位数785<编号799,将对应编号的牛奶取出;继续向右读,得到916>编号799,舍弃;如此继续下去,直至抽出60袋牛奶。
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
6行:
7行:
8行:
9行:
10行:
第三步,从选定的数7开始向右读(读数的方向也可以是向左、向上、向下等),得到一个三位数785,由于785<799,说明号码785在总体内,将它取出;继续向右读,得到916,由于916>799,将它去掉,按照这种方法继续向右读,又取出567,199,507,…,依次下去,直到样本的60个号码全部取出,这样我们就得到一个容量为60的样本。
利用随机数表法从含有N个个体的总体中抽取一个容量为n的样本,其抽样步骤如何?
第一步,将总体中的所有个体编号.
第二步,在随机数表中任选一个数作为起始数.
第三步,从选定的数开始依次向右(向左、向上、向下)读,将编号范围内的数取出,编号范围外的数去掉,直到取满n个号码为止,就得到一个容量为n的样本.
练习1.下列抽取样本的方式是属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本;
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后,再把它放回盒子里;
③从8台电脑中不放回的随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.① B.② C.③ D.以上都不对
C
2.对于简单随机抽样,个体被抽到的机会( )
A.相等 B.不相等
C.不确定 D.与抽取的次数有关
答案: A
3. 抽签法中确保样本代表性的关键是( )
A.制签 B.搅拌均匀
C.逐一抽取 D.抽取不放回
答案:B
4.为了了解全校240名高一学生的身高情况,从中抽取40名学生进行测量.下列说法正确的是( )
A.总体是240名 B.个体是每一个学生
C.样本是40名学生 D.样本容量是40
答案:D
5.从10个篮球中任取一个,检验其质量,则抽样为( )
A.简单随机抽样 B.不放回或放回抽样
C.随机数表法 D.有放回抽样
答案:A
6.简单随机抽样的结果 ( )
A.完全由抽样方式所决定
B.完全由随机性来决定
C.完全由人为因素所决定
D.完全由计算方法所决定
答案:B
7.为了了解某县中考学生数学成绩的情况,从中抽取20本密封试卷,每本30份试卷,这个问题中的样本容量是( )
A.20 B.30 C.60 D.600
答案:D
8.从参加计算机水平测试的5000名学生的成绩中抽取200名学生的成绩进行分析,在这个问题中,200名学生成绩的全体是( )
A.总体 B.个体
C.从总体中抽取的一个样本 D.总体的容量
答案:C
9. 从某年级500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是( )
A.500名学生是总体
B.每个被抽查的学生是样本
C.抽取的60名学生的体重是一个样本
D.抽取的60名学生的体重是样本总量
答案:C
10.某校高一共有10个班,编号1至10,某项调查要从中抽取三个班作为样本,现用抽签法抽取样本,每次抽取一个号码,共抽3次,设五班第一次被抽到的可能性为a,第二次被抽到的可能性为b,则( )
D
总体:所要考察对象的全体。
个体:总体中的每一个考察对象。
样本:从总体中抽取的一部分个体叫做这个总体的一个样本。
样本容量:样本中个体的数目。
在1936年美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意测验,调查兰顿 和罗斯福中谁将当选下一届总统。为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(在1936年电话和汽车只有少数富人拥有),通过分析收回的调查表,显示兰顿非常受欢迎。于是此杂志预测兰顿将在选举中获胜。 实际选举结果正好相反,最后罗斯福在选举中获胜。其数据如下:
候选人 预测结果 (%) 选举结果 (%)
Landon 57 38
Roosevelt 43 62
一般地,设一个总体中含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就称这样的抽样为简单随机抽样。
注意以下四点:
(1)它要求总体中的个体数有限;
(3)它是一种不放回抽样;
(4)总体中每一个个体被抽取的机会相等。
(2)它是从总体中逐个进行抽取;
简单随机抽样的概念:
有限性
逐个性
不放回性
机会均等性
下列抽取样本的方式是简单随机抽样吗?为什么?
(1)从无限多个个体中抽取用50个个体作为样本。
(3)箱子里有100枝铅笔,现从中选取10枝进行检验,在抽样操作时,从中任意拿出一枝检测后再放回箱子里。
(2)从50个个体中一次性抽取5个个体作为样本。
(4)从个体数为N的总体中抽取一个容量为n的样本,
每个个体被抽到的机会不相等。
(1)编号制签(从0到N-1或1到N编号)
1.简单随机抽样方法——抽签法(抓阄法)
(2)搅拌均匀
(3)逐个不放回抽取n次
步骤:
例如:我们班有44名学生,现从中抽出5名学生去参加学生座谈会,要使每名学生的机会均等,我们应该怎么做?
1.抽签法(抓阄法)
2.随机数表法
简单随机抽样
优点:
简单易行,当总体的个数不多时,抽签法能够保证每个个体被抽中的机会都相等
缺点:
1)当总体的个数非常大时,制作号签费时费力;
2)号签很多时较难搅拌均匀,难以保证每个个体入选的可能性相等,从而造成代表性差。
1.简单随机抽样方法——抽签法(抓阄法)
开始
47名同学从1到47编号
制作1到47个号签
将47个号签搅拌均匀
随机从中抽出10个签
对号码一致的学生检查
结束
为了了解某班47名
同学的视力情况,
从中抽取10名同学
进行检查。
抽签法
实 例 一
抽签法的一般步骤:
(1)将总体中的N个个体编号;
(2)将这N个号码写在形状、大小相 同的号签上;
(3)将号签放在同一箱中,并搅拌均匀;
(4)从箱中每次抽出1个号签,连续抽出n次;
(5)将总体中与抽到的号签编号一致的n个个体取出。
(总体个数N,样本容量n)
开始
编号
制签
搅匀
抽签
取出个体
结束
2.简单随机抽样方法——随机数表法
随机数表是统计工作者用计算机生成的随机数,由数字0~9组成,并保证表中的每个位置上的数字出现的机会都是一样的。
步骤(1)将总体的个体编号(如:总体容量是两
位数,从00~(N-1);三位数,从000~(N-1). 依此类推 )
(2)在随机数表中选择一个开始数字(任选)
(3)确定读数方向获取样本号码(上、下、左、右任选其一)
注意事项:
(1)“两不要”(超出编号范围的不要,重复的不要)
(2)个体编号时,根据总体容量选择适当编号;
(3)读数(可以向右、向左、向上、向下)
随机数表
教材103页
例:要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验。
1、将800袋牛奶编号,000,001,…,799
2、在随机数表(课本103页)中任选一数,例如第8行第7列,是7。
3、从7开始往右读(方向随意),得到第一个三位数785<编号799,将对应编号的牛奶取出;继续向右读,得到916>编号799,舍弃;如此继续下去,直至抽出60袋牛奶。
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
6行:
7行:
8行:
9行:
10行:
第三步,从选定的数7开始向右读(读数的方向也可以是向左、向上、向下等),得到一个三位数785,由于785<799,说明号码785在总体内,将它取出;继续向右读,得到916,由于916>799,将它去掉,按照这种方法继续向右读,又取出567,199,507,…,依次下去,直到样本的60个号码全部取出,这样我们就得到一个容量为60的样本。
利用随机数表法从含有N个个体的总体中抽取一个容量为n的样本,其抽样步骤如何?
第一步,将总体中的所有个体编号.
第二步,在随机数表中任选一个数作为起始数.
第三步,从选定的数开始依次向右(向左、向上、向下)读,将编号范围内的数取出,编号范围外的数去掉,直到取满n个号码为止,就得到一个容量为n的样本.
练习1.下列抽取样本的方式是属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本;
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后,再把它放回盒子里;
③从8台电脑中不放回的随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.① B.② C.③ D.以上都不对
C
2.对于简单随机抽样,个体被抽到的机会( )
A.相等 B.不相等
C.不确定 D.与抽取的次数有关
答案: A
3. 抽签法中确保样本代表性的关键是( )
A.制签 B.搅拌均匀
C.逐一抽取 D.抽取不放回
答案:B
4.为了了解全校240名高一学生的身高情况,从中抽取40名学生进行测量.下列说法正确的是( )
A.总体是240名 B.个体是每一个学生
C.样本是40名学生 D.样本容量是40
答案:D
5.从10个篮球中任取一个,检验其质量,则抽样为( )
A.简单随机抽样 B.不放回或放回抽样
C.随机数表法 D.有放回抽样
答案:A
6.简单随机抽样的结果 ( )
A.完全由抽样方式所决定
B.完全由随机性来决定
C.完全由人为因素所决定
D.完全由计算方法所决定
答案:B
7.为了了解某县中考学生数学成绩的情况,从中抽取20本密封试卷,每本30份试卷,这个问题中的样本容量是( )
A.20 B.30 C.60 D.600
答案:D
8.从参加计算机水平测试的5000名学生的成绩中抽取200名学生的成绩进行分析,在这个问题中,200名学生成绩的全体是( )
A.总体 B.个体
C.从总体中抽取的一个样本 D.总体的容量
答案:C
9. 从某年级500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是( )
A.500名学生是总体
B.每个被抽查的学生是样本
C.抽取的60名学生的体重是一个样本
D.抽取的60名学生的体重是样本总量
答案:C
10.某校高一共有10个班,编号1至10,某项调查要从中抽取三个班作为样本,现用抽签法抽取样本,每次抽取一个号码,共抽3次,设五班第一次被抽到的可能性为a,第二次被抽到的可能性为b,则( )
D
