北师大版必修一第二章2.3.1 函数的单调性(1)课件(共22张)
文档属性
| 名称 | 北师大版必修一第二章2.3.1 函数的单调性(1)课件(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-30 00:00:00 | ||
图片预览






文档简介
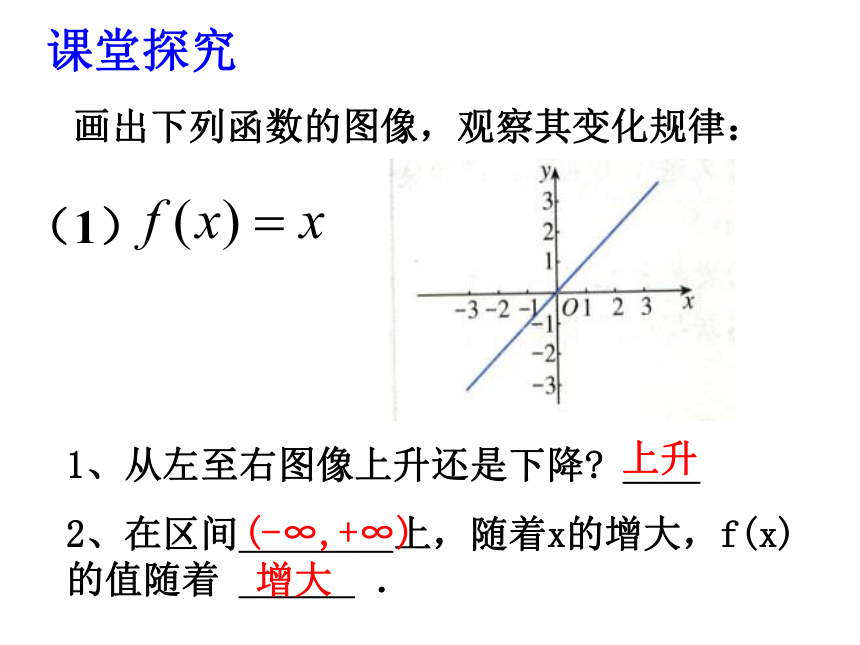
课件22张PPT。§2.3.1函数的单调性(1) 建立函数的目的是研究函数值与自变量的关系,自变量的变化对函数值变化的影响是经常受到关注的问题.例如水位的涨落随时间变化的规律,是防涝抗旱工作中必须解决的实际问题.下面我们开始研究函数在这方面的一个主要性质——函数的单调性.画出下列函数的图像,观察其变化规律: 1、从左至右图像上升还是下降? ____
2、在区间________上,随着x的增大,f(x)的值随着 ______ .(1)(-∞,+∞)增大上升课堂探究1.在区间______上,f(x)的值随着x的增大而______.
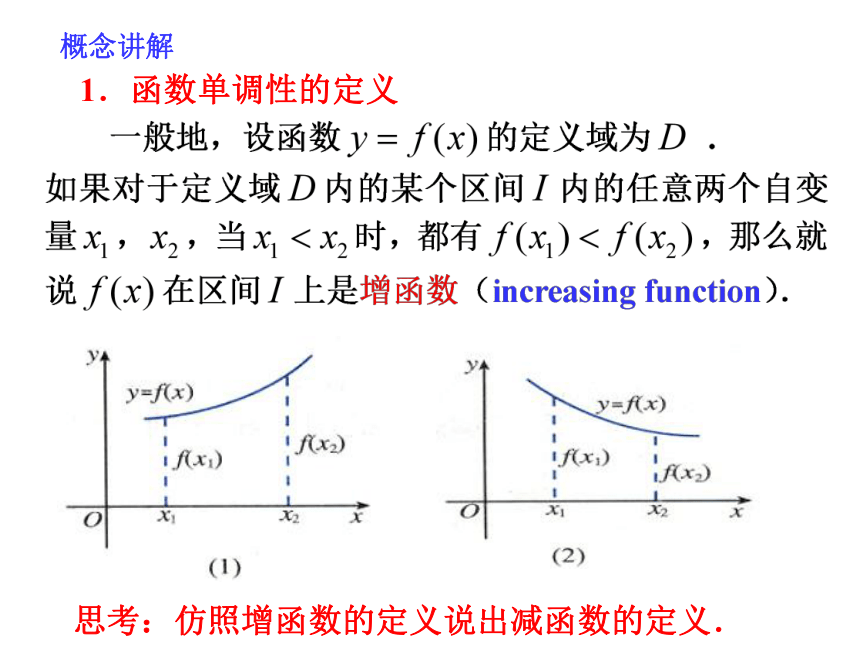
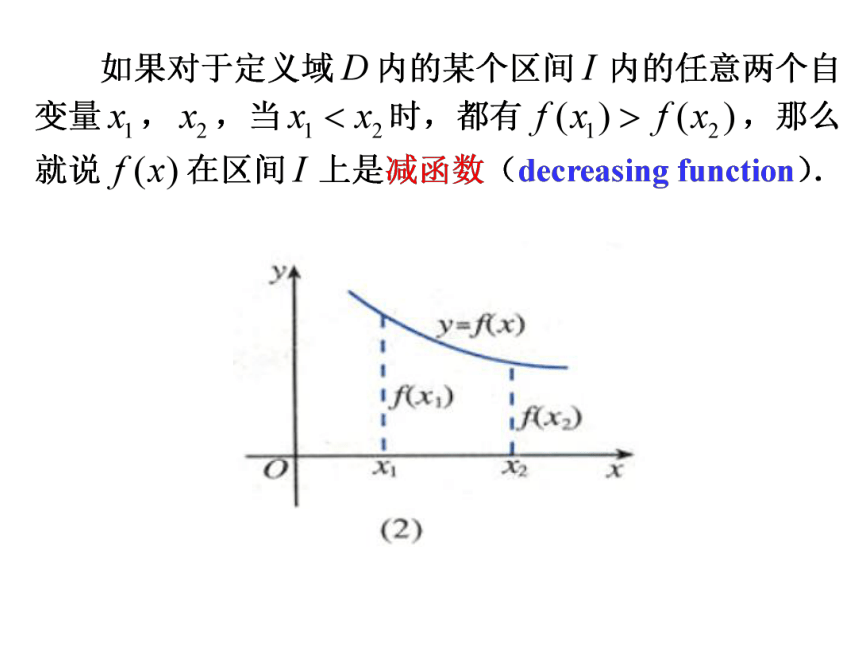
2.在区间________上,f(x)的值随着x的增大而_____. (2)(-∞,0](0,+∞)增大减小画出下列函数的图像,观察其变化规律: 概念讲解思考:仿照增函数的定义说出减函数的定义. 1.函数单调性的定义函数单调性定义的等价形式2.单调区间,单调性,单调函数 (1)如果y=f(x)在区间I 上是递增的或是递减的,那么称I 为函数y=f(x)的单调区间. (2)如果y=f(x)在定义域的某个区间I上是递增的或是递减的,那么就称函数y=f(x)在这个区间I上具有单调性. (3)如果y=f(x)在整个定义域D内是递增的或是递减的,我们分别称这个函数y=f(x)为增函数或减函数,统称为单调函数. (1)函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;注意: (2)必须是对于区间I内的任意两个自变量x1,x2;当x1f(x2),分别是增函数和减函数.(3)函数的单调区间是其定义域的子集; (4)一般地,函数f(x)在区间A、B上都是增(减)函数,并不能说函数f(x)在A∪B上是增(减)函数. 注意:函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题;对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以;例2 证明函数 在R上是增函数.证明:在R上是增函数. 1.任取 x1,x2∈I,且x12.作差 f(x1)-f(x2);
3.变形(通常是因式分解和配方);
4.定号(即判断差f(x1)-f(x2)的正负);
5.结论(即指出函数f(x)在给定的区间I上的单调性). 利用定义证明(判断)函数f(x)在给定的区间I上的单调性的一般步骤:推广:一次函数的单调性结论: 例3 说出函数 的单调区间,并指明在该区间上的单调性. 解:(-∞,0)和(0,+∞)都是函数的单调区间,在
这两个区间上函数 是减小的.证明: 设x1,x2是(0,+∞)上任意两个实数,且x1任 取→ 作 差 → 变 形 → 定 号 → 下结论
2、直接利用初等函数的单调区间。 课堂小结P40习题 A组 T3(2)(4),
T4, T5. 课外作业
2、在区间________上,随着x的增大,f(x)的值随着 ______ .(1)(-∞,+∞)增大上升课堂探究1.在区间______上,f(x)的值随着x的增大而______.
2.在区间________上,f(x)的值随着x的增大而_____. (2)(-∞,0](0,+∞)增大减小画出下列函数的图像,观察其变化规律: 概念讲解思考:仿照增函数的定义说出减函数的定义. 1.函数单调性的定义函数单调性定义的等价形式2.单调区间,单调性,单调函数 (1)如果y=f(x)在区间I 上是递增的或是递减的,那么称I 为函数y=f(x)的单调区间. (2)如果y=f(x)在定义域的某个区间I上是递增的或是递减的,那么就称函数y=f(x)在这个区间I上具有单调性. (3)如果y=f(x)在整个定义域D内是递增的或是递减的,我们分别称这个函数y=f(x)为增函数或减函数,统称为单调函数. (1)函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;注意: (2)必须是对于区间I内的任意两个自变量x1,x2;当x1
3.变形(通常是因式分解和配方);
4.定号(即判断差f(x1)-f(x2)的正负);
5.结论(即指出函数f(x)在给定的区间I上的单调性). 利用定义证明(判断)函数f(x)在给定的区间I上的单调性的一般步骤:推广:一次函数的单调性结论: 例3 说出函数 的单调区间,并指明在该区间上的单调性. 解:(-∞,0)和(0,+∞)都是函数的单调区间,在
这两个区间上函数 是减小的.证明: 设x1,x2是(0,+∞)上任意两个实数,且x1
2、直接利用初等函数的单调区间。 课堂小结P40习题 A组 T3(2)(4),
T4, T5. 课外作业
