五年级下册数学课件8.5应用广角七桥问题苏教版(共22张PPT)
文档属性
| 名称 | 五年级下册数学课件8.5应用广角七桥问题苏教版(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-30 10:42:22 | ||
图片预览




文档简介
课件22张PPT。一笔画
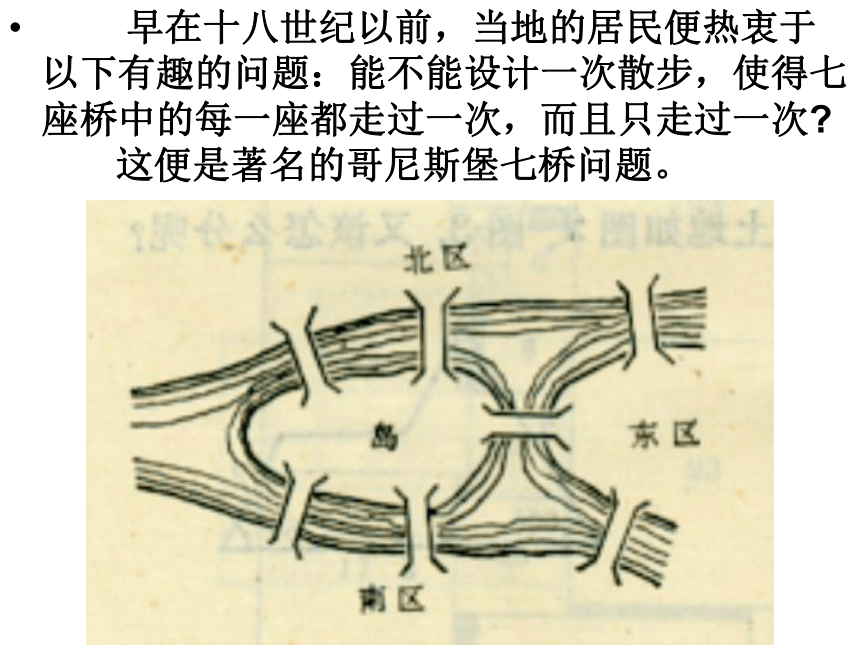
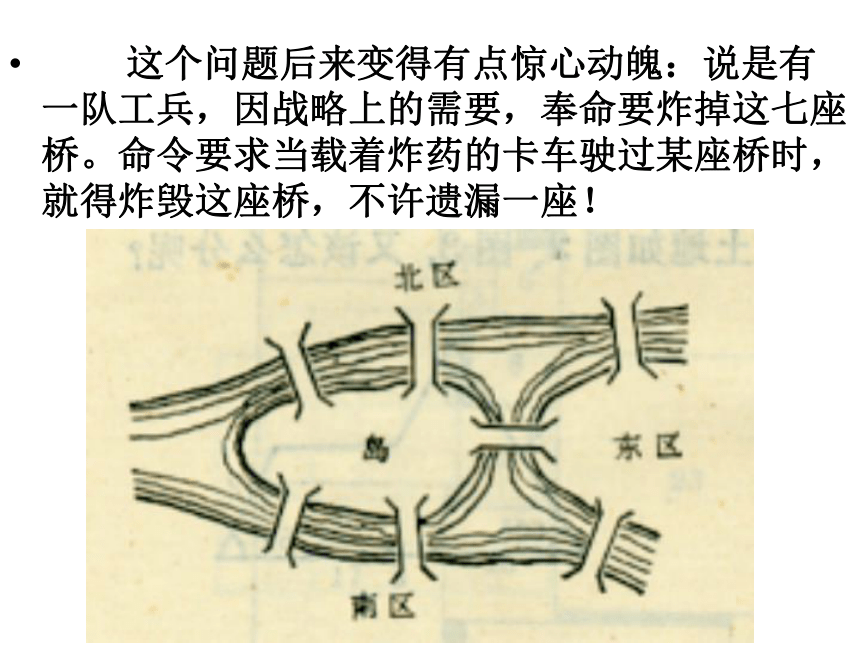
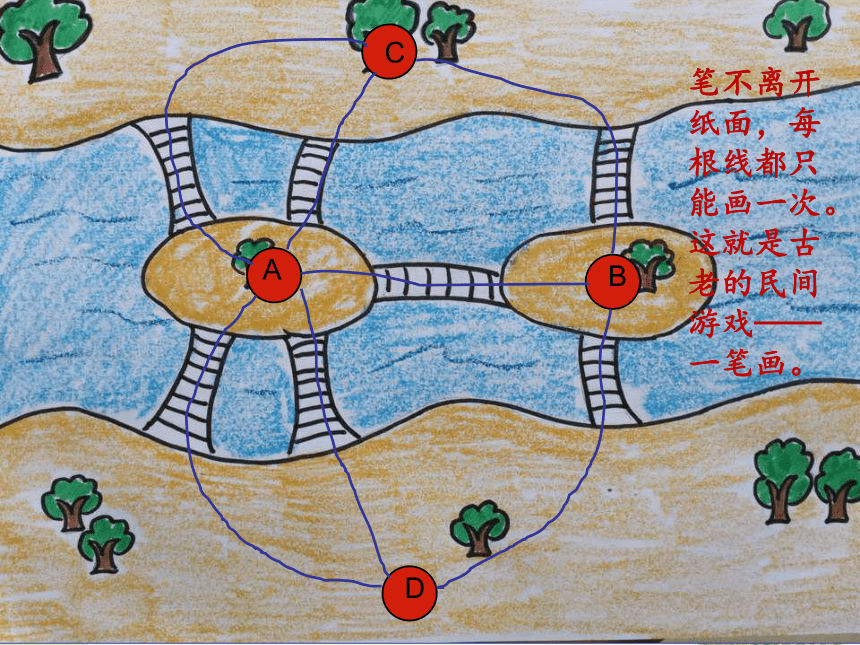
----有趣的七桥问题 著名的哥尼斯堡大学,傍倚于两条支流的河旁,使这一秀色怡人的区域,又增添了几分庄重的韵味!有七座桥横跨普累格河及其支流。这一别致的桥群,古往今来,吸引了众多的游人来此散步。 早在十八世纪以前,当地的居民便热衷于以下有趣的问题:能不能设计一次散步,使得七座桥中的每一座都走过一次,而且只走过一次? 这便是著名的哥尼斯堡七桥问题。 这个问题后来变得有点惊心动魄:说是有一队工兵,因战略上的需要,奉命要炸掉这七座桥。命令要求当载着炸药的卡车驶过某座桥时,就得炸毁这座桥,不许遗漏一座! 问题的魔力,竟然吸引了天才的欧拉(Euler。1707---1783)。这位年轻的瑞士数学家,以其独具的慧眼,看出了这个似乎是趣味几何问题的潜在意义。 笔不离开纸面,每根线都只能画一次。这就是古老的民间游戏——一笔画。
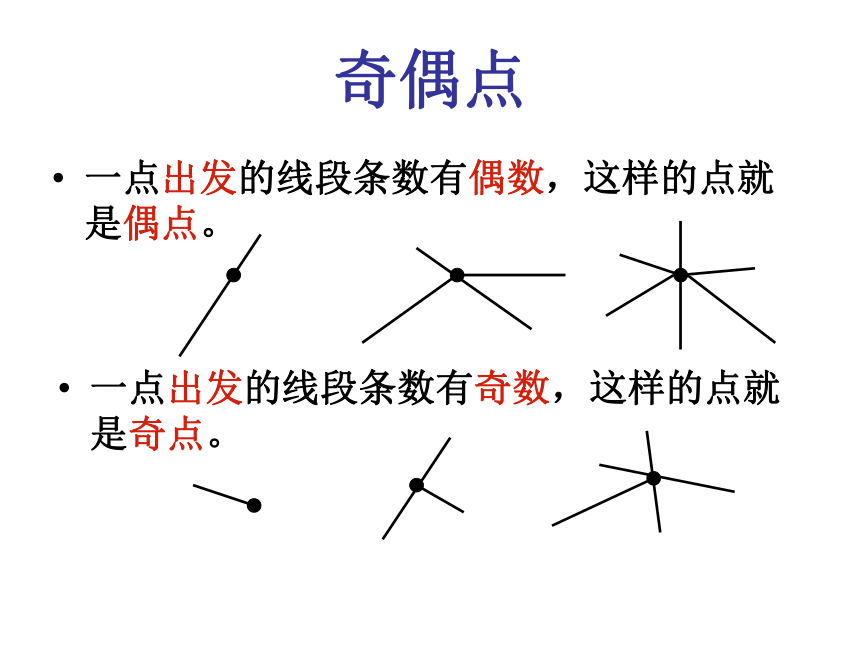
图1图2图3奇偶点一点出发的线段条数有偶数,这样的点就是偶点。一点出发的线段条数有奇数,这样的点就是奇点。图1图2图3完成操作26人一小组合作,每人画出一个能一笔画成的图形,并数数奇点、偶点的个数。组长带领组员将每个同学的姓名及所画图形中奇点、偶点的个数填在表中。完成操作2观察表中的数据,联系不能一笔画成的图形中奇点和偶点的个数进行思考,你有什么发现?和同学说说。能2个2个能2个4个能0个6个能0个10个能0个8个能0个9个1.凡能一笔画的图形必须是一个连通图;
2.凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。例如下图都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→① (连通图:通俗点就是任意两个点都有路径可以连通。)? 3.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。例如下图的线路是:①→②→③→①→④ 问题解决了,可是大家形成了每周六去散步的习惯,如果让你当一回设计师,在此基础上进行二期工程改造,再建一座桥,你能否不重复一次走完八座桥?下面的图形能一笔画成吗?( √ )( √ )( × )( × )( √ )知识应用
下列哪几个图能一笔画出?如果能,给出画法。分析点拨:
图(1)中共9个点,都是偶点,所以可以一笔画出,九个点中的任意一个都可以作为起点。
图(2)中有四个奇点,不能一笔画出。
图(3)中共有十个点,每一个点都是偶点,可以一笔画出,任选一点作为起点均可。知识应用 小明今天去逛超市,怎样走才能不重复不遗漏地逛完整个超市?例2:如果两只蚂蚁分别从甲、乙两处出发,那么,哪一只能够不重复地爬遍所有的小路?应该怎样爬?某花园小径如图,问:你能否从图中点1出发不重复地走过所有小径?如果能,请标出所经过各点的顺序;如果不能,请标出必须重复走的小径。
----有趣的七桥问题 著名的哥尼斯堡大学,傍倚于两条支流的河旁,使这一秀色怡人的区域,又增添了几分庄重的韵味!有七座桥横跨普累格河及其支流。这一别致的桥群,古往今来,吸引了众多的游人来此散步。 早在十八世纪以前,当地的居民便热衷于以下有趣的问题:能不能设计一次散步,使得七座桥中的每一座都走过一次,而且只走过一次? 这便是著名的哥尼斯堡七桥问题。 这个问题后来变得有点惊心动魄:说是有一队工兵,因战略上的需要,奉命要炸掉这七座桥。命令要求当载着炸药的卡车驶过某座桥时,就得炸毁这座桥,不许遗漏一座! 问题的魔力,竟然吸引了天才的欧拉(Euler。1707---1783)。这位年轻的瑞士数学家,以其独具的慧眼,看出了这个似乎是趣味几何问题的潜在意义。 笔不离开纸面,每根线都只能画一次。这就是古老的民间游戏——一笔画。
图1图2图3奇偶点一点出发的线段条数有偶数,这样的点就是偶点。一点出发的线段条数有奇数,这样的点就是奇点。图1图2图3完成操作26人一小组合作,每人画出一个能一笔画成的图形,并数数奇点、偶点的个数。组长带领组员将每个同学的姓名及所画图形中奇点、偶点的个数填在表中。完成操作2观察表中的数据,联系不能一笔画成的图形中奇点和偶点的个数进行思考,你有什么发现?和同学说说。能2个2个能2个4个能0个6个能0个10个能0个8个能0个9个1.凡能一笔画的图形必须是一个连通图;
2.凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。例如下图都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→① (连通图:通俗点就是任意两个点都有路径可以连通。)? 3.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。例如下图的线路是:①→②→③→①→④ 问题解决了,可是大家形成了每周六去散步的习惯,如果让你当一回设计师,在此基础上进行二期工程改造,再建一座桥,你能否不重复一次走完八座桥?下面的图形能一笔画成吗?( √ )( √ )( × )( × )( √ )知识应用
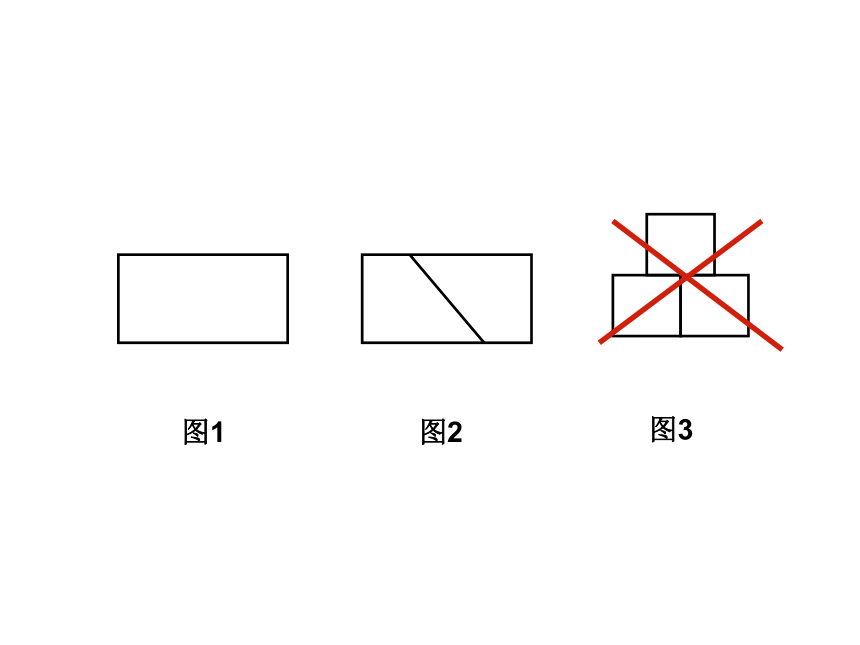
下列哪几个图能一笔画出?如果能,给出画法。分析点拨:
图(1)中共9个点,都是偶点,所以可以一笔画出,九个点中的任意一个都可以作为起点。
图(2)中有四个奇点,不能一笔画出。
图(3)中共有十个点,每一个点都是偶点,可以一笔画出,任选一点作为起点均可。知识应用 小明今天去逛超市,怎样走才能不重复不遗漏地逛完整个超市?例2:如果两只蚂蚁分别从甲、乙两处出发,那么,哪一只能够不重复地爬遍所有的小路?应该怎样爬?某花园小径如图,问:你能否从图中点1出发不重复地走过所有小径?如果能,请标出所经过各点的顺序;如果不能,请标出必须重复走的小径。
