集合中元素个数课件(26张 )
文档属性
| 名称 | 集合中元素个数课件(26张 ) |  | |
| 格式 | zip | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-02 23:59:59 | ||
图片预览








文档简介
课件26张PPT。阅读材料
集合中元素的个数例1 学校先举办了一次田径运动会,某班有8
名同学参赛,又举办了一次球类运动会。这个
班有12名同学参赛,两次运动会都参赛的有3
人。两次运动会中,这个班共有多少名同学参
赛?
分析:设A为田径运动会参赛的学生的集合,B
为球类运动会参赛的学生的集合。那么A∩B就
是两次运动会都参赛的学生的集合。
试分析 A∪B、 A、B、A∩B中元素个数的关系.解:设A={田径运动会参赛的学生},
B={球类运动会参赛的学生},那么,
A∩B={两次运动会都参赛的学生},
A∪B={参赛的学生}。
∴ card(A∪B)
= card(A)+ card(B)-card(A∩B)
=8+12-3=17。
答:两次运动会中,这个班共有17名同学参赛。
用图来求解 :例2.某班学生参加数学课外小组的人数是参加
物理课外小组的人数的2倍,同时参加两个课外
小组的人数是5人,至少参加一个课外活动小组
的人数为25人.试求参加数学小组、物理小组的
人数各是多少?参加数学小组20人,参加物理小组10人. card(A∪B)
= card(A)+ card(B)-card(A∩B)即 25=2x+x-5
x=10 card(A∪B)
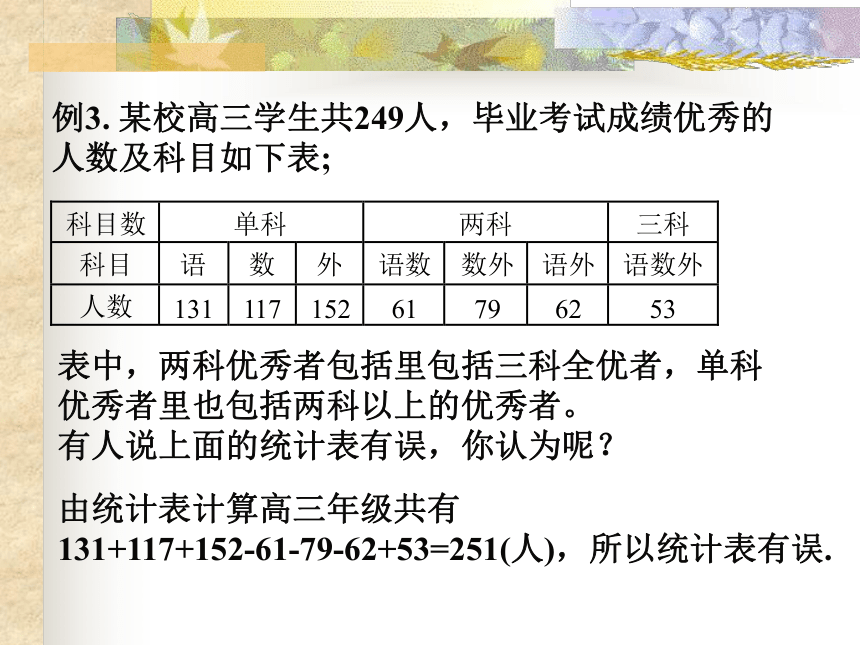
= card(A)+ card(B)-card(A∩B)能否推广?试写出三个集合类似公式.例3. 某校高三学生共249人,毕业考试成绩优秀的
人数及科目如下表;表中,两科优秀者包括里包括三科全优者,单科
优秀者里也包括两科以上的优秀者。
有人说上面的统计表有误,你认为呢?由统计表计算高三年级共有
131+117+152-61-79-62+53=251(人),所以统计表有误.例4. 在100个学生中,有美术爱好者63人,音乐
爱好者75人(并非每个学生都有爱好),对美术
和音乐都爱好的学生最多有多少人?最少有多少人?最多63人,最少38人.问题的提出:
无限集中元素的个数?!是不是所有的无限集都有相同的个数呢?
1.无限
(1)初识无限
(2)在有限集中,如何比较元素个数的多少?
理解无限的关键——一一对应
(3)无限集中元素的个数——基数
与此相关的一个定义:
若在一个集合与全体正整数集合之间
存在一一对应,则称这个集合是可数的。(4)几个令人吃惊的例子全体正整数和全体有理数一样多吗?全体正整数和全体整数一样多吗?部分=整体?!(5)问题的提出
是不是所有的无限集都有相同的基数呢?康托在1973年11月29日给戴德金的信中提出:11月29日-12月7日,康托给无限的理论奠定了基础。他创造了一种适用于无限集的新数体系——超限数,以解决无限集的基数比较问题。实数集(0,1)是不可数的。
无理数集是不可数的(有理数集可数)。是不是还存在数量上多于实数集的集合呢?实数集是不可数的 。—实数、一直线上的点、平面上的点
及高维空间的任一部分的点的基数。若在一个集合与全体正整数集合之间存在一一对应,则称这个集合是可数的。“数学中的无穷无尽,其诱人之处在于
它的最棘手的悖论能够盛开出美丽的
理论之花。”——E.Kasner and J.Newman集合论危机重重:2.罗素悖论 大多数集合不包含它自身为元素,这样的集我们
称之为“普通的”。有许多集可能包含它自身为元素,
例如集S定义如下:“凡是可以用不超过三十个字来
定义的集合是S的元素。”可以看到,S是包含它自身
为一元素的。这样的集我们称之为“非普通集”。我们
考查“所有普通集组成的集”,称它为C。那么C本身
是普通集还是非普通集?如果C是普通集,由于C定义
为包含所有普通集,它包含了它本身作为一个元素。
这样的话,C必须是非普通集。这是一个矛盾。因此
C必须是非普通集,但这时C包含了一个非普通集
(即C本身)为其元素,这与C只包含普通集的定义
相矛盾。因此,无论那一种情形,仅仅是C的存在,
就已经使我们陷入矛盾。罗素的理发师悖论其他一些悖论(1)芝诺悖论
1)二分法悖论
2)阿基里斯和乌龟
代数悖论:数理逻辑诞生 数理逻辑这门学科在第三次数学危机运动的过程中诞生,在十七世纪,算术因符号化促使了代数学的产生,代数使计算变得精确和方便,也使计算方法系统化。费尔马和笛卡儿的解析几何把几何学代数化,大大扩展了几何的领域,而且使得少数天才的推理变成机械化的步骤。这反映了代数学作为普遍科学方法的效力,于是笛卡儿尝试也把逻辑代数化。与笛卡儿同时代的英国哲学家霍布斯也认为推理带有计算性质,不过他并没有系统地发展这种思想。
??? 现在公认的数理逻辑创始人是莱布尼兹。他的目的是选出一种“通用代数”,其中把一切推理都化归为计算。实际上这正是数理逻辑的总纲领。他希望建立一套普遍的符号语言,这样就可以象数字一样进行演算,他的确将某些命题形式表达为符号形式,但他的工作只是一个开头,大部分没有发表,因此影响不大。
???
真正使逻辑代数化的是英国数学家布尔,他在1847年出版了《逻辑的数学分析》,给出了现代所谓的“布尔代数”的原型。布尔确信符号化会使逻辑变得严密。他的对象是事物的类,1表示全类,0表示空类;xy表示x和y的共同分子所组成的类,运算是逻辑乘法;x+y表示x和y两类所合成的类,运算是逻辑加法。
??? 布尔看出类的演算也可解释为命题的演算。当x、y不是类而是命题,则x=1表示的是命题 x为真,x=0表示命题x为假,1-x表示x的否定等等。显然布尔的演算构成一个代数系统,遵守着某些规律,这就是布尔代数。
非数值运算的推广
——集合运算
——语句运算康托的最大基数悖论、布拉里.福蒂悖论、
罗素悖论,动摇了整个数学的基础。给数学提供一个可靠的基础:
1)罗素的类型论
2)策梅罗的公理集合论(ZFS系统)
Z—策梅罗 F—弗兰克尔 S—斯科兰姆希尔伯特:哥德尔不完全性定理:
数理逻辑的大发展:
证明论;
递归论;
模型论;
公理集合论。作业:
查阅有关资料
试卷改错
《二教》不等式解法习题课的例题
集合中元素的个数例1 学校先举办了一次田径运动会,某班有8
名同学参赛,又举办了一次球类运动会。这个
班有12名同学参赛,两次运动会都参赛的有3
人。两次运动会中,这个班共有多少名同学参
赛?
分析:设A为田径运动会参赛的学生的集合,B
为球类运动会参赛的学生的集合。那么A∩B就
是两次运动会都参赛的学生的集合。
试分析 A∪B、 A、B、A∩B中元素个数的关系.解:设A={田径运动会参赛的学生},
B={球类运动会参赛的学生},那么,
A∩B={两次运动会都参赛的学生},
A∪B={参赛的学生}。
∴ card(A∪B)
= card(A)+ card(B)-card(A∩B)
=8+12-3=17。
答:两次运动会中,这个班共有17名同学参赛。
用图来求解 :例2.某班学生参加数学课外小组的人数是参加
物理课外小组的人数的2倍,同时参加两个课外
小组的人数是5人,至少参加一个课外活动小组
的人数为25人.试求参加数学小组、物理小组的
人数各是多少?参加数学小组20人,参加物理小组10人. card(A∪B)
= card(A)+ card(B)-card(A∩B)即 25=2x+x-5
x=10 card(A∪B)
= card(A)+ card(B)-card(A∩B)能否推广?试写出三个集合类似公式.例3. 某校高三学生共249人,毕业考试成绩优秀的
人数及科目如下表;表中,两科优秀者包括里包括三科全优者,单科
优秀者里也包括两科以上的优秀者。
有人说上面的统计表有误,你认为呢?由统计表计算高三年级共有
131+117+152-61-79-62+53=251(人),所以统计表有误.例4. 在100个学生中,有美术爱好者63人,音乐
爱好者75人(并非每个学生都有爱好),对美术
和音乐都爱好的学生最多有多少人?最少有多少人?最多63人,最少38人.问题的提出:
无限集中元素的个数?!是不是所有的无限集都有相同的个数呢?
1.无限
(1)初识无限
(2)在有限集中,如何比较元素个数的多少?
理解无限的关键——一一对应
(3)无限集中元素的个数——基数
与此相关的一个定义:
若在一个集合与全体正整数集合之间
存在一一对应,则称这个集合是可数的。(4)几个令人吃惊的例子全体正整数和全体有理数一样多吗?全体正整数和全体整数一样多吗?部分=整体?!(5)问题的提出
是不是所有的无限集都有相同的基数呢?康托在1973年11月29日给戴德金的信中提出:11月29日-12月7日,康托给无限的理论奠定了基础。他创造了一种适用于无限集的新数体系——超限数,以解决无限集的基数比较问题。实数集(0,1)是不可数的。
无理数集是不可数的(有理数集可数)。是不是还存在数量上多于实数集的集合呢?实数集是不可数的 。—实数、一直线上的点、平面上的点
及高维空间的任一部分的点的基数。若在一个集合与全体正整数集合之间存在一一对应,则称这个集合是可数的。“数学中的无穷无尽,其诱人之处在于
它的最棘手的悖论能够盛开出美丽的
理论之花。”——E.Kasner and J.Newman集合论危机重重:2.罗素悖论 大多数集合不包含它自身为元素,这样的集我们
称之为“普通的”。有许多集可能包含它自身为元素,
例如集S定义如下:“凡是可以用不超过三十个字来
定义的集合是S的元素。”可以看到,S是包含它自身
为一元素的。这样的集我们称之为“非普通集”。我们
考查“所有普通集组成的集”,称它为C。那么C本身
是普通集还是非普通集?如果C是普通集,由于C定义
为包含所有普通集,它包含了它本身作为一个元素。
这样的话,C必须是非普通集。这是一个矛盾。因此
C必须是非普通集,但这时C包含了一个非普通集
(即C本身)为其元素,这与C只包含普通集的定义
相矛盾。因此,无论那一种情形,仅仅是C的存在,
就已经使我们陷入矛盾。罗素的理发师悖论其他一些悖论(1)芝诺悖论
1)二分法悖论
2)阿基里斯和乌龟
代数悖论:数理逻辑诞生 数理逻辑这门学科在第三次数学危机运动的过程中诞生,在十七世纪,算术因符号化促使了代数学的产生,代数使计算变得精确和方便,也使计算方法系统化。费尔马和笛卡儿的解析几何把几何学代数化,大大扩展了几何的领域,而且使得少数天才的推理变成机械化的步骤。这反映了代数学作为普遍科学方法的效力,于是笛卡儿尝试也把逻辑代数化。与笛卡儿同时代的英国哲学家霍布斯也认为推理带有计算性质,不过他并没有系统地发展这种思想。
??? 现在公认的数理逻辑创始人是莱布尼兹。他的目的是选出一种“通用代数”,其中把一切推理都化归为计算。实际上这正是数理逻辑的总纲领。他希望建立一套普遍的符号语言,这样就可以象数字一样进行演算,他的确将某些命题形式表达为符号形式,但他的工作只是一个开头,大部分没有发表,因此影响不大。
???
真正使逻辑代数化的是英国数学家布尔,他在1847年出版了《逻辑的数学分析》,给出了现代所谓的“布尔代数”的原型。布尔确信符号化会使逻辑变得严密。他的对象是事物的类,1表示全类,0表示空类;xy表示x和y的共同分子所组成的类,运算是逻辑乘法;x+y表示x和y两类所合成的类,运算是逻辑加法。
??? 布尔看出类的演算也可解释为命题的演算。当x、y不是类而是命题,则x=1表示的是命题 x为真,x=0表示命题x为假,1-x表示x的否定等等。显然布尔的演算构成一个代数系统,遵守着某些规律,这就是布尔代数。
非数值运算的推广
——集合运算
——语句运算康托的最大基数悖论、布拉里.福蒂悖论、
罗素悖论,动摇了整个数学的基础。给数学提供一个可靠的基础:
1)罗素的类型论
2)策梅罗的公理集合论(ZFS系统)
Z—策梅罗 F—弗兰克尔 S—斯科兰姆希尔伯特:哥德尔不完全性定理:
数理逻辑的大发展:
证明论;
递归论;
模型论;
公理集合论。作业:
查阅有关资料
试卷改错
《二教》不等式解法习题课的例题
