【走进重高汇编】八下数学 第十九章 第一节 变量与函数训练卷
文档属性
| 名称 | 【走进重高汇编】八下数学 第十九章 第一节 变量与函数训练卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-30 00:00:00 | ||
图片预览



文档简介
【走进重高汇编】八下数学 第十九章 第一节 函数及其图像
一.选择题(共10小题)
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.当x=﹣3时,函数y=x2﹣3x﹣7的函数值为( )
A.﹣25 B.﹣7 C.8 D.11
3.下列各曲线中,表示y是x的函数的是( )
A. B. C. D.
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
5.地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10﹣来表示,如图,根据这个关系式,当d的值是900时,相应的T值是( )
A.4℃ B.5℃ C.6℃ D.16℃
6.函数y=的自变量x的取值范围是( )
A.x≤6 B.x<6且x≠2 C.x≤6且x≠2 D.x≥6
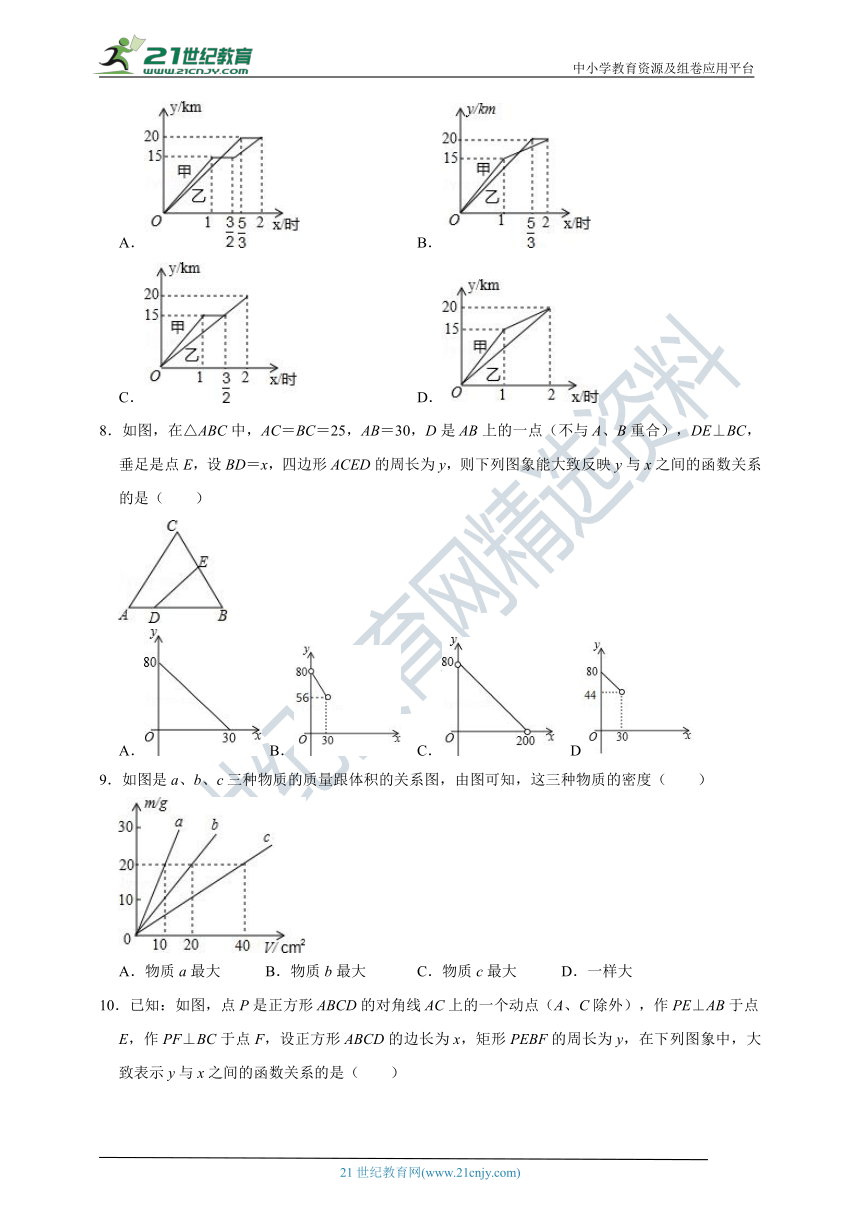
7.一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
8.如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A. B. C. D
9.如图是a、b、c三种物质的质量跟体积的关系图,由图可知,这三种物质的密度( )
A.物质a最大 B.物质b最大 C.物质c最大 D.一样大
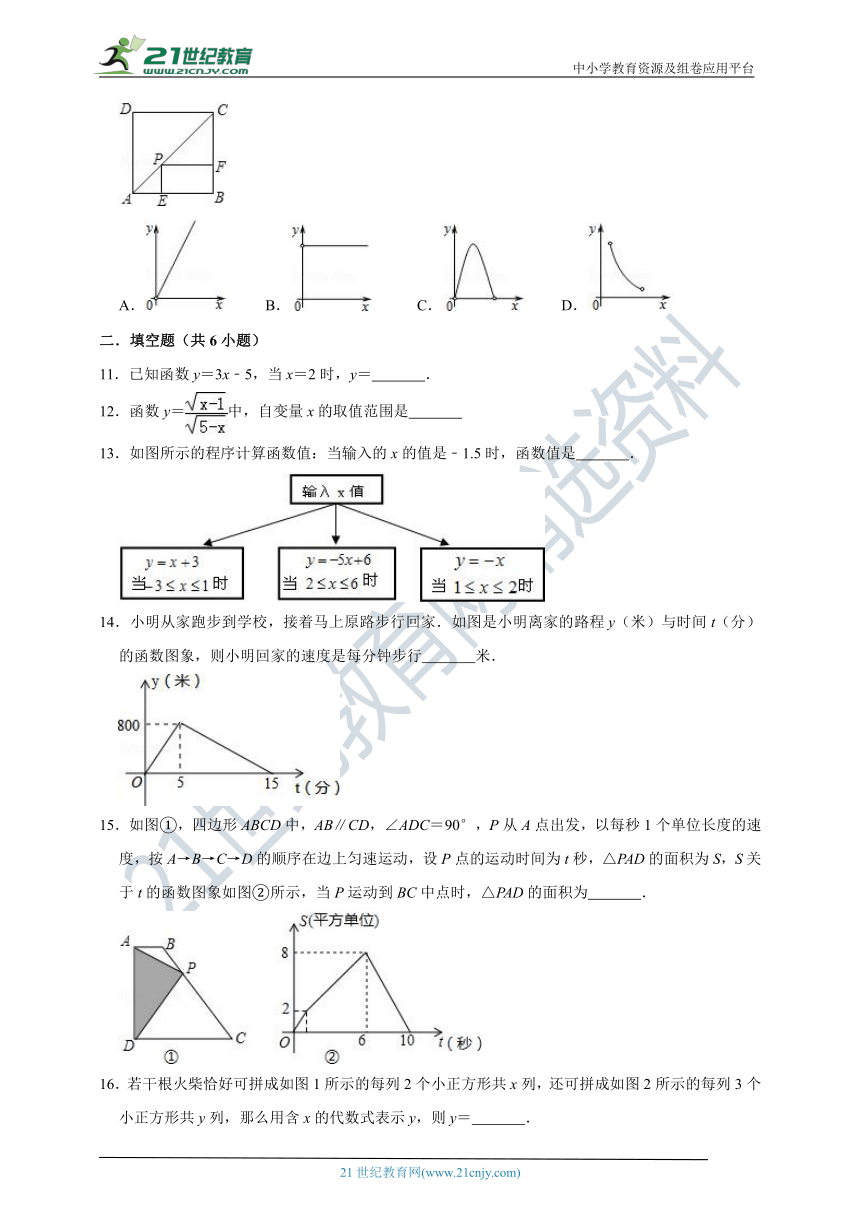
10.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
二.填空题(共6小题)
11.已知函数y=3x﹣5,当x=2时,y= .
12.函数y=中,自变量x的取值范围是
13.如图所示的程序计算函数值:当输入的x的值是﹣1.5时,函数值是 .
14.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
15.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
16.若干根火柴恰好可拼成如图1所示的每列2个小正方形共x列,还可拼成如图2所示的每列3个小正方形共y列,那么用含x的代数式表示y,则y= .
三.解答题(共7小题)
17.已知函数.
(1)求自变量x的取值范围;
(2)当x=1时的函数值.
18.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.
(1)根据如图,将表格补充完整.
白纸张数
1
2
3
4
5
纸条长度
40
110
145
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?
19.根据下面的运算程序,回答问题:
(1)若输入x=﹣3,请计算输出的结果y的值;
(2)若输入一个正数x时,输出y的值为12,请问输入的x值可能是多少?
20.某电动车厂2014年各月份生产电动车的数量情况如下表:
时间x/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量y/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
21.小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
22.如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
(1)当∠A变化时,求y与x之间的函数解析式,并指出自变量x的取值范围;
(2)当∠A=60°时,求∠P的度数;
(3)当∠P=125°时,求∠A的度数.
23.如图1,在矩形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
走进重高八下数学培优测试 第十九章 函数及其图像
参考答案与试题解析
一.选择题(共10小题)
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
【解答】解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:B.
2.当x=﹣3时,函数y=x2﹣3x﹣7的函数值为( )
A.﹣25 B.﹣7 C.8 D.11
【解答】解:∵函数y=x2﹣3x﹣7,
∴当x=﹣3时,y=(﹣3)2+9﹣7=11;
故选:D.
3.下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,所以B正确.
故选:B.
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
【解答】解:一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为y=10x+30,
故选:A.
5.地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10﹣来表示,如图,根据这个关系式,当d的值是900时,相应的T值是( )
A.4℃ B.5℃ C.6℃ D.16℃
【解答】解:d=900时,T=10﹣=10﹣6=4℃.
故选:A.
6.函数y=的自变量x的取值范围是( )
A.x≤6 B.x<6且x≠2 C.x≤6且x≠2 D.x≥6
【解答】解:由题意得,6﹣x≥0且x﹣2≠0,
解得x≤6且x≠2.
故选:C.
7.一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
【解答】解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选:A.
8.如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A. B.
C. D.
【解答】解:如图,作CM⊥AB于M.
∵CA=CB,AB=30,CM⊥AB,
∴AM=BM=15,CM==20
∵DE⊥BC,
∴∠DEB=∠CMB=90°,
∵∠B=∠B,
∴△DEB∽△CMB,
∴==,
∴==,
∴DE=,EB=,
∴四边形ACED的周长为y=25+(25﹣)++30﹣x=﹣x+80.
∵0<x<30,
∴图象是B.
故选:B.
9.如图是a、b、c三种物质的质量跟体积的关系图,由图可知,这三种物质的密度( )
A.物质a最大 B.物质b最大 C.物质c最大 D.一样大
【解答】解:由图象可知,当ma=mb=mc时,Va<Vb<Vc,
所以ρa>ρb>ρc.
故选:A.
10.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
【解答】解:由题意可得:△APE和△PCF都是等腰直角三角形.
∴AE=PE,PF=CF,那么矩形PEBF的周长等于2个正方形的边长.则y=2x,为正比例函数.
故选:A.
二.填空题(共6小题)
11.已知函数y=3x﹣5,当x=2时,y= 1 .
【解答】解:当x=2时,y=3×2﹣5=1.
故答案为:1.
12.函数y=中,自变量x的取值范围是 1≤X<5
【解答】解:根据题意得,
由①得,x≥1,
由②得,x<5,
∴不等式组的解集为1≤x<5,
∴自变量x的取值范围是1≤x<5.
故答案为:1≤x<5.
13.如图所示的程序计算函数值:当输入的x的值是﹣1.5时,函数值是 1.5 .
【解答】解:输入x=﹣1.5时,y=﹣1.5+3=1.5.
故答案为:1.5.
14.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 80 米.
【解答】解:通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
15.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 5 .
【解答】解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
当P点运动到BC中点时,BP=PC,
如图,作PQ⊥AD于点Q,
∴AB∥PQ∥CD,
∴PQ为梯形ABCD的中位线,
则PQ=(AB+CD),
∴△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
16.若干根火柴恰好可拼成如图1所示的每列2个小正方形共x列,还可拼成如图2所示的每列3个小正方形共y列,那么用含x的代数式表示y,则y= .
【解答】解:如图1,每列的火柴有7根,但两列之间有2根重叠,
∴图1中有火柴7x﹣2(x﹣1)=5x+2根;
如图2,每列的火柴有10根,但两列之间有3根重叠,
∴图2中有火柴10y﹣3(y﹣1)=7y+3根,
即7y+3=5x+2,
故y=.
故答案为:.
三.解答题(共7小题)
17.已知函数.
(1)求自变量x的取值范围;
(2)当x=1时的函数值.
【解答】解:(1)根据题意得:,
解得x<5;
(2)把x=1代入解析式可得:y=+=2﹣1=1;
答:自变量x的取值范围是x<5,当x=1时的函数值是1.
18.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.
(1)根据如图,将表格补充完整.
白纸张数
1
2
3
4
5
纸条长度
40
75
110
145
180
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?
【解答】解:(1)75,180;
(2)根据题意和所给图形可得出:
y=40x﹣5(x﹣1)=35x+5.
(3)不能.
把y=2016代入y=35x+5,
解得,不是整数,
所以不能.
19.根据下面的运算程序,回答问题:
(1)若输入x=﹣3,请计算输出的结果y的值;
(2)若输入一个正数x时,输出y的值为12,请问输入的x值可能是多少?
【解答】解:(1)∵x=﹣3<0,
∴y===2;
(2)若0≤x<2时,则=12,
解得x=,
若x≥2时,则x3﹣15=12,
解得x=3,
综上所述,输入的x的值可能是或3.
20.某电动车厂2014年各月份生产电动车的数量情况如下表:
时间x/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量y/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
【解答】解:(1)电动车的月产量y为随着时间的变化而变化,有一个时间就有唯一一个y,
月产量是时间的因变量;
(2)六月份常量最高,一月份常量最低;
(3)六月份和一月份相差最大,在一月份加紧生产,实现产量的增值.
21.小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
【解答】解:(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
(2)小明共用了30分钟到学校;
(3)修车前速度:3÷10=0.3千米/分,
修车后速度:5÷15=千米/分;
(4)8÷=(分种),
30﹣=≈3.3(分钟),
答:他比实际情况早到3.3分钟.
22.如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
(1)当∠A变化时,求y与x之间的函数解析式,并指出自变量x的取值范围;
(2)当∠A=60°时,求∠P的度数;
(3)当∠P=125°时,求∠A的度数.
【解答】解:(1)∵P是△ABC的内角的平分线交点,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB
=(∠ABC+∠ACB)
=(180°﹣x).
∵∠BOC=180°﹣(∠OBC+∠OCB),
∴∠BOC=180°﹣(180﹣x),
∴y=90°+(0<x<180).
(2)把∠A=x=60°代入y=90°+(0<x<180)得
y=90°+30°=120°,
所以∠P的度数为120°;
(3)把∠P=125°代入y=90°+(0<x<180)得
125°=90°+
解得,x=70°,
所以∠A的度数为70°.
23.如图1,在矩形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
【解答】解:(1)观察图象得,S△APQ=PA?AD=×(1×a)×6=24,
解得a=8(秒)
b==2(厘米/秒)
(22﹣8)c=(12×2+6)﹣2×8
解得c=1(厘米/秒)
(2)依题意得:y1=1×8+2(x﹣8),
即:y1=2x﹣8(x>8),
y2=(30﹣2×8)﹣1×(x﹣8)
=22﹣x(x>8)
又据题意,当y1=y2,P与Q相遇,即
即2x﹣8=(22﹣x),
解得x=10.
故出发10s时P、Q相遇.
一.选择题(共10小题)
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.当x=﹣3时,函数y=x2﹣3x﹣7的函数值为( )
A.﹣25 B.﹣7 C.8 D.11
3.下列各曲线中,表示y是x的函数的是( )
A. B. C. D.
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
5.地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10﹣来表示,如图,根据这个关系式,当d的值是900时,相应的T值是( )
A.4℃ B.5℃ C.6℃ D.16℃
6.函数y=的自变量x的取值范围是( )
A.x≤6 B.x<6且x≠2 C.x≤6且x≠2 D.x≥6
7.一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
8.如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A. B. C. D
9.如图是a、b、c三种物质的质量跟体积的关系图,由图可知,这三种物质的密度( )
A.物质a最大 B.物质b最大 C.物质c最大 D.一样大
10.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
二.填空题(共6小题)
11.已知函数y=3x﹣5,当x=2时,y= .
12.函数y=中,自变量x的取值范围是
13.如图所示的程序计算函数值:当输入的x的值是﹣1.5时,函数值是 .
14.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
15.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
16.若干根火柴恰好可拼成如图1所示的每列2个小正方形共x列,还可拼成如图2所示的每列3个小正方形共y列,那么用含x的代数式表示y,则y= .
三.解答题(共7小题)
17.已知函数.
(1)求自变量x的取值范围;
(2)当x=1时的函数值.
18.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.
(1)根据如图,将表格补充完整.
白纸张数
1
2
3
4
5
纸条长度
40
110
145
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?
19.根据下面的运算程序,回答问题:
(1)若输入x=﹣3,请计算输出的结果y的值;
(2)若输入一个正数x时,输出y的值为12,请问输入的x值可能是多少?
20.某电动车厂2014年各月份生产电动车的数量情况如下表:
时间x/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量y/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
21.小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
22.如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
(1)当∠A变化时,求y与x之间的函数解析式,并指出自变量x的取值范围;
(2)当∠A=60°时,求∠P的度数;
(3)当∠P=125°时,求∠A的度数.
23.如图1,在矩形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
走进重高八下数学培优测试 第十九章 函数及其图像
参考答案与试题解析
一.选择题(共10小题)
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
【解答】解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:B.
2.当x=﹣3时,函数y=x2﹣3x﹣7的函数值为( )
A.﹣25 B.﹣7 C.8 D.11
【解答】解:∵函数y=x2﹣3x﹣7,
∴当x=﹣3时,y=(﹣3)2+9﹣7=11;
故选:D.
3.下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,所以B正确.
故选:B.
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
【解答】解:一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为y=10x+30,
故选:A.
5.地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10﹣来表示,如图,根据这个关系式,当d的值是900时,相应的T值是( )
A.4℃ B.5℃ C.6℃ D.16℃
【解答】解:d=900时,T=10﹣=10﹣6=4℃.
故选:A.
6.函数y=的自变量x的取值范围是( )
A.x≤6 B.x<6且x≠2 C.x≤6且x≠2 D.x≥6
【解答】解:由题意得,6﹣x≥0且x﹣2≠0,
解得x≤6且x≠2.
故选:C.
7.一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
【解答】解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选:A.
8.如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A. B.
C. D.
【解答】解:如图,作CM⊥AB于M.
∵CA=CB,AB=30,CM⊥AB,
∴AM=BM=15,CM==20
∵DE⊥BC,
∴∠DEB=∠CMB=90°,
∵∠B=∠B,
∴△DEB∽△CMB,
∴==,
∴==,
∴DE=,EB=,
∴四边形ACED的周长为y=25+(25﹣)++30﹣x=﹣x+80.
∵0<x<30,
∴图象是B.
故选:B.
9.如图是a、b、c三种物质的质量跟体积的关系图,由图可知,这三种物质的密度( )
A.物质a最大 B.物质b最大 C.物质c最大 D.一样大
【解答】解:由图象可知,当ma=mb=mc时,Va<Vb<Vc,
所以ρa>ρb>ρc.
故选:A.
10.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
【解答】解:由题意可得:△APE和△PCF都是等腰直角三角形.
∴AE=PE,PF=CF,那么矩形PEBF的周长等于2个正方形的边长.则y=2x,为正比例函数.
故选:A.
二.填空题(共6小题)
11.已知函数y=3x﹣5,当x=2时,y= 1 .
【解答】解:当x=2时,y=3×2﹣5=1.
故答案为:1.
12.函数y=中,自变量x的取值范围是 1≤X<5
【解答】解:根据题意得,
由①得,x≥1,
由②得,x<5,
∴不等式组的解集为1≤x<5,
∴自变量x的取值范围是1≤x<5.
故答案为:1≤x<5.
13.如图所示的程序计算函数值:当输入的x的值是﹣1.5时,函数值是 1.5 .
【解答】解:输入x=﹣1.5时,y=﹣1.5+3=1.5.
故答案为:1.5.
14.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 80 米.
【解答】解:通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
15.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 5 .
【解答】解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
当P点运动到BC中点时,BP=PC,
如图,作PQ⊥AD于点Q,
∴AB∥PQ∥CD,
∴PQ为梯形ABCD的中位线,
则PQ=(AB+CD),
∴△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
16.若干根火柴恰好可拼成如图1所示的每列2个小正方形共x列,还可拼成如图2所示的每列3个小正方形共y列,那么用含x的代数式表示y,则y= .
【解答】解:如图1,每列的火柴有7根,但两列之间有2根重叠,
∴图1中有火柴7x﹣2(x﹣1)=5x+2根;
如图2,每列的火柴有10根,但两列之间有3根重叠,
∴图2中有火柴10y﹣3(y﹣1)=7y+3根,
即7y+3=5x+2,
故y=.
故答案为:.
三.解答题(共7小题)
17.已知函数.
(1)求自变量x的取值范围;
(2)当x=1时的函数值.
【解答】解:(1)根据题意得:,
解得x<5;
(2)把x=1代入解析式可得:y=+=2﹣1=1;
答:自变量x的取值范围是x<5,当x=1时的函数值是1.
18.将长为40cm,宽为15cm的长方形白纸,按如图所示的方法粘合起来,粘合部分宽为5cm.
(1)根据如图,将表格补充完整.
白纸张数
1
2
3
4
5
纸条长度
40
75
110
145
180
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2016cm吗?为什么?
【解答】解:(1)75,180;
(2)根据题意和所给图形可得出:
y=40x﹣5(x﹣1)=35x+5.
(3)不能.
把y=2016代入y=35x+5,
解得,不是整数,
所以不能.
19.根据下面的运算程序,回答问题:
(1)若输入x=﹣3,请计算输出的结果y的值;
(2)若输入一个正数x时,输出y的值为12,请问输入的x值可能是多少?
【解答】解:(1)∵x=﹣3<0,
∴y===2;
(2)若0≤x<2时,则=12,
解得x=,
若x≥2时,则x3﹣15=12,
解得x=3,
综上所述,输入的x的值可能是或3.
20.某电动车厂2014年各月份生产电动车的数量情况如下表:
时间x/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量y/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
【解答】解:(1)电动车的月产量y为随着时间的变化而变化,有一个时间就有唯一一个y,
月产量是时间的因变量;
(2)六月份常量最高,一月份常量最低;
(3)六月份和一月份相差最大,在一月份加紧生产,实现产量的增值.
21.小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
【解答】解:(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
(2)小明共用了30分钟到学校;
(3)修车前速度:3÷10=0.3千米/分,
修车后速度:5÷15=千米/分;
(4)8÷=(分种),
30﹣=≈3.3(分钟),
答:他比实际情况早到3.3分钟.
22.如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
(1)当∠A变化时,求y与x之间的函数解析式,并指出自变量x的取值范围;
(2)当∠A=60°时,求∠P的度数;
(3)当∠P=125°时,求∠A的度数.
【解答】解:(1)∵P是△ABC的内角的平分线交点,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB
=(∠ABC+∠ACB)
=(180°﹣x).
∵∠BOC=180°﹣(∠OBC+∠OCB),
∴∠BOC=180°﹣(180﹣x),
∴y=90°+(0<x<180).
(2)把∠A=x=60°代入y=90°+(0<x<180)得
y=90°+30°=120°,
所以∠P的度数为120°;
(3)把∠P=125°代入y=90°+(0<x<180)得
125°=90°+
解得,x=70°,
所以∠A的度数为70°.
23.如图1,在矩形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
【解答】解:(1)观察图象得,S△APQ=PA?AD=×(1×a)×6=24,
解得a=8(秒)
b==2(厘米/秒)
(22﹣8)c=(12×2+6)﹣2×8
解得c=1(厘米/秒)
(2)依题意得:y1=1×8+2(x﹣8),
即:y1=2x﹣8(x>8),
y2=(30﹣2×8)﹣1×(x﹣8)
=22﹣x(x>8)
又据题意,当y1=y2,P与Q相遇,即
即2x﹣8=(22﹣x),
解得x=10.
故出发10s时P、Q相遇.
