【走进重高汇编】八下数学 第十九章 第三节 一次函数的应用训练卷
文档属性
| 名称 | 【走进重高汇编】八下数学 第十九章 第三节 一次函数的应用训练卷 | 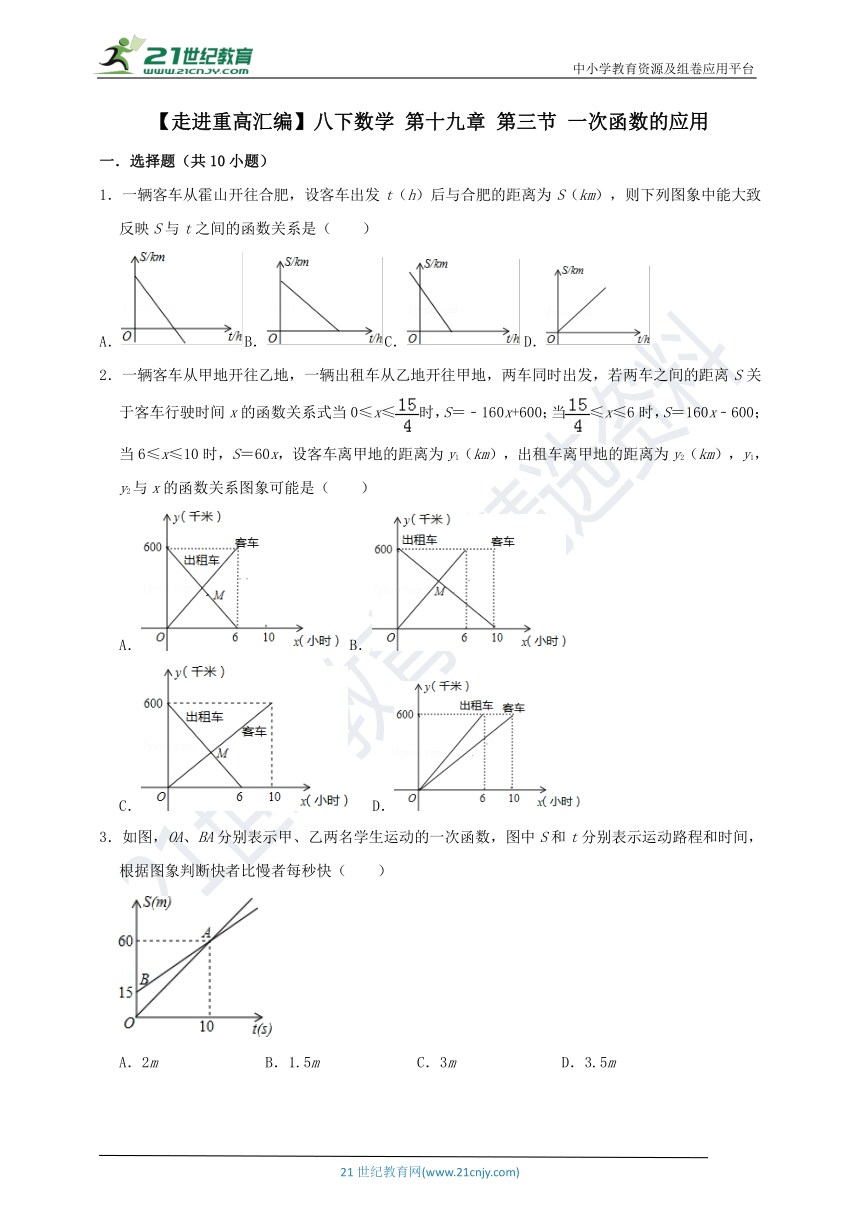 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-30 21:13:57 | ||
图片预览





文档简介
【走进重高汇编】八下数学 第十九章 第三节 一次函数的应用
一.选择题(共10小题)
1.一辆客车从霍山开往合肥,设客车出发t(h)后与合肥的距离为S(km),则下列图象中能大致反映S与t之间的函数关系是( )
A.B.C. D.
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,若两车之间的距离S关于客车行驶时间x的函数关系式当0≤x≤时,S=﹣160x+600;当≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
A. B.
C. D.
3.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( )
A.2m B.1.5m C.3m D.3.5m
4.有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为( )
A.10厘米 B.13.5厘米 C.14厘米 D.14.5厘米
5.某地电话拨号入网有两种收费方式:A计时制:每分0.05元;B包月制:每月50元.此外,每一种上网方式都得加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,你认为采用哪种收费方式较为合算?( )
A.计时制 B.包月制 C.两种一样 D.不确定
6.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
根据上表解决下面这个实际问题:姚明的身高是226厘米,他的指距为( )
A.26.8厘米 B.26.9厘米 C.27.5厘米 D.27.3厘米
7.已知:一次函数y=ax+b中的自变量x与函数y的对应值如下表所示:
x
…
﹣1
0
…
y
…
﹣π
1
…
则关于x的方程ax+b=0的解满足( )
A.x<1 B.﹣1<x<0 C.0<x<1 D.x>1
8.当﹣1≤x≤2时,函数y=ax+6满足y<10,则常数a的取值范围是( )
A.﹣4<a<0 B.0<a<2
C.﹣4<a<2且a≠0 D.﹣4<a<2
9.已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市.如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:①甲车出发时的速度是60千米/时;
②乙车的速度是96千米/时;③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市时乙车已返回A市2小时20分钟.其中正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
10.如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=﹣2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=,AB=2,则m,n的值分别是( )
A.3,2 B.2,1 C. D.1,
二.填空题(共6小题)
11.长方形的长为3cm,宽为2cm,若长增加xcm,则它的面积S(cm2)与x(cm)之间的函数关系式是 ,它是 函数,它的图象是 .
12.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系式如图所示,其中BA是线段,且BA∥x轴,AC是射线,若小李12月份上网费用为84元,则他在该月份上网时间是 小时.
13.已知一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),则a+b= .
14.孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,﹣1),则b的正确值是 .
15.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有 米.
16.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An+1作x轴的垂线交一次函数的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的坐标是 .
三.解答题(共7小题)
17.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1).
(1)求一次函数的解析式;
(2)请直接写出不等式组﹣1<kx+b<2x的解集.
18.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=﹣1交于点D,C为直线y轴的交点.
(1)求直线AB的解析式;
(2)求S△ADC.
19.某厂准备购买A、B、C三种配件共1000件,要求购买时C配件的件数是A配件件数的4倍,B配件不超过400件,且每种配件必须买,三种配件的价格如下表:
配件
A
B
C
价格(元/件)
30
50
80
假设购买A配件x(件),买全配件所需的总费用为y(元).
(1)求y与x之间的函数关系式;
(2)要使买全配件所需的总费用最少,三种配件应各买多少件?所需总费用最少多少元?
20.小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.下图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.
(1)分别求出AB段和BC段图象所在直线的解析式.
(2)到达旅游目的地后,司机说:“今日改走高速公路后比往日全走普通公路省油6升”,求此时油箱内的余油量.(假设走高速公路和走普通公路的路程一样)
(3)已知出租车在高速公路上匀速行驶的速度是100千米/小时,求出租车在高速公路上行驶的时间.
21.某项工程若由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲乙两人合作,则需12天完成.
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
22.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:
(1)自行车队行驶的速度是 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
23.规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k?b≠0,且|k|≠|b|)为互助一次函数,例如和就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
(1)如图(1),当k=﹣1,b=3时,
①直接写出P点坐标:P ;
②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;
(2)如图(2),已知点M(﹣1,2),N(﹣2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.
【走进重高汇编】八下数学 第十九章 第三节 一次函数的应用
参考答案与试题解析
一.选择题(共10小题)
1.一辆客车从霍山开往合肥,设客车出发t(h)后与合肥的距离为S(km),则下列图象中能大致反映S与t之间的函数关系是( )
A. B.
C. D.
【解答】解:火车是匀速行驶的,图象为线段,s表示火车从霍山出发后与合肥的距离,s会逐渐减小为0;A、C、D都不符.
故选:B.
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,若两车之间的距离S关于客车行驶时间x的函数关系式当0≤x≤时,S=﹣160x+600;当≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
A. B.
C. D.
【解答】解:∵一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,
∴两车相向运动,D图象不符合;
∵当6≤x≤10时,S=60x,
∴当x=6时,快车到达目的地,当x=10时,慢车到达目的地,A图象不符合;
又∵S关于x的函数关系式是两车之间的距离关于客车行驶时间的函数关系式,
∴客车用了10小时达到目的地,C图象符合题意.
故选:C.
3.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( )
A.2m B.1.5m C.3m D.3.5m
【解答】解:快者的速度为60÷10=6m/s,
慢者的速度为(60﹣15)÷10=4.5m/s,∴6﹣4.5=1.5,故选:B.
4.有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为( )
A.10厘米 B.13.5厘米 C.14厘米 D.14.5厘米
【解答】答:由表中关系可以得到,弹簧长度y(厘米)与称重x(千克)的关系是一次函数关系,
∴设弹簧长度y(厘米)与称重x(千克)的关系式为y=kx+b,
根据表格中提供的数据得当x=1时,y=4.5;当x=2时,y=5.5;
∴,解得:,∴解析式为y=3.5+x,
当弹簧最长时就是所挂重物最重时,此时x=10,∴y=3.5+10=13.5,
故弹簧最长为13.5厘米.故选:B.
5.某地电话拨号入网有两种收费方式:A计时制:每分0.05元;B包月制:每月50元.此外,每一种上网方式都得加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,你认为采用哪种收费方式较为合算?( )
A.计时制 B.包月制 C.两种一样 D.不确定
【解答】解:根据题意,计时制 y=(0.05+0.02)?60x=4.2x;
包月制 y=50+0.02?60x=50+1.2x;
当x=20时,计时制费用 y=4.2×20=84(元);
包月制费用 y=50+1.2×20=74(元),
所以 一个月内上网的时间为20小时,采用包月制较为合算.
故选:B.
6.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
根据上表解决下面这个实际问题:姚明的身高是226厘米,他的指距为( )
A.26.8厘米 B.26.9厘米 C.27.5厘米 D.27.3厘米
【解答】解:设这个一次函数的解析式是:y=kx+b,
,解得:,
一次函数的解析式是:y=9x﹣20,当y=226时,9x﹣20=226,x=27.3.故选:D.
7.已知:一次函数y=ax+b中的自变量x与函数y的对应值如下表所示:
x
…
﹣1
0
…
y
…
﹣π
1
…
则关于x的方程ax+b=0的解满足( )
A.x<1 B.﹣1<x<0 C.0<x<1 D.x>1
【解答】解:∵x=﹣1时,y=﹣π;x=0时,y=1,
∴﹣1<x<0时,y的值由负到正,∴关于x的方程ax+b=0的解满足﹣1<x<0.
故选:B.
8.当﹣1≤x≤2时,函数y=ax+6满足y<10,则常数a的取值范围是( )
A.﹣4<a<0 B.0<a<2
C.﹣4<a<2且a≠0 D.﹣4<a<2
【解答】解:由题意a≠0
当a<0时,函数y=ax+6为一次函数,它是递减的,
当﹣1≤x≤2时,y<10.
则有当x=﹣1,y=ax+6=﹣a+6<10,
解得:a>﹣4,
故此时:﹣4<a<0;
当a>0时,函数y=ax+6为一次函数,它是递增的,
当x=2,y=ax+6=2a+6<10,解得a<2;
故可得此时0<a<2;
所以﹣4<a<2,且a≠0.
故选:C.
9.已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市.如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
①甲车出发时的速度是60千米/时;
②乙车的速度是96千米/时;
③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市时乙车已返回A市2小时20分
钟.其中正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
【解答】解:①甲车提速后的速度为:80÷2×1.5=60(千米/时),故①正确;
②乙车的速度为80×2÷(4﹣2﹣)=96(千米/时),故②正确;
③∵修车用了20分钟,
∴点C的横坐标为4﹣(4﹣2﹣)÷2=,
∴点C的坐标为(,80).
设乙车返回时y与x的函数关系式为y=kx+b,
将点(,80)、(4,0)代入y=kx+b,
,
解得,
∴乙车返回时y与x的函数关系式为y=﹣96x+384,故③正确;
④甲车到达B市的时间为+(260﹣80)÷60=(小时),
∵﹣4=(小时),
∴甲车到达B市时乙车已返回A市小时,故④错误.
综上所述:正确的结论有①②③.
故选:C.
10.如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=﹣2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=,AB=2,则m,n的值分别是( )
A.3,2 B.2,1 C. D.1,
【解答】解:根据题意得:点A的坐标为(﹣n,0),点Q的坐标为(0,n),点B的坐标为(,0),
∵点P是PA与PB的交点,
∴,
解得:,
∴点P的坐标为:(,),
∵AB=2,
∴OA+OB=n+==2,
∴m+2n=4,
∵S四边形PQOB=,
∴S△PAB﹣S△AOQ=×2×﹣n×n=﹣n2=,
解得:n=1,
∴m=2.
故选:B.
二.填空题(共6小题)
11.长方形的长为3cm,宽为2cm,若长增加xcm,则它的面积S(cm2)与x(cm)之间的函数关系式是 S=2x+6 ,它是 一次 函数,它的图象是 直线 .
【解答】解:∵长方形的长为3cm,宽为2cm,长增加xcm,
∴长为:(3+x)cm,
∴它的面积S(cm2)与x(cm)之间的函数关系式是:S=2(3+x)=2x+6.
∴此函数是一次函数,图象是直线,
故答案为:S=2x+6,一次,直线.
12.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系式如图所示,其中BA是线段,且BA∥x轴,AC是射线,若小李12月份上网费用为84元,则他在该月份上网时间是 38 小时.
【解答】解:当x≥30时,设函数关系式为y=kx+b,
则,
解得.
所以y=3x﹣30;
由84=3x﹣30
解得:x=38,所以他在该月份上网时间是38小时.
故答案为:38.
13.已知一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),则a+b= 16 .
【解答】解:∵一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),
∴﹣m+a=8①,m+b=8②,
①+②得:a+b=16.
故填16.
14.孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,﹣1),则b的正确值是 ﹣13 .
【解答】解:依题意得:2=﹣k+6,k=4;
又∵﹣1=3×4+b,
∴b=﹣13,
故答案为:﹣13.
15.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有 40 米.
【解答】解:设乙的速度为x米/秒,根据图象得到360+180×15=180x,
解得x=17,
乙到达终点所用时间为:3400÷17=200s,
则此时甲离终点的距离为:3400﹣(360+15×200)=40m.
故答案为:40.
16.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An+1作x轴的垂线交一次函数的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的坐标是 (n+,) .
【解答】解:由已知得A1,A2,A3,…的坐标为:(1,0),(2,0),(3,0),…,
又得作x轴的垂线交一次函数y=x的图象于点B1,B2,B3,…的坐标分别为(1,),(2,1),(3,),….
由此可推出An,Bn,An+1,Bn+1四点的坐标为,(n,0),(n,),(n+1,0),(n+1,).
所以得直线AnBn+1和An+1Bn的直线方程分别为:
y﹣0=(x﹣n)+0,
y﹣0=(x﹣n﹣1)+0,
即,
解得:
,
故答案为:(n+,).
三.解答题(共7小题)
17.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1).
(1)求一次函数的解析式;
(2)请直接写出不等式组﹣1<kx+b<2x的解集.
【解答】解:(1)∵点A(m,2)在正比例函数y=2x的图象上,
∴2=2m,解得:m=1,
∴点A的坐标为(1,2).
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
,解得:,
∴一次函数的解析式为y=x+1.
(2)∵在y=x+1中,1>0,
∴y值随x值的增大而增大,
∴不等式﹣1<x+1的解集为x>﹣2.
观察函数图象可知,当x>1时,一次函数y=x+1的图象在正比例函数y=2x的图象的下方,
∴不等式组﹣1<x+1<2x的解集为x>1.
18.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=﹣1交于点D,C为直线y轴的交点.
(1)求直线AB的解析式;
(2)求S△ADC.
【解答】解:(1)设直线AB的解析式为y=kx+b,
把A(0,2),B(3,0)分别代入得,解得,
所以直线AB的解析式为y=﹣x+2;
(2)当x=0时,y=﹣1=﹣1,则C(0,﹣1),
解方程组得,则D(2,),
所以S△ADC=×(2+1)×2=3.
19.某厂准备购买A、B、C三种配件共1000件,要求购买时C配件的件数是A配件件数的4倍,B配件不超过400件,且每种配件必须买,三种配件的价格如下表:
配件
A
B
C
价格(元/件)
30
50
80
假设购买A配件x(件),买全配件所需的总费用为y(元).
(1)求y与x之间的函数关系式;
(2)要使买全配件所需的总费用最少,三种配件应各买多少件?所需总费用最少多少元?
【解答】解:(1)设购买A配件x(件),则C配件购买4x件,B配件购买(1000﹣5x)件,由题意,得
y=30x+80×4x+50(1000﹣5x),
y=100x+50000.
答:y与x之间的函数关系式为y=100x+50000;
(2)∵B配件不超过400件,
∴1000﹣5x≤400,
∴x≥120.
∵y=100x+50000,
∴k=100>0,
∴x=120时,y最大=62000.
∴B配件为:1000﹣120×5=400,
C配件为:120×4=480.
答:购买A配件120件,B配件400件,C配件480件时,总费用最少为62000元.
20.小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.下图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.
(1)分别求出AB段和BC段图象所在直线的解析式.
(2)到达旅游目的地后,司机说:“今日改走高速公路后比往日全走普通公路省油6升”,求此时油箱内的余油量.(假设走高速公路和走普通公路的路程一样)
(3)已知出租车在高速公路上匀速行驶的速度是100千米/小时,求出租车在高速公路上行驶的时间.
【解答】解(1)设AB段所在直线的解析式为Q=k1s+b1,
则据图象可得,解得.
∴AB段所在直线的解析式为.
又设BC图象所在直线的解析为Q=k2s+b2,
同样可得 解得.
∴BC段所在直线的解析式为.
(2)据题意可得,解得s=350(千米).
∴当s=350时,.
(3)出租车在高速公路上行驶的时间为:(350﹣50)÷100=3(小时).
21.某项工程若由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲乙两人合作,则需12天完成.
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
【解答】解:(1)设乙单独完成需a天,则甲单独完成需1.5a天,
根据题意列:+=,
解得,a=20,
经检验:a=20是所列方程根,且符合题意,
所以1.5a=30,
答:甲、乙两队单独完成分别需30天,20天;
(2)设甲乙合作完成余下部分所需时间为w天,列:++=1,
解得,w=﹣x+12,
∴y=x+(1+2.5)(﹣x+12)=﹣x+42;
(3)由题可得15≤x﹣x+12≤18,
解得,5≤x≤10,
∵﹣<0,
∴y随x的增大而减小,
∴当x=10时,y最小=﹣×10+42=38,
此时,甲先施工10天,再甲乙合作8天,费用最低为38万元.
22.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:
(1)自行车队行驶的速度是 24 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
【解答】解:(1)由题意得
自行车队行驶的速度是:72÷3=24km/h.
故答案为:24;
(2)由题意得
邮政车的速度为:24×2.5=60km/h.
设邮政车出发a小时两车相遇,由题意得
24(a+1)=60a,
解得:a=.
答:邮政车出发小时与自行车队首次相遇;
(3)由题意,得
邮政车到达丙地的时间为:135÷60=,
∴邮政车从丙地出发的时间为:,
∴B(,135),C(7.5,0).
自行车队到达丙地的时间为:135÷24+0.5=+0.5=,
∴D(,135).
设BC的解析式为y1=k1x+b1,由题意得
,
∴,
∴y1=﹣60x+450,
设ED的解析式为y2=k2x+b2,由题意得
,
解得:,
∴y2=24x﹣12.
当y1=y2时,
﹣60x+450=24x﹣12,
解得:x=5.5.
y1=﹣60×5.5+450=120.
答:邮政车在返程途中与自行车队再次相遇时的地点距离甲地120km.
23.规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k?b≠0,且|k|≠|b|)为互助一次函数,例如和就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
(1)如图(1),当k=﹣1,b=3时,
①直接写出P点坐标:P (1,2) ;
②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;
(2)如图(2),已知点M(﹣1,2),N(﹣2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.
【解答】解:(1)①∵一次函数y=kx+b和它的互助一次函数的图象交于P点,
k=﹣1,b=3时,
∴,
解得:,
∴P(1,2);
故答案为:(1,2);
②如图(1),连接OQ,
∵y=﹣x+3与y=3x﹣1的图象l1,l2与x轴,y轴分别交于A,B点和C,D点.
∴A(3,0),B(0,3),C(,0),D(0,﹣1).
∵Q(m,3m﹣1),(),
∴S=S△OBQ+S△OCQ==.
∴S△BCQ=S﹣S△BOC==,
而S△ACP==,
由S△BCQ=S△ACP,得 =,
解得m=;
(2)由,
解得 ,即P(1,k+b),
∴随着k,b值的变化,点P在直线x=1上运动,MP+NP的值随之发生变化.
如图(2),作点N(﹣2,0)关于直线x=1的对称点N′(4,0),
连接MN′交直线x=1于点P,则此时MP+NP取得最小值.
设直线MN′的解析式为y=cx+d,依题意,
解得 ,
∴直线MN′的解析式为.
令x=1,则,
∴P(1,),
即 使MP+NP取最小值时的P点坐标为(1,).
一.选择题(共10小题)
1.一辆客车从霍山开往合肥,设客车出发t(h)后与合肥的距离为S(km),则下列图象中能大致反映S与t之间的函数关系是( )
A.B.C. D.
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,若两车之间的距离S关于客车行驶时间x的函数关系式当0≤x≤时,S=﹣160x+600;当≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
A. B.
C. D.
3.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( )
A.2m B.1.5m C.3m D.3.5m
4.有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为( )
A.10厘米 B.13.5厘米 C.14厘米 D.14.5厘米
5.某地电话拨号入网有两种收费方式:A计时制:每分0.05元;B包月制:每月50元.此外,每一种上网方式都得加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,你认为采用哪种收费方式较为合算?( )
A.计时制 B.包月制 C.两种一样 D.不确定
6.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
根据上表解决下面这个实际问题:姚明的身高是226厘米,他的指距为( )
A.26.8厘米 B.26.9厘米 C.27.5厘米 D.27.3厘米
7.已知:一次函数y=ax+b中的自变量x与函数y的对应值如下表所示:
x
…
﹣1
0
…
y
…
﹣π
1
…
则关于x的方程ax+b=0的解满足( )
A.x<1 B.﹣1<x<0 C.0<x<1 D.x>1
8.当﹣1≤x≤2时,函数y=ax+6满足y<10,则常数a的取值范围是( )
A.﹣4<a<0 B.0<a<2
C.﹣4<a<2且a≠0 D.﹣4<a<2
9.已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市.如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:①甲车出发时的速度是60千米/时;
②乙车的速度是96千米/时;③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市时乙车已返回A市2小时20分钟.其中正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
10.如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=﹣2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=,AB=2,则m,n的值分别是( )
A.3,2 B.2,1 C. D.1,
二.填空题(共6小题)
11.长方形的长为3cm,宽为2cm,若长增加xcm,则它的面积S(cm2)与x(cm)之间的函数关系式是 ,它是 函数,它的图象是 .
12.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系式如图所示,其中BA是线段,且BA∥x轴,AC是射线,若小李12月份上网费用为84元,则他在该月份上网时间是 小时.
13.已知一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),则a+b= .
14.孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,﹣1),则b的正确值是 .
15.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有 米.
16.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An+1作x轴的垂线交一次函数的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的坐标是 .
三.解答题(共7小题)
17.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1).
(1)求一次函数的解析式;
(2)请直接写出不等式组﹣1<kx+b<2x的解集.
18.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=﹣1交于点D,C为直线y轴的交点.
(1)求直线AB的解析式;
(2)求S△ADC.
19.某厂准备购买A、B、C三种配件共1000件,要求购买时C配件的件数是A配件件数的4倍,B配件不超过400件,且每种配件必须买,三种配件的价格如下表:
配件
A
B
C
价格(元/件)
30
50
80
假设购买A配件x(件),买全配件所需的总费用为y(元).
(1)求y与x之间的函数关系式;
(2)要使买全配件所需的总费用最少,三种配件应各买多少件?所需总费用最少多少元?
20.小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.下图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.
(1)分别求出AB段和BC段图象所在直线的解析式.
(2)到达旅游目的地后,司机说:“今日改走高速公路后比往日全走普通公路省油6升”,求此时油箱内的余油量.(假设走高速公路和走普通公路的路程一样)
(3)已知出租车在高速公路上匀速行驶的速度是100千米/小时,求出租车在高速公路上行驶的时间.
21.某项工程若由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲乙两人合作,则需12天完成.
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
22.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:
(1)自行车队行驶的速度是 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
23.规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k?b≠0,且|k|≠|b|)为互助一次函数,例如和就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
(1)如图(1),当k=﹣1,b=3时,
①直接写出P点坐标:P ;
②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;
(2)如图(2),已知点M(﹣1,2),N(﹣2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.
【走进重高汇编】八下数学 第十九章 第三节 一次函数的应用
参考答案与试题解析
一.选择题(共10小题)
1.一辆客车从霍山开往合肥,设客车出发t(h)后与合肥的距离为S(km),则下列图象中能大致反映S与t之间的函数关系是( )
A. B.
C. D.
【解答】解:火车是匀速行驶的,图象为线段,s表示火车从霍山出发后与合肥的距离,s会逐渐减小为0;A、C、D都不符.
故选:B.
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,若两车之间的距离S关于客车行驶时间x的函数关系式当0≤x≤时,S=﹣160x+600;当≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
A. B.
C. D.
【解答】解:∵一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,
∴两车相向运动,D图象不符合;
∵当6≤x≤10时,S=60x,
∴当x=6时,快车到达目的地,当x=10时,慢车到达目的地,A图象不符合;
又∵S关于x的函数关系式是两车之间的距离关于客车行驶时间的函数关系式,
∴客车用了10小时达到目的地,C图象符合题意.
故选:C.
3.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( )
A.2m B.1.5m C.3m D.3.5m
【解答】解:快者的速度为60÷10=6m/s,
慢者的速度为(60﹣15)÷10=4.5m/s,∴6﹣4.5=1.5,故选:B.
4.有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为( )
A.10厘米 B.13.5厘米 C.14厘米 D.14.5厘米
【解答】答:由表中关系可以得到,弹簧长度y(厘米)与称重x(千克)的关系是一次函数关系,
∴设弹簧长度y(厘米)与称重x(千克)的关系式为y=kx+b,
根据表格中提供的数据得当x=1时,y=4.5;当x=2时,y=5.5;
∴,解得:,∴解析式为y=3.5+x,
当弹簧最长时就是所挂重物最重时,此时x=10,∴y=3.5+10=13.5,
故弹簧最长为13.5厘米.故选:B.
5.某地电话拨号入网有两种收费方式:A计时制:每分0.05元;B包月制:每月50元.此外,每一种上网方式都得加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,你认为采用哪种收费方式较为合算?( )
A.计时制 B.包月制 C.两种一样 D.不确定
【解答】解:根据题意,计时制 y=(0.05+0.02)?60x=4.2x;
包月制 y=50+0.02?60x=50+1.2x;
当x=20时,计时制费用 y=4.2×20=84(元);
包月制费用 y=50+1.2×20=74(元),
所以 一个月内上网的时间为20小时,采用包月制较为合算.
故选:B.
6.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
根据上表解决下面这个实际问题:姚明的身高是226厘米,他的指距为( )
A.26.8厘米 B.26.9厘米 C.27.5厘米 D.27.3厘米
【解答】解:设这个一次函数的解析式是:y=kx+b,
,解得:,
一次函数的解析式是:y=9x﹣20,当y=226时,9x﹣20=226,x=27.3.故选:D.
7.已知:一次函数y=ax+b中的自变量x与函数y的对应值如下表所示:
x
…
﹣1
0
…
y
…
﹣π
1
…
则关于x的方程ax+b=0的解满足( )
A.x<1 B.﹣1<x<0 C.0<x<1 D.x>1
【解答】解:∵x=﹣1时,y=﹣π;x=0时,y=1,
∴﹣1<x<0时,y的值由负到正,∴关于x的方程ax+b=0的解满足﹣1<x<0.
故选:B.
8.当﹣1≤x≤2时,函数y=ax+6满足y<10,则常数a的取值范围是( )
A.﹣4<a<0 B.0<a<2
C.﹣4<a<2且a≠0 D.﹣4<a<2
【解答】解:由题意a≠0
当a<0时,函数y=ax+6为一次函数,它是递减的,
当﹣1≤x≤2时,y<10.
则有当x=﹣1,y=ax+6=﹣a+6<10,
解得:a>﹣4,
故此时:﹣4<a<0;
当a>0时,函数y=ax+6为一次函数,它是递增的,
当x=2,y=ax+6=2a+6<10,解得a<2;
故可得此时0<a<2;
所以﹣4<a<2,且a≠0.
故选:C.
9.已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市.如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
①甲车出发时的速度是60千米/时;
②乙车的速度是96千米/时;
③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市时乙车已返回A市2小时20分
钟.其中正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
【解答】解:①甲车提速后的速度为:80÷2×1.5=60(千米/时),故①正确;
②乙车的速度为80×2÷(4﹣2﹣)=96(千米/时),故②正确;
③∵修车用了20分钟,
∴点C的横坐标为4﹣(4﹣2﹣)÷2=,
∴点C的坐标为(,80).
设乙车返回时y与x的函数关系式为y=kx+b,
将点(,80)、(4,0)代入y=kx+b,
,
解得,
∴乙车返回时y与x的函数关系式为y=﹣96x+384,故③正确;
④甲车到达B市的时间为+(260﹣80)÷60=(小时),
∵﹣4=(小时),
∴甲车到达B市时乙车已返回A市小时,故④错误.
综上所述:正确的结论有①②③.
故选:C.
10.如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=﹣2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=,AB=2,则m,n的值分别是( )
A.3,2 B.2,1 C. D.1,
【解答】解:根据题意得:点A的坐标为(﹣n,0),点Q的坐标为(0,n),点B的坐标为(,0),
∵点P是PA与PB的交点,
∴,
解得:,
∴点P的坐标为:(,),
∵AB=2,
∴OA+OB=n+==2,
∴m+2n=4,
∵S四边形PQOB=,
∴S△PAB﹣S△AOQ=×2×﹣n×n=﹣n2=,
解得:n=1,
∴m=2.
故选:B.
二.填空题(共6小题)
11.长方形的长为3cm,宽为2cm,若长增加xcm,则它的面积S(cm2)与x(cm)之间的函数关系式是 S=2x+6 ,它是 一次 函数,它的图象是 直线 .
【解答】解:∵长方形的长为3cm,宽为2cm,长增加xcm,
∴长为:(3+x)cm,
∴它的面积S(cm2)与x(cm)之间的函数关系式是:S=2(3+x)=2x+6.
∴此函数是一次函数,图象是直线,
故答案为:S=2x+6,一次,直线.
12.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系式如图所示,其中BA是线段,且BA∥x轴,AC是射线,若小李12月份上网费用为84元,则他在该月份上网时间是 38 小时.
【解答】解:当x≥30时,设函数关系式为y=kx+b,
则,
解得.
所以y=3x﹣30;
由84=3x﹣30
解得:x=38,所以他在该月份上网时间是38小时.
故答案为:38.
13.已知一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),则a+b= 16 .
【解答】解:∵一次函数y=﹣x+a与y=x+b的图象相交于点(m,8),
∴﹣m+a=8①,m+b=8②,
①+②得:a+b=16.
故填16.
14.孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,﹣1),则b的正确值是 ﹣13 .
【解答】解:依题意得:2=﹣k+6,k=4;
又∵﹣1=3×4+b,
∴b=﹣13,
故答案为:﹣13.
15.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有 40 米.
【解答】解:设乙的速度为x米/秒,根据图象得到360+180×15=180x,
解得x=17,
乙到达终点所用时间为:3400÷17=200s,
则此时甲离终点的距离为:3400﹣(360+15×200)=40m.
故答案为:40.
16.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An+1作x轴的垂线交一次函数的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的坐标是 (n+,) .
【解答】解:由已知得A1,A2,A3,…的坐标为:(1,0),(2,0),(3,0),…,
又得作x轴的垂线交一次函数y=x的图象于点B1,B2,B3,…的坐标分别为(1,),(2,1),(3,),….
由此可推出An,Bn,An+1,Bn+1四点的坐标为,(n,0),(n,),(n+1,0),(n+1,).
所以得直线AnBn+1和An+1Bn的直线方程分别为:
y﹣0=(x﹣n)+0,
y﹣0=(x﹣n﹣1)+0,
即,
解得:
,
故答案为:(n+,).
三.解答题(共7小题)
17.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1).
(1)求一次函数的解析式;
(2)请直接写出不等式组﹣1<kx+b<2x的解集.
【解答】解:(1)∵点A(m,2)在正比例函数y=2x的图象上,
∴2=2m,解得:m=1,
∴点A的坐标为(1,2).
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
,解得:,
∴一次函数的解析式为y=x+1.
(2)∵在y=x+1中,1>0,
∴y值随x值的增大而增大,
∴不等式﹣1<x+1的解集为x>﹣2.
观察函数图象可知,当x>1时,一次函数y=x+1的图象在正比例函数y=2x的图象的下方,
∴不等式组﹣1<x+1<2x的解集为x>1.
18.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=﹣1交于点D,C为直线y轴的交点.
(1)求直线AB的解析式;
(2)求S△ADC.
【解答】解:(1)设直线AB的解析式为y=kx+b,
把A(0,2),B(3,0)分别代入得,解得,
所以直线AB的解析式为y=﹣x+2;
(2)当x=0时,y=﹣1=﹣1,则C(0,﹣1),
解方程组得,则D(2,),
所以S△ADC=×(2+1)×2=3.
19.某厂准备购买A、B、C三种配件共1000件,要求购买时C配件的件数是A配件件数的4倍,B配件不超过400件,且每种配件必须买,三种配件的价格如下表:
配件
A
B
C
价格(元/件)
30
50
80
假设购买A配件x(件),买全配件所需的总费用为y(元).
(1)求y与x之间的函数关系式;
(2)要使买全配件所需的总费用最少,三种配件应各买多少件?所需总费用最少多少元?
【解答】解:(1)设购买A配件x(件),则C配件购买4x件,B配件购买(1000﹣5x)件,由题意,得
y=30x+80×4x+50(1000﹣5x),
y=100x+50000.
答:y与x之间的函数关系式为y=100x+50000;
(2)∵B配件不超过400件,
∴1000﹣5x≤400,
∴x≥120.
∵y=100x+50000,
∴k=100>0,
∴x=120时,y最大=62000.
∴B配件为:1000﹣120×5=400,
C配件为:120×4=480.
答:购买A配件120件,B配件400件,C配件480件时,总费用最少为62000元.
20.小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.下图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.
(1)分别求出AB段和BC段图象所在直线的解析式.
(2)到达旅游目的地后,司机说:“今日改走高速公路后比往日全走普通公路省油6升”,求此时油箱内的余油量.(假设走高速公路和走普通公路的路程一样)
(3)已知出租车在高速公路上匀速行驶的速度是100千米/小时,求出租车在高速公路上行驶的时间.
【解答】解(1)设AB段所在直线的解析式为Q=k1s+b1,
则据图象可得,解得.
∴AB段所在直线的解析式为.
又设BC图象所在直线的解析为Q=k2s+b2,
同样可得 解得.
∴BC段所在直线的解析式为.
(2)据题意可得,解得s=350(千米).
∴当s=350时,.
(3)出租车在高速公路上行驶的时间为:(350﹣50)÷100=3(小时).
21.某项工程若由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲乙两人合作,则需12天完成.
(1)甲乙两队单独完成各需多少天?
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)与施工时间x(天)的函数关系式;
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
【解答】解:(1)设乙单独完成需a天,则甲单独完成需1.5a天,
根据题意列:+=,
解得,a=20,
经检验:a=20是所列方程根,且符合题意,
所以1.5a=30,
答:甲、乙两队单独完成分别需30天,20天;
(2)设甲乙合作完成余下部分所需时间为w天,列:++=1,
解得,w=﹣x+12,
∴y=x+(1+2.5)(﹣x+12)=﹣x+42;
(3)由题可得15≤x﹣x+12≤18,
解得,5≤x≤10,
∵﹣<0,
∴y随x的增大而减小,
∴当x=10时,y最小=﹣×10+42=38,
此时,甲先施工10天,再甲乙合作8天,费用最低为38万元.
22.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:
(1)自行车队行驶的速度是 24 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
【解答】解:(1)由题意得
自行车队行驶的速度是:72÷3=24km/h.
故答案为:24;
(2)由题意得
邮政车的速度为:24×2.5=60km/h.
设邮政车出发a小时两车相遇,由题意得
24(a+1)=60a,
解得:a=.
答:邮政车出发小时与自行车队首次相遇;
(3)由题意,得
邮政车到达丙地的时间为:135÷60=,
∴邮政车从丙地出发的时间为:,
∴B(,135),C(7.5,0).
自行车队到达丙地的时间为:135÷24+0.5=+0.5=,
∴D(,135).
设BC的解析式为y1=k1x+b1,由题意得
,
∴,
∴y1=﹣60x+450,
设ED的解析式为y2=k2x+b2,由题意得
,
解得:,
∴y2=24x﹣12.
当y1=y2时,
﹣60x+450=24x﹣12,
解得:x=5.5.
y1=﹣60×5.5+450=120.
答:邮政车在返程途中与自行车队再次相遇时的地点距离甲地120km.
23.规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k?b≠0,且|k|≠|b|)为互助一次函数,例如和就是互助一次函数.如图,一次函数y=kx+b和它的互助一次函数的图象l1,l2交于P点,l1,l2与x轴,y轴分别交于A,B点和C,D点.
(1)如图(1),当k=﹣1,b=3时,
①直接写出P点坐标:P (1,2) ;
②Q是射线CP上一点(与C点不重合),其横坐标为m,求四边形OCQB的面积S与m之间的函数关系式,并求当△BCQ与△ACP面积相等时m的值;
(2)如图(2),已知点M(﹣1,2),N(﹣2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化?若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时的P点坐标.
【解答】解:(1)①∵一次函数y=kx+b和它的互助一次函数的图象交于P点,
k=﹣1,b=3时,
∴,
解得:,
∴P(1,2);
故答案为:(1,2);
②如图(1),连接OQ,
∵y=﹣x+3与y=3x﹣1的图象l1,l2与x轴,y轴分别交于A,B点和C,D点.
∴A(3,0),B(0,3),C(,0),D(0,﹣1).
∵Q(m,3m﹣1),(),
∴S=S△OBQ+S△OCQ==.
∴S△BCQ=S﹣S△BOC==,
而S△ACP==,
由S△BCQ=S△ACP,得 =,
解得m=;
(2)由,
解得 ,即P(1,k+b),
∴随着k,b值的变化,点P在直线x=1上运动,MP+NP的值随之发生变化.
如图(2),作点N(﹣2,0)关于直线x=1的对称点N′(4,0),
连接MN′交直线x=1于点P,则此时MP+NP取得最小值.
设直线MN′的解析式为y=cx+d,依题意,
解得 ,
∴直线MN′的解析式为.
令x=1,则,
∴P(1,),
即 使MP+NP取最小值时的P点坐标为(1,).
