2018-2019学年江苏省镇江市京口区江南中学九年级(下)开学数学试卷解析版
文档属性
| 名称 | 2018-2019学年江苏省镇江市京口区江南中学九年级(下)开学数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 103.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-01 11:48:45 | ||
图片预览



文档简介
2018-2019学年江苏省镇江市京口区江南中学九年级(下)开学数学试卷
一、选择题(每小题4分,共20分)
1.(4分)若=,则的值为( )
A.1 B. C. D.
2.(4分)已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A. B. C. D.
3.(4分)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
4.(4分)过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
5.(4分)如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
二、填空题(毎空3分,共24分)
6.(3分)如果在比例尺为1:2000000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
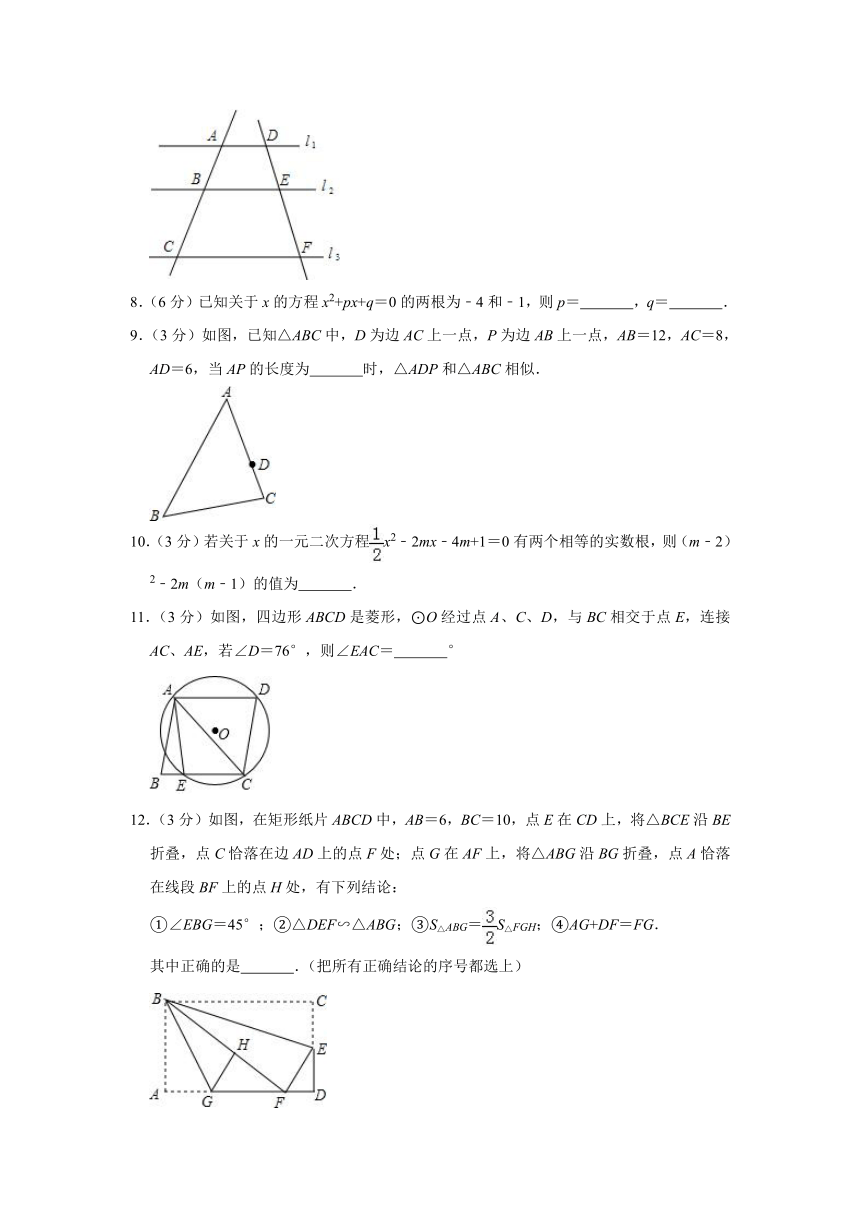
7.(3分)如图,已知:l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
8.(6分)已知关于x的方程x2+px+q=0的两根为﹣4和﹣1,则p= ,q= .
9.(3分)如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
10.(3分)若关于x的一元二次方程x2﹣2mx﹣4m+1=0有两个相等的实数根,则(m﹣2)2﹣2m(m﹣1)的值为 .
11.(3分)如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE,若∠D=76°,则∠EAC= °
12.(3分)如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.
其中正确的是 .(把所有正确结论的序号都选上)
三、解答题(共56分)
13.(12分)计算
(1)(﹣3)2﹣+(﹣2)0﹣()﹣2
(2)解方程:=+1
14.(8分)一个不透明的口袋中有三个完全相同的小球,把他们分别标号为1,2,3.随机摸取一个小球然后放回,再随机摸出一个小球.用列表或画树状图的方法,求两次取出的小球标号相同的概率.
15.(8分)某公司共25名员工,下表是他们月收入的资料.
月收入/元
45000
18000
10000
5500
4800
3400
3000
2200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元.
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
16.(8分)如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
17.(10分)如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
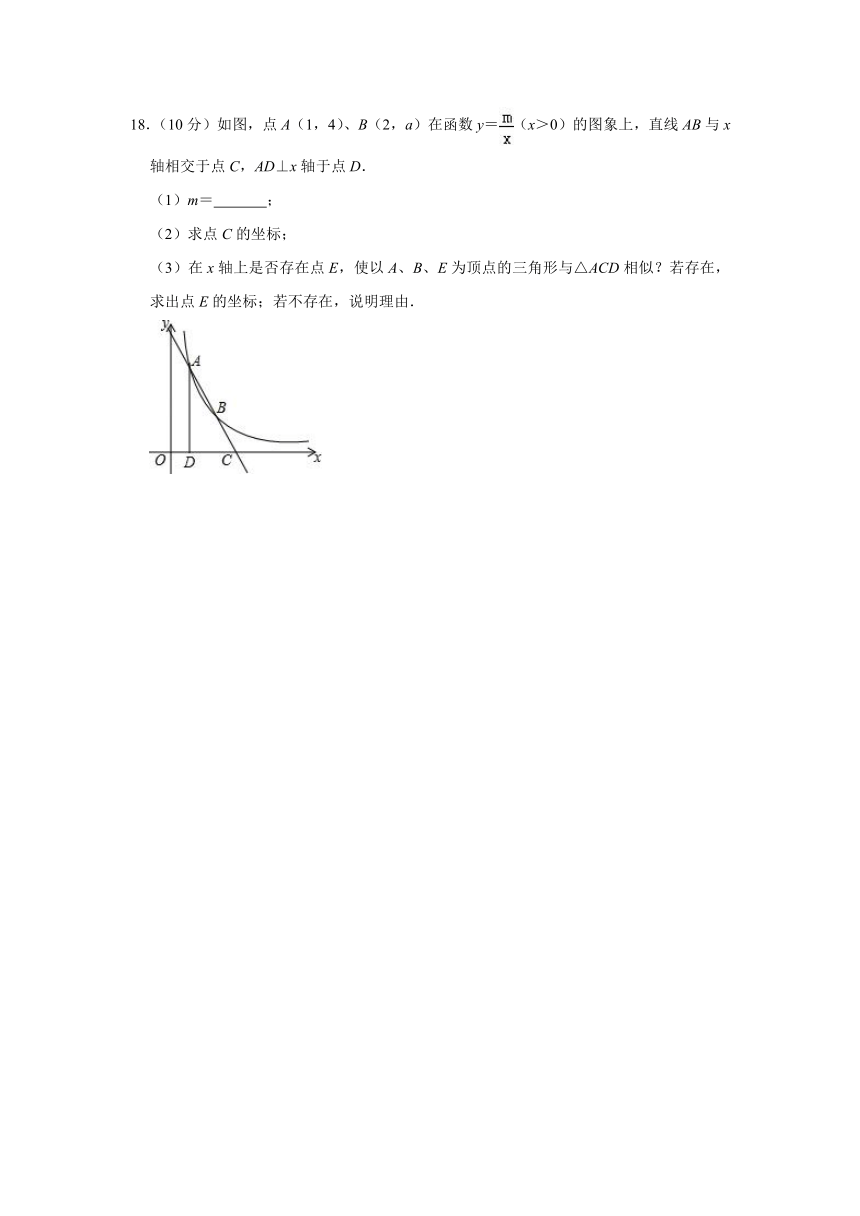
18.(10分)如图,点A(1,4)、B(2,a)在函数y=(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
2018-2019学年江苏省镇江市京口区江南中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题4分,共20分)
1.【解答】解:∵=,
∴==.
故选:D.
2.【解答】解:由于P为线段AB=4的黄金分割点,
且AP是较长线段;
则AP=4×=2﹣2.
故选:A.
3.【解答】解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
D、无法得到△ABP∽△ACB,故此选项正确.
故选:D.
4.【解答】解:已知A(2,2),B(6,2),C(4,5),
∴AB的垂直平分线是x==4,
设直线BC的解析式为y=kx+b,
把B(6,2),C(4,5)代入上式得
,
解得,
∴y=﹣x+11,
设BC的垂直平分线为y=x+m,
把线段BC的中点坐标(5,)代入得m=,
∴BC的垂直平分线是y=x+,
当x=4时,y=,
∴过A、B、C三点的圆的圆心坐标为(4,).
故选:A.
5.【解答】解:如图,∵△ABC和△ADE均为等边三角形,
∴∠B=∠BAC=60°,
∴∠BAD+∠ADB=120°,∠ADB+∠FDC=120°
∴∠BAD=∠FDC
又∵∠B=∠C=60°,∴
∴△ABD~△CDF,
∴AB:BD=CD:CF,
即9:3=(9﹣3):CF,
∴CF=2.
故选:B.
二、填空题(毎空3分,共24分)
6.【解答】解:根据题意,3.4÷=1700000厘米=17千米.
即实际距离是17千米.
故答案为:17.
7.【解答】解:∵:l1∥l2∥l3,
∴=,
∵AB=6,DE=5,EF=7.5,
∴BC=9,
∴AC=AB+BC=15,
故答案为:15.
8.【解答】解:∵关于x的方程x2+px+q=0的两根为﹣4和﹣1,
∴﹣4+(﹣1)=﹣p,(﹣4)×(﹣1)=q,
∴p=5,q=4.
故答案为:5;4.
9.【解答】解:当△ADP∽△ACB时,
∴=,
∴=,
解得:AP=9,
当△ADP∽△ABC时,
∴=,
∴=,
解得:AP=4,
∴当AP的长度为4或9时,△ADP和△ABC相似.
故答案为:4或9.
10.【解答】解:由题意可知:△=4m2﹣2(1﹣4m)=4m2+8m﹣2=0,
∴m2+2m=
∴(m﹣2)2﹣2m(m﹣1)
=﹣m2﹣2m+4
=+4
=
故答案为:
11.【解答】解:∵四边形ABCD是菱形,∠D=76°,
∴∠ACB=∠DCB=(180°﹣∠D)=52°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=76°,
∴∠EAC=∠AEB﹣∠ACE=24°,
故答案为:24.
12.【解答】解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,
∴AF==8,
∴DF=AD﹣AF=10﹣8=2,
设EF=x,则CE=x,DE=CD﹣CE=6﹣x,
在Rt△DEF中,∵DE2+DF2=EF2,
∴(6﹣x)2+22=x2,解得x=,
∴ED=,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=∠ABC=45°,所以①正确;
HF=BF﹣BH=10﹣6=4,
设AG=y,则GH=y,GF=8﹣y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8﹣y)2,解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D,==,=,
∴≠,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG=?6?3=9,S△FGH=?GH?HF=×3×4=6,
∴S△ABG=S△FGH,所以③正确;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
故答案为①③④.
三、解答题(共56分)
13.【解答】解:(1)原式=9﹣4+1﹣9
=﹣3;
(2)方程两边都乘以3(x+1),得:3x=2x+3x+3,
解得:x=,
检验:当x=﹣时,3(x+1)≠0,
所以分式方程的解为x=﹣.
14.【解答】解:画树状图得:
则共有9种等可能的结果,两次摸出的小球标号相同时的情况有3种,
所以两次取出的小球标号相同的概率为.
15.【解答】解:(1)共有25个员工,中位数是第13个数,
则中位数是3400元;
3000出现了11次,出现的次数最多,则众数是3000.
故答案为3400;3000;
(2)用中位数或众数来描述更为恰当.理由:
平均数受极端值45000元的影响,只有3个人的工资达到了6276元,不恰当;
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB;
(2)由(1)知△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=.
17.【解答】解:(1)如图,连接OB,
∵PA,PB是⊙O的切线,
∴PO平分∠APC;
(2)∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°﹣∠C=90°﹣30°=60°,
∵PO平分∠APC,
∴∠OPC=∠APC==30°,
∴∠POB=90°﹣∠OPC=90°﹣30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP﹣∠OBD=90°﹣60°=30°,
∴∠DBP=∠C,
∴DB∥AC.
18.【解答】解:(1)∵点A(1,4)在反比例函数y=(x>0)的图象上,
∴m=1×4=4,
故答案为:4.
(2)∵点B(2,a)在反比例函数y=的图象上,
∴a==2,
∴B(2,2).
设过点A、B的直线的解析式为y=kx+b,
∴,解得:,
∴过点A、B的直线的解析式为y=﹣2x+6.
当y=0时,有﹣2x+6=0,
解得:x=3,
∴点C的坐标为(3,0).
(3)假设存在,设点E的坐标为(n,0).
①当∠ABE=90°时(如图1所示),∵A(1,4),B(2,2),C(3,0),
∴B是AC的中点,
∴EB垂直平分AC,EA=EC=3﹣n.
由勾股定理得:AD2+DE2=AE2,即42+(1﹣n)2=(3﹣n)2,
解得:n=﹣2,
此时点E的坐标为(﹣2,0);
②当∠BAE=90°时,∠ABE>∠ACD,
故△EBA与△ACD不可能相似;
③当∠AEB=90°时,∵A(1,4),B(2,2),
∴AB=,2>,
∴以AB为直径作圆与x轴无交点(如图3),
∴不存在∠AEB=90°.
综上可知:在x轴上存在点E,使以A、B、E为顶点的三角形与△ACD相似,点E的坐标为(﹣2,0).
一、选择题(每小题4分,共20分)
1.(4分)若=,则的值为( )
A.1 B. C. D.
2.(4分)已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A. B. C. D.
3.(4分)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
4.(4分)过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
5.(4分)如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
二、填空题(毎空3分,共24分)
6.(3分)如果在比例尺为1:2000000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
7.(3分)如图,已知:l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
8.(6分)已知关于x的方程x2+px+q=0的两根为﹣4和﹣1,则p= ,q= .
9.(3分)如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
10.(3分)若关于x的一元二次方程x2﹣2mx﹣4m+1=0有两个相等的实数根,则(m﹣2)2﹣2m(m﹣1)的值为 .
11.(3分)如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE,若∠D=76°,则∠EAC= °
12.(3分)如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.
其中正确的是 .(把所有正确结论的序号都选上)
三、解答题(共56分)
13.(12分)计算
(1)(﹣3)2﹣+(﹣2)0﹣()﹣2
(2)解方程:=+1
14.(8分)一个不透明的口袋中有三个完全相同的小球,把他们分别标号为1,2,3.随机摸取一个小球然后放回,再随机摸出一个小球.用列表或画树状图的方法,求两次取出的小球标号相同的概率.
15.(8分)某公司共25名员工,下表是他们月收入的资料.
月收入/元
45000
18000
10000
5500
4800
3400
3000
2200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元.
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
16.(8分)如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
17.(10分)如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
18.(10分)如图,点A(1,4)、B(2,a)在函数y=(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
2018-2019学年江苏省镇江市京口区江南中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题4分,共20分)
1.【解答】解:∵=,
∴==.
故选:D.
2.【解答】解:由于P为线段AB=4的黄金分割点,
且AP是较长线段;
则AP=4×=2﹣2.
故选:A.
3.【解答】解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
D、无法得到△ABP∽△ACB,故此选项正确.
故选:D.
4.【解答】解:已知A(2,2),B(6,2),C(4,5),
∴AB的垂直平分线是x==4,
设直线BC的解析式为y=kx+b,
把B(6,2),C(4,5)代入上式得
,
解得,
∴y=﹣x+11,
设BC的垂直平分线为y=x+m,
把线段BC的中点坐标(5,)代入得m=,
∴BC的垂直平分线是y=x+,
当x=4时,y=,
∴过A、B、C三点的圆的圆心坐标为(4,).
故选:A.
5.【解答】解:如图,∵△ABC和△ADE均为等边三角形,
∴∠B=∠BAC=60°,
∴∠BAD+∠ADB=120°,∠ADB+∠FDC=120°
∴∠BAD=∠FDC
又∵∠B=∠C=60°,∴
∴△ABD~△CDF,
∴AB:BD=CD:CF,
即9:3=(9﹣3):CF,
∴CF=2.
故选:B.
二、填空题(毎空3分,共24分)
6.【解答】解:根据题意,3.4÷=1700000厘米=17千米.
即实际距离是17千米.
故答案为:17.
7.【解答】解:∵:l1∥l2∥l3,
∴=,
∵AB=6,DE=5,EF=7.5,
∴BC=9,
∴AC=AB+BC=15,
故答案为:15.
8.【解答】解:∵关于x的方程x2+px+q=0的两根为﹣4和﹣1,
∴﹣4+(﹣1)=﹣p,(﹣4)×(﹣1)=q,
∴p=5,q=4.
故答案为:5;4.
9.【解答】解:当△ADP∽△ACB时,
∴=,
∴=,
解得:AP=9,
当△ADP∽△ABC时,
∴=,
∴=,
解得:AP=4,
∴当AP的长度为4或9时,△ADP和△ABC相似.
故答案为:4或9.
10.【解答】解:由题意可知:△=4m2﹣2(1﹣4m)=4m2+8m﹣2=0,
∴m2+2m=
∴(m﹣2)2﹣2m(m﹣1)
=﹣m2﹣2m+4
=+4
=
故答案为:
11.【解答】解:∵四边形ABCD是菱形,∠D=76°,
∴∠ACB=∠DCB=(180°﹣∠D)=52°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=76°,
∴∠EAC=∠AEB﹣∠ACE=24°,
故答案为:24.
12.【解答】解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,
∴AF==8,
∴DF=AD﹣AF=10﹣8=2,
设EF=x,则CE=x,DE=CD﹣CE=6﹣x,
在Rt△DEF中,∵DE2+DF2=EF2,
∴(6﹣x)2+22=x2,解得x=,
∴ED=,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=∠ABC=45°,所以①正确;
HF=BF﹣BH=10﹣6=4,
设AG=y,则GH=y,GF=8﹣y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8﹣y)2,解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D,==,=,
∴≠,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG=?6?3=9,S△FGH=?GH?HF=×3×4=6,
∴S△ABG=S△FGH,所以③正确;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
故答案为①③④.
三、解答题(共56分)
13.【解答】解:(1)原式=9﹣4+1﹣9
=﹣3;
(2)方程两边都乘以3(x+1),得:3x=2x+3x+3,
解得:x=,
检验:当x=﹣时,3(x+1)≠0,
所以分式方程的解为x=﹣.
14.【解答】解:画树状图得:
则共有9种等可能的结果,两次摸出的小球标号相同时的情况有3种,
所以两次取出的小球标号相同的概率为.
15.【解答】解:(1)共有25个员工,中位数是第13个数,
则中位数是3400元;
3000出现了11次,出现的次数最多,则众数是3000.
故答案为3400;3000;
(2)用中位数或众数来描述更为恰当.理由:
平均数受极端值45000元的影响,只有3个人的工资达到了6276元,不恰当;
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB;
(2)由(1)知△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=.
17.【解答】解:(1)如图,连接OB,
∵PA,PB是⊙O的切线,
∴PO平分∠APC;
(2)∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°﹣∠C=90°﹣30°=60°,
∵PO平分∠APC,
∴∠OPC=∠APC==30°,
∴∠POB=90°﹣∠OPC=90°﹣30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP﹣∠OBD=90°﹣60°=30°,
∴∠DBP=∠C,
∴DB∥AC.
18.【解答】解:(1)∵点A(1,4)在反比例函数y=(x>0)的图象上,
∴m=1×4=4,
故答案为:4.
(2)∵点B(2,a)在反比例函数y=的图象上,
∴a==2,
∴B(2,2).
设过点A、B的直线的解析式为y=kx+b,
∴,解得:,
∴过点A、B的直线的解析式为y=﹣2x+6.
当y=0时,有﹣2x+6=0,
解得:x=3,
∴点C的坐标为(3,0).
(3)假设存在,设点E的坐标为(n,0).
①当∠ABE=90°时(如图1所示),∵A(1,4),B(2,2),C(3,0),
∴B是AC的中点,
∴EB垂直平分AC,EA=EC=3﹣n.
由勾股定理得:AD2+DE2=AE2,即42+(1﹣n)2=(3﹣n)2,
解得:n=﹣2,
此时点E的坐标为(﹣2,0);
②当∠BAE=90°时,∠ABE>∠ACD,
故△EBA与△ACD不可能相似;
③当∠AEB=90°时,∵A(1,4),B(2,2),
∴AB=,2>,
∴以AB为直径作圆与x轴无交点(如图3),
∴不存在∠AEB=90°.
综上可知:在x轴上存在点E,使以A、B、E为顶点的三角形与△ACD相似,点E的坐标为(﹣2,0).
同课章节目录
