2018-2019学年江苏省宿迁市沭阳县高一(下)期中数学试卷解析版
文档属性
| 名称 | 2018-2019学年江苏省宿迁市沭阳县高一(下)期中数学试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-02 00:00:00 | ||
图片预览




文档简介
2018-2019学年江苏省宿迁市沭阳县高一(下)期中数学试卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)计算sin13°cos17°+cos13°sin17°的值为( )
A. B. C.﹣ D.﹣
2.(5分)在△ABC中,角A,B,C的对边边长分别为a,b,c,若a=2,b=3,C=120°,则其面积等于( )
A. B. C. D.
3.(5分)已知△ABC中,角A、B、C的对边分别为a、b、c,若A:B:C=1:1:4,则a:b:c=( )
A.1:1: B.2:2: C.1:1:2 D.1:1:4
4.(5分)下列命题正确的是( )
A.两两相交且不共点的三条直线确定一个平面
B.四边形确定一个平面
C.经过一条直线和一个点确定一个平面
D.经过三点确定一个平面
5.(5分)函数y=2cos2(x+)﹣1是( )
A.最小正周期为π的偶函数
B.最小正周期为的奇函数
C.最小正周期为π的奇函数
D.最小正周期为的偶函数
6.(5分)在△ABC中,a2=b2+c2﹣bc,则角A为( )
A.30° B.150° C.120° D.60°
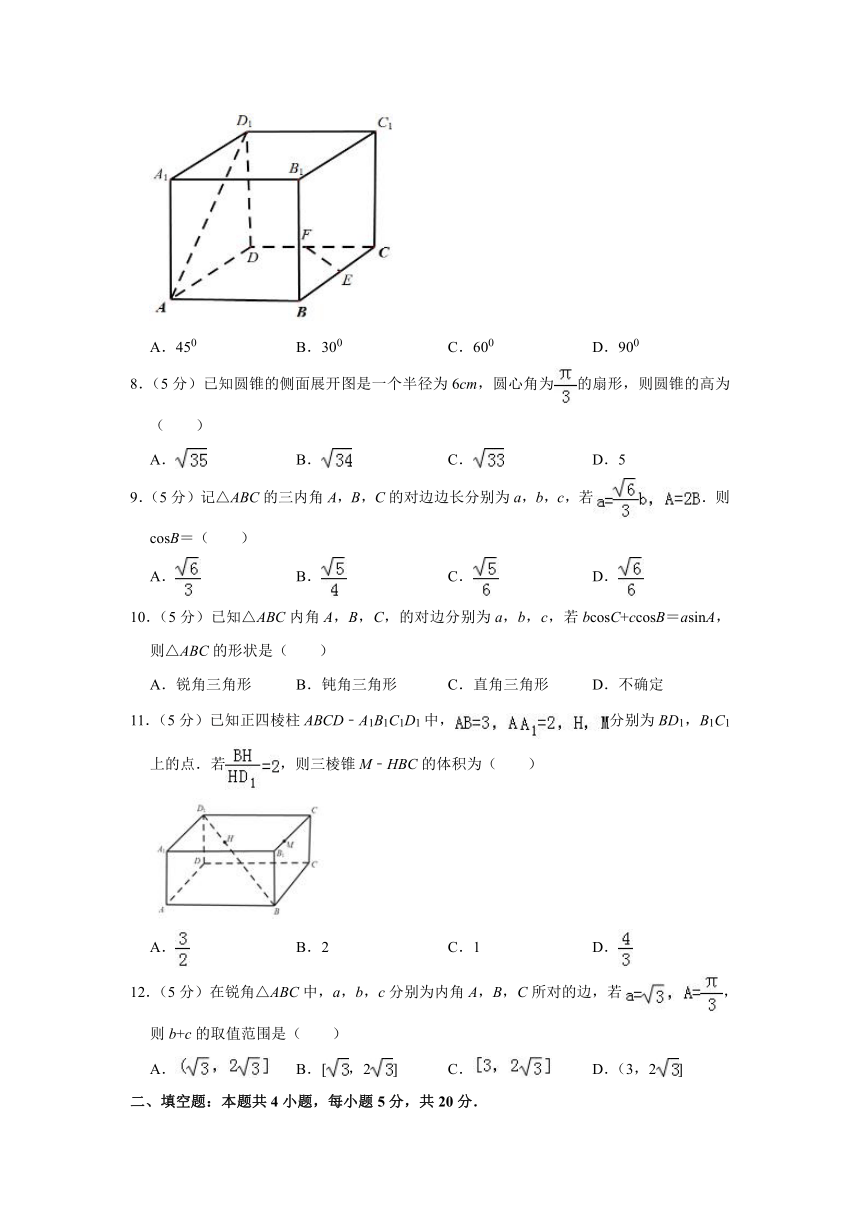
7.(5分)如图,在正方体ABCD﹣A1B1C1D1中,AA1=1,E,F分别是BC,DC中点,则异面直线AD1与EF所成角大小为( )
A.450 B.300 C.600 D.900
8.(5分)已知圆锥的侧面展开图是一个半径为6cm,圆心角为的扇形,则圆锥的高为( )
A. B. C. D.5
9.(5分)记△ABC的三内角A,B,C的对边边长分别为a,b,c,若.则cosB=( )
A. B. C. D.
10.(5分)已知△ABC内角A,B,C,的对边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不确定
11.(5分)已知正四棱柱ABCD﹣A1B1C1D1中,分别为BD1,B1C1上的点.若,则三棱锥M﹣HBC的体积为( )
A. B.2 C.1 D.
12.(5分)在锐角△ABC中,a,b,c分别为内角A,B,C所对的边,若,则b+c的取值范围是( )
A. B.[,2] C. D.(3,2]
二、填空题:本题共4小题,每小题5分,共20分.
13.(5分)已知sinα﹣2cosα=0,则tan2α= .
14.(5分)△ABC中,,则BC边上中线AD的长为 .
15.(5分)已知关于x的方程cos2x﹣2cosx=m﹣1有实数解,则实数m的取值范围是 .
16.(5分)已知OA,OB,OC三条线段两两垂直,长分别是2,x,5,且O,A,B,C4个点都在同一个球面上,这个球的表面积为38π,则x的值 .
三、解答题:本大题共6小题,共计70分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
17.(10分)已知三棱锥P﹣ABC中,AB⊥AC,AB⊥AP.若平面α分别与棱PA、PB、BC、AC相交于点E、F、G、H,且PC∥平面α,求证:
(1)AB⊥EH;
(2)FG∥面PAC.
18.(12分)在△ABC中,已知AB=2,AC=3,BC=.
(1)求角A的大小;
(2)求cos(B﹣C)的值.
19.(12分)如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC.
(1)证明:平面PAC⊥平面PBC;
(2)设PA=3,,求点A到平面PBC的距离.
20.(12分)已知,若,,求sin(α﹣β)的值.
21.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且cosA=,tan(B﹣A)=.
(1)求tanB的值;
(2)若c=13,求△ABC的面积.
22.(12分)某小区内有一块以O为圆心半径为20米的圆形区域.广场,为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形OAB区域,其中两个端点A,B分别在圆周上;观众席为梯形ABQP内且在圆O外的区域,其中AP=AB=BQ,∠PAB=∠QBA=120°,且AB,PQ在点O的同侧.为保证视听效果,要求观众席内每一个观众到舞台O处的距离都不超过60米.设.
(1)求AB的长(用α表示);
(2)对于任意α,上述设计方案是否均能符合要求?
2018-2019学年江苏省宿迁市沭阳县高一(下)期中数学试卷
参考答案与试题解析
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:sin17°cos13°+cos17°sin13°
=sin(17°+13°)
=sin30°
=.
故选:B.
2.【解答】解:△ABC中,角A,B,C的对边边长分别为a,b,c,
若a=2,b=3,C=120°,
则S△ABC=ab×sin120°=×2×3×=,
故选:C.
3.【解答】解:△ABC中,A:B:C=1:1:4,
所以三个内角分别为30°,30°,120°;
则a:b:c=sinA:sinB:sinC
=::
=1:1:.
故选:A.
4.【解答】解:对于A,两两相交且不共点的三条直线确定一个平面,
如三角形所在的三边确定一个平面,∴A正确;
对于B,经过一条直线和一个点不一定能确定一个平面,
如点在直线上时,∴B错误;
对于C,经过不在同一条直线上的三点确定一个平面,∴C错误;
对于D,空间四边形不能确定一个平面,∴D错误.
故选:A.
5.【解答】解:由题意得,y=2cos2(x+)﹣1=cos2(x+)=cos(2x+)=﹣sin2x,
∴函数的最小正周期是π,且是奇函数,
故选:C.
6.【解答】解:∵在△ABC中,a2=b2+c2﹣bc,即b2+c2﹣a2=bc,
∴cosA==,
则A=60°,
故选:D.
7.【解答】解:取CC1的中点G,连EG,BC1,
易得EF∥BC1∥AD1,
所以异面直线AD1与EF所成角是∠FEG或其补角,
在三角形EFG中,EF=EG=FG,∴∠FEG=60°.
故选:C.
8.【解答】解:扇形的弧长等于6×=2π,
所以圆锥的底面周长为2π,底面半径为1,
∴圆锥的高为=.
故选:A.
9.【解答】解:∵△ABC中,,
∴根据正弦定理得:sinA=sinB=2sinBcosB,
∵sinB>0,
∴cosB=.
故选:D.
10.【解答】解:△ABC中,∵bcosC+ccosB=asinA,
∴由正弦定理得:sinBcosC+sinCcosB=sin2A,
即sin(B+C)=sin(π﹣A)=sinA=sin2A,又sinA>0,
∴sinA=1,A∈(0,π),
∴A=.
∴△ABC的形状是直角三角形,
故选:C.
11.【解答】解:∵,D1C⊥平面BCC1B1,
∴H到平面BCC1B1的距离h=D1C=2,
又S△BCM==3,
∴VM﹣BCH=VH﹣BCM==2.
故选:B.
12.【解答】解:∵由正弦定理可得:==2,
∴b+c
=2sinB+2sinC
=2sinB+2sin(﹣B)
=2sinB+2(cosB+sinB)
=3sinB+cosB
=2sin(B+),
∵B,C为锐角,B+C=,
∴B∈(,),可得:B+∈(,),
∴sin(B+)∈(,1],
∴b+c=2sin(B+)∈(3,2],
故选:D.
二、填空题:本题共4小题,每小题5分,共20分.
13.【解答】解:∵sinα﹣2cosα=0,可得:sina=2cosa,即tanα=2,
∴tan2α===﹣.
故答案为:﹣.
14.【解答】解:∵,
∴由余弦定理可得:BC2=AB2+AC2﹣2AB?AC?cosA=16+4﹣2×=16,解得:BC=4,
∴BD=2,
∴在△ABC中,可得:cosB===,
∴在△ABD中,由余弦定理可得:AD2=AB2+BD2﹣2AB?BD?cosB=16+4﹣2×4×2×=6,
∴解得:AD=.
故答案为:.
15.【解答】解:设f(x)=cos2x﹣2cosx=2cos2x﹣2cosx﹣1=2(cosx﹣)2﹣,
又cosx∈[﹣1,1],
所以﹣≤f(x)≤3,
又关于x的方程cos2x﹣2cosx=m﹣1有实数解,
所以﹣≤m﹣1≤3,
即≤m≤4,
故答案为:[﹣].
16.【解答】解:把三棱锥O﹣ABC补形为长方体,则长方体的对角线长为.
∴三棱锥O﹣ABC的外接球的半径为R=.
由题意,,即x=3.
故答案为:3.
三、解答题:本大题共6小题,共计70分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
17.【解答】证明:(1)∵AB⊥AC,AB⊥AP.
又AC?平面PAC,AP?平面PAC,AC∩AP=A,
∴AB⊥平面PAC,…3分
又EH?面PAC,∴AB⊥EH.…4分
(2)∵PC∥平面α,平面PAC∩平面α=FG,
PC?平面PAC,∴PC∥FG,…7分
又PC?面PAC,FG?面PAC
∴FG∥面PAC.…10分
18.【解答】解:(1)∵AB=2,AC=3,BC=.
∴由余弦定理可得:cosA===,…2分
∵A∈(0,π),
∴A=…5分
(2)由正弦定理:,可得sinC===.
∵AB<BC,
∴C<A,即0,可得:cosC===,…8分
∴sin2C=2sinCcosC=2×=,cos2C=2cos2C﹣1=2×﹣1=,…11分
∵A+B+C=π,A=,可得:B=﹣C,
∴cos(B﹣C)=cos(﹣2C)=coscos2C+sinsin2C=(﹣)×+×=…14分
19.【解答】(1)证明:∵AB是⊙O的直径,点C是⊙O上的动点,
∴∠ACB=90°,即BC⊥AC.………………………2分
又∵PA垂直于⊙O所在的平面ABC,BC?平面⊙O,
∴PA⊥BC………………………………………………4分
又PA∩AC=A,
∴BC⊥平面PAC.
又BC?平面PBC,
∴平面PAC⊥平面PBC.………………………6分
(2)解:由(1)知平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,
过A点作PC的垂线,垂足为D,显然AD⊥平面PBC,
即AD为三棱锥A﹣PBC的高…10分
在Rt△PAC中,,所以,
由AD×PC=PA×AC,得
即点A到平面PCB的距离为,
三棱锥点A到平面PBC的距离:…12分
20.【解答】解:由,得,…2分
由,得;…4分
,得…6分
所以…9分
==…12分
21.【解答】解:(1)在△ABC中,由cosA=,得A为锐角,所以sinA=,
所以tanA==,
所以tanB=tan[(B﹣A)+A]===3;
(2)在三角形ABC中,由tanB=3,
所以sinB=,cosB=,
由sinC=sin(A+B)=sinAcosB+cosAsinB=,
由正弦定理=,得b===15,
所以△ABC的面积S=bcsinA=×15×13×=78.
22.【解答】解:(1)过点O作OH垂直于AB,垂足为H.
在直角三角形OHA中,OA=20,∠OAH=α,
所以AH=20cosα,因此AB=2AH=40cosα…3分
(2)由图可知,点P处的观众离点O最远…5分
在三角形OAP中,由余弦定理可知
=
=
=…9分
因为,所以当,即时,
(OP2)max=800+1600,
又(OP2)max=800+1600<3600
所以(OP)max<60…11分
所以观众席内每一个观众到舞台O处的距离都不超过60米.
故对于任意α,上述设计方案均能符合要求…12分
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)计算sin13°cos17°+cos13°sin17°的值为( )
A. B. C.﹣ D.﹣
2.(5分)在△ABC中,角A,B,C的对边边长分别为a,b,c,若a=2,b=3,C=120°,则其面积等于( )
A. B. C. D.
3.(5分)已知△ABC中,角A、B、C的对边分别为a、b、c,若A:B:C=1:1:4,则a:b:c=( )
A.1:1: B.2:2: C.1:1:2 D.1:1:4
4.(5分)下列命题正确的是( )
A.两两相交且不共点的三条直线确定一个平面
B.四边形确定一个平面
C.经过一条直线和一个点确定一个平面
D.经过三点确定一个平面
5.(5分)函数y=2cos2(x+)﹣1是( )
A.最小正周期为π的偶函数
B.最小正周期为的奇函数
C.最小正周期为π的奇函数
D.最小正周期为的偶函数
6.(5分)在△ABC中,a2=b2+c2﹣bc,则角A为( )
A.30° B.150° C.120° D.60°
7.(5分)如图,在正方体ABCD﹣A1B1C1D1中,AA1=1,E,F分别是BC,DC中点,则异面直线AD1与EF所成角大小为( )
A.450 B.300 C.600 D.900
8.(5分)已知圆锥的侧面展开图是一个半径为6cm,圆心角为的扇形,则圆锥的高为( )
A. B. C. D.5
9.(5分)记△ABC的三内角A,B,C的对边边长分别为a,b,c,若.则cosB=( )
A. B. C. D.
10.(5分)已知△ABC内角A,B,C,的对边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不确定
11.(5分)已知正四棱柱ABCD﹣A1B1C1D1中,分别为BD1,B1C1上的点.若,则三棱锥M﹣HBC的体积为( )
A. B.2 C.1 D.
12.(5分)在锐角△ABC中,a,b,c分别为内角A,B,C所对的边,若,则b+c的取值范围是( )
A. B.[,2] C. D.(3,2]
二、填空题:本题共4小题,每小题5分,共20分.
13.(5分)已知sinα﹣2cosα=0,则tan2α= .
14.(5分)△ABC中,,则BC边上中线AD的长为 .
15.(5分)已知关于x的方程cos2x﹣2cosx=m﹣1有实数解,则实数m的取值范围是 .
16.(5分)已知OA,OB,OC三条线段两两垂直,长分别是2,x,5,且O,A,B,C4个点都在同一个球面上,这个球的表面积为38π,则x的值 .
三、解答题:本大题共6小题,共计70分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
17.(10分)已知三棱锥P﹣ABC中,AB⊥AC,AB⊥AP.若平面α分别与棱PA、PB、BC、AC相交于点E、F、G、H,且PC∥平面α,求证:
(1)AB⊥EH;
(2)FG∥面PAC.
18.(12分)在△ABC中,已知AB=2,AC=3,BC=.
(1)求角A的大小;
(2)求cos(B﹣C)的值.
19.(12分)如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC.
(1)证明:平面PAC⊥平面PBC;
(2)设PA=3,,求点A到平面PBC的距离.
20.(12分)已知,若,,求sin(α﹣β)的值.
21.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且cosA=,tan(B﹣A)=.
(1)求tanB的值;
(2)若c=13,求△ABC的面积.
22.(12分)某小区内有一块以O为圆心半径为20米的圆形区域.广场,为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形OAB区域,其中两个端点A,B分别在圆周上;观众席为梯形ABQP内且在圆O外的区域,其中AP=AB=BQ,∠PAB=∠QBA=120°,且AB,PQ在点O的同侧.为保证视听效果,要求观众席内每一个观众到舞台O处的距离都不超过60米.设.
(1)求AB的长(用α表示);
(2)对于任意α,上述设计方案是否均能符合要求?
2018-2019学年江苏省宿迁市沭阳县高一(下)期中数学试卷
参考答案与试题解析
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:sin17°cos13°+cos17°sin13°
=sin(17°+13°)
=sin30°
=.
故选:B.
2.【解答】解:△ABC中,角A,B,C的对边边长分别为a,b,c,
若a=2,b=3,C=120°,
则S△ABC=ab×sin120°=×2×3×=,
故选:C.
3.【解答】解:△ABC中,A:B:C=1:1:4,
所以三个内角分别为30°,30°,120°;
则a:b:c=sinA:sinB:sinC
=::
=1:1:.
故选:A.
4.【解答】解:对于A,两两相交且不共点的三条直线确定一个平面,
如三角形所在的三边确定一个平面,∴A正确;
对于B,经过一条直线和一个点不一定能确定一个平面,
如点在直线上时,∴B错误;
对于C,经过不在同一条直线上的三点确定一个平面,∴C错误;
对于D,空间四边形不能确定一个平面,∴D错误.
故选:A.
5.【解答】解:由题意得,y=2cos2(x+)﹣1=cos2(x+)=cos(2x+)=﹣sin2x,
∴函数的最小正周期是π,且是奇函数,
故选:C.
6.【解答】解:∵在△ABC中,a2=b2+c2﹣bc,即b2+c2﹣a2=bc,
∴cosA==,
则A=60°,
故选:D.
7.【解答】解:取CC1的中点G,连EG,BC1,
易得EF∥BC1∥AD1,
所以异面直线AD1与EF所成角是∠FEG或其补角,
在三角形EFG中,EF=EG=FG,∴∠FEG=60°.
故选:C.
8.【解答】解:扇形的弧长等于6×=2π,
所以圆锥的底面周长为2π,底面半径为1,
∴圆锥的高为=.
故选:A.
9.【解答】解:∵△ABC中,,
∴根据正弦定理得:sinA=sinB=2sinBcosB,
∵sinB>0,
∴cosB=.
故选:D.
10.【解答】解:△ABC中,∵bcosC+ccosB=asinA,
∴由正弦定理得:sinBcosC+sinCcosB=sin2A,
即sin(B+C)=sin(π﹣A)=sinA=sin2A,又sinA>0,
∴sinA=1,A∈(0,π),
∴A=.
∴△ABC的形状是直角三角形,
故选:C.
11.【解答】解:∵,D1C⊥平面BCC1B1,
∴H到平面BCC1B1的距离h=D1C=2,
又S△BCM==3,
∴VM﹣BCH=VH﹣BCM==2.
故选:B.
12.【解答】解:∵由正弦定理可得:==2,
∴b+c
=2sinB+2sinC
=2sinB+2sin(﹣B)
=2sinB+2(cosB+sinB)
=3sinB+cosB
=2sin(B+),
∵B,C为锐角,B+C=,
∴B∈(,),可得:B+∈(,),
∴sin(B+)∈(,1],
∴b+c=2sin(B+)∈(3,2],
故选:D.
二、填空题:本题共4小题,每小题5分,共20分.
13.【解答】解:∵sinα﹣2cosα=0,可得:sina=2cosa,即tanα=2,
∴tan2α===﹣.
故答案为:﹣.
14.【解答】解:∵,
∴由余弦定理可得:BC2=AB2+AC2﹣2AB?AC?cosA=16+4﹣2×=16,解得:BC=4,
∴BD=2,
∴在△ABC中,可得:cosB===,
∴在△ABD中,由余弦定理可得:AD2=AB2+BD2﹣2AB?BD?cosB=16+4﹣2×4×2×=6,
∴解得:AD=.
故答案为:.
15.【解答】解:设f(x)=cos2x﹣2cosx=2cos2x﹣2cosx﹣1=2(cosx﹣)2﹣,
又cosx∈[﹣1,1],
所以﹣≤f(x)≤3,
又关于x的方程cos2x﹣2cosx=m﹣1有实数解,
所以﹣≤m﹣1≤3,
即≤m≤4,
故答案为:[﹣].
16.【解答】解:把三棱锥O﹣ABC补形为长方体,则长方体的对角线长为.
∴三棱锥O﹣ABC的外接球的半径为R=.
由题意,,即x=3.
故答案为:3.
三、解答题:本大题共6小题,共计70分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
17.【解答】证明:(1)∵AB⊥AC,AB⊥AP.
又AC?平面PAC,AP?平面PAC,AC∩AP=A,
∴AB⊥平面PAC,…3分
又EH?面PAC,∴AB⊥EH.…4分
(2)∵PC∥平面α,平面PAC∩平面α=FG,
PC?平面PAC,∴PC∥FG,…7分
又PC?面PAC,FG?面PAC
∴FG∥面PAC.…10分
18.【解答】解:(1)∵AB=2,AC=3,BC=.
∴由余弦定理可得:cosA===,…2分
∵A∈(0,π),
∴A=…5分
(2)由正弦定理:,可得sinC===.
∵AB<BC,
∴C<A,即0,可得:cosC===,…8分
∴sin2C=2sinCcosC=2×=,cos2C=2cos2C﹣1=2×﹣1=,…11分
∵A+B+C=π,A=,可得:B=﹣C,
∴cos(B﹣C)=cos(﹣2C)=coscos2C+sinsin2C=(﹣)×+×=…14分
19.【解答】(1)证明:∵AB是⊙O的直径,点C是⊙O上的动点,
∴∠ACB=90°,即BC⊥AC.………………………2分
又∵PA垂直于⊙O所在的平面ABC,BC?平面⊙O,
∴PA⊥BC………………………………………………4分
又PA∩AC=A,
∴BC⊥平面PAC.
又BC?平面PBC,
∴平面PAC⊥平面PBC.………………………6分
(2)解:由(1)知平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,
过A点作PC的垂线,垂足为D,显然AD⊥平面PBC,
即AD为三棱锥A﹣PBC的高…10分
在Rt△PAC中,,所以,
由AD×PC=PA×AC,得
即点A到平面PCB的距离为,
三棱锥点A到平面PBC的距离:…12分
20.【解答】解:由,得,…2分
由,得;…4分
,得…6分
所以…9分
==…12分
21.【解答】解:(1)在△ABC中,由cosA=,得A为锐角,所以sinA=,
所以tanA==,
所以tanB=tan[(B﹣A)+A]===3;
(2)在三角形ABC中,由tanB=3,
所以sinB=,cosB=,
由sinC=sin(A+B)=sinAcosB+cosAsinB=,
由正弦定理=,得b===15,
所以△ABC的面积S=bcsinA=×15×13×=78.
22.【解答】解:(1)过点O作OH垂直于AB,垂足为H.
在直角三角形OHA中,OA=20,∠OAH=α,
所以AH=20cosα,因此AB=2AH=40cosα…3分
(2)由图可知,点P处的观众离点O最远…5分
在三角形OAP中,由余弦定理可知
=
=
=…9分
因为,所以当,即时,
(OP2)max=800+1600,
又(OP2)max=800+1600<3600
所以(OP)max<60…11分
所以观众席内每一个观众到舞台O处的距离都不超过60米.
故对于任意α,上述设计方案均能符合要求…12分
同课章节目录
