人教高中数学 选修2-3 第三章 3.1回归分析的基本思想及其初步应用 课件(25张ppt)
文档属性
| 名称 | 人教高中数学 选修2-3 第三章 3.1回归分析的基本思想及其初步应用 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 429.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-03 00:00:00 | ||
图片预览






文档简介
3.1回归分析的基本思想及其初步应用
高二数学 选修2-3
郑平正 制作
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
问题2:某水田水稻产量y与施肥量x之间是否
有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上
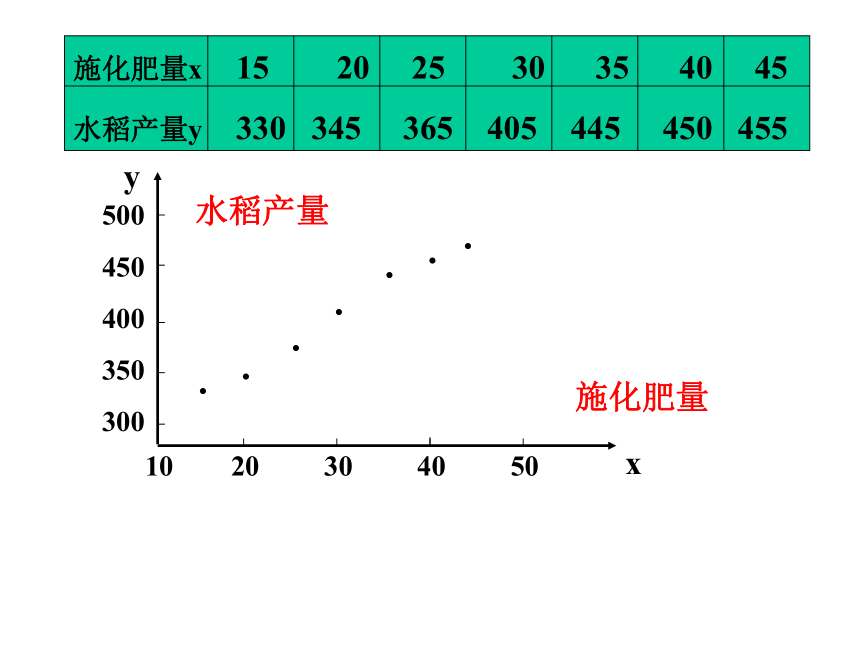
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
复习 变量之间的两种关系
郑平正 制作
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量
水稻产量
郑平正 制作
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1、定义:
1):相关关系是一种不确定性关系;
注
郑平正 制作
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
探索:水稻产量y与施肥量x之间大致有何规律?
郑平正 制作
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
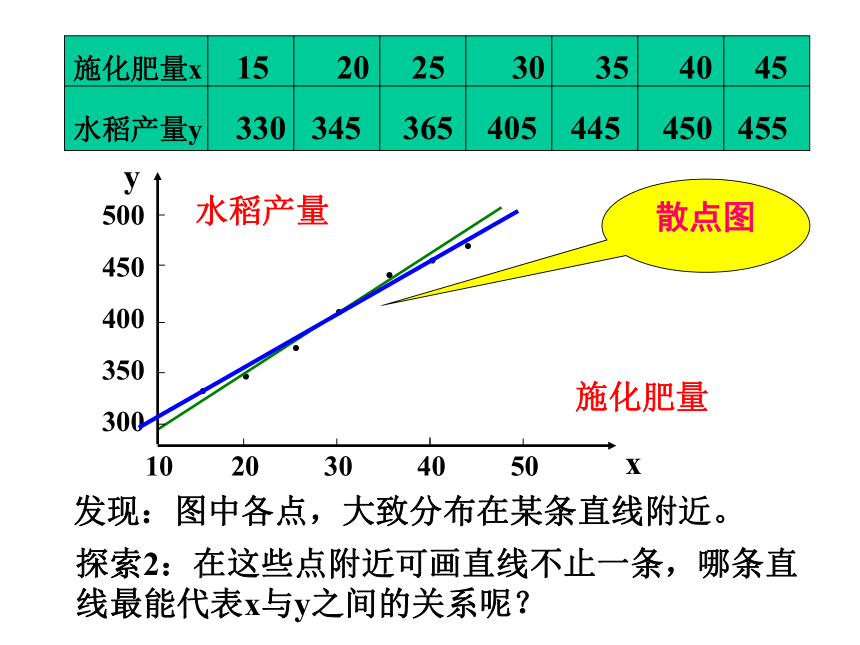
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
散点图
施化肥量
水稻产量
郑平正 制作
探究
对于一组具有线性相关关系的数据
我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:
郑平正 制作
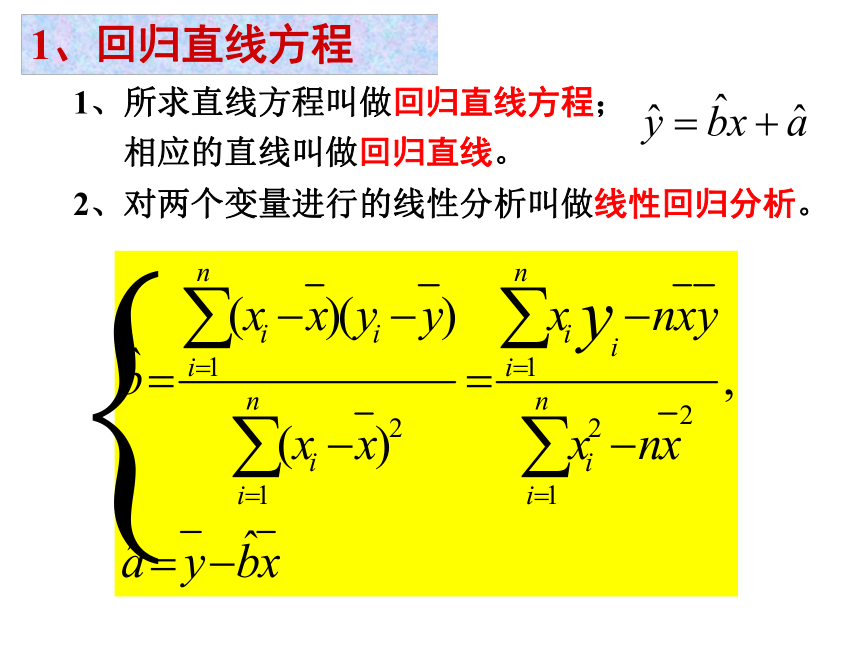
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
1、回归直线方程
郑平正 制作
2、求回归直线方程的步骤:
郑平正 制作
例1、观察两相关量得如下数据:
求两变量间的回归方程.
解:列表:
x -1 -2 -3 -4 -5 5 3 4 2 1
y -9 -7 -5 -3 -1 1 5 3 7 9
i 1 2 3 4 5 6 7 8 9 10
xi -1 -2 -3 -4 -5 5 3 4 2 1
yi -9 -7 -5 -3 -1 1 5 3 7 9
xiyi 9 14 15 12 5 5 15 12 14 9
郑平正 制作
所求回归直线方程为
郑平正 制作
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归直线上。这些点散布在回归直线附近。
郑平正 制作
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
(一)我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
3、残差分析:
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
郑平正 制作
残差图的制作及作用
1、坐标纵轴为残差变量,横轴可以有不同的选择;
2、若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3、对于远离横轴的点,要特别注意。
郑平正 制作
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
(一)我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
3、残差分析:
(二)
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
郑平正 制作
例2 在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
列出残差表为
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
郑平正 制作
例3 关于x与y有如下数据:
有如下的两个线性模型:
(1) ;(2)
试比较哪一个拟合效果更好。
x 2 4 5 6 8
y 30 40 60 50 70
郑平正 制作
7、一般地,建立回归模型的基本步骤为:
郑平正 制作
什么是回归分析?
(内容)
从一组样本数据出发,确定变量之间的数学关系式
对这些关系式的可信程度进行各种统计检验,并从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著
利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确程度
郑平正 制作
回归分析与相关分析的区别
相关分析中,变量 x 变量 y 处于平等的地位;回归分析中,变量 y 称为因变量,处在被解释的地位,x 称为自变量,用于预测因变量的变化
相关分析中所涉及的变量 x 和 y 都是随机变量;回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量
相关分析主要是描述两个变量之间线性关系的密切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控制
郑平正 制作
例3、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:
(1)y与x是否具有线性相关关系;
(2)如果具有线性相关关系,求回归直线方程;
(3)预测当钢水含碳量为160个0.01%时,应冶炼多少分钟?
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
郑平正 制作
如何描述两个变量之间线性相关关系的强弱?
在《数学3》中,我们学习了用相关系数r来衡量两个变量
之间线性相关关系的方法。
相关系数r
r>0正相关;r<0负相关。 通常,r>0.75或r<-0.75认为两个变量有很强的相关性.
郑平正 制作
相关关系的测度
(相关系数取值及其意义)
r
郑平正 制作
(1)列出下表,并计算
故,钢水含碳量与冶炼时间具有很强线性相关性
i 1 2 3 4 5 6 7 8 9 10
xi 104 180 190 177 147 134 150 191 204 121
yi 100 200 210 185 155 135 170 205 235 125
xiyi 10400 36000 39900 32745 22785 18090 25500 39155 47940 15125
郑平正 制作
(2)设所求的回归方程为
郑平正 制作
高二数学 选修2-3
郑平正 制作
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
问题2:某水田水稻产量y与施肥量x之间是否
有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
复习 变量之间的两种关系
郑平正 制作
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量
水稻产量
郑平正 制作
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1、定义:
1):相关关系是一种不确定性关系;
注
郑平正 制作
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
探索:水稻产量y与施肥量x之间大致有何规律?
郑平正 制作
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
散点图
施化肥量
水稻产量
郑平正 制作
探究
对于一组具有线性相关关系的数据
我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:
郑平正 制作
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
1、回归直线方程
郑平正 制作
2、求回归直线方程的步骤:
郑平正 制作
例1、观察两相关量得如下数据:
求两变量间的回归方程.
解:列表:
x -1 -2 -3 -4 -5 5 3 4 2 1
y -9 -7 -5 -3 -1 1 5 3 7 9
i 1 2 3 4 5 6 7 8 9 10
xi -1 -2 -3 -4 -5 5 3 4 2 1
yi -9 -7 -5 -3 -1 1 5 3 7 9
xiyi 9 14 15 12 5 5 15 12 14 9
郑平正 制作
所求回归直线方程为
郑平正 制作
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归直线上。这些点散布在回归直线附近。
郑平正 制作
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
(一)我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
3、残差分析:
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
郑平正 制作
残差图的制作及作用
1、坐标纵轴为残差变量,横轴可以有不同的选择;
2、若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3、对于远离横轴的点,要特别注意。
郑平正 制作
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
(一)我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
3、残差分析:
(二)
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
郑平正 制作
例2 在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
列出残差表为
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
郑平正 制作
例3 关于x与y有如下数据:
有如下的两个线性模型:
(1) ;(2)
试比较哪一个拟合效果更好。
x 2 4 5 6 8
y 30 40 60 50 70
郑平正 制作
7、一般地,建立回归模型的基本步骤为:
郑平正 制作
什么是回归分析?
(内容)
从一组样本数据出发,确定变量之间的数学关系式
对这些关系式的可信程度进行各种统计检验,并从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著
利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确程度
郑平正 制作
回归分析与相关分析的区别
相关分析中,变量 x 变量 y 处于平等的地位;回归分析中,变量 y 称为因变量,处在被解释的地位,x 称为自变量,用于预测因变量的变化
相关分析中所涉及的变量 x 和 y 都是随机变量;回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量
相关分析主要是描述两个变量之间线性关系的密切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控制
郑平正 制作
例3、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:
(1)y与x是否具有线性相关关系;
(2)如果具有线性相关关系,求回归直线方程;
(3)预测当钢水含碳量为160个0.01%时,应冶炼多少分钟?
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
郑平正 制作
如何描述两个变量之间线性相关关系的强弱?
在《数学3》中,我们学习了用相关系数r来衡量两个变量
之间线性相关关系的方法。
相关系数r
r>0正相关;r<0负相关。 通常,r>0.75或r<-0.75认为两个变量有很强的相关性.
郑平正 制作
相关关系的测度
(相关系数取值及其意义)
r
郑平正 制作
(1)列出下表,并计算
故,钢水含碳量与冶炼时间具有很强线性相关性
i 1 2 3 4 5 6 7 8 9 10
xi 104 180 190 177 147 134 150 191 204 121
yi 100 200 210 185 155 135 170 205 235 125
xiyi 10400 36000 39900 32745 22785 18090 25500 39155 47940 15125
郑平正 制作
(2)设所求的回归方程为
郑平正 制作
