2019年高三物理冲刺---电学典型问题归纳总结 Word版含解析
文档属性
| 名称 | 2019年高三物理冲刺---电学典型问题归纳总结 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 526.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-05-02 00:00:00 | ||
图片预览



文档简介
2019年高三物理冲刺---电学典型问题归纳总结
一、带电粒子在电场中的运动问题
例1.如图所示,离子发生器发射出一束质量为、电荷量为的离子,从静止经加速电压进行加速.
(1)求经电场加速后获得速度的大小;
(2)若经电压加速后,离子从两平行板左侧中间位置平行两板射入电压的偏转电场.已知平行板长为,两板间距离为,求:
①离子离开电场前在偏转电场中的运动时间;
②离子在偏转电场中受到的电场力的大小;
③离子在偏转电场中的加速度;
④离子在离开偏转电场时的纵向速度;
⑤离子在离开偏转电场时的速度的大小;
⑥离子在离开偏转电场时的竖直偏移量;
⑦离子离开偏转电场时的偏转角的正切值;
⑧证明离子飞出电场后的速度方向的反向延长线交于两板间的中心点;
⑨要使离子能穿出电场区域,则求两板间所加偏转电压的范围;
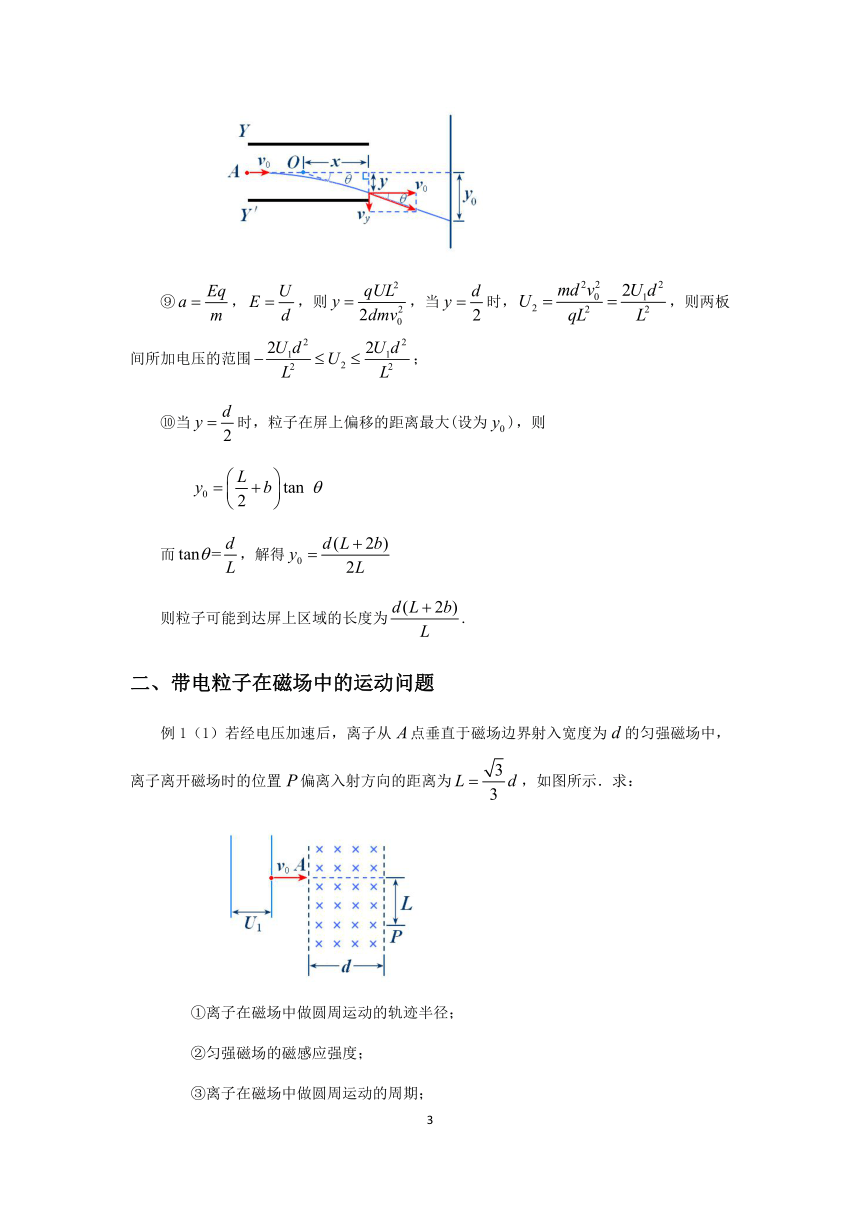
⑩若放置一足够大、与两板右侧相距的竖直屏,求粒子可能到达屏上区域的长度.
【解析】(1)不管加速电场是不是匀强电场,都适用,所以由动能定理得
解得
.
(2)①由于偏转电场是匀强电场,所以离子的运动是类平抛运动,即水平方向为速度为v0的匀速直线运动,竖直方向为初速度为零的匀加速直线运动,所以
;
②,;
③;
④;
⑤;
⑥ (与带电粒子的无关,只取决于加速电场和偏转电场);
⑦;
⑧如图所示,,,,,所以;
⑨,,则,当时,,则两板间所加电压的范围;
⑩当时,粒子在屏上偏移的距离最大(设为),则
而,解得
则粒子可能到达屏上区域的长度为.
二、带电粒子在磁场中的运动问题
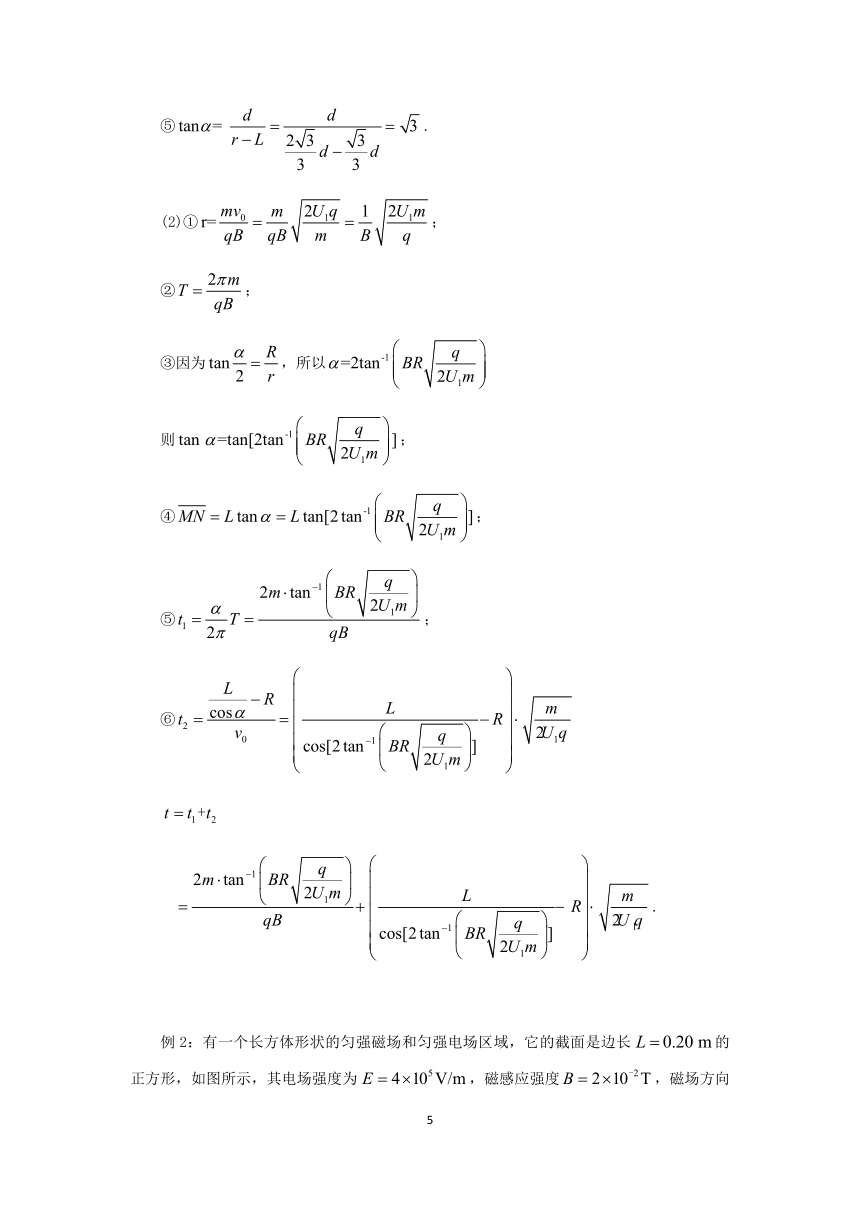
例1(1)若经电压加速后,离子从点垂直于磁场边界射入宽度为的匀强磁场中,离子离开磁场时的位置偏离入射方向的距离为,如图所示.求:
①离子在磁场中做圆周运动的轨迹半径;
②匀强磁场的磁感应强度;
③离子在磁场中做圆周运动的周期;
④离子在磁场中的运动时间;
⑤离子离开磁场时速度偏转的角度的正切值.
(2)若经电压加速后,离子沿方向进入一半径为、磁感应强度为的圆形匀强磁场区域,离开磁场后离子将击中屏幕的点,如图所示.已知点为屏幕的中心,磁场区域的圆心在的连线上,点与点的距离为.求:
①离子在磁场中做圆周运动的轨迹半径;
②离子在磁场中做圆周运动的周期;
③离子离开磁场时速度偏转的角度的正切值;
④离子击中的点与屏幕中心点的距离;
⑤离子在磁场中的运动时间;
⑥离子从进入圆形磁场到击中屏幕的总时间.
【解析】(1)①因为,所以解得;
②;
③;
④;
⑤.
(2)①;
②;
③因为,所以
则;
④;
⑤;
⑥
.
例2:有一个长方体形状的匀强磁场和匀强电场区域,它的截面是边长的正方形,如图所示,其电场强度为,磁感应强度,磁场方向垂直纸面向里,当一束质荷比为的正离子流,以一定的速度从电磁场的正方形区域边界的中点射入时,不计正离子的重力,则:
(1)要使离子流穿过电磁场区域而不发生偏转,电场强度的方向如何?离子流的速度多大?
(2)在离电磁场区域右边界处有一与边界平行的荧光屏,若撤去电场,离子流击中屏上 点;若撤去磁场,离子流击中屏上点,求间的距离.
【答案】见解析。
【解析】(1)电场方向竖直向下,与磁场构成粒子速度选择器,
使离子运动不偏转,则
,
解得
.
(2)撤去电场,离子在磁场中做匀速圆周运动,所需向心力
为洛伦兹力,于是
,
解得
离子离开磁场区域边界时,如图甲所示,对偏转角有
得
偏转距离
离开磁场后离子做匀速直线运动,故总的偏转距离为
解得
若撤去磁场,离子在电场中做匀变速曲线运动
通过电场的时间
加速度
偏转距离
偏转角为,如图乙所示,则,而
离开电场后离子做匀速直线运动,故总的偏离距离
解得
所以间的距离
.
三、电磁感应综合问题
例1.如图所示,在一磁感应强度的匀强磁场中,垂直于磁场方向水平放置着两根相距为的平行金属导轨和,导轨电阻忽略不计,在两根导轨的端点之间连接着一阻值的电阻.导轨上跨放着一根长为、每米长电阻为的金属棒,金属棒
与导轨正交放置,交点为,当金属棒在水平拉力的作用下以速度向左做匀速运动时,试求:
①电阻中的电流强度大小和方向;
②使金属棒做匀速运动的拉力;
③金属棒 两端点间的电势差;
④回路中的发热功率.
【答案】
【解析】金属棒向左匀速运动时,等效电路如图所示.在闭合回路中,金属棒部分相当于电源,内阻,电动势.
①根据欧姆定律,中的电流强度为
方向从经到.
②使金属棒匀速运动的外力与安培力是一对平衡力,方向向左,大小为
F.
③金属棒两端的电势差等于与三者之和,由于,所以
.
④回路中的热功率
.
【变式1】如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为。一个质量为、边长也为、匝数为的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行。时刻导线框的上边恰好与磁场的下边界重合(图中位置),导线框的速度为。经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置),导线框的速度刚好为零。
此后,导线框下落,经过一段时间回到初始位置。以向下为正,请定性画出上升、下降的过程的安培力随时间的变化图线。
【答案】
【变式2】如图所示,是两根足够长的固定平行金属导轨,两导轨间的距离为,导轨平面与水平面间的夹角为,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度为,在导轨的端连接一个阻值为的电阻,一根质量为、垂直于导轨放置的金属棒,从静止开始沿导轨下滑.已知金属棒与导轨间的动摩擦因数为,导轨和金属棒的电阻都不计.
①请分析金属棒的运动情况,并求此过程中金属棒的最大速度.
②若金属棒从静止开始沿导轨下滑到速度最大时,通过的位移为,能否求出在此过程中通过电阻的电荷量为多少?如果能,请求出该电荷量;如果不能,请说明原因.
③若金属棒从静止开始沿导轨下滑到速度最大时,通过的位移为,能否求出在此过程中安培力对金属棒所做的功?如果能,请求出安培力所做的功;如果不能,请说明原因.
【答案】
【解析】①运动情况分析:金属棒沿导轨加速下滑→感应电动势增大→感应电流增大→导体在磁场中所受安培力变大→合外力减小→加速度减小→直到当时,最大.
金属棒下滑时因切割磁感线,产生感应电动势,根据法拉第电磁感应定律可得
闭合电路中将产生感应电流,根据闭合电路欧姆定律可得
;
根据右手定则可判定感应电流方向为;再根据左手定则判断金属棒所受的安培力方向如图所示,其大小为
,
由以上三式可得
对金属棒所受的力进行正交分解,有
,
.
以金属棒为研究对象,根据牛顿第二定律有
金属棒做加速度减小的加速运动,当时速度达到最大值,即
可解得
.
②能求出通过电阻的电荷量.金属棒 下滑过程中虽然做变加速运动,但计算电荷量应该用感应电流的平均值来计算.由法拉第电磁感应定律得,平均感应电动势,平均电流,通过电阻R的电荷量
.
③能求出安培力所做的功.金属棒下滑过程中重力做正功,重力势能减少
,
动能增加
,
摩擦产生的热量
,
由能量守恒定律可知,电阻R产生的电热
.
根据功能关系,在金属棒下滑过程中克服安培力所做的功等于电路中产生的电能,即安培力所做的功
.
例2:如图甲所示,质量的金属棒从某一高度由静止沿光滑的弧形轨道下滑,然后进入宽的光滑水平导轨, 水平导轨处于竖直向下、磁感应强度的广阔匀强磁场中.在水平导轨上另有一静止的金属棒,其质量与金属棒的质量相等.已知金属棒和的电阻分别是,金属棒进入水平导轨后,金属棒和运动的图象如图乙所示,导轨的电阻不计,整个水平导轨足够长.(取)求:
①金属棒的初始位置距水平轨道的高度.
②金属棒进入磁场的瞬间,金属棒的加速度多大?
③证明两棒的最终速度.
④若假设两棒始终没有相碰,则两棒在运动过程中最多产生多少电能?
⑤棒产生的总热量为多少?
⑥若轨道变成图丙所示,已知,两棒由同种材料制成且粗细相同,现给一个初速度,求稳定后 的速度.
⑦图甲中虚线处为磁场的边界,为使两棒不相撞,则棒离磁场边界(虚线处)至少多远?
【答案】见解析。
【解析】①金属棒进入水平轨道前机械能守恒,有
由图象知棒进入磁场的速度
解得
.
②由法拉第电磁感应定律得
.
故
所以
解得
.
③证明:棒进入磁场后,减速、加速,回路产生的感应电动势减小,直到时,两棒一起以匀速运动.对两棒,由动量守恒
,
得
.
④回路产生的电能等于棒克服安培力所做的功,等于棒损失的动能,即
.
⑤由能量守恒定律得
.
⑥稳定后,回路电流为,则
得
在运动过程中,对有
对有
由于
得
(注意:此问题中组成的系统动量不守恒)
联立解得,.
⑦在进入磁场到稳定的过程中,两棒距离逐渐减小,当两棒速度相等时,相距最近,设相对靠近了
对有
又因为
得
所以,棒距磁场边界至少为.
(
1
)
一、带电粒子在电场中的运动问题
例1.如图所示,离子发生器发射出一束质量为、电荷量为的离子,从静止经加速电压进行加速.
(1)求经电场加速后获得速度的大小;
(2)若经电压加速后,离子从两平行板左侧中间位置平行两板射入电压的偏转电场.已知平行板长为,两板间距离为,求:
①离子离开电场前在偏转电场中的运动时间;
②离子在偏转电场中受到的电场力的大小;
③离子在偏转电场中的加速度;
④离子在离开偏转电场时的纵向速度;
⑤离子在离开偏转电场时的速度的大小;
⑥离子在离开偏转电场时的竖直偏移量;
⑦离子离开偏转电场时的偏转角的正切值;
⑧证明离子飞出电场后的速度方向的反向延长线交于两板间的中心点;
⑨要使离子能穿出电场区域,则求两板间所加偏转电压的范围;
⑩若放置一足够大、与两板右侧相距的竖直屏,求粒子可能到达屏上区域的长度.
【解析】(1)不管加速电场是不是匀强电场,都适用,所以由动能定理得
解得
.
(2)①由于偏转电场是匀强电场,所以离子的运动是类平抛运动,即水平方向为速度为v0的匀速直线运动,竖直方向为初速度为零的匀加速直线运动,所以
;
②,;
③;
④;
⑤;
⑥ (与带电粒子的无关,只取决于加速电场和偏转电场);
⑦;
⑧如图所示,,,,,所以;
⑨,,则,当时,,则两板间所加电压的范围;
⑩当时,粒子在屏上偏移的距离最大(设为),则
而,解得
则粒子可能到达屏上区域的长度为.
二、带电粒子在磁场中的运动问题
例1(1)若经电压加速后,离子从点垂直于磁场边界射入宽度为的匀强磁场中,离子离开磁场时的位置偏离入射方向的距离为,如图所示.求:
①离子在磁场中做圆周运动的轨迹半径;
②匀强磁场的磁感应强度;
③离子在磁场中做圆周运动的周期;
④离子在磁场中的运动时间;
⑤离子离开磁场时速度偏转的角度的正切值.
(2)若经电压加速后,离子沿方向进入一半径为、磁感应强度为的圆形匀强磁场区域,离开磁场后离子将击中屏幕的点,如图所示.已知点为屏幕的中心,磁场区域的圆心在的连线上,点与点的距离为.求:
①离子在磁场中做圆周运动的轨迹半径;
②离子在磁场中做圆周运动的周期;
③离子离开磁场时速度偏转的角度的正切值;
④离子击中的点与屏幕中心点的距离;
⑤离子在磁场中的运动时间;
⑥离子从进入圆形磁场到击中屏幕的总时间.
【解析】(1)①因为,所以解得;
②;
③;
④;
⑤.
(2)①;
②;
③因为,所以
则;
④;
⑤;
⑥
.
例2:有一个长方体形状的匀强磁场和匀强电场区域,它的截面是边长的正方形,如图所示,其电场强度为,磁感应强度,磁场方向垂直纸面向里,当一束质荷比为的正离子流,以一定的速度从电磁场的正方形区域边界的中点射入时,不计正离子的重力,则:
(1)要使离子流穿过电磁场区域而不发生偏转,电场强度的方向如何?离子流的速度多大?
(2)在离电磁场区域右边界处有一与边界平行的荧光屏,若撤去电场,离子流击中屏上 点;若撤去磁场,离子流击中屏上点,求间的距离.
【答案】见解析。
【解析】(1)电场方向竖直向下,与磁场构成粒子速度选择器,
使离子运动不偏转,则
,
解得
.
(2)撤去电场,离子在磁场中做匀速圆周运动,所需向心力
为洛伦兹力,于是
,
解得
离子离开磁场区域边界时,如图甲所示,对偏转角有
得
偏转距离
离开磁场后离子做匀速直线运动,故总的偏转距离为
解得
若撤去磁场,离子在电场中做匀变速曲线运动
通过电场的时间
加速度
偏转距离
偏转角为,如图乙所示,则,而
离开电场后离子做匀速直线运动,故总的偏离距离
解得
所以间的距离
.
三、电磁感应综合问题
例1.如图所示,在一磁感应强度的匀强磁场中,垂直于磁场方向水平放置着两根相距为的平行金属导轨和,导轨电阻忽略不计,在两根导轨的端点之间连接着一阻值的电阻.导轨上跨放着一根长为、每米长电阻为的金属棒,金属棒
与导轨正交放置,交点为,当金属棒在水平拉力的作用下以速度向左做匀速运动时,试求:
①电阻中的电流强度大小和方向;
②使金属棒做匀速运动的拉力;
③金属棒 两端点间的电势差;
④回路中的发热功率.
【答案】
【解析】金属棒向左匀速运动时,等效电路如图所示.在闭合回路中,金属棒部分相当于电源,内阻,电动势.
①根据欧姆定律,中的电流强度为
方向从经到.
②使金属棒匀速运动的外力与安培力是一对平衡力,方向向左,大小为
F.
③金属棒两端的电势差等于与三者之和,由于,所以
.
④回路中的热功率
.
【变式1】如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为。一个质量为、边长也为、匝数为的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行。时刻导线框的上边恰好与磁场的下边界重合(图中位置),导线框的速度为。经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置),导线框的速度刚好为零。
此后,导线框下落,经过一段时间回到初始位置。以向下为正,请定性画出上升、下降的过程的安培力随时间的变化图线。
【答案】
【变式2】如图所示,是两根足够长的固定平行金属导轨,两导轨间的距离为,导轨平面与水平面间的夹角为,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度为,在导轨的端连接一个阻值为的电阻,一根质量为、垂直于导轨放置的金属棒,从静止开始沿导轨下滑.已知金属棒与导轨间的动摩擦因数为,导轨和金属棒的电阻都不计.
①请分析金属棒的运动情况,并求此过程中金属棒的最大速度.
②若金属棒从静止开始沿导轨下滑到速度最大时,通过的位移为,能否求出在此过程中通过电阻的电荷量为多少?如果能,请求出该电荷量;如果不能,请说明原因.
③若金属棒从静止开始沿导轨下滑到速度最大时,通过的位移为,能否求出在此过程中安培力对金属棒所做的功?如果能,请求出安培力所做的功;如果不能,请说明原因.
【答案】
【解析】①运动情况分析:金属棒沿导轨加速下滑→感应电动势增大→感应电流增大→导体在磁场中所受安培力变大→合外力减小→加速度减小→直到当时,最大.
金属棒下滑时因切割磁感线,产生感应电动势,根据法拉第电磁感应定律可得
闭合电路中将产生感应电流,根据闭合电路欧姆定律可得
;
根据右手定则可判定感应电流方向为;再根据左手定则判断金属棒所受的安培力方向如图所示,其大小为
,
由以上三式可得
对金属棒所受的力进行正交分解,有
,
.
以金属棒为研究对象,根据牛顿第二定律有
金属棒做加速度减小的加速运动,当时速度达到最大值,即
可解得
.
②能求出通过电阻的电荷量.金属棒 下滑过程中虽然做变加速运动,但计算电荷量应该用感应电流的平均值来计算.由法拉第电磁感应定律得,平均感应电动势,平均电流,通过电阻R的电荷量
.
③能求出安培力所做的功.金属棒下滑过程中重力做正功,重力势能减少
,
动能增加
,
摩擦产生的热量
,
由能量守恒定律可知,电阻R产生的电热
.
根据功能关系,在金属棒下滑过程中克服安培力所做的功等于电路中产生的电能,即安培力所做的功
.
例2:如图甲所示,质量的金属棒从某一高度由静止沿光滑的弧形轨道下滑,然后进入宽的光滑水平导轨, 水平导轨处于竖直向下、磁感应强度的广阔匀强磁场中.在水平导轨上另有一静止的金属棒,其质量与金属棒的质量相等.已知金属棒和的电阻分别是,金属棒进入水平导轨后,金属棒和运动的图象如图乙所示,导轨的电阻不计,整个水平导轨足够长.(取)求:
①金属棒的初始位置距水平轨道的高度.
②金属棒进入磁场的瞬间,金属棒的加速度多大?
③证明两棒的最终速度.
④若假设两棒始终没有相碰,则两棒在运动过程中最多产生多少电能?
⑤棒产生的总热量为多少?
⑥若轨道变成图丙所示,已知,两棒由同种材料制成且粗细相同,现给一个初速度,求稳定后 的速度.
⑦图甲中虚线处为磁场的边界,为使两棒不相撞,则棒离磁场边界(虚线处)至少多远?
【答案】见解析。
【解析】①金属棒进入水平轨道前机械能守恒,有
由图象知棒进入磁场的速度
解得
.
②由法拉第电磁感应定律得
.
故
所以
解得
.
③证明:棒进入磁场后,减速、加速,回路产生的感应电动势减小,直到时,两棒一起以匀速运动.对两棒,由动量守恒
,
得
.
④回路产生的电能等于棒克服安培力所做的功,等于棒损失的动能,即
.
⑤由能量守恒定律得
.
⑥稳定后,回路电流为,则
得
在运动过程中,对有
对有
由于
得
(注意:此问题中组成的系统动量不守恒)
联立解得,.
⑦在进入磁场到稳定的过程中,两棒距离逐渐减小,当两棒速度相等时,相距最近,设相对靠近了
对有
又因为
得
所以,棒距磁场边界至少为.
(
1
)
同课章节目录
