人教版数学八年级下册课件 19.2.3一次函数与一元一次不等式课件(21张)
文档属性
| 名称 | 人教版数学八年级下册课件 19.2.3一次函数与一元一次不等式课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 809.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-02 17:57:01 | ||
图片预览






文档简介
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
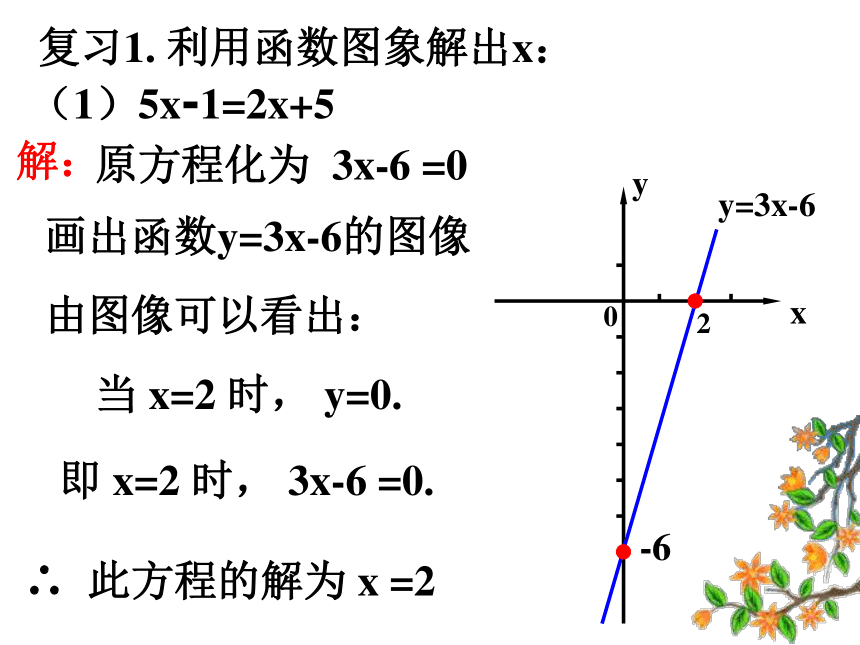
原方程化为 3x-6 =0
画出函数y=3x-6的图像
∴ 此方程的解为 x =2
y=3x-6
解:
由图像可以看出:
当 x=2 时, y=0.
复习1. 利用函数图象解出x:
(1)5x-1=2x+5
即 x=2 时, 3x-6 =0.
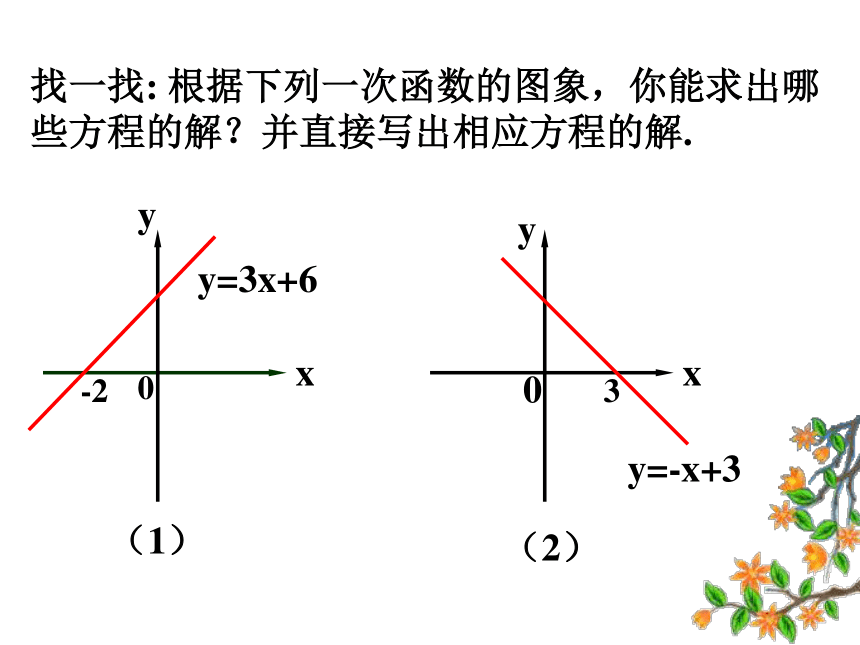
找一找: 根据下列一次函数的图象,你能求出哪些方程的解?并直接写出相应方程的解.
“解方程ax+b=0(a,b为常数,a≠0)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?
(同一个问题)
“解方程ax+b=0(a,b为常数,a≠0)”
与“一次函数y=ax+b的图像与X
轴的交点的横坐标有什么关系?
我们来看下面的问题
1. 解不等式:5x+6>3x+10
这两个问题有什么关系?
2. 当自变量x为何值时,函数y=2x-4值大于0?
问题1中,不等式可化为 2x-4>0,
解得 x>2
问题2中,是要解不等式 2x-4>0,
得出 x>2 时,
函数y=2x-4值大于0.
《一次函数与一元一次不等式》
1. 是不是所有的一元一次不等式都可以转化为一次函数的相关问题呢?
2. 它在函数图像上的表现是什么呢?
3. 如何通过函数图像来求解一元一次不等式?
以上这些问题就是我们这一节将要学习的问题.
y=2x-4
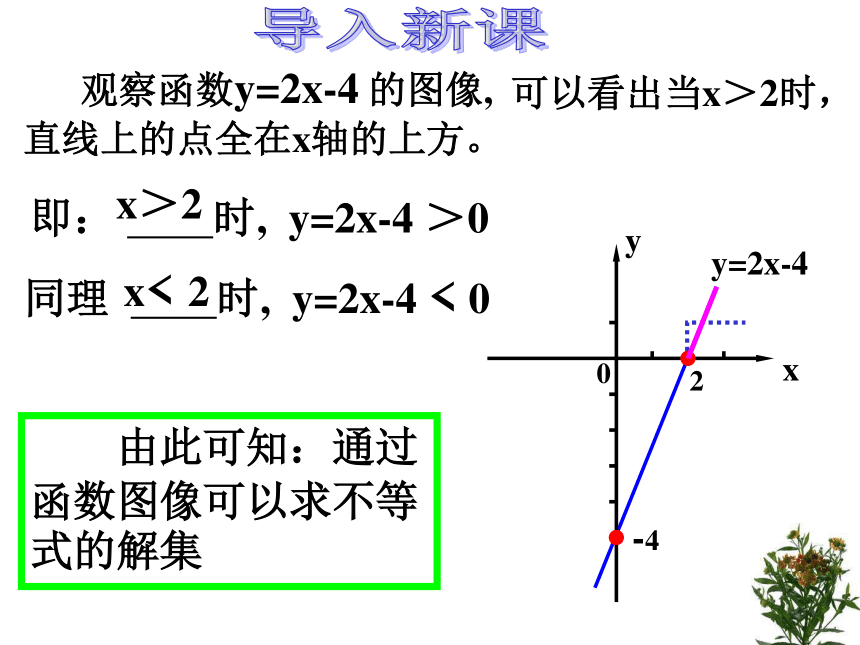
可以看出当x>2时,直线上的点全在x轴的上方。
即: 时, y=2x-4 >0
由此可知:通过函数图像可以求不等式的解集
同理 时, y=2x-4 < 0
观察函数y=2x-4 的图像,
x>2
x< 2
“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?
(同一个问题)
由于任何一元一次不等式都可以转化为ax+b>0或ax +b <0(a,b为常数,a≠0)的形式,
由于任何一元一次不等式都可以转化为ax+b >0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大于或小于0时,求自变量相应的取值范围。
例 用画函数图象的方法解不等式:
不等式化为 3x-6 <0
画出函数y=3x-6的图像
这时 y=3x-6 <0
∴ 此不等式的解集为x <2
y=3x-6
5x+4<2x+10
解:
由图像可以看出:
当 x<2 时这条直线上的点在x轴的下方,
解法二:
把 5x+4<2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图像.
10
-5
y=2x+10
y=5x+4
2
它们的交点的横坐标为2.
当x <2时直线y=5x+4 上的点都在直线y=2x+10的下方.
x <2
14
4
由图像可知
即5x+4<2x+10
∴此不等式的解集为
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
从数的角度看:
从形的角度看:
找一找: 根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应不等式的解集.
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y= -7
(2)y<2
-5
-7
8
解:
(1)画直线 y=3x+8
由图象可知
y=-7 时对应的 x=-5
∴ 当x=-5时, y=-7
y=3x+8
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y= -7
(2)y<2
-5
15
解法二:
画直线 y=3x+15,
由图象可知
当x=-5时, 3x+15 =0
y=3x+15
要使y= -7,
即3x+8 = -7,变为3x+15 =0
∴ 当x=-5时, y=-7
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
-2
2
8
解:
(2)画直线 y=3x+8
由图象可知
y<2 时对应的 x<-2
∴ 当x<-2时, y<2
y=3x+8
通过这节课的学习,你有什么收获?
用一次函数图象来解一元一次不等式
一次函数、一元一次不等式之间的联系
谢谢,再见
——毕达哥拉斯
原方程化为 3x-6 =0
画出函数y=3x-6的图像
∴ 此方程的解为 x =2
y=3x-6
解:
由图像可以看出:
当 x=2 时, y=0.
复习1. 利用函数图象解出x:
(1)5x-1=2x+5
即 x=2 时, 3x-6 =0.
找一找: 根据下列一次函数的图象,你能求出哪些方程的解?并直接写出相应方程的解.
“解方程ax+b=0(a,b为常数,a≠0)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?
(同一个问题)
“解方程ax+b=0(a,b为常数,a≠0)”
与“一次函数y=ax+b的图像与X
轴的交点的横坐标有什么关系?
我们来看下面的问题
1. 解不等式:5x+6>3x+10
这两个问题有什么关系?
2. 当自变量x为何值时,函数y=2x-4值大于0?
问题1中,不等式可化为 2x-4>0,
解得 x>2
问题2中,是要解不等式 2x-4>0,
得出 x>2 时,
函数y=2x-4值大于0.
《一次函数与一元一次不等式》
1. 是不是所有的一元一次不等式都可以转化为一次函数的相关问题呢?
2. 它在函数图像上的表现是什么呢?
3. 如何通过函数图像来求解一元一次不等式?
以上这些问题就是我们这一节将要学习的问题.
y=2x-4
可以看出当x>2时,直线上的点全在x轴的上方。
即: 时, y=2x-4 >0
由此可知:通过函数图像可以求不等式的解集
同理 时, y=2x-4 < 0
观察函数y=2x-4 的图像,
x>2
x< 2
“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?
(同一个问题)
由于任何一元一次不等式都可以转化为ax+b>0或ax +b <0(a,b为常数,a≠0)的形式,
由于任何一元一次不等式都可以转化为ax+b >0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大于或小于0时,求自变量相应的取值范围。
例 用画函数图象的方法解不等式:
不等式化为 3x-6 <0
画出函数y=3x-6的图像
这时 y=3x-6 <0
∴ 此不等式的解集为x <2
y=3x-6
5x+4<2x+10
解:
由图像可以看出:
当 x<2 时这条直线上的点在x轴的下方,
解法二:
把 5x+4<2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图像.
10
-5
y=2x+10
y=5x+4
2
它们的交点的横坐标为2.
当x <2时直线y=5x+4 上的点都在直线y=2x+10的下方.
x <2
14
4
由图像可知
即5x+4<2x+10
∴此不等式的解集为
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
从数的角度看:
从形的角度看:
找一找: 根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应不等式的解集.
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y= -7
(2)y<2
-5
-7
8
解:
(1)画直线 y=3x+8
由图象可知
y=-7 时对应的 x=-5
∴ 当x=-5时, y=-7
y=3x+8
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y= -7
(2)y<2
-5
15
解法二:
画直线 y=3x+15,
由图象可知
当x=-5时, 3x+15 =0
y=3x+15
要使y= -7,
即3x+8 = -7,变为3x+15 =0
∴ 当x=-5时, y=-7
1. 当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
-2
2
8
解:
(2)画直线 y=3x+8
由图象可知
y<2 时对应的 x<-2
∴ 当x<-2时, y<2
y=3x+8
通过这节课的学习,你有什么收获?
用一次函数图象来解一元一次不等式
一次函数、一元一次不等式之间的联系
谢谢,再见
