2019年高考三轮冲刺 不等式(教案)
文档属性
| 名称 | 2019年高考三轮冲刺 不等式(教案) | 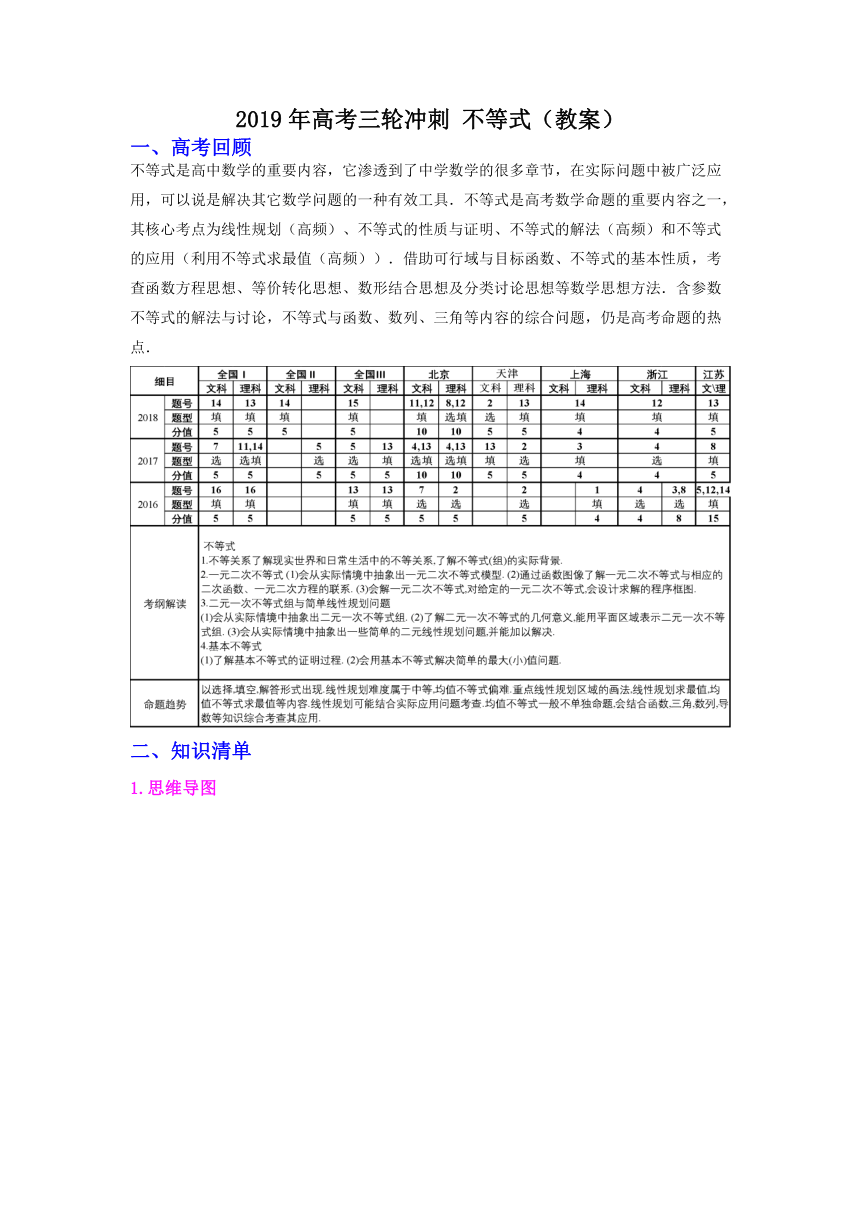 | |
| 格式 | zip | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-02 23:57:03 | ||
图片预览




文档简介
2019年高考三轮冲刺 不等式(教案)
一、高考回顾
不等式是高中数学的重要内容,它渗透到了中学数学的很多章节,在实际问题中被广泛应用,可以说是解决其它数学问题的一种有效工具.不等式是高考数学命题的重要内容之一,其核心考点为线性规划(高频)、不等式的性质与证明、不等式的解法(高频)和不等式的应用(利用不等式求最值(高频)).借助可行域与目标函数、不等式的基本性质,考查函数方程思想、等价转化思想、数形结合思想及分类讨论思想等数学思想方法.含参数不等式的解法与讨论,不等式与函数、数列、三角等内容的综合问题,仍是高考命题的热点.
知识清单
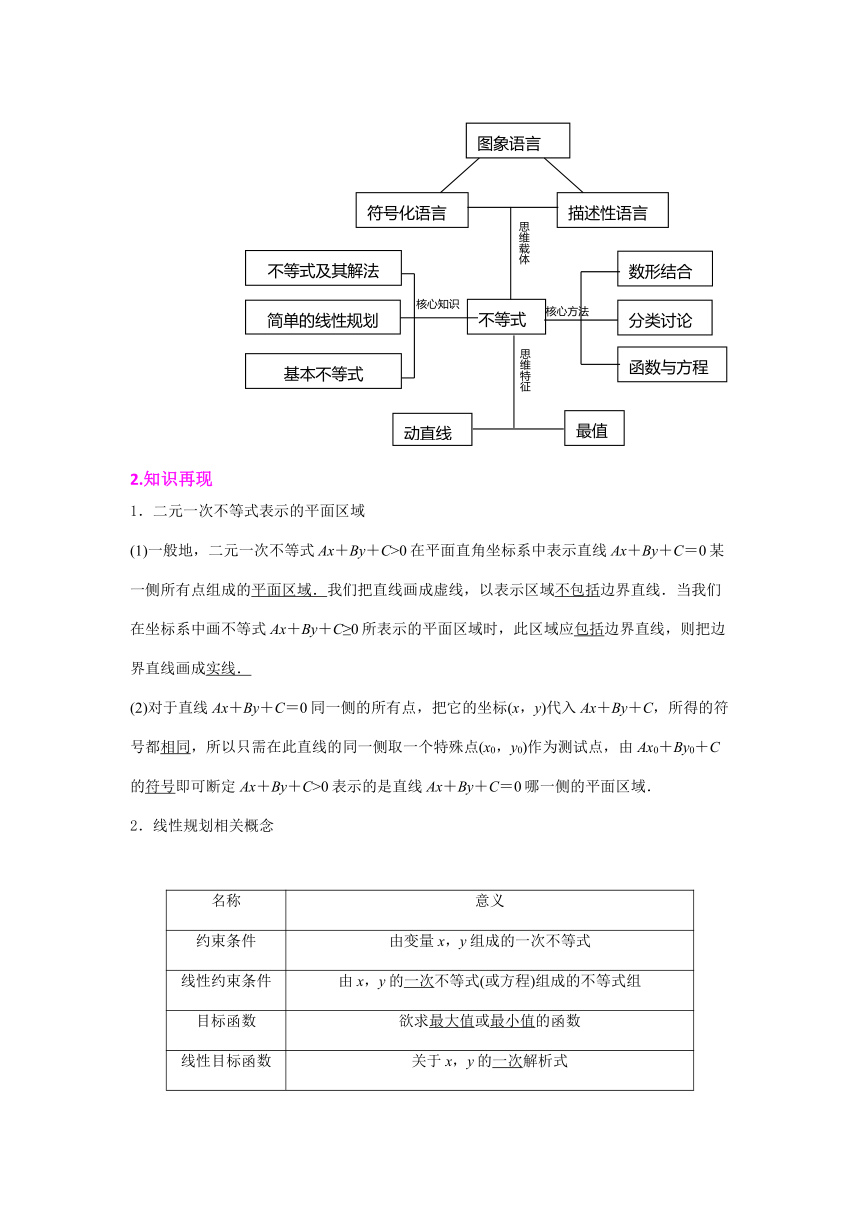
1.思维导图
(
核心方法
思维特征
动直线(
x,y
)
最值
不等式及其解法
简单的线性规划
基本不等式
核心知识
不等式
数形结合
分类讨论
函数与方程
图象语言
符号化语言
描述性语言
思维载体
)
2.知识再现
1.二元一次不等式表示的平面区域
(1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.我们把直线画成虚线,以表示区域不包括边界直线.当我们在坐标系中画不等式Ax+By+C≥0所表示的平面区域时,此区域应包括边界直线,则把边界直线画成实线.
(2)对于直线Ax+By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+By+C,所得的符号都相同,所以只需在此直线的同一侧取一个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号即可断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
2.线性规划相关概念
名称 意义
约束条件 由变量x,y组成的一次不等式
线性约束条件 由x,y的一次不等式(或方程)组成的不等式组
目标函数 欲求最大值或最小值的函数
线性目标函数 关于x,y的一次解析式
可行解 满足线性约束条件的解
可行域 所有可行解组成的集合
最优解 使目标函数取得最大值或最小值的可行解
线性规划问题 在线性约束条件下求线性目标函数的最大值或最小值问题
3.基本不等式:≤
(1)基本不等式成立的条件:a>0,b>0.
(2)等号成立的条件:当且仅当a=b时取等号.
4. 几个重要的不等式
(1)a2+b2≥2ab(a,b∈R).
(2)+≥2(a,b同号).
(3)ab≤(a,b∈R).
(4)≥ (a,b∈R).
以上不等式等号成立的条件均为a=b.
5. 算术平均数与几何平均数
设a>0,b>0,则a,b的算术平均数为,几何平均数为,基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数.
6.利用基本不等式求最值问题
已知x>0,y>0,则
(1)如果积是定值p,那么当且仅当x=y时,x+y有最小值2.(简记:积定和最小)
(2)如果和x+y是定值p,那么当且仅当x=y时,有最大值.(简记:和定积最大)
三、例题精讲
题型一 截距型线性规划问题
例1.(2018全国1).若,满足约束条件,则的最大值为_______________.
【答案】 6.
【解析】画出可行域如图所示,可知目标函数过点时取得最大值,.
例2.(2018·西安质检)若变量x,y满足则2x+y的取值范围为________.
【答案】[-2,2]
【解析】作出满足不等式组的平面区域如图中阴影部分所示,
平移直线2x+y=0,经过点A(1,0)时,2x+y取得最大值2×1+0=2,
经过点B(-1,0)时,2x+y取得最小值2×(-1)+0=-2,
所以2x+y的取值范围为[-2,2].
例3. (2018·黄冈联考)一个小型加工厂用一台机器生产甲、乙两种桶装饮料,生产一桶甲饮料需要白糖4千克,果汁18千克,用时3小时;生产一桶乙饮料需要白糖1千克,果汁15千克,用时1小时.现库存白糖10千克,果汁66千克,生产一桶甲饮料利润为200元,生产一桶乙饮料利润为100元,在使用该机器用时不超过9小时的条件下,生产甲、乙两种饮料利润之和的最大值为________.
【答案】 600
【解析】 设生产甲、乙两种饮料分别为x桶、y桶,利润为z元,
则得即
目标函数z=200x+100y.作出可行域(如图阴影部分所示),当直线z=200x+100y经过可行域上点B时,z取得最大值,解方程组得点B的坐标(2,2),故=200×2+100×2=600.
题型二 斜率型线性规划问题
例1.(2018·成都一诊)若实数x,y满足约束条件则的最小值为________.
【答案】-
【解析】作出不等式组表示的平面区域如图中阴影部分所示,
因为表示平面区域内的点与定点P(0,1)连线的斜率.
由图知,点P与点A连线的斜率最小,
所以min===-.
例2.已知实数,满足约束条件,则的取值范围为( )
A. B.
C. D.
【答案】 C
【解析】画出不等式表示的可行域,如图阴影三角形所示,
由题意得,.
由得,
所以可看作点和连线的斜率,记为,
由图形可得,
又,,所以,
因此或,所以的取值范围为.故选C.
例3.(2018·安徽江南十校联考)已知实数x,y满足,则z=的取值范围为________.
【答案】[0,1].
【解析】 作出不等式组对应的平面区域,如图阴影部分.z=表示区域内的点(x,y)与A(0,-1)连线的斜率k,由图可知,=0,,P为切点,设,=,
∴=,∴x0=1,=1,
即z=的取值范围为[0,1].
题型三 距离型线性规划问题
例1.(2018·太原模拟)已知实数x,y满足约束条件则z=x2+y2的取值范围为( )
A.[1,13] B.[1,4]
C. D.
【答案】 C
【解析】 不等式组表示的平面区域如图中阴影部分所示,由此得z=x2+y2的最小值为点O到直线BC:2x-y+2=0的距离的平方,=,最大值为点O与点A(-2,3)的距离的平方,=|OA|2=13.
例2.(2018·安庆二模)若实数x,y满足:|x|≤y≤1,则x2+y2+2x的最小值为( )
A. B.-
C. D.-1
【答案】B
【解析】 作出不等式|x|≤y≤1表示的可行域如图中阴影部分所示.
x2+y2+2x=(x+1)2+y2-1,(x+1)2+y2表示可行域内的点(x,y)到点(-1,0)距离的平方,由图可知,(x+1)2+y2的最小值为点(-1,0)到直线y=-x的距离的平方,即为=,
所以x2+y2+2x的最小值为-1=-.
题型四 线性规划中的含参问题
例1.当实数x,y满足时,1≤ax+y≤4恒成立,则实数a的取值范围是________.
【答案】
【解析】作出不等式组
表示的平面区域如图中阴影部分所示,
由1≤ax+y≤4恒成立,结合图可知,a≥0且在A(1,0)处取得最小值,在B(2,1)处取得最大值,所以a≥1,且2a+1≤4,故a的取值范围为.
例2.(2018·郑州质检)已知x,y满足约束条件,若目标函数z=3x+y的最大值为10,则z的最小值为________.
【答案】 5
【解析】画出不等式组表示的可行域如图中阴影部分所示,作直线l:3x+y=0,平移l,从而可知经过C点时z取到最大值,
由解得
∴2×3-1-m=0,m=5.
由图知,平移l经过B点时,z最小,
∴当x=2,y=2×2-5=-1时,z最小,=3×2-1=5.
例3.若不等式组解为坐标的点所表示的平面区域为三角形,且其面积为,则实数的值为( )
A. B. 1 C. 或1 D. 3或
【答案】B
【解析】做出不等式组对应的平面区域如图所示,若不等式组表示的平面区域为三角形,
由可得: ,即.
满足题意时,点位于直线下方,
即: ,解得: ,据此可排除ACD选项.
本题选择B选项.
题型五 利用基本不等式求最值
例1.(2018·常州调研)若实数x满足x>-4,则函数f(x)=x+的最小值为________.
【答案】2
【解析】∵x>-4,∴x+4>0,
∴f(x)=x+=x+4+-4≥2 -4=2,
当且仅当x+4=,即x=-1时取等号.
故f(x)=x+的最小值为2.
例2.正数a,b满足+=1,若不等式a+b≥-x2+4x+18-m对任意实数x恒成立,则实数m的取值范围是( )
A.[3,+∞) B.(-∞,3]
C.(-∞,6] D.[6,+∞)
【答案】D
【解析】 因为a>0,b>0,+=1,
所以a+b=(a+b)=10++≥10+2=16,
当且仅当=,即a=4,b=12时,等号成立.
由题意,得16≥-x2+4x+18-m,
即x2-4x-2≥-m对任意实数x恒成立,
令f(x)=x2-4x-2,
则f(x)=x2-4x-2=(x-2)2-6,
所以f(x)的最小值为-6,
所以-6≥-m,即m≥6.
成果巩固
题型一 截距型线性规划问题
1.(2018安阳市高三9月调研)若实数满足约束条件,则的最小值为 .
【答案】-28
【解析】画出不等式组表示的平面区域如图所示,由图知,当目标函数z=x+6y经过点A(-10,-3)时取得最小值,即z=-10+6×(-3)=-28.
2.(2018天津卷) 设变量x,y满足约束条件 则目标函数的最大值为( )
A. 6 B. 19 C. 21 D. 45
【答案】C
【解析】 绘制不等式组表示的平面区域如图所示,
结合目标函数的几何意义可知目标函数在点A处取得最大值,
联立直线方程:,可得点A的坐标为:,
据此可知目标函数的最大值为:.
本题选择C选项.
3. (2018北京卷)若x,y满足x+1≤ y ≤2x,则2y–x的最小值是__________.
【答案】3
4.(2018·成都模拟)某企业拟生产甲、乙两种产品,已知每件甲产品的利润为3万元,每件乙产品的利润为2万元,且甲、乙两种产品都需要在A,B两种设备上加工,在每台设备A,每台设备B上加工1件甲产品所需工时分别为1 h和2 h,加工1件乙产品所需工时分别为2 h和1 h,A设备每天使用时间不超过4 h,B设备每天使用时间不超过5 h,则通过合理安排生产计划,该企业在一天内的最大利润是 ( )
A.18万元 B.12万元
C.10万元 D.8万元
【答案】D
【解析】设每天生产甲、乙两种产品分别为x件,y件,企业获得的利润为z万元,
则x,y满足约束条件且z=3x+2y.
作出不等式组表示的可行域,
如图所示.由x∈N,y∈N可知最优解为(2,1),即生产甲产品2件,乙产品1件,可使企业获得最大利润,最大利润为8万元.
题型二 斜率型线性规划问题
1.(2018·郑州一中押题卷)若实数x,y满足约束条件则当取最大值时,x+y的值为( )
A.-1 B.1
C.- D.
【答案】D
【解析】 作出可行域如图中阴影部分所示,
的几何意义是过定点M(-3,-1)与可行域内的点(x,y)的直线的斜率,由图可知,当直线过点A(0,)时,斜率取得最大值,
此时x,y的值分别为0,,所以x+y=.
2.设变量,满足约束条件,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】所求可视为点与定点连线的斜率.
从而在可行域中寻找斜率的取值范围即可,
可得在处的斜率最小,即,
在处的斜率最大,为,
结合图像可得的范围为.故选D.
3.(2018·石家庄质检)若x,y满足约束条件则z=的最小值为( )
A.-2 B.- C.- D.
【答案】C
【解析】 作出不等式组表示的平面区域如图中阴影部分所示,
因为目标函数z=表示区域内的点与点P(-3,2)连线的斜率.
由图知当区域内的点与点P的连线与圆相切时斜率最小.
设切线方程为y-2=k(x+3),即,
则有=2,
解得k=-或k=0(舍去),所以=-,故选C.
题型三 距离型线性规划问题
1.若变量x,y满足约束条件则(x-2)2+y2的最小值为( )
A. B. C. D.5
【答案】D
【解析】 作出不等式组对应的平面区域如图中阴影部分所示.
设z=(x-2)2+y2,则z的几何意义为区域内的点到定点D(2,0)的距离的平方,由图知C,D间的距离最小,此时z最小.由得即C(0,1),
此时zmin=(x-2)2+y2=4+1=5,故选D.
2.已知圆C:(x-a)2+(y-b)2=1,平面区域:若圆心,且圆C与轴相切,则 a2+b2的最大值为 ( )
A.5 B.29
C.37 D.49
【答案】C
【解析】平面区域为如图所示的阴影部分,
因为圆心C(a,b)∈,且圆C与x轴相切,所以点C在如图所示的线段MN上,线段MN的方程为y=1(-2≤x≤6),由图形得,当点C在点N(6,1)处时,a2+b2取得最大值62+12=37,故选C.
3.若x,y满足约束条件则(x+2)2+(y+3)2的最小值为 ( )
A. 1 B. C. 5 D. 9
【答案】B
【解析】 不等式组表示的可行域如图阴影部分所示,由题意可知点P(-2,-3)到直线x+y+2=0的距离为=,所以(x+2)2+(y+3)2的最小值为=.
题型四 线性规划中的含参问题
1.当实数x,y满足时,ax+y≤4恒成立,则实数a的取值范围是________.[om]
【答案】
【解析】
由约束条件作可行域如图,联立,解得,
联立,解得,在中取得.
由得,要使恒成立,则平面区域在直线的下方,若,则不等式等价于,此时满足条件,若,即,平面区域满足条件,若,即时,
要使平面区域在直线的下方,则只要在直线上或直线下方即可,即,得,综上,所以实数的取值范围是.
2.已知实数, 满足条件若存在实数使得函数取到最大值的解有无数个,则_________, =_________.
【答案】 1
【解析】由约束条件画出可行域如下图, ,目标函数可化为
,取最大值即截距最大,且有无数个解,所以目标函数与边界重合,当,截距为最小值,不符,当时,符合。,填(1). (2). 1。
3.(2017·郑州第二次质量预测)已知直线y=k(x+1)与不等式组表示的平面区域有公共点,则k的取值范围为( )
A.[0,+∞) B.
C. D.
【答案】C
【解析】 画出不等式组表示的可行域如图中阴影(不含x轴)部分所示,直线y=k(x+1)过定点M(-1,0),
由解得过点M(-1,0)与A(1,3)的直线的斜率是,根据题意可知0
题型五 利用基本不等式求最值
1.若直线2mx-ny-2=0(m>0,n>0)过点(1,-2),则+的最小值为( )
A.2 B.6
C.12 D.3+2
【答案】D
【解析】 因为直线2mx-ny-2=0(m>0,n>0)过点(1,-2),
所以2m+2n-2=0,即m+n=1,
所以+=(m+n)=3++≥3+2,
当且仅当“=,即n=m”时取等号,
所以+的最小值为3+2,故选D.
2.(2018·河南百校联盟模拟)已知正实数a,b满足a+b=4,则+的最小值为________.
【答案】
【解析】∵a+b=4,∴a+1+b+3=8,∴+=[(a+1)+(b+3)]=≥×(2+2)=,当且仅当a+1=b+3,即a=3,b=1时取等号,∴+的最小值为.
3.(2018·湖南长郡中学月考)设正项等差数列{an}的前n项和为Sn,若S2 017=4 034,则+的最小值为________.
【答案】4
【解析】由等差数列的前n项和公式,得S2 017==4 034,则a1+a2 017=4.由等差数列的性质得a9+a2 009=4,所以+== +9 =≥ 2+10=4,当且仅当a2 009=3a9时等号成立,故所求最小值为4.
五、课堂小结
对于线性规划以画二元一次不等式(组)表示的平面区域、求目标函数最值为主,兼顾由最优解(可行域)情况确定参数的范围,以及简单线性规划问题的实际应用,加强转化与化归和数形结合思想的应用意识.理解基本不等式成立的条件,会利用基本不等式求最值.常与函数、解析几何、不等式相结合考查,加强数形结合、分类讨论、转化与化归等数学思想的应用意识.基本不等式作为求最值的方法,常在函数、解析几何、不等式的解答题中考查,难度中档.
一、高考回顾
不等式是高中数学的重要内容,它渗透到了中学数学的很多章节,在实际问题中被广泛应用,可以说是解决其它数学问题的一种有效工具.不等式是高考数学命题的重要内容之一,其核心考点为线性规划(高频)、不等式的性质与证明、不等式的解法(高频)和不等式的应用(利用不等式求最值(高频)).借助可行域与目标函数、不等式的基本性质,考查函数方程思想、等价转化思想、数形结合思想及分类讨论思想等数学思想方法.含参数不等式的解法与讨论,不等式与函数、数列、三角等内容的综合问题,仍是高考命题的热点.
知识清单
1.思维导图
(
核心方法
思维特征
动直线(
x,y
)
最值
不等式及其解法
简单的线性规划
基本不等式
核心知识
不等式
数形结合
分类讨论
函数与方程
图象语言
符号化语言
描述性语言
思维载体
)
2.知识再现
1.二元一次不等式表示的平面区域
(1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.我们把直线画成虚线,以表示区域不包括边界直线.当我们在坐标系中画不等式Ax+By+C≥0所表示的平面区域时,此区域应包括边界直线,则把边界直线画成实线.
(2)对于直线Ax+By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+By+C,所得的符号都相同,所以只需在此直线的同一侧取一个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号即可断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
2.线性规划相关概念
名称 意义
约束条件 由变量x,y组成的一次不等式
线性约束条件 由x,y的一次不等式(或方程)组成的不等式组
目标函数 欲求最大值或最小值的函数
线性目标函数 关于x,y的一次解析式
可行解 满足线性约束条件的解
可行域 所有可行解组成的集合
最优解 使目标函数取得最大值或最小值的可行解
线性规划问题 在线性约束条件下求线性目标函数的最大值或最小值问题
3.基本不等式:≤
(1)基本不等式成立的条件:a>0,b>0.
(2)等号成立的条件:当且仅当a=b时取等号.
4. 几个重要的不等式
(1)a2+b2≥2ab(a,b∈R).
(2)+≥2(a,b同号).
(3)ab≤(a,b∈R).
(4)≥ (a,b∈R).
以上不等式等号成立的条件均为a=b.
5. 算术平均数与几何平均数
设a>0,b>0,则a,b的算术平均数为,几何平均数为,基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数.
6.利用基本不等式求最值问题
已知x>0,y>0,则
(1)如果积是定值p,那么当且仅当x=y时,x+y有最小值2.(简记:积定和最小)
(2)如果和x+y是定值p,那么当且仅当x=y时,有最大值.(简记:和定积最大)
三、例题精讲
题型一 截距型线性规划问题
例1.(2018全国1).若,满足约束条件,则的最大值为_______________.
【答案】 6.
【解析】画出可行域如图所示,可知目标函数过点时取得最大值,.
例2.(2018·西安质检)若变量x,y满足则2x+y的取值范围为________.
【答案】[-2,2]
【解析】作出满足不等式组的平面区域如图中阴影部分所示,
平移直线2x+y=0,经过点A(1,0)时,2x+y取得最大值2×1+0=2,
经过点B(-1,0)时,2x+y取得最小值2×(-1)+0=-2,
所以2x+y的取值范围为[-2,2].
例3. (2018·黄冈联考)一个小型加工厂用一台机器生产甲、乙两种桶装饮料,生产一桶甲饮料需要白糖4千克,果汁18千克,用时3小时;生产一桶乙饮料需要白糖1千克,果汁15千克,用时1小时.现库存白糖10千克,果汁66千克,生产一桶甲饮料利润为200元,生产一桶乙饮料利润为100元,在使用该机器用时不超过9小时的条件下,生产甲、乙两种饮料利润之和的最大值为________.
【答案】 600
【解析】 设生产甲、乙两种饮料分别为x桶、y桶,利润为z元,
则得即
目标函数z=200x+100y.作出可行域(如图阴影部分所示),当直线z=200x+100y经过可行域上点B时,z取得最大值,解方程组得点B的坐标(2,2),故=200×2+100×2=600.
题型二 斜率型线性规划问题
例1.(2018·成都一诊)若实数x,y满足约束条件则的最小值为________.
【答案】-
【解析】作出不等式组表示的平面区域如图中阴影部分所示,
因为表示平面区域内的点与定点P(0,1)连线的斜率.
由图知,点P与点A连线的斜率最小,
所以min===-.
例2.已知实数,满足约束条件,则的取值范围为( )
A. B.
C. D.
【答案】 C
【解析】画出不等式表示的可行域,如图阴影三角形所示,
由题意得,.
由得,
所以可看作点和连线的斜率,记为,
由图形可得,
又,,所以,
因此或,所以的取值范围为.故选C.
例3.(2018·安徽江南十校联考)已知实数x,y满足,则z=的取值范围为________.
【答案】[0,1].
【解析】 作出不等式组对应的平面区域,如图阴影部分.z=表示区域内的点(x,y)与A(0,-1)连线的斜率k,由图可知,=0,,P为切点,设,=,
∴=,∴x0=1,=1,
即z=的取值范围为[0,1].
题型三 距离型线性规划问题
例1.(2018·太原模拟)已知实数x,y满足约束条件则z=x2+y2的取值范围为( )
A.[1,13] B.[1,4]
C. D.
【答案】 C
【解析】 不等式组表示的平面区域如图中阴影部分所示,由此得z=x2+y2的最小值为点O到直线BC:2x-y+2=0的距离的平方,=,最大值为点O与点A(-2,3)的距离的平方,=|OA|2=13.
例2.(2018·安庆二模)若实数x,y满足:|x|≤y≤1,则x2+y2+2x的最小值为( )
A. B.-
C. D.-1
【答案】B
【解析】 作出不等式|x|≤y≤1表示的可行域如图中阴影部分所示.
x2+y2+2x=(x+1)2+y2-1,(x+1)2+y2表示可行域内的点(x,y)到点(-1,0)距离的平方,由图可知,(x+1)2+y2的最小值为点(-1,0)到直线y=-x的距离的平方,即为=,
所以x2+y2+2x的最小值为-1=-.
题型四 线性规划中的含参问题
例1.当实数x,y满足时,1≤ax+y≤4恒成立,则实数a的取值范围是________.
【答案】
【解析】作出不等式组
表示的平面区域如图中阴影部分所示,
由1≤ax+y≤4恒成立,结合图可知,a≥0且在A(1,0)处取得最小值,在B(2,1)处取得最大值,所以a≥1,且2a+1≤4,故a的取值范围为.
例2.(2018·郑州质检)已知x,y满足约束条件,若目标函数z=3x+y的最大值为10,则z的最小值为________.
【答案】 5
【解析】画出不等式组表示的可行域如图中阴影部分所示,作直线l:3x+y=0,平移l,从而可知经过C点时z取到最大值,
由解得
∴2×3-1-m=0,m=5.
由图知,平移l经过B点时,z最小,
∴当x=2,y=2×2-5=-1时,z最小,=3×2-1=5.
例3.若不等式组解为坐标的点所表示的平面区域为三角形,且其面积为,则实数的值为( )
A. B. 1 C. 或1 D. 3或
【答案】B
【解析】做出不等式组对应的平面区域如图所示,若不等式组表示的平面区域为三角形,
由可得: ,即.
满足题意时,点位于直线下方,
即: ,解得: ,据此可排除ACD选项.
本题选择B选项.
题型五 利用基本不等式求最值
例1.(2018·常州调研)若实数x满足x>-4,则函数f(x)=x+的最小值为________.
【答案】2
【解析】∵x>-4,∴x+4>0,
∴f(x)=x+=x+4+-4≥2 -4=2,
当且仅当x+4=,即x=-1时取等号.
故f(x)=x+的最小值为2.
例2.正数a,b满足+=1,若不等式a+b≥-x2+4x+18-m对任意实数x恒成立,则实数m的取值范围是( )
A.[3,+∞) B.(-∞,3]
C.(-∞,6] D.[6,+∞)
【答案】D
【解析】 因为a>0,b>0,+=1,
所以a+b=(a+b)=10++≥10+2=16,
当且仅当=,即a=4,b=12时,等号成立.
由题意,得16≥-x2+4x+18-m,
即x2-4x-2≥-m对任意实数x恒成立,
令f(x)=x2-4x-2,
则f(x)=x2-4x-2=(x-2)2-6,
所以f(x)的最小值为-6,
所以-6≥-m,即m≥6.
成果巩固
题型一 截距型线性规划问题
1.(2018安阳市高三9月调研)若实数满足约束条件,则的最小值为 .
【答案】-28
【解析】画出不等式组表示的平面区域如图所示,由图知,当目标函数z=x+6y经过点A(-10,-3)时取得最小值,即z=-10+6×(-3)=-28.
2.(2018天津卷) 设变量x,y满足约束条件 则目标函数的最大值为( )
A. 6 B. 19 C. 21 D. 45
【答案】C
【解析】 绘制不等式组表示的平面区域如图所示,
结合目标函数的几何意义可知目标函数在点A处取得最大值,
联立直线方程:,可得点A的坐标为:,
据此可知目标函数的最大值为:.
本题选择C选项.
3. (2018北京卷)若x,y满足x+1≤ y ≤2x,则2y–x的最小值是__________.
【答案】3
4.(2018·成都模拟)某企业拟生产甲、乙两种产品,已知每件甲产品的利润为3万元,每件乙产品的利润为2万元,且甲、乙两种产品都需要在A,B两种设备上加工,在每台设备A,每台设备B上加工1件甲产品所需工时分别为1 h和2 h,加工1件乙产品所需工时分别为2 h和1 h,A设备每天使用时间不超过4 h,B设备每天使用时间不超过5 h,则通过合理安排生产计划,该企业在一天内的最大利润是 ( )
A.18万元 B.12万元
C.10万元 D.8万元
【答案】D
【解析】设每天生产甲、乙两种产品分别为x件,y件,企业获得的利润为z万元,
则x,y满足约束条件且z=3x+2y.
作出不等式组表示的可行域,
如图所示.由x∈N,y∈N可知最优解为(2,1),即生产甲产品2件,乙产品1件,可使企业获得最大利润,最大利润为8万元.
题型二 斜率型线性规划问题
1.(2018·郑州一中押题卷)若实数x,y满足约束条件则当取最大值时,x+y的值为( )
A.-1 B.1
C.- D.
【答案】D
【解析】 作出可行域如图中阴影部分所示,
的几何意义是过定点M(-3,-1)与可行域内的点(x,y)的直线的斜率,由图可知,当直线过点A(0,)时,斜率取得最大值,
此时x,y的值分别为0,,所以x+y=.
2.设变量,满足约束条件,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】所求可视为点与定点连线的斜率.
从而在可行域中寻找斜率的取值范围即可,
可得在处的斜率最小,即,
在处的斜率最大,为,
结合图像可得的范围为.故选D.
3.(2018·石家庄质检)若x,y满足约束条件则z=的最小值为( )
A.-2 B.- C.- D.
【答案】C
【解析】 作出不等式组表示的平面区域如图中阴影部分所示,
因为目标函数z=表示区域内的点与点P(-3,2)连线的斜率.
由图知当区域内的点与点P的连线与圆相切时斜率最小.
设切线方程为y-2=k(x+3),即,
则有=2,
解得k=-或k=0(舍去),所以=-,故选C.
题型三 距离型线性规划问题
1.若变量x,y满足约束条件则(x-2)2+y2的最小值为( )
A. B. C. D.5
【答案】D
【解析】 作出不等式组对应的平面区域如图中阴影部分所示.
设z=(x-2)2+y2,则z的几何意义为区域内的点到定点D(2,0)的距离的平方,由图知C,D间的距离最小,此时z最小.由得即C(0,1),
此时zmin=(x-2)2+y2=4+1=5,故选D.
2.已知圆C:(x-a)2+(y-b)2=1,平面区域:若圆心,且圆C与轴相切,则 a2+b2的最大值为 ( )
A.5 B.29
C.37 D.49
【答案】C
【解析】平面区域为如图所示的阴影部分,
因为圆心C(a,b)∈,且圆C与x轴相切,所以点C在如图所示的线段MN上,线段MN的方程为y=1(-2≤x≤6),由图形得,当点C在点N(6,1)处时,a2+b2取得最大值62+12=37,故选C.
3.若x,y满足约束条件则(x+2)2+(y+3)2的最小值为 ( )
A. 1 B. C. 5 D. 9
【答案】B
【解析】 不等式组表示的可行域如图阴影部分所示,由题意可知点P(-2,-3)到直线x+y+2=0的距离为=,所以(x+2)2+(y+3)2的最小值为=.
题型四 线性规划中的含参问题
1.当实数x,y满足时,ax+y≤4恒成立,则实数a的取值范围是________.[om]
【答案】
【解析】
由约束条件作可行域如图,联立,解得,
联立,解得,在中取得.
由得,要使恒成立,则平面区域在直线的下方,若,则不等式等价于,此时满足条件,若,即,平面区域满足条件,若,即时,
要使平面区域在直线的下方,则只要在直线上或直线下方即可,即,得,综上,所以实数的取值范围是.
2.已知实数, 满足条件若存在实数使得函数取到最大值的解有无数个,则_________, =_________.
【答案】 1
【解析】由约束条件画出可行域如下图, ,目标函数可化为
,取最大值即截距最大,且有无数个解,所以目标函数与边界重合,当,截距为最小值,不符,当时,符合。,填(1). (2). 1。
3.(2017·郑州第二次质量预测)已知直线y=k(x+1)与不等式组表示的平面区域有公共点,则k的取值范围为( )
A.[0,+∞) B.
C. D.
【答案】C
【解析】 画出不等式组表示的可行域如图中阴影(不含x轴)部分所示,直线y=k(x+1)过定点M(-1,0),
由解得过点M(-1,0)与A(1,3)的直线的斜率是,根据题意可知0
题型五 利用基本不等式求最值
1.若直线2mx-ny-2=0(m>0,n>0)过点(1,-2),则+的最小值为( )
A.2 B.6
C.12 D.3+2
【答案】D
【解析】 因为直线2mx-ny-2=0(m>0,n>0)过点(1,-2),
所以2m+2n-2=0,即m+n=1,
所以+=(m+n)=3++≥3+2,
当且仅当“=,即n=m”时取等号,
所以+的最小值为3+2,故选D.
2.(2018·河南百校联盟模拟)已知正实数a,b满足a+b=4,则+的最小值为________.
【答案】
【解析】∵a+b=4,∴a+1+b+3=8,∴+=[(a+1)+(b+3)]=≥×(2+2)=,当且仅当a+1=b+3,即a=3,b=1时取等号,∴+的最小值为.
3.(2018·湖南长郡中学月考)设正项等差数列{an}的前n项和为Sn,若S2 017=4 034,则+的最小值为________.
【答案】4
【解析】由等差数列的前n项和公式,得S2 017==4 034,则a1+a2 017=4.由等差数列的性质得a9+a2 009=4,所以+== +9 =≥ 2+10=4,当且仅当a2 009=3a9时等号成立,故所求最小值为4.
五、课堂小结
对于线性规划以画二元一次不等式(组)表示的平面区域、求目标函数最值为主,兼顾由最优解(可行域)情况确定参数的范围,以及简单线性规划问题的实际应用,加强转化与化归和数形结合思想的应用意识.理解基本不等式成立的条件,会利用基本不等式求最值.常与函数、解析几何、不等式相结合考查,加强数形结合、分类讨论、转化与化归等数学思想的应用意识.基本不等式作为求最值的方法,常在函数、解析几何、不等式的解答题中考查,难度中档.
同课章节目录
