2019年高考三轮冲刺振动与波动 光及光的本质 Word版含解析
文档属性
| 名称 | 2019年高考三轮冲刺振动与波动 光及光的本质 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 429.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-05-03 00:00:00 | ||
图片预览



文档简介
2019年高考三轮冲刺振动与波动 光及光的本质
教材版本 全国通用 课时说明 120分钟
知识点 简谐运动 机械波的形成和传播特点 波的图像 波的特性 波的多解 光的折射、全反射
复习目标 1.能够区分振动图像和波动图像 2.会计算波的多解问题 3、掌握光的折射定律和全反射
复习重点 振动图像和波动图像、光的折射定律和全反射
复习难点 波的多解问题、光的折射定律和全反射
一、高考回顾
1.(2017,全国卷3)如图所示一列简谐横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5s时的波形图.已知该简谐波的周期大于0.5s.关于该简谐波,下列说法正确的是( )
图15-g1-1
A.波长为2m
B.波速为6m/s
C.频率为1.5Hz
D.t=1s时,x=1m处的质点处于波峰
E.t=2s时,x=2m处的质点经过平衡位置
【答案】BCE
【解析】A错:由简谐波的波动图象可知,波长为4m.
B对:t=0.5s时波向x轴正方向传播的距离为x=λ(n=0,1,2,3…),即t=T=0.5s(n=0,1,2,3…),又T>0.5s,解之得T=,当n=0时,T=s,符合题意;当n=1时,T=s<0.5 s,不符合题意,则波速v==6 m/s.
C对:频率f==1.5Hz.
D错:t=0时x=1m处的质点处于波峰,因t=1s时n===1.5,则此时x=1m处的质点处于波谷.
E对:t=0时x=2m处的质点经过平衡位置向上振动,因t=2s时n===3,则此时x=2m处的质点经过平衡位置向上振动.
2.(2016,全国卷3)由波源S形成的简谐横波在均匀介质中向左、右传播.波源振动的频率为20Hz,波速为16m/s.已知介质中P、Q两质点位于波源S的两侧,且P、Q和S的平衡位置在一条直线上,P、Q的平衡位置到S的平衡位置之间的距离分别为15.8m、14.6m.P、Q开始振动后,下列判断正确的是( )
A.P、Q两质点运动的方向始终相同
B.P、Q两质点运动的方向始终相反
C.当S恰好通过平衡位置时,P、Q两点也正好通过平衡位置
D.当S恰好通过平衡位置向上运动时,P在波峰
E.当S恰好通过平衡位置向下运动时,Q在波峰
【答案】BDE
【解析】简谐横波的波长λ== m=0.8m.P、Q两质点距离波源S的距离PS=15.8m=19λ+λ,SQ=14.6m=18λ+λ.因此P、Q两质点运动的方向始终相反,A错误,B正确.当S恰好通过平衡位置向上运动时,P在波峰的位置,Q在波谷的位置.当S恰好通过平衡位置向下运动时,P在波谷的位置,Q在波峰的位置.C错误,D、E正确.
3.(2018,天津卷) 一振子沿x轴做简谐运动,平衡位置在坐标原点。t=0时振子的位移为-0.1m,t=1s时位移为0.1m,则( )
A. 若振幅为0.1m,振子的周期可能为
B. 若振幅为0.1m,振子的周期可能为
C. 若振幅为0.2m,振子的周期可能为4s
D. 若振幅为0.2m,振子的周期可能为6s
【答案】AD
【解析】t=0时刻振子的位移x=-0.1m,t=1s时刻x=0.1m,关于平衡位置对称;如果振幅为0.1m,则1s为半周期的奇数倍;如果振幅为0.2m,分靠近平衡位置和远离平衡位置分析.若振幅为0.1m,根据题意可知从t=0s到t=1s振子经历的周期为,则,解,当n=1时,无论n为何值,T都不会等于,A正确B错误;如果振幅为0.2m,结合位移时间关系图象,有①,或者②,或者③,对于①式,只有当n=0时,T=2s,为整数;对于②式,T不为整数;对于③式,当n=0时,T=6s,之后只会大于6s,故C错误D正确
【点睛】t=0时刻振子的位移x=-0.1m,t=1s时刻x=0.1m,关于平衡位置对称;如果振幅为0.1m,则1s为半周期的奇数倍;如果振幅为0.2m,分靠近平衡位置和远离平衡位置分析.
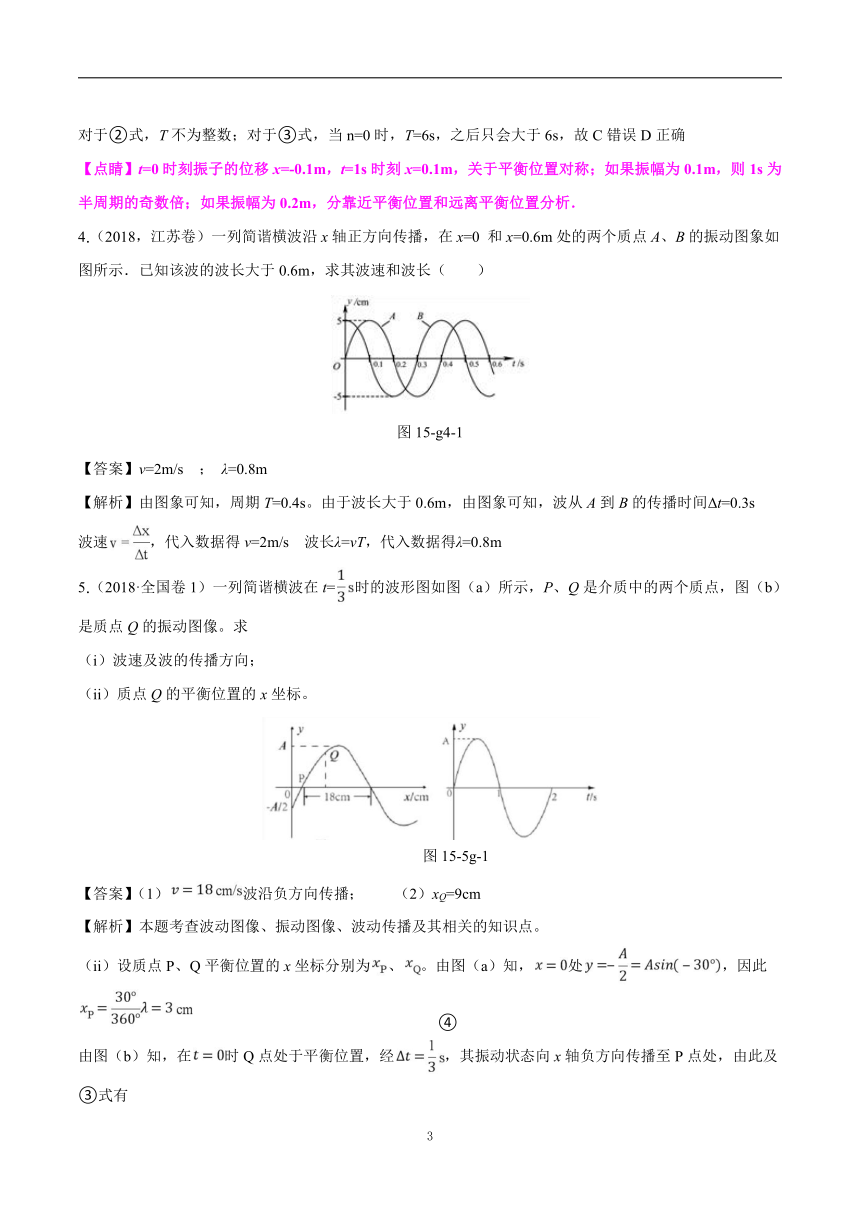
4.(2018,江苏卷)一列简谐横波沿x轴正方向传播,在x=0 和x=0.6m处的两个质点A、B的振动图象如图所示.已知该波的波长大于0.6m,求其波速和波长( )
图15-g4-1
【答案】v=2m/s ; λ=0.8m
【解析】由图象可知,周期T=0.4s。由于波长大于0.6m,由图象可知,波从A到B的传播时间Δt=0.3s
波速,代入数据得v=2m/s 波长λ=vT,代入数据得λ=0.8m
5.(2018·全国卷1)一列简谐横波在t=时的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图像。求
(i)波速及波的传播方向;
(ii)质点Q的平衡位置的x坐标。
图15-5g-1
【答案】(1)波沿负方向传播; (2)xQ=9cm
【解析】本题考查波动图像、振动图像、波动传播及其相关的知识点。
(ii)设质点P、Q平衡位置的x坐标分别为、。由图(a)知,处,因此
④
由图(b)知,在时Q点处于平衡位置,经,其振动状态向x轴负方向传播至P点处,由此及③式有
⑤
由④⑤式得,质点Q的平衡位置的x坐标为xQ=9 cm
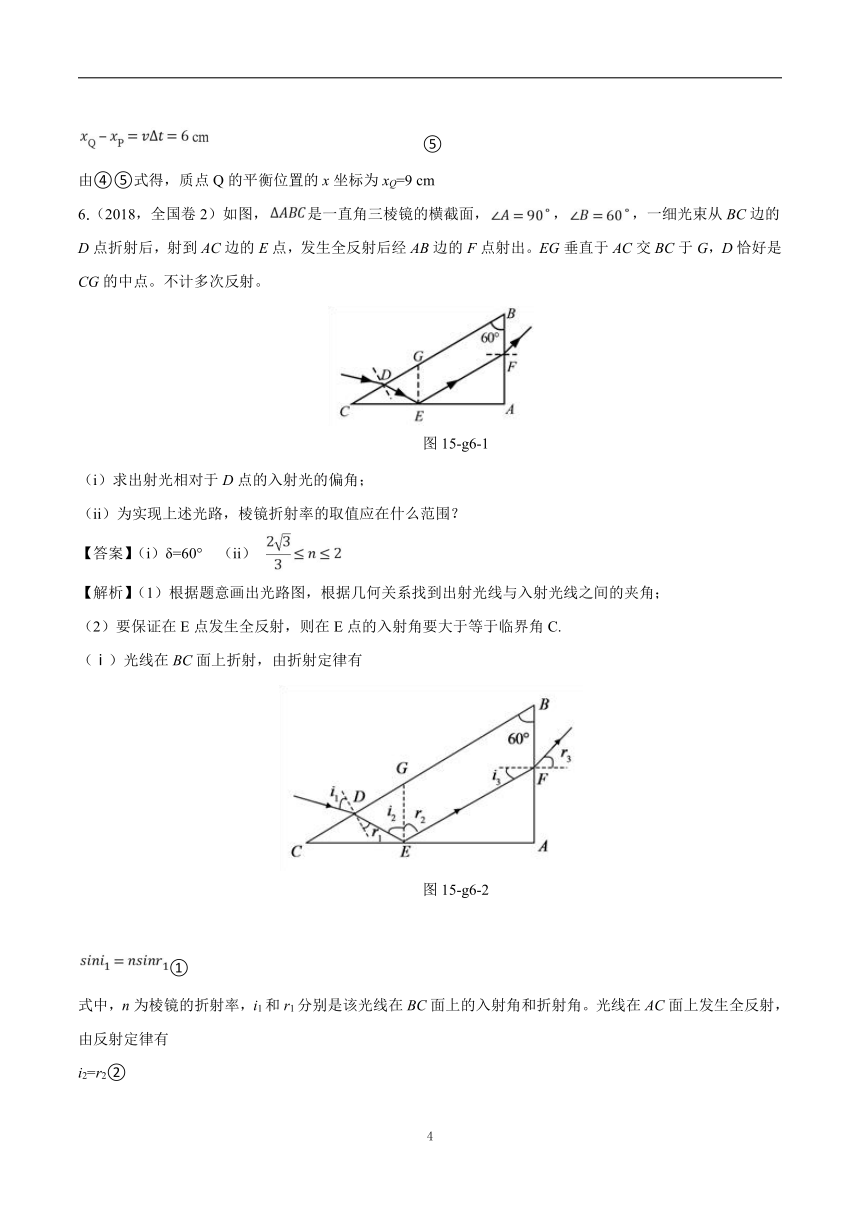
6.(2018,全国卷2)如图,是一直角三棱镜的横截面,,,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
图15-g6-1
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
【答案】(i)δ=60° (ii)
【解析】(1)根据题意画出光路图,根据几何关系找到出射光线与入射光线之间的夹角;
(2)要保证在E点发生全反射,则在E点的入射角要大于等于临界角C.
(ⅰ)光线在BC面上折射,由折射定律有
图15-g6-2
①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角。光线在AC面上发生全反射,由反射定律有
i2=r2②
式中i2和r2分别是该光线在AC面上的入射角和反射角。光线在AB面上发生折射,由折射定律有
③
式中i3和r3分别是该光线在AB面上的入射角和折射角。由几何关系得
i2=r2=60°,r1=i3=30°④
F点的出射光相对于D点的入射光的偏角为
δ=(r1–i1)+(180°–i2–r2)+(r3–i3)⑤
由①②③④⑤式得
δ=60°⑥
(ⅱ)光线在AC面上发生全反射,光线在AB面上不发生全反射,有
⑦
式中C是全反射临界角,满足
⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为
⑨
故本题答案是:(i)δ=60° (ii)
【点睛】本题考查了几何光学,处理此类题的方法一般是正确画光路图利用几何关系求偏角,还要知道全发射的条件是什么。
7.(2018·全国卷3)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察。恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2cm,EF=1cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
图15-g7-1
【答案】
【解析】本题考查折射定律、光在三棱镜中传播及其相关的知识点。
过D点作AB边的发现,连接OD,则为O点发出的光纤在D点的入射角;设该光线在D点的折射角为β,如图所示。根据折射定律有
图15-g7-2
①
式中n为三棱镜的折射率
由几何关系可知
②
③
在中有
④
由③④式和题给条件得
⑤
根据题给条件可知,为等腰三角形,有
⑥
由①②⑥式得
⑦
二、知识清单
(
机械振动
简谐运动
物体在跟偏离平衡位置的位移大小成正比,且总是指向平衡位置的回复力作用下的振动,叫做简谐振动。也称为无阻尼振动或等幅振动。
特征
:振幅保持不变的自由振动。
描述量
:振幅
A
,周期
T
,频率
f
=
1/T
。
x-t
图像
:正弦曲线或余弦曲线
振动能
:动能和势能之和,机械能守恒
相关物理量的周期性变化
:位移、回复力、即时速度、即时加速度,动能与势能等。
受力特征:回
复力
F
=-
kx
=-
mω
2
x
基本模型:①
单摆(
θ<10°
):
②
弹簧振子:
,
;
;
衍射
波传播过程中遇到孔和障碍物时,绕过孔和障碍物的现象叫波的衍射。发生明显衍射的条件是孔、障碍物的尺寸与波长可比拟。
衍射是波特有的现象。
干涉
波的叠加
:两列波重叠区域,任何一点的位移等于两列波引起的位移的矢量和。
二列频率相同、振动方向相同的波相遇,使媒质中有的地方振动加强,有的地方振动减弱,且加强与减弱部分相间隔的现象叫波的干涉。
干涉是波特有的现象。
干涉区域内某点是振动最强点还是振动最弱点的充要条件
:
①最强:该点到两个波源的路程之差是波长的整数倍,即
δ=nλ
②最弱:该点到两个波源的路程之差是半波长的奇数倍,即
δ=
(2
n
+1)
λ
/2
机械波
振动在媒质中传播形成波;媒质各点都在各自平衡位置附近振动但不随波形一起迁移,波是能量传递的一种形式。
描述量
:波幅
A
,波长λ,波速
V
,周期
T
,频率
f
。
描述公式
:
V=
λ
/
T
=
λf
;
波速大小由传播振动的介质特性所决定;波的频率等于质点振动频率,大小由振源决定,与介质无关;波长由波源和介质决定
波的图像:
表述了某一时刻各个质点偏离平衡位置的状况。为正弦曲线或余弦曲线(与振动图像很相似,但是有本质区别)
波的类型
:横波和纵波。
波的例子:声波(超声波、次声波、可听声波
20-20000Hz
)
阻尼振动
定义:
振幅逐渐减小的自由振动叫阻尼振动。
特征:
振幅递减
原因
:振动能逐渐转化为其他形式的能。
自由振动
受迫振动
受迫振动
定义
:
物体在周期性外力(驱动力)作用下的振动叫受迫振动。
特征
:受迫振动稳定后的频率等于驱动的频率;而当驱动力的频率接近振动物体的固有频率时,受迫振动振幅增大的现象叫
共振
。
机械波
波的特性
:
波的叠加原理:各列波彼此通过,互不干扰;介质质点位移等于各位移的矢量和
波的特有现象:
波的衍射
绕过障碍物或孔继续传播的现象
波的干涉
两列波在相遇的区域内叠加形式的一种现象
特殊现象:多普勒效应
波的形成条件
波源和介质
波的形成原因
介质质点之间有相互作用
波的实质
传递振动的形式、能量和信息,质点并不随着波动而迁移;
后一质点的振动滞后于前一质点,且重复前一质点的振动;
每个质点的的起振方向是相同的。
多普勒效应
波源与观察者之间有相对运动时,观察者感到频率发生变化的现象。
波源与观察者相互靠近时,观察者接收到的频率增大
)
三、例题精讲
例1一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,质点P的x坐标为3m.已知任意振动质点连续2次经过平衡位置的时间间隔为0.4s.下列说法正确的是( )
图15?L1?1
A.波速为4 m/s
B.波的频率为1.25 Hz
C.x坐标为15 m的质点在t=0.6 s时恰好位于波谷
D.x坐标为22 m的质点在t=0.2 s时恰好位于波峰
E.当质点P位于波峰时,x坐标为17 m的质点恰好位于波谷
【答案】BDE
【解析】任意振动质点连续2次经过平衡位置的时间间隔为0.4s,则T=0.4s,解得T=0.8s.从图象中可知λ=4m,所以根据公式v==5m/s,故A错误;根据公式f=可得波的频率为1.25Hz,B正确;x坐标为15m的质点和x坐标为3m的质点相隔12m,为波长的整数倍,即两质点为同相点,而x坐标为3m的质点经过t=0.6s即四分之三周期振动到平衡位置,所以x坐标为15m的质点在t=0.6s时振动到平衡位置,C错误;x的坐标为22m的质点和x的坐标为2m的质点为同相点,x的坐标为2m的质点经过t=0.2s即四分之一周期恰好位于波峰,故x的坐标为22m的质点在t=0.2 s时恰好位于波峰,D正确;x坐标为17m的质点和x坐标为1m的质点为同相点,当质点P位于波峰时,坐标为1m的质点恰好位于波谷,E正确.
【易错点】 波的传播方向与质点振动方向的互判方法
例2一列简谐横波,在t=0.6 s时刻的图象如图15?L2?1甲所示,此时,P、Q两质点的位移均为-1 cm,波上A质点的振动图象如图乙所示,则以下说法正确的是( )
甲 乙
图15?L2?1
A.这列波沿x轴正方向传播
B.这列波的波速是m/s
C.从t=0.6s开始,紧接着的Δt=0.6s时间内,A质点通过的路程是10m
D.从t=0.6s开始,质点P比质点Q早0.4s回到平衡位置
E.若该波在传播过程中遇到一个尺寸为10m的障碍物不能发生明显衍射现象
【答案】ABD
【解析】由图乙读出t=0.6 s时刻质点A的速度方向沿y轴负方向,由图甲判断出波的传播方向为x轴正方向,A正确;由图甲读出该波的波长为λ=20 m,由图乙知周期为T=1.2 s,则波速为v==m/s= m/s,B正确;Δt=0.6 s=0.5T ,质点做简谐运动时,在一个周期内质点A通过的路程是4倍振幅,则经过Δt=0.6 s,A质点通过的路程是s=2A=2×2 cm=4 cm,C错误;图甲中图示时刻质点P沿y轴正方向运动,质点Q沿y轴负方向运动,所以质点P比质点Q早回到平衡位置,由图甲知,P与Q的相位差Δφ=π,相差时间Δt′=T=0.4 s,D正确;发生明显衍射现象的条件是障碍物比波长的尺寸小或相差不多,由于障碍物的尺寸为10 m,小于波长20 m,E错误.
【易错点】(1)分清振动图象与波动图象.
(2)看清横、纵坐标的单位.尤其要注意单位前的数量级.
(3)找准波动图象对应的时刻.
(4)找准振动图象对应的质点.
例3如图所示,实线是某时刻的波形图,虚线是0.2s后的波形图.
图15?L3?1
(1)若波向左传播,求它的可能周期和最大周期;
(2)若波向右传播,求它可能的传播速度.
【答案】(1)(n=0,1,2,…) 0.27s (2)5(4n+1)m/s(n=0,1,2,…)
【解析】(1)波向左传播,传播的时间为
Δt=T+nT(n=0,1,2,…)
所以T==4× s= s(n=0,1,2,…)
最大周期为Tm= s≈0.27s.
(2)波向右传播,Δt=+nT(n=0,1,2,…)
T=s(n=0,1,2,…)
而λ=4m,所以v==5(4n+1)m/s(n=0,1,2,…).
【易错点】(1)根据初、末两时刻的波形图确定传播距离与波长的关系通式.
(2)根据题设条件判断是唯一解还是多解.
(3)根据波速公式求波速.
例4如图15?L4?1所示是水面上两列频率相同的波在某时刻的叠加情况,以波源S1、S2为圆心的两组同心圆弧分别表示同一时刻两列波的波峰(实线)和波谷(虚线).S1的振幅A1=4 cm,S2的振幅A2=3 cm,则下列说法正确的是( )
图15?L4?1
A.质点D是振动减弱点
B.质点A、D在该时刻的高度差为14 cm
C.再过半个周期,质点B、C是振动加强点
D.质点C的振幅为1 cm
E.质点C此刻以后将向下振动
【答案】BDE
【解析】由图象可知,D点为两波谷相遇,应该是加强点,选项A错误;此时A点在加强后的最高点,D点在加强后的最低点,由波的叠加可知AD的高度差为14 cm,选项B正确;由于两波的频率相等,叠加后会形成稳定的干涉图象,所以A、D点始终是加强点,B、C点始终是减弱点,选项C错误;质点C为减弱点,振幅为两振幅之差,为1 cm,选项D正确;由题意可知此时刻以后质点C将向下振动,选项E正确.
【易错点】波的干涉现象中加强点、减弱点的判断方法
图象法:在某时刻波的干涉的波形图上,波峰与波峰(或波谷与波谷)的交点,一定是加强点,而波峰与波谷的交点一定是减弱点,各加强点或减弱点各自连接而成以两波源为中心向外辐射的连线,形成加强线和减弱线.
例5如图15?L5?1所示,一束平行光垂直射到等腰三角形棱镜的底面上,三角形棱镜底角为α,底边长为3 cm,在三棱镜下面距棱镜底面L=10 cm处有一光屏,在光屏中央形成宽为2d=2.4 cm的暗斑.已知该棱镜对该光的折射率n=,sin 15°=,cos 15°=,tan 15°=0.27.
图15?L5?1
(1)求棱镜的底角α;
(2)光屏至少向上移动多长距离暗斑将消失?(结果保留两位有效数字)
【答案】(1)30° (2)4.4 cm
【解析】(1)作出这束平行光经过棱镜后的光路图如图所示.
图15?L5?2
设折射光线与入射光线的夹角为θ,从图中可看出光在棱镜的斜边上折射时,入射角为α,折射角为θ+α
由折射定律可得n==
由图知tan θ==0.27,所以θ=15°
代入解得α=30°.
(2)将光屏移到两边界折射光线交点时屏上暗斑将消失设光屏距两边界折射光线的交点为L1
由几何知识得L1=
解得L1=4.4 cm
光屏至少向上移动4.4 cm时,暗斑将消失.
【易错点】光的折射定律和全反射
四、思维点拨
重点突破 1 波的传播方向与质点振动方向的互判方法
内容 图象
“上下坡”法 沿波的传播方向,“上坡”时质点向下振动,“下坡”时质点向上振动
“同侧”法 波形图上某点表示传播方向和振动方向的箭头在图线同侧
“微平移”法 将波形沿传播方向进行微小的平移,再由对应同一x坐标的两波形曲线上的点来判断振动方向
重点突破2 求解波的多解问题的一般步骤
(1)根据初、末两时刻的波形图确定传播距离与波长的关系通式.
(2)根据题设条件判断是唯一解还是多解.
(3)根据波速公式求波速.
重点突破3 光的色散
1.光的色散成因
棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象.
光线通过棱镜的光路
2.各种色光的比较
颜色 红 橙 黄 绿 青 蓝 紫
频率ν 低―→高
同一介质中的折射率 小―→大
同一介质中的速度 大―→小
波长 大―→小
通过棱镜的偏折角 小―→大
临界角 大―→小
双缝干涉时的条纹间距 大―→小
五、成果巩固
【基础达标】
1. (2018·宝鸡模拟)如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5 m处开始计时.已知x=1 m处的质点P连续两次位于波峰的时间间隔为0.4 s,则下面说法中正确的是( )
图15?1?1
A.该列波在0.1 s内向右传播的距离为1 m
B.质点P(x=1 m)在0.1 s内向右运动的位移大小为1 m
C.在0~0.1 s时间内,质点Q(x=1.5 m)通过的路程是10 cm
D.在t=0.2 s时,质点Q(x=1.5 m)的振动方向沿y轴正方向
E.质点N(x=9 m)经过0.5 s第一次到达波谷
【答案】ADE
【解析】T=0.4 s,v==10 m/s,该列波在0.1 s内向右传播的距离为x=10×0.1 m=1 m,A正确;质点不会随波迁移,B错误;质点Q在0~0.1 s时间内通过的路程大于一个振幅,C错误;经过周期,质点Q位于x轴下方正在接近平衡位置,D正确;经过0.5 s,波谷第一次传播到的坐标是4 m+0.5×10 m=9 m处,E正确.
【易错点】波的传播方向与质点振动方向的互判方法
2. 如图甲所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图.已知x=1 m处的质点做简谐运动的图象如图乙所示.
(1)求波传播的速度大小.
(2)从t=0时刻开始经过多长时间位于x=5 m处的质点P开始振动?并求出在0~20 s内质点P运动的路程.
甲 乙
图15?2?1
【答案】(1)0.5 m/s (2)6 s 28 cm
【解析】(1)由题图乙可知,振幅A=2 cm,质点做简谐运动的周期为T=4 s,波传播的周期也为T=4 s
由题图甲可知波长λ=2 m
波速v==0.5 m/s.
(2)由题图甲可知,x=2 m处的质点在t=0时刻刚好开始沿y轴负方向振动,设再经过Δt时间质点P开始振动,则Δt==6 s
即从t=0时刻开始经过6 s时间质点P开始振动,由简谐运动的对称性可知,质点在任意一个全振动过程中的路程s0=4A=8 cm.
质点P开始振动后14 s内经历了3.5次全振动,所以在0~20 s内质点P运动的路程为s=3.5s0=28 cm.
【易错点】波的传播方向与质点振动方向的互判方法
3. 图为一列简谐横波在t=2 s时的波形图,图(b)为媒质中平衡位置在x=1.5 m处的质点的振动图象,P是平衡位置为x=2 m的质点.下列说法正确的是( )
图(a) 图(b)
图15?3?1
A.波速为0.5 m/s
B.波的传播方向向右
C.0~2 s时间内,P运动的路程为8 cm
D.0~2 s时间内,P向y轴正方向运动
E.当t=7 s时,P恰好回到平衡位置
【答案】ACE
【解析】由题图(a)读出波长λ=2.0 m,由题图(b)读出周期T=4 s,则v==0.5 m/s,选项A正确;题图(a)是t=2 s时的波形图,题图(b)是x=1.5 m处质点的振动图象,所以该质点在t=2 s时向下振动,所以波向左传播,选项B错误;在0~2 s内质点P由波峰向波谷振动,通过的路程s=2A=8 cm,选项C正确,选项D错误;t=7 s时,P点振动了个周期,所以这时P点位置与t=T=3 s时位置相同,即在平衡位置,所以选项E正确.
【易错点】波的传播方向与质点振动方向的互判方法
4. 一列简谐横波沿x轴的正向传播,振幅为2 cm,周期为T,已知在t=0时刻波上相距40 cm的两质点a、b的位移都是1 cm,但运动方向相反,其中质点a沿y轴负向运动.如图所示,下列说法正确的是( )
图15?4?1
A.该列简谐横波波长可能为150 cm
B.该列简谐横波波长可能为12 cm
C.当质点b的位移为+2 cm时,质点a的位移为负
D.在t=时刻,质点b速度最大
E.质点a、质点b的速度始终大小相等,方向相反
【答案】BCD
【解析】根据题意,质点a、b在波的图象中的位置可能情况如图所示.有=0.4 m,可得λ=m,其中k为大于等于0的整数,波长最长为1.2 m,选项A错误;当k=3时,λ=12 cm,选项B正确;质点b再经过T时间位移为+2 cm(波峰位置),质点a再经过T到平衡位置,之后再经过T到波谷位置,选项C正确;再经过T质点b经过平衡位置,速度最大,选项D正确;两质点平衡位置间的距离等于半个波长的奇数倍时才会总是速度等大反向,而a、b两质点平衡位置间的距离不等于半个波长的奇数倍,选项E错误.
图15?4?2
【易错点】空间周期性形成的多解
5. 一半径为R的半圆柱形玻璃砖,横截面如图所示.已知玻璃的全反射临界角γ(γ<).与玻璃砖的底平面成角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上.经柱面折射后,有部分光(包括与柱面相切的入射光)能直接从玻璃砖底面射出.若忽略经半圆柱内表面反射后射出的光,求底面透光部分的宽度.
图15?5?1
【答案】
【解析】 在半圆柱形玻璃砖横截面内,考虑沿半径方向射到圆心O的光线1(如图),它在圆心处的入射角为θ1,满足θ1=γ ①
图15?5?2
恰好等于全反射临界角,发生全反射,在光线1左侧的光线(例如光线2)经过柱面折射后,射在玻璃砖底面上的入射角θ2满足θ2>γ ②
因而在底面上发生全反射,不能直接折射出.在光线1右侧的光线(例如光线3)经柱面折射后,射在玻璃砖底面上的入射角θ3满足θ3<γ ③
因而在底面上不能发生全反射,能从玻璃砖底面射出
射到半圆柱面最右侧的光线4与柱面相切,入射角i为
i= ④
由折射定律知,经圆柱面折射后的折射角
∠OAB=θ4,满足sin i=nsin θ4 ⑤
式子中,n是玻璃的折射率,由全反射角的定义知
sin γ= ⑥
联立④⑤⑥式得θ4=γ ⑦
由几何关系可得∠AOB=γ,故底面上透光部分的宽度OB=.⑧
【易错点】光的折射和全反射
【能力提升】
6. 一列简谐横波在x轴上传播,在t1=0和t2=0.05s时,其波形分别用如图所示的实线和虚线表示,求:
图15?6?1
(1)这列波可能具有的波速;
(2)当波速为280 m/s时,波的传播方向如何?以此波速传播时,x=8 m处的质点P从平衡位置运动至波谷所需的最短时间是多少?
【答案】见解析
【解析】 (1)若波沿x轴正向传播,则:Δx=Δx1+nλ=(2+8n)m,n=0,1,2,…
v==m/s=(40+160n)m/s,n=0,1,2,…
若波沿x轴负向传播,则:
Δx′=Δx2+nλ=(6+8n)m,n=0,1,2,…
v′== m/s=(120+160n)m/s,n=0,1,2,…
(2)当波速为280 m/s时,
有280=(120+160n),n=1,
所以波向x轴负方向传播,T==s
所以P质点第一次到达波谷所需最短时间为:t==s≈2.1×10-2s
【易错点】传播双向性形成的多解
7. (2018·银川模拟)下列说法正确的是( )
A.横波的两个波峰之间的距离等于一个波长
B.纵波有疏部和密部,两个相邻密部之间的距离等于一个波长
C.多普勒效应是波源与观察者之间有相对运动而发生的
D.当波源向观察者靠近时,观察者接收到的频率小于波源振动的频率
E.根据狭义相对论可知,物体的长度、时间间隔和物体的质量都是相对的
【答案】BCE
【解析】横波的两个波峰之间的距离等于若干个波长,只有相邻两个波峰之间的距离等于一个波长,选项A错误.纵波有疏部和密部,两个相邻密部之间的距离等于一个波长,选项B正确.多普勒效应是波源与观察者之间有相对运动而发生的,选项C正确.当波源向观察者靠近时,观察者接收到的频率大于波源振动的频率,选项D错误.根据狭义相对论可知,选项E正确.
【易错点】多普勒效应的成因分析
(1)接收频率:观察者接收到的频率等于观察者在单位时间内接收到的完全波的个数.
(2)当波源与观察者相互靠近时,观察者接收到的频率变大;当波源与观察者相互远离时,观察者接收到的频率变小.
8.一列横波沿x轴传播,在某一时刻x轴上相距s的两质点A、B,均处于平衡位置,且A、B间只有一个波峰,经过时间t,质点B第一次到达波峰,试求该波的传播速度.
【答案】见解析
【解析】虽然A、B间只有一个波峰,但实际上有四种波形与之相对应,如图,
图15?8?1
且波的传播方向未定,因此每种情况均有两种可能的解.
(1)图中λ=2s,波向右传播时t=,波速v1===.波向左传播时t=,波速v2===.
(2)图中λ=s,波向右传播时t=,波速v1==;波向左传播时t=,波速v2==.
(3)图中λ=s,波向右传播时t=,v1==;波向左传播时t=,波速v2==.
(4)图中λ=s,波向右传播时t=,v1==;
波向左传播时t=,波速v2==;其中8种可能的波速中有几个相同,因此有5种可能的波速为,,,,.
【易错点】解决波的多解问题的思路
一般采用从特殊到一般的思维方法,即找出一个周期内满足条件的关系Δt或Δx,若此关系为时间,则t=nT+Δt(n=0,1,2,…);若此关系为距离,则x=nλ+Δx(n=0,1,2,…).
9. 如图所示,一列水平向右传播的简谐横波,波速大小为v=0.6 m/s,P质点的平衡位置坐标为x=0.96 m.从图中状态开始计时(此时该波刚好传到距O点0.24 m的位置),求:
图15?9?1
(1)经过多长时间,P质点第一次到达波峰?
(2)经过多长时间,P质点第二次到达波谷?P质点第二次到达波谷时,P质点通过的路程及该时刻的位移为多少?
【答案】(1)1.5 s (2)1.7 s 0.25 m -5 cm
【解析】由波形图可知,波长λ=0.24 m,振幅A=5 cm,
周期T===0.4 s
(1)P质点第一次到达波峰所需的时间,就是初始时刻x=0.06 m处的质点的振动状态传到P点所需的时间,由图可知:Δx1=0.96 m-0.06 m=0.90 m
则t1== s=1.5 s
(2)为了求P质点第二次到达波谷所需的时间,可选取x=0.18 m处的质点的振动状态作为研究对象,该振动状态传到P点所需的时间再加一个周期即为所求时间,则:
Δx2=0.96 m-0.18 m=0.78 m
t2=+T= s+0.4 s=1.7 s
设波最右端传到P处所需时间为t3,有:
t3= s=1.2 s
所以从质点P起振到第二次到达波谷历时
Δt=t2-t3=1.7 s-1.2 s=0.5 s,相当于1T
所以P通过路程为
5A=0.25 m
此时刻质点P的位移为-5 cm
【易错点】波的计算
10.两束不同的单色光a、b分别斜射到半圆形玻璃砖的圆弧面上,其中a光束从圆弧面顶端入射,AB是圆的直径,且直径为d,两光束的折射光线均照射到圆直径的B端,经AB面折射后,出射光线方向相同,光线如图所示,a、b两束单色光在玻璃砖中传播的时间分别为t1、t2.
图15?10?1
(1)试证明a光束在O点的入射光线与a光束在B点的出射光线平行;
(2)试比较t1、t2的大小.
【答案】见解析
【解析】 (1)由几何关系可知,a光束在O点折射时的法线与在B点折射时的法线平行,因此a光束在O点的折射角与在B点的入射角相等,根据na=可知,a光束在O点的入射角等于在B点的折射角,故a光束在O点的入射光线与a光束在B点的出射光线平行.
图15?10?2
(2)设光在AB面上折射时的入射角为i,折射角为r,则n=
圆弧的直径为d
则光在玻璃中的传播距离为l=dsin i
光在玻璃中传播的速度为v=
因此光在玻璃中传播的时间
t==·n=·=
由此可以判断,a、b两束单色光在玻璃中传播的时间相同,即t1=t2.
【易错点】光的折射和全反射
六、课堂小结
2
20
同课章节目录
