【华师大版八年级下册进阶培优训练】第十三讲 菱形性质与判定培优辅导(含答案)
文档属性
| 名称 | 【华师大版八年级下册进阶培优训练】第十三讲 菱形性质与判定培优辅导(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-03 11:52:55 | ||
图片预览




文档简介
第十三讲 菱形性质与判定培优辅导
知识梳理
1、菱形的定义:__________________的平行四边形叫做菱形.
2、菱形的性质:菱形是特殊的平行四边形,它具有四边形和平行四边形的______:
还具有自己独特的性质
①菱形既是_____图形(两条对称轴分别是 ),也是_______对称图形;
②菱形的四条边 ______ ;
③菱形的对角线 ,并且每一条对角线平分 ;
菱形的面积S菱形=底边长×高=_________________ 。
注意:其实只要四边形的对角线互相垂直,其面积就等于____________。
3、菱形的判定:
①一组邻边相等的______ 是菱形;
②四条边______的 是菱形;
③对角线 的平行四边形是菱形.
二、经典例题《菱形的性质与应用》
【例1】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:(1)∠ABC的度数;(2)菱形ABCD的面积.
【变式题组】
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
《菱形的 判定与应用》
【例2】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
【例3】已知如图,△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于M,EF⊥BC于F.
求证:四边形AEFM是菱形.
【例4】如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,
PB+PE的最小值是,求AB的值.
三、【综合提升】
【例5】、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)①当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
②当△ABC满足什么条件时,四边形AFBD是菱形?并说明理由.
【变式题组】如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
培优升级 检测
选择题
1、若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( )
A.9cm B.8cm C.7cm D.6cm
2、过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=,∠DCF=30°,则EF的长为( )
A.2 B.3 C. D.
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A.1 B. C.2 D.+1
二、填空题
4、菱形的对角线长分别为6和8,则此菱形的周长为 ,面积为 .
5、菱形ABCD中,∠A∶∠B=1∶5,若周长为8cm,则此菱形的高等于_ _.
6、已知□ABCD,对角线AC,BD相交于点O,请你添 ,使□ABCD成为一个菱形.
7、如图所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是 .
8、如图已知菱形中,、分别是、上的点,若,求的度数 .
9、如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是 .
7题图 8题图 9题图 10题图 11题图
10、如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 .
11、如图将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值 ,菱形周长的最大值是 .
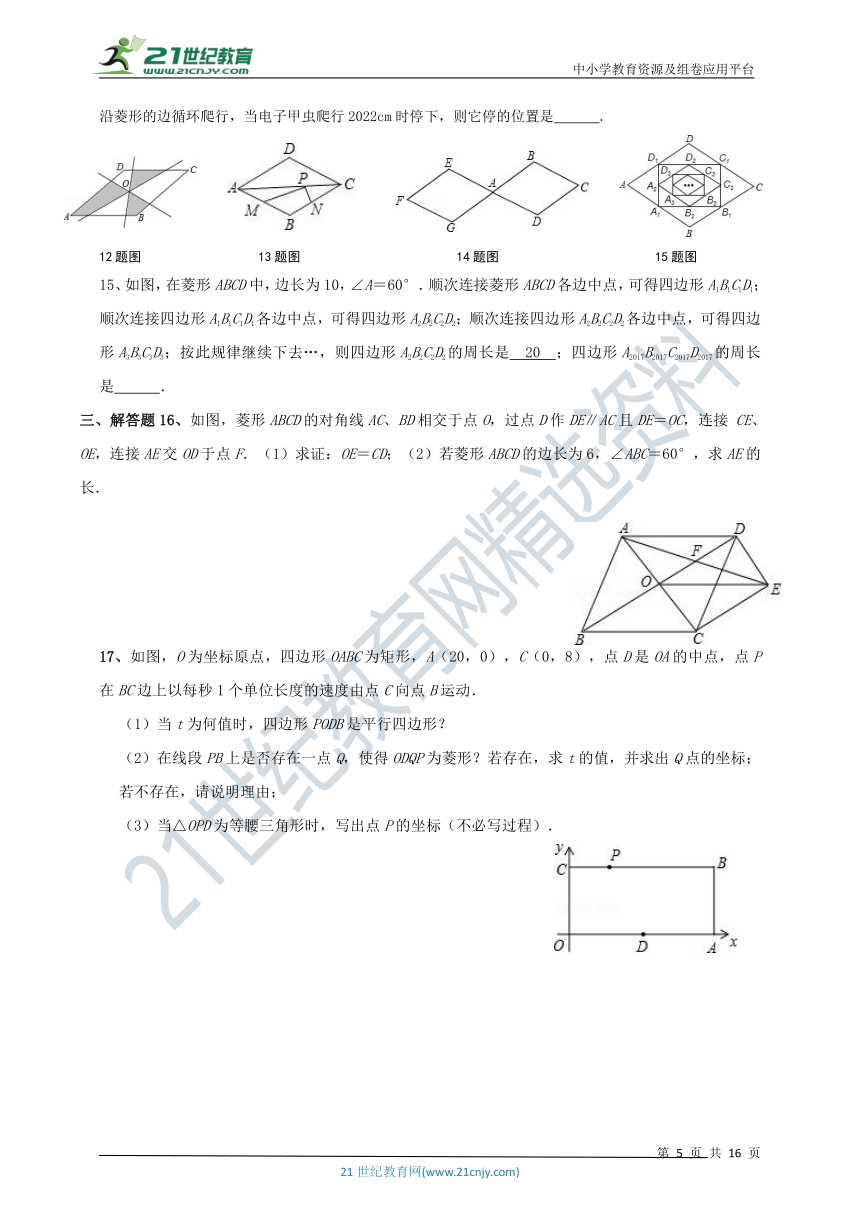
12、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
13、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 ..
14、已如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2022cm时停下,则它停的位置是 .
12题图 13题图 14题图 15题图
15、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连接四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连接四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2B2C2D2的周长是 20 ;四边形A2017B2017C2017D2017的周长是 .
三、解答题16、如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
17、如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标(不必写过程).
第十三讲 菱形性质与判定培优辅导答案
知识梳理
1、菱形的定义:__有一组邻边相等_的平行四边形叫做菱形.
2、菱形的性质:菱形是特殊的平行四边形,它不仅具有四边形和平行四边形的_一切性质____,还具有自己独特的性质。
①菱形既是_轴对称_图形(两条对称轴分别是 对角线所在的直线 ),也是中心___对称图形;
②菱形的四条边 _相等___;
③菱形的对角线 互相垂直平分 ,并且每一条对角线平分 每一组对角 ;
菱形的面积S菱形=底边长×高=__对角线之积的一半_ 。
注意:其实只要四边形的对角线互相垂直,其面积就等于_对角线之积的一半_。
3、菱形的判定:
①一组邻边相等的_平行四边形__ 是菱形;
②四条边_相等_的 四边形 是菱形;
③对角线 互相垂直 的平行四边形是菱形.
二、经典例题《菱形的性质与应用》
【例1】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:(1)∠ABC的度数;(2)菱形ABCD的面积.
解:(1)连接BD交AC于点O, 在菱形ABCD中
AD=AB
∵E是AB的中点,且DE⊥AB ∴AD=BD, ∴AD=BD=AB
∴△ABD为等边三角形, ∴∠BAD=60°, ∴∠ABC=120°. (2)在Rt△ABO中,∠BAO=30°,AB=4, 则BO=2故A0=2
∴菱形ABCD的面积
【变式题组】
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
解:(1)证明:∵菱形ABCD的边长为2,BD=2,
∴△ABD和△BCD都为正三角形, ∴∠BDE=∠BCF=60°,BD=BC, ∵AE+DE=AD=2,而AE+CF=2, ∴DE=CF, ∴△BDE≌△BCF; (2)解:△BEF为正三角形.理由: ∵△BDE≌△BCF, ∴∠DBE=∠CBF,BE=BF, ∵∠DBC=∠DBF+∠CBF=60°, ∴∠DBF+∠DBE=60°即∠EBF=60°, ∴△BEF为正三角形; (3)解:设BE=BF=EF=x, 当BE⊥AD时,x最小=, ∴S最小=×=, 当BE与AB重合时,x最大=2, ∴S最大=×2×2=, ∴.
《菱形的 判定与应用》
【例2】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
(1)证明:∵AB∥CD,即AE∥CD, 又∵CE∥AD, ∴四边形AECD是平行四边形. ∵AC平分∠BAD,∴∠CAE=∠CAD, ∵AD∥CE,∴∠ACE=∠CAD, ∴∠ACE=∠CAE,∴AE=CE, ∴四边形AECD是菱形; (2)解:△ABC是直角三角形. 证法一:∵E是AB中点,∴AE=BE. 又∵AE=CE,∴BE=CE,∴∠B=∠BCE, ∵∠B+∠BCA+∠BAC=180°, ∴2∠BCE+2∠ACE=180°, ∴∠BCE+∠ACE=90°.即∠ACB=90°, ∴△ABC是直角三角形. 证法二:连DE,由四边形AECD是菱形,得到DE⊥AC,且平分AC, 设DE交AC于F,∵E是AB的中点,且F为AC中点, ∴EF∥BC.∠AFE=90°, ∴∠ACB=∠AFE=90°,∴BC⊥AC, ∴△ABC是直角三角形.
【变式题组】如图,在四边形ABCD中,ADBC,AM⊥BC,垂足为M,AN⊥DC,垂足为N. 若∠BAD=∠BCD,AM=AN,求证四边形ABCD是菱形.
证明:∵AD∥BC, ∴∠B+∠BAD=180°,∠D+∠C=180°, ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴∠AMB=∠AND=90°, 在△ABM和△ADN中,∠B=∠D,∠AMB=∠AND=90°,AM=AN,
∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.(也可用等积法证邻边等)
【例3】已知如图,△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于M,EF⊥BC于F.
求证:四边形AEFM是菱形.
证明:∵AD⊥BC,EF⊥BC ∴AD∥EF,∴∠AME=∠MEF, ∵BE平分∠ABC,∠BAC=90°,EF⊥BC, ∴EA=EF,∠AFB=∠FEM
∵AN平分∠DAC, ∴∠CAN=∠DAN,
∴∠AME=∠AEM, ∴AM=AE
∴AM=EF ∴四边形AMFE是平行四边形,且AM=AE
∴平行四边形AMNE是菱形.
【例4】如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,
PB+PE的最小值是,求AB的值.
解:由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB, ∴PE+PB=PE+PD=DE, 即DE就是PE+PB的最小值, ∵∠BAD=60°,AD=AB, ∴△ABD是等边三角形, ∵AE=BE, ∴DE⊥AB(等腰三角形三线合一的性质) 在Rt△ADE中,DE=,∠BAD=60°
∴AD=2.
三、【综合提升】
【例5】、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)①当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
②当△ABC满足什么条件时,四边形AFBD是菱形?并说明理由.
【解答】(1)证明:∵E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠ECD,
在△AEF和△DEC中,
,
∴△AEF≌△DEC,
∴AF=DC,
∵AF=BD,
∴BD=DC.
(2)①当AB=AC时,四边形AFBD是矩形.
证明:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AFBD是矩形.
②当∠BAC=90°时,四边形AFBD是菱形.
证明:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,BD=DC,
∴AD=BD=DC,
∴四边形AFBD是菱形.
【变式题组】如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
解:(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t, ∴DF=t,又∵AE=t,∴AE=DF; (2)能;理由如下: ∵AB⊥BC,DF⊥BC, ∴AE∥DF,又AE=DF, ∴四边形AEFD为平行四边形, ∵AB=5,∴AC=2,AB=10, ∴AD=AC-DC=10-2t, 若使为菱形,则需AE=AD,即t=10-2t,t=, 即当t=时,四边形AEFD为菱形; (3)①∠EDF=90°时,四边形EBFD为矩形, 在Rt△AED中,∠ADE=∠C=30°, ∴AD=2AE,即10-2t=2t,t=; ②∠DEF=90°时,由(2)知EF∥AD, ∴∠ADE=∠DEF=90°, ∵∠A=90°-∠C=60°, ∴AD=AE,即10-2t=t,t=4; ③∠EFD=90°时,此种情况不存在; 综上所述,当或4时,△DEF为直角三角形。
培优升级 检测
选择题
1、若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( D )
A.9cm B.8cm C.7cm D.6cm
2、过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=,∠DCF=30°,则EF的长为( A )
A.2 B.3 C. D.
3、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( B )
A.1 B. C.2 D.+1
二、填空题
4、菱形的对角线长分别为6和8,则此菱形的周长为 20 ,面积为 24 .
5、菱形ABCD中,∠A∶∠B=1∶5,若周长为8cm,则此菱形的高等于___1__.
6、已知□ABCD,对角线AC,BD相交于点O,请你添 答案不唯一如AB=BC,使□ABCD成为一个菱形.
7、如图所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是______.
8、如图已知菱形中,、分别是、上的点,若,求的度数100° .
9、如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是___3个___.
7题图 8题图 9题图 10题图 11题图
10、如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 4.8 .
11、如图将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值___12_____,菱形周长的最大值是_________.
12、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 12 .
13、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 5 ..
14、已如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2022cm时停下,则它停的位置是__点F____.
12题图 13题图 14题图 15题图
15、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连接四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连接四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2B2C2D2的周长是 20 ;四边形A2017B2017C2017D2017的周长是 .
【解答】解:∵菱形ABCD中,边长为10,∠A=60°,顺次连结菱形ABCD各边中点,
∴△AA1D1是等边三角形,四边形A2B2C2D2是菱形,
∴A1D1=5,C1D1=AC=5,A2B2=C2D2=C2B2=A2D2=5,
∴四边形A2B2C2D2的周长是:5×4=20,
同理可得出:A3D3=5×,C3D3=C1D1=×5,
A5D5=5×()2,C5D5=C3D3=()2×5,
…
∴四边形A2015B2015C2015D2015的周长是:,故答案为:20;.
三、解答题
16、如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
【解答】(1)证明:∵四边形ABCD是菱形,DE=AC,
∴AC⊥BD,DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,四边形OCED是平行四边形,
∴四边形OCED是矩形,
∴OE=CD.
(2)解:∵菱形ABCD的边长为6,
∴AB=BC=CD=AD=6,BD⊥AC,AO=CO=AC.
∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=6,
∵△AOD中BD⊥AC,AD=6,AO=3,
∴OD==3,
∵四边形OCED是矩形,
∴CE=OD=3,
∵在Rt△ACE中,AC=6,CE=3,
∴AE===3.
17、如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标(不必写过程).
【解答】解:(1)∵A(20,0),C(0,8),
∴OA=20,OC=8,
∵点D是OA的中点,
∴OD=OA=10,
∵四边形OABC为矩形,
∴BC=OA=20,
∵四边形PODB是平行四边形,
∴PB=OD=10,
∴PC=BC﹣PB=10,
∴t=10;
(2)如图1,∵四边形ODQP为菱形,
∴OD=OP=PQ=10,
∴在Rt△OPC中,由勾股定理得:PC==6,
∴t=6,
∴CQ=CP+PQ=6+10=16,
∴Q点的坐标为(16,8);
(3)如图2,△OPD为等腰三角形时,分三种情况:
①如果O为顶点,那么OP=OD=10,
由勾股定理可以求得PC=6,此时P1(6,8);
②如果P为顶点,那么PO=PD,
作PE⊥OA于E,则OE=ED=5,此时P2(5,8);
③如果D为顶点,那么DP=DO=10,
作DF⊥BC于F,由勾股定理,得PF=6,
∴P3C=10﹣6=4或P4C=10+6=16,此时P3(4,8),P4(16,8).
综上所述,满足条件的点P的坐标为P1(6,8),P2(5,8),P3(4,8),P4(16,8).
知识梳理
1、菱形的定义:__________________的平行四边形叫做菱形.
2、菱形的性质:菱形是特殊的平行四边形,它具有四边形和平行四边形的______:
还具有自己独特的性质
①菱形既是_____图形(两条对称轴分别是 ),也是_______对称图形;
②菱形的四条边 ______ ;
③菱形的对角线 ,并且每一条对角线平分 ;
菱形的面积S菱形=底边长×高=_________________ 。
注意:其实只要四边形的对角线互相垂直,其面积就等于____________。
3、菱形的判定:
①一组邻边相等的______ 是菱形;
②四条边______的 是菱形;
③对角线 的平行四边形是菱形.
二、经典例题《菱形的性质与应用》
【例1】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:(1)∠ABC的度数;(2)菱形ABCD的面积.
【变式题组】
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
《菱形的 判定与应用》
【例2】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
【例3】已知如图,△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于M,EF⊥BC于F.
求证:四边形AEFM是菱形.
【例4】如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,
PB+PE的最小值是,求AB的值.
三、【综合提升】
【例5】、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)①当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
②当△ABC满足什么条件时,四边形AFBD是菱形?并说明理由.
【变式题组】如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
培优升级 检测
选择题
1、若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( )
A.9cm B.8cm C.7cm D.6cm
2、过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=,∠DCF=30°,则EF的长为( )
A.2 B.3 C. D.
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A.1 B. C.2 D.+1
二、填空题
4、菱形的对角线长分别为6和8,则此菱形的周长为 ,面积为 .
5、菱形ABCD中,∠A∶∠B=1∶5,若周长为8cm,则此菱形的高等于_ _.
6、已知□ABCD,对角线AC,BD相交于点O,请你添 ,使□ABCD成为一个菱形.
7、如图所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是 .
8、如图已知菱形中,、分别是、上的点,若,求的度数 .
9、如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是 .
7题图 8题图 9题图 10题图 11题图
10、如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 .
11、如图将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值 ,菱形周长的最大值是 .
12、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
13、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 ..
14、已如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2022cm时停下,则它停的位置是 .
12题图 13题图 14题图 15题图
15、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连接四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连接四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2B2C2D2的周长是 20 ;四边形A2017B2017C2017D2017的周长是 .
三、解答题16、如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
17、如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标(不必写过程).
第十三讲 菱形性质与判定培优辅导答案
知识梳理
1、菱形的定义:__有一组邻边相等_的平行四边形叫做菱形.
2、菱形的性质:菱形是特殊的平行四边形,它不仅具有四边形和平行四边形的_一切性质____,还具有自己独特的性质。
①菱形既是_轴对称_图形(两条对称轴分别是 对角线所在的直线 ),也是中心___对称图形;
②菱形的四条边 _相等___;
③菱形的对角线 互相垂直平分 ,并且每一条对角线平分 每一组对角 ;
菱形的面积S菱形=底边长×高=__对角线之积的一半_ 。
注意:其实只要四边形的对角线互相垂直,其面积就等于_对角线之积的一半_。
3、菱形的判定:
①一组邻边相等的_平行四边形__ 是菱形;
②四条边_相等_的 四边形 是菱形;
③对角线 互相垂直 的平行四边形是菱形.
二、经典例题《菱形的性质与应用》
【例1】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:(1)∠ABC的度数;(2)菱形ABCD的面积.
解:(1)连接BD交AC于点O, 在菱形ABCD中
AD=AB
∵E是AB的中点,且DE⊥AB ∴AD=BD, ∴AD=BD=AB
∴△ABD为等边三角形, ∴∠BAD=60°, ∴∠ABC=120°. (2)在Rt△ABO中,∠BAO=30°,AB=4, 则BO=2故A0=2
∴菱形ABCD的面积
【变式题组】
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
解:(1)证明:∵菱形ABCD的边长为2,BD=2,
∴△ABD和△BCD都为正三角形, ∴∠BDE=∠BCF=60°,BD=BC, ∵AE+DE=AD=2,而AE+CF=2, ∴DE=CF, ∴△BDE≌△BCF; (2)解:△BEF为正三角形.理由: ∵△BDE≌△BCF, ∴∠DBE=∠CBF,BE=BF, ∵∠DBC=∠DBF+∠CBF=60°, ∴∠DBF+∠DBE=60°即∠EBF=60°, ∴△BEF为正三角形; (3)解:设BE=BF=EF=x, 当BE⊥AD时,x最小=, ∴S最小=×=, 当BE与AB重合时,x最大=2, ∴S最大=×2×2=, ∴.
《菱形的 判定与应用》
【例2】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
(1)证明:∵AB∥CD,即AE∥CD, 又∵CE∥AD, ∴四边形AECD是平行四边形. ∵AC平分∠BAD,∴∠CAE=∠CAD, ∵AD∥CE,∴∠ACE=∠CAD, ∴∠ACE=∠CAE,∴AE=CE, ∴四边形AECD是菱形; (2)解:△ABC是直角三角形. 证法一:∵E是AB中点,∴AE=BE. 又∵AE=CE,∴BE=CE,∴∠B=∠BCE, ∵∠B+∠BCA+∠BAC=180°, ∴2∠BCE+2∠ACE=180°, ∴∠BCE+∠ACE=90°.即∠ACB=90°, ∴△ABC是直角三角形. 证法二:连DE,由四边形AECD是菱形,得到DE⊥AC,且平分AC, 设DE交AC于F,∵E是AB的中点,且F为AC中点, ∴EF∥BC.∠AFE=90°, ∴∠ACB=∠AFE=90°,∴BC⊥AC, ∴△ABC是直角三角形.
【变式题组】如图,在四边形ABCD中,ADBC,AM⊥BC,垂足为M,AN⊥DC,垂足为N. 若∠BAD=∠BCD,AM=AN,求证四边形ABCD是菱形.
证明:∵AD∥BC, ∴∠B+∠BAD=180°,∠D+∠C=180°, ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴∠AMB=∠AND=90°, 在△ABM和△ADN中,∠B=∠D,∠AMB=∠AND=90°,AM=AN,
∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.(也可用等积法证邻边等)
【例3】已知如图,△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于M,EF⊥BC于F.
求证:四边形AEFM是菱形.
证明:∵AD⊥BC,EF⊥BC ∴AD∥EF,∴∠AME=∠MEF, ∵BE平分∠ABC,∠BAC=90°,EF⊥BC, ∴EA=EF,∠AFB=∠FEM
∵AN平分∠DAC, ∴∠CAN=∠DAN,
∴∠AME=∠AEM, ∴AM=AE
∴AM=EF ∴四边形AMFE是平行四边形,且AM=AE
∴平行四边形AMNE是菱形.
【例4】如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,
PB+PE的最小值是,求AB的值.
解:由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB, ∴PE+PB=PE+PD=DE, 即DE就是PE+PB的最小值, ∵∠BAD=60°,AD=AB, ∴△ABD是等边三角形, ∵AE=BE, ∴DE⊥AB(等腰三角形三线合一的性质) 在Rt△ADE中,DE=,∠BAD=60°
∴AD=2.
三、【综合提升】
【例5】、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)①当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
②当△ABC满足什么条件时,四边形AFBD是菱形?并说明理由.
【解答】(1)证明:∵E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠ECD,
在△AEF和△DEC中,
,
∴△AEF≌△DEC,
∴AF=DC,
∵AF=BD,
∴BD=DC.
(2)①当AB=AC时,四边形AFBD是矩形.
证明:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AFBD是矩形.
②当∠BAC=90°时,四边形AFBD是菱形.
证明:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,BD=DC,
∴AD=BD=DC,
∴四边形AFBD是菱形.
【变式题组】如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
解:(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t, ∴DF=t,又∵AE=t,∴AE=DF; (2)能;理由如下: ∵AB⊥BC,DF⊥BC, ∴AE∥DF,又AE=DF, ∴四边形AEFD为平行四边形, ∵AB=5,∴AC=2,AB=10, ∴AD=AC-DC=10-2t, 若使为菱形,则需AE=AD,即t=10-2t,t=, 即当t=时,四边形AEFD为菱形; (3)①∠EDF=90°时,四边形EBFD为矩形, 在Rt△AED中,∠ADE=∠C=30°, ∴AD=2AE,即10-2t=2t,t=; ②∠DEF=90°时,由(2)知EF∥AD, ∴∠ADE=∠DEF=90°, ∵∠A=90°-∠C=60°, ∴AD=AE,即10-2t=t,t=4; ③∠EFD=90°时,此种情况不存在; 综上所述,当或4时,△DEF为直角三角形。
培优升级 检测
选择题
1、若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( D )
A.9cm B.8cm C.7cm D.6cm
2、过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=,∠DCF=30°,则EF的长为( A )
A.2 B.3 C. D.
3、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( B )
A.1 B. C.2 D.+1
二、填空题
4、菱形的对角线长分别为6和8,则此菱形的周长为 20 ,面积为 24 .
5、菱形ABCD中,∠A∶∠B=1∶5,若周长为8cm,则此菱形的高等于___1__.
6、已知□ABCD,对角线AC,BD相交于点O,请你添 答案不唯一如AB=BC,使□ABCD成为一个菱形.
7、如图所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是______.
8、如图已知菱形中,、分别是、上的点,若,求的度数100° .
9、如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是___3个___.
7题图 8题图 9题图 10题图 11题图
10、如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 4.8 .
11、如图将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值___12_____,菱形周长的最大值是_________.
12、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 12 .
13、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 5 ..
14、已如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2022cm时停下,则它停的位置是__点F____.
12题图 13题图 14题图 15题图
15、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连接四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连接四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2B2C2D2的周长是 20 ;四边形A2017B2017C2017D2017的周长是 .
【解答】解:∵菱形ABCD中,边长为10,∠A=60°,顺次连结菱形ABCD各边中点,
∴△AA1D1是等边三角形,四边形A2B2C2D2是菱形,
∴A1D1=5,C1D1=AC=5,A2B2=C2D2=C2B2=A2D2=5,
∴四边形A2B2C2D2的周长是:5×4=20,
同理可得出:A3D3=5×,C3D3=C1D1=×5,
A5D5=5×()2,C5D5=C3D3=()2×5,
…
∴四边形A2015B2015C2015D2015的周长是:,故答案为:20;.
三、解答题
16、如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
【解答】(1)证明:∵四边形ABCD是菱形,DE=AC,
∴AC⊥BD,DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,四边形OCED是平行四边形,
∴四边形OCED是矩形,
∴OE=CD.
(2)解:∵菱形ABCD的边长为6,
∴AB=BC=CD=AD=6,BD⊥AC,AO=CO=AC.
∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=6,
∵△AOD中BD⊥AC,AD=6,AO=3,
∴OD==3,
∵四边形OCED是矩形,
∴CE=OD=3,
∵在Rt△ACE中,AC=6,CE=3,
∴AE===3.
17、如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标(不必写过程).
【解答】解:(1)∵A(20,0),C(0,8),
∴OA=20,OC=8,
∵点D是OA的中点,
∴OD=OA=10,
∵四边形OABC为矩形,
∴BC=OA=20,
∵四边形PODB是平行四边形,
∴PB=OD=10,
∴PC=BC﹣PB=10,
∴t=10;
(2)如图1,∵四边形ODQP为菱形,
∴OD=OP=PQ=10,
∴在Rt△OPC中,由勾股定理得:PC==6,
∴t=6,
∴CQ=CP+PQ=6+10=16,
∴Q点的坐标为(16,8);
(3)如图2,△OPD为等腰三角形时,分三种情况:
①如果O为顶点,那么OP=OD=10,
由勾股定理可以求得PC=6,此时P1(6,8);
②如果P为顶点,那么PO=PD,
作PE⊥OA于E,则OE=ED=5,此时P2(5,8);
③如果D为顶点,那么DP=DO=10,
作DF⊥BC于F,由勾股定理,得PF=6,
∴P3C=10﹣6=4或P4C=10+6=16,此时P3(4,8),P4(16,8).
综上所述,满足条件的点P的坐标为P1(6,8),P2(5,8),P3(4,8),P4(16,8).
