五年级上册数学一课一练-5.多边形面积的计算 西师大版(2014秋)(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-5.多边形面积的计算 西师大版(2014秋)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-04 22:48:04 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-5.多边形面积的计算
一、单选题
1.平行四边形的面积是(?? )
A.?30平方米????????????????????????B.?36平方厘米????????????????????????C.?12平方厘米????????????????????????D.?21平方米
2.一个三角形和一个平行四边形的面积相等,底边的长也相等,已知平行四边形的高是6厘米,三角形的高是(? )厘米.
A.?3???????????????????????????????????????B.?6???????????????????????????????????????C.?12???????????????????????????????????????D.?无法确定
3.一个平行四边形的两条边分别为12厘米和8厘米,其中一条边上的高是10厘米,这个平行四边形的面积是(? )平方厘米.
A.?96?????????????????????????????????????B.?120?????????????????????????????????????C.?80?????????????????????????????????????D.?80或120
4.一个梯形的上底增加3厘米,下底减少3厘米,要使梯形的面积不变,高(??? )。
A.?变小了???????????????????????????????????????B.?不变???????????????????????????????????????C.?变大了
5.两个同底等高的三角形,它们的( )一定相等。
A.?形状?????????????????????????????????????????B.?面积?????????????????????????????????????????C.?周长
二、判断题
6.面积相同的两个梯形,形状完全相同。
7.右图中的阴影部分面积占长方形的 。
8.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.
9.如果一个平行四边形和一个长方形的周长相等,那么面积也一定相等。
三、填空题
10.有一个三角形,底长1.25米,高是0.8米,这个三角形的面积是________平方米
11.平行四边形的面积:________cm2
12.下图平行四边形的面积是15cm2 , 阴影部分的面积是________.
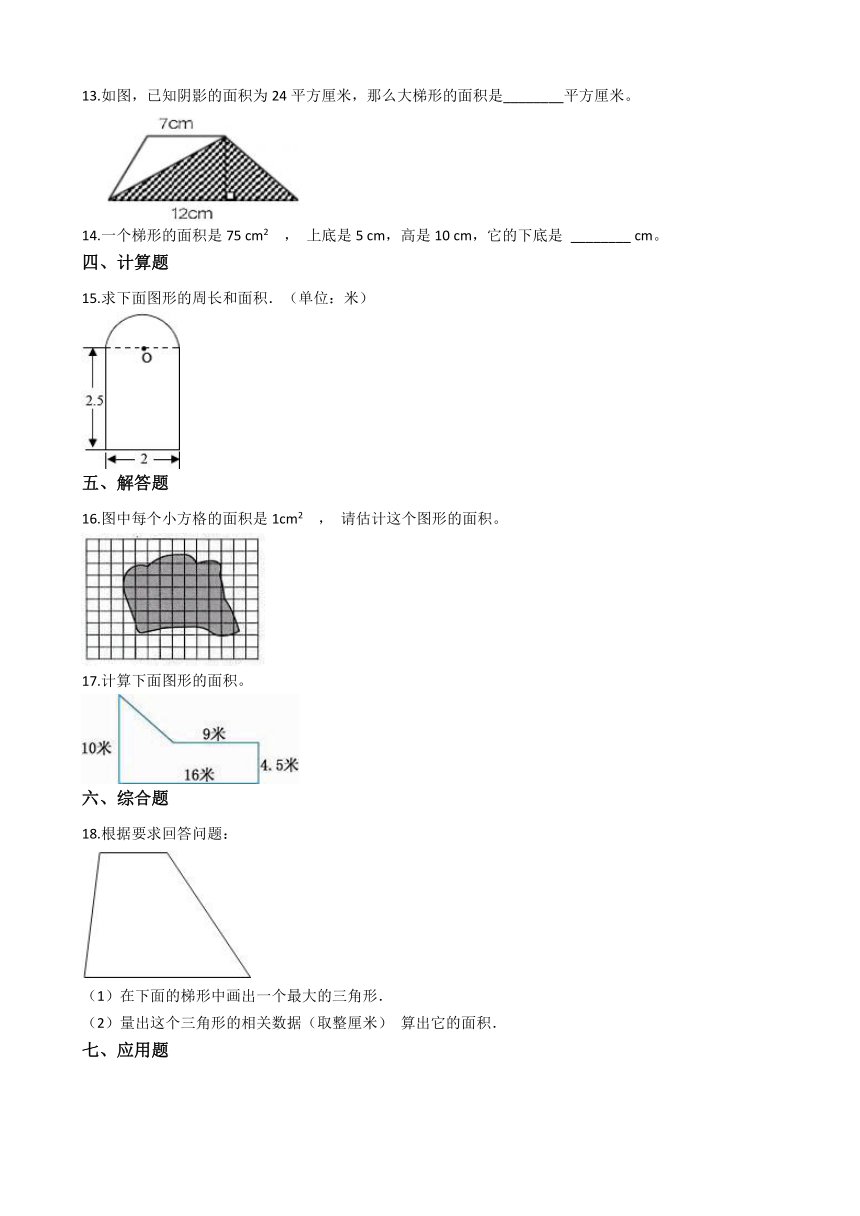
13.如图,已知阴影的面积为24平方厘米,那么大梯形的面积是________平方厘米。
14.一个梯形的面积是75 cm2 , 上底是5 cm,高是10 cm,它的下底是 ________?cm。
四、计算题
15.求下面图形的周长和面积.(单位:米)
五、解答题
16.图中每个小方格的面积是1cm2 , 请估计这个图形的面积。
17.计算下面图形的面积。
六、综合题
18.根据要求回答问题:
(1)在下面的梯形中画出一个最大的三角形.
(2)量出这个三角形的相关数据(取整厘米) 算出它的面积.
七、应用题
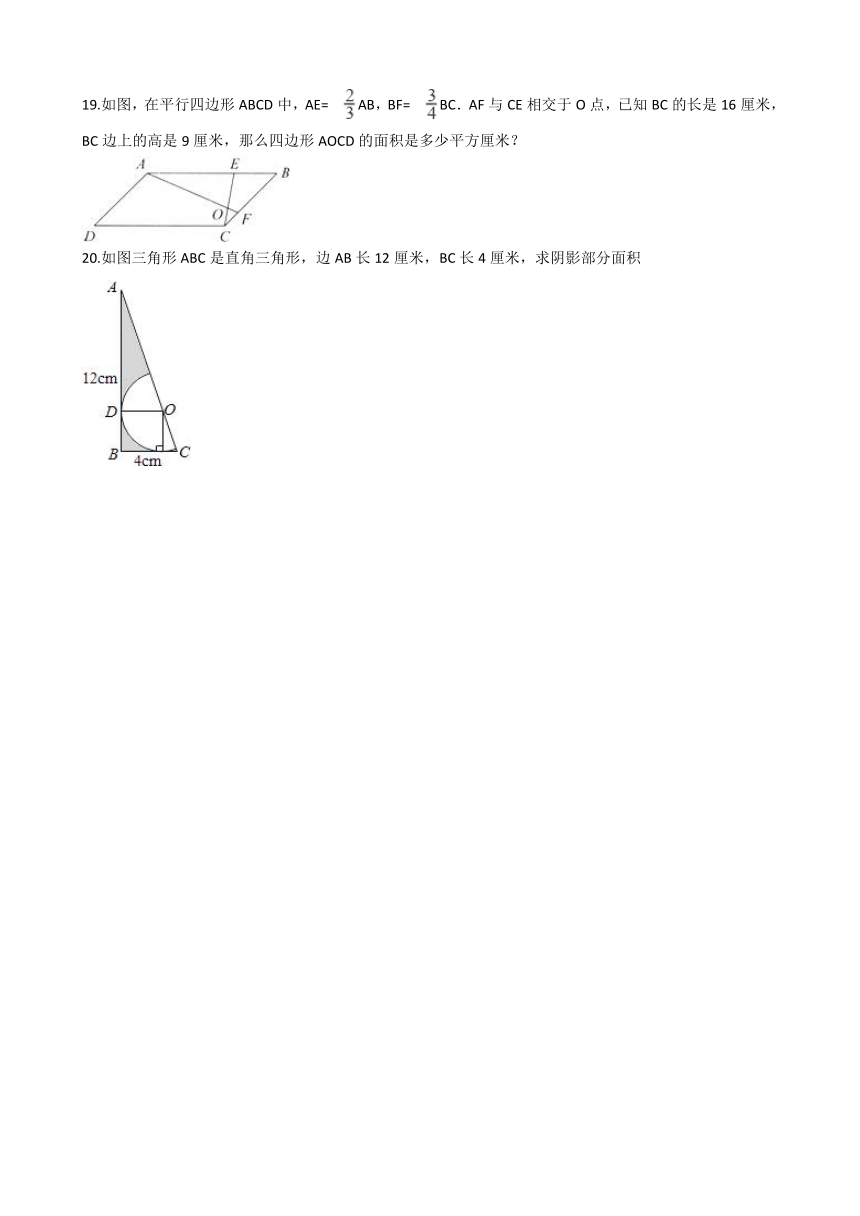
19.如图,在平行四边形ABCD中,AE= AB,BF= BC.AF与CE相交于O点,已知BC的长是16厘米,BC边上的高是9厘米,那么四边形AOCD的面积是多少平方厘米?
20.如图三角形ABC是直角三角形,边AB长12厘米,BC长4厘米,求阴影部分面积
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】3.5×6=21(平方米)
故答案为:D
【分析】底是3.5m,高是6m,根据“平行四边形面积=底×高”列式计算面积.
2.【答案】 C
【解析】【解答】解:6÷ =12(厘米).
答:三角形的高是12厘米.
故选:C.
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,由“一个三角形和一个平行四边形的底相等,面积也相等”可知,平行四边形的高是三角形的高的 ,从而问题得解.
3.【答案】C
【解析】【解答】解:10×8=80(平方厘米);
答:这个平行四边形的面积是80平方厘米.
故选:C.
【分析】依据在直角三角形中斜边最长,先判断出10厘米高的对应底边是8厘米,进而利用平行四边形的面积公式即可求解.解答此题的关键是:先确定出已知高的对应底边,即可求其面积.
4.【答案】B
【解析】【解答】因为梯形的面积=(上底+下底)×高÷2,“上底增加3厘米,下底减少3厘米,面积不变”则(上底+下底)的和不变,且面积不变,所以梯形的高不变。
故选:B
【分析】梯形的面积=(上底+下底)×高÷2,若“上底增加3米,下底减少3米,面积不变”则(上底+下底)的和不变,且面积不变,从而得知梯形的高也不变。
5.【答案】 B
【解析】【解答】三角形的面积为:面积=底×高÷2
则:同底等高的两个三角形的面积一定相等。
【分析】根据三角形的面积公式=底×高÷2,可知三角形面积的大小是由它的底和高决定的,所以同底等高的两个三角形的面积一定相等。掌握同底等高的两个三角形的面积相等。
二、判断题
6.【答案】错误
【解析】【解答】面积相同的两个梯形,形状可能相同,可能不同,原题说法错误.
故答案为:错误.
【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此判断.
7.【答案】正确
【解析】【解答】解:(2×2÷2×2)÷(2×8)
=4÷16
=
原题计算正确.
故答案为:正确
【分析】两块阴影部分是等底等高的三角形,根据面积公式分别计算阴影部分的面积之和和长方形的面积,用阴影部分面积除以长方形面积即可.
8.【答案】正确
【解析】【解答】解:拿走一个小方块,大正方体的表面看似少了三个面,其实又多出来三个面,所以它的表面积是不变的.
故答案为:正确.
【分析】由题意知,拼成的正方体长、宽、高应该都是2厘米,即上下各4个小方块,且每个小方块都处在一个角上,每个小方块都有三个面组成大正方体的表面,拿走一个,就少三个面,但又多了三个面,从而题目得解.此题主要考查正方体的表面积,关键是弄清楚少了三个面,又多了三个面.
9.【答案】错误
【解析】【解答】解:如果一个平行四边形和一个长方形的周长相等,但面积不一定相等。
故答案为:错误。
【分析】平行四边形的周长=(底+腰)×2,长方形的周长=(长+宽)×2,如果一个平行四边形和一个长方形的周长相等,即平行四边形的底+腰=长方形的长+宽,它们之间只存在一个等量关系,并不要求对应相等,而平行四边形的面积=底×高,长方形的面积=长×宽,所以它们的面积不一定相等。
三、填空题
10.【答案】0.5
【解析】【解答】解:1.25×0.8÷2=0.5(平方米)
故答案为:0.5平方米
【分析】本题考查的主要内容是三角形的面积计算问题,根据三角形的面积=底×高÷2进行分析即可.
11.【答案】72
【解析】【解答】解:8×9=72(平方厘米)
故答案为:72.
【分析】本题考查的主要内容是平行四边形的面积的应用问题,根据平行四边形的面积公式进行分析即可.
12.【答案】7.5平方厘米
【解析】【解答】解:15÷2=7.5(平方厘米)则阴影部分的面积是7.5平方厘米.
故答案为:7.5平方厘米.
【分析】阴影部分的三角形与平行四边形等底等高,所以三角形面积是平行四边形面积的一半,由此用平行四边形面积除以2就是阴影部分的面积.
13.【答案】38
【解析】【解答】解:24×2÷12=4(厘米),梯形面积:
(7+12)×4÷2
=19×4÷2
=38(平方厘米)。
故答案为:38。
【分析】用阴影部分三角形面积的2倍除以底即可求出高,梯形的高与三角形的高相等,再根据梯形面积公式计算大梯形面积即可。
14.【答案】10
【解析】【解答】75×2÷10-5
=150÷10-5
=15-5
=10(cm)
故答案为:10.【分析】已知梯形的面积及上底和高,求梯形的下底,用梯形的面积×2÷高-上底=下底,据此列式解答.
四、计算题
15.【答案】解:周长:2.5×2+2+3.14×2÷2,
=5+2+3.14,
=10.14(米),
面积:2.5×2+3.14× ÷2,
=5+3.14×1÷2,
=5+1.57,
=6.57(平方米),
答:这个图形的周长是10.14米,面积是6.57平方米
【解析】【分析】(1)要求它的周长,可用长方形的2个长+一个宽+圆的周长的一半;(2)要求它的面积,可用图中长方形的面积加上半圆的面积即可.组合图形的计算,一般都要把它转移到规则图形中进行计算.
五、解答题
16.【答案】解:6×8=48(cm2)(答案不唯一)
答:估计这个图形的面积是48平方厘米。
【解析】【分析】可以把它看作一个近似的平行四边形来计算面积,底是8cm,高是6cm,用底乘高求出面积即可。
17.【答案】解:(16-9)×(10-4.5)÷2+16×4.5
=7×5.5÷2+72
=19.25+72
=91.25(平方米)
答:图形的面积是91.25平方米.
【解析】【分析】根据题意可知,组合图形可以分成一个三角形和一个长方形,三角形的底是10-4.5=5.5米,三角形的高是16-9=7米,然后用三角形的面积+长方形的面积=组合图形的面积,据此列式解答.
六、综合题
18.【答案】 (1)如图所示:
(2)解:测量可得:三角形底4厘米,高3厘米,
4×3÷2=6(平方厘米)
答:它的面积是6平方厘米.
【解析】【分析】(1)梯形中面积最大的三角形是以梯形较长底边为底,与梯形等高的三角形;(2)先量出三角形的底和高,再根据三角形的面积公式:三角形面积=底×高÷2计算即可.解答此题的关键是明确梯形中面积最大的三角形是指哪一部分.
七、应用题
19.【答案】解:因为BF= BC=3FC,所以S△ABF=3S△AFC,S△BOF=3△FOC,故S△ABO=3S△AOC;
又AE= AB=2BE,所以SABO= △S△AOE,S△AEC= S△ABC,
故S△AOC= S△AOE= S△AEC= S△ABC.
而S△ABC=S△ACD= SABCD= ×16×9=72(平方厘米),
因此四边形AOCD的面积=S△AOC+S△ACD= ×72+72=16+72=88(平方厘米).
答:四边形AOCD的面积是88平方厘米.
【解析】【分析】要求四边形AOCD的面积,只要求出三角形AOC和ACD的面积即可,可以通过作辅助线加以解答.如图,连接AC和OB.此题设计较精彩,融合了三角形、四边形与多边形的面积与一体,重在考查学生对平面图形面积计算的分析与掌握情况.
20.【答案】解:设半圆的半径为x厘米,则
(12﹣x):12=x:4
????????? 12x=4(12﹣x)
????????? 12x=48﹣4x
????????? 16x=48
??? 16x÷16=48÷16
???????????? x=3
12×4÷2﹣3.14×32÷2
=24﹣3.14×9÷2
=24﹣14.13
=9.87(平方厘米)
答:阴影部分面积是9.87平方厘米
【解析】【分析】首先根据相似三角形的性质得到半圆的半径,再根据阴影部分面积=三角形的面积﹣半圆的面积,代入数据计算即可求解.考查了组合图形的面积,本题关键是理解阴影部分面积=三角形的面积﹣半圆的面积,难点是得到半圆的半径.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-5.多边形面积的计算
一、单选题
1.平行四边形的面积是(?? )
A.?30平方米????????????????????????B.?36平方厘米????????????????????????C.?12平方厘米????????????????????????D.?21平方米
2.一个三角形和一个平行四边形的面积相等,底边的长也相等,已知平行四边形的高是6厘米,三角形的高是(? )厘米.
A.?3???????????????????????????????????????B.?6???????????????????????????????????????C.?12???????????????????????????????????????D.?无法确定
3.一个平行四边形的两条边分别为12厘米和8厘米,其中一条边上的高是10厘米,这个平行四边形的面积是(? )平方厘米.
A.?96?????????????????????????????????????B.?120?????????????????????????????????????C.?80?????????????????????????????????????D.?80或120
4.一个梯形的上底增加3厘米,下底减少3厘米,要使梯形的面积不变,高(??? )。
A.?变小了???????????????????????????????????????B.?不变???????????????????????????????????????C.?变大了
5.两个同底等高的三角形,它们的( )一定相等。
A.?形状?????????????????????????????????????????B.?面积?????????????????????????????????????????C.?周长
二、判断题
6.面积相同的两个梯形,形状完全相同。
7.右图中的阴影部分面积占长方形的 。
8.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.
9.如果一个平行四边形和一个长方形的周长相等,那么面积也一定相等。
三、填空题
10.有一个三角形,底长1.25米,高是0.8米,这个三角形的面积是________平方米
11.平行四边形的面积:________cm2
12.下图平行四边形的面积是15cm2 , 阴影部分的面积是________.
13.如图,已知阴影的面积为24平方厘米,那么大梯形的面积是________平方厘米。
14.一个梯形的面积是75 cm2 , 上底是5 cm,高是10 cm,它的下底是 ________?cm。
四、计算题
15.求下面图形的周长和面积.(单位:米)
五、解答题
16.图中每个小方格的面积是1cm2 , 请估计这个图形的面积。
17.计算下面图形的面积。
六、综合题
18.根据要求回答问题:
(1)在下面的梯形中画出一个最大的三角形.
(2)量出这个三角形的相关数据(取整厘米) 算出它的面积.
七、应用题
19.如图,在平行四边形ABCD中,AE= AB,BF= BC.AF与CE相交于O点,已知BC的长是16厘米,BC边上的高是9厘米,那么四边形AOCD的面积是多少平方厘米?
20.如图三角形ABC是直角三角形,边AB长12厘米,BC长4厘米,求阴影部分面积
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】3.5×6=21(平方米)
故答案为:D
【分析】底是3.5m,高是6m,根据“平行四边形面积=底×高”列式计算面积.
2.【答案】 C
【解析】【解答】解:6÷ =12(厘米).
答:三角形的高是12厘米.
故选:C.
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,由“一个三角形和一个平行四边形的底相等,面积也相等”可知,平行四边形的高是三角形的高的 ,从而问题得解.
3.【答案】C
【解析】【解答】解:10×8=80(平方厘米);
答:这个平行四边形的面积是80平方厘米.
故选:C.
【分析】依据在直角三角形中斜边最长,先判断出10厘米高的对应底边是8厘米,进而利用平行四边形的面积公式即可求解.解答此题的关键是:先确定出已知高的对应底边,即可求其面积.
4.【答案】B
【解析】【解答】因为梯形的面积=(上底+下底)×高÷2,“上底增加3厘米,下底减少3厘米,面积不变”则(上底+下底)的和不变,且面积不变,所以梯形的高不变。
故选:B
【分析】梯形的面积=(上底+下底)×高÷2,若“上底增加3米,下底减少3米,面积不变”则(上底+下底)的和不变,且面积不变,从而得知梯形的高也不变。
5.【答案】 B
【解析】【解答】三角形的面积为:面积=底×高÷2
则:同底等高的两个三角形的面积一定相等。
【分析】根据三角形的面积公式=底×高÷2,可知三角形面积的大小是由它的底和高决定的,所以同底等高的两个三角形的面积一定相等。掌握同底等高的两个三角形的面积相等。
二、判断题
6.【答案】错误
【解析】【解答】面积相同的两个梯形,形状可能相同,可能不同,原题说法错误.
故答案为:错误.
【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此判断.
7.【答案】正确
【解析】【解答】解:(2×2÷2×2)÷(2×8)
=4÷16
=
原题计算正确.
故答案为:正确
【分析】两块阴影部分是等底等高的三角形,根据面积公式分别计算阴影部分的面积之和和长方形的面积,用阴影部分面积除以长方形面积即可.
8.【答案】正确
【解析】【解答】解:拿走一个小方块,大正方体的表面看似少了三个面,其实又多出来三个面,所以它的表面积是不变的.
故答案为:正确.
【分析】由题意知,拼成的正方体长、宽、高应该都是2厘米,即上下各4个小方块,且每个小方块都处在一个角上,每个小方块都有三个面组成大正方体的表面,拿走一个,就少三个面,但又多了三个面,从而题目得解.此题主要考查正方体的表面积,关键是弄清楚少了三个面,又多了三个面.
9.【答案】错误
【解析】【解答】解:如果一个平行四边形和一个长方形的周长相等,但面积不一定相等。
故答案为:错误。
【分析】平行四边形的周长=(底+腰)×2,长方形的周长=(长+宽)×2,如果一个平行四边形和一个长方形的周长相等,即平行四边形的底+腰=长方形的长+宽,它们之间只存在一个等量关系,并不要求对应相等,而平行四边形的面积=底×高,长方形的面积=长×宽,所以它们的面积不一定相等。
三、填空题
10.【答案】0.5
【解析】【解答】解:1.25×0.8÷2=0.5(平方米)
故答案为:0.5平方米
【分析】本题考查的主要内容是三角形的面积计算问题,根据三角形的面积=底×高÷2进行分析即可.
11.【答案】72
【解析】【解答】解:8×9=72(平方厘米)
故答案为:72.
【分析】本题考查的主要内容是平行四边形的面积的应用问题,根据平行四边形的面积公式进行分析即可.
12.【答案】7.5平方厘米
【解析】【解答】解:15÷2=7.5(平方厘米)则阴影部分的面积是7.5平方厘米.
故答案为:7.5平方厘米.
【分析】阴影部分的三角形与平行四边形等底等高,所以三角形面积是平行四边形面积的一半,由此用平行四边形面积除以2就是阴影部分的面积.
13.【答案】38
【解析】【解答】解:24×2÷12=4(厘米),梯形面积:
(7+12)×4÷2
=19×4÷2
=38(平方厘米)。
故答案为:38。
【分析】用阴影部分三角形面积的2倍除以底即可求出高,梯形的高与三角形的高相等,再根据梯形面积公式计算大梯形面积即可。
14.【答案】10
【解析】【解答】75×2÷10-5
=150÷10-5
=15-5
=10(cm)
故答案为:10.【分析】已知梯形的面积及上底和高,求梯形的下底,用梯形的面积×2÷高-上底=下底,据此列式解答.
四、计算题
15.【答案】解:周长:2.5×2+2+3.14×2÷2,
=5+2+3.14,
=10.14(米),
面积:2.5×2+3.14× ÷2,
=5+3.14×1÷2,
=5+1.57,
=6.57(平方米),
答:这个图形的周长是10.14米,面积是6.57平方米
【解析】【分析】(1)要求它的周长,可用长方形的2个长+一个宽+圆的周长的一半;(2)要求它的面积,可用图中长方形的面积加上半圆的面积即可.组合图形的计算,一般都要把它转移到规则图形中进行计算.
五、解答题
16.【答案】解:6×8=48(cm2)(答案不唯一)
答:估计这个图形的面积是48平方厘米。
【解析】【分析】可以把它看作一个近似的平行四边形来计算面积,底是8cm,高是6cm,用底乘高求出面积即可。
17.【答案】解:(16-9)×(10-4.5)÷2+16×4.5
=7×5.5÷2+72
=19.25+72
=91.25(平方米)
答:图形的面积是91.25平方米.
【解析】【分析】根据题意可知,组合图形可以分成一个三角形和一个长方形,三角形的底是10-4.5=5.5米,三角形的高是16-9=7米,然后用三角形的面积+长方形的面积=组合图形的面积,据此列式解答.
六、综合题
18.【答案】 (1)如图所示:
(2)解:测量可得:三角形底4厘米,高3厘米,
4×3÷2=6(平方厘米)
答:它的面积是6平方厘米.
【解析】【分析】(1)梯形中面积最大的三角形是以梯形较长底边为底,与梯形等高的三角形;(2)先量出三角形的底和高,再根据三角形的面积公式:三角形面积=底×高÷2计算即可.解答此题的关键是明确梯形中面积最大的三角形是指哪一部分.
七、应用题
19.【答案】解:因为BF= BC=3FC,所以S△ABF=3S△AFC,S△BOF=3△FOC,故S△ABO=3S△AOC;
又AE= AB=2BE,所以SABO= △S△AOE,S△AEC= S△ABC,
故S△AOC= S△AOE= S△AEC= S△ABC.
而S△ABC=S△ACD= SABCD= ×16×9=72(平方厘米),
因此四边形AOCD的面积=S△AOC+S△ACD= ×72+72=16+72=88(平方厘米).
答:四边形AOCD的面积是88平方厘米.
【解析】【分析】要求四边形AOCD的面积,只要求出三角形AOC和ACD的面积即可,可以通过作辅助线加以解答.如图,连接AC和OB.此题设计较精彩,融合了三角形、四边形与多边形的面积与一体,重在考查学生对平面图形面积计算的分析与掌握情况.
20.【答案】解:设半圆的半径为x厘米,则
(12﹣x):12=x:4
????????? 12x=4(12﹣x)
????????? 12x=48﹣4x
????????? 16x=48
??? 16x÷16=48÷16
???????????? x=3
12×4÷2﹣3.14×32÷2
=24﹣3.14×9÷2
=24﹣14.13
=9.87(平方厘米)
答:阴影部分面积是9.87平方厘米
【解析】【分析】首先根据相似三角形的性质得到半圆的半径,再根据阴影部分面积=三角形的面积﹣半圆的面积,代入数据计算即可求解.考查了组合图形的面积,本题关键是理解阴影部分面积=三角形的面积﹣半圆的面积,难点是得到半圆的半径.
