19.3 正方形(试卷)
图片预览


文档简介
19.3 正方形
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.正方形具有而菱形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.四条边相等
2.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是( )
A.AO=CD B.AO=CO=BO=DO
C.AO=CO,BO=DO,AC⊥BD D.AO=BO=CO=DO,AC⊥BD
3. 甲、乙、丙、丁四位同学到工厂实习,工人师傅拿一把尺子要他们帮助检测一个四边形构件是否为正方形,他们各自做了如下检测:
甲量得构件四边都相等;乙量得构件的两条对角线相等;丙量得构件的一组邻边相等;丁量得构件的四边相等且两条对角线也相等.检测后,他们都说是正方形,你认为说得最有把握的是( )
A.甲 B.乙 C.丙 D.丁
4. 如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.如图,延长正方形ABCD的一边BC至E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( )
A.112.5° B.120° C.122.5° D.135°
6.如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2016次相遇在边( )
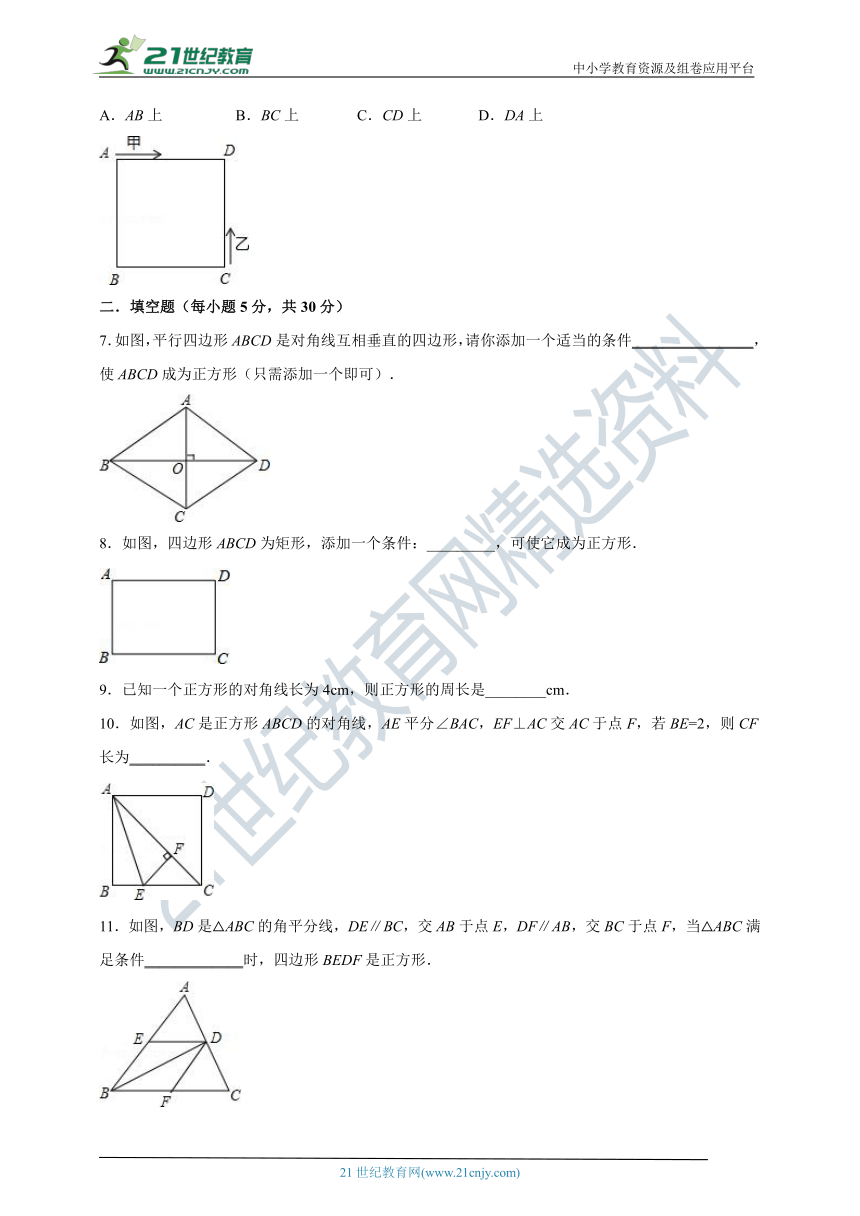
A.AB上 B.BC上 C.CD上 D.DA上
二.填空题(每小题5分,共30分)
7.如图,平行四边形ABCD是对角线互相垂直的四边形,请你添加一个适当的条件________________,使ABCD成为正方形(只需添加一个即可).
8.如图,四边形ABCD为矩形,添加一个条件:_________,可使它成为正方形.
9.已知一个正方形的对角线长为4cm,则正方形的周长是________cm.
10.如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为__________.
11.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件_____________时,四边形BEDF是正方形.
12.如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF=_________.
三、解答题(共40分)
13.(本题满分12分)如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
14.(本题满分14分)如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.
求证:四边形DECF是正方形.
15.(本题满分14分)如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
参考答案
一、选择题:
1.【答案】A.
【解析】正方形的性质有:四条边都相等,四个角都是直角,对角线互相平分垂直且相等,而且平分一组对角;菱形的性质有:四条边都相等,对角线互相垂直平分.∴正方形具有而菱形不一定具有的性质是:对角线相等.故选A.
2.【答案】D.
【解析】A、不能判定为特殊的四边形;B、只能判定为矩形;C、只能判定为菱形;D、能判定为正方形;故选D.
3.【答案】D.
【解析】甲:∵构件四边都相等,∴此四边形是菱形;
乙:∵两条对角线相等,∴没法判定是什么四边形;
丙:∵一组邻边相等,∴没法判定是什么四边形;
丁:∵四边相等,∴此四边形是菱形,∵两条对角线也相等,∴此四边形是正方形.故选D.
4.【答案】D.
【解析】由正方形的性质知,①②③都正确,故选D.
5.【答案】A.
【解析】AC是正方形的对角线,∴∠ACD=∠ACB=45°,∴∠ACE=∠ACD+∠DCE=135°,又∵CE=AC,∴∠CEF=22.5°,∴∠AFC=90°+22.5°=112.5°.故选A.
6.【答案】D.
【解析】根据题意分析可得:乙的速度是甲的速度的4倍,故第1次相遇,甲走了正方形周长的;从第2次相遇起,每次甲走了正方形周长的,从第3次相遇起,5次一个循环.因此可得:从开始出发起,每次相遇的位置依次是:AD,DC,点C,CB,BA;依次循环.故它们第2016次相遇位置在边DA上.故选D.
二、填空题:
7.【答案】∠ABC=90°.
【解析】添加条件:∠ABC=90°;理由如下:∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,∵∠ABC=90°,∴四边形ABCD是正方形.
8.【答案】AB=AD.
【解析】∵四边形ABCD是矩形,∴当AB=AD或AC⊥BD时,矩形ABCD是正方形.故答案为:AB=AD.
9.【答案】8.
【解析】边长是4×=2cm.则周长是:8cm.
10.【答案】2.
【解析】∵四边形ABCD是正方形,∴∠B=90°,∠ACB=∠DCB=45°,∵AE平分∠BAC,EF⊥AC,∴BE=EF,∵EF⊥AC,∴∠EFC=90°,∵∠ACB=45°,∴∠FEC=45°=∠FCE,∴EF=FC=BE=2.
11.【答案】∠ABC=90°.
【解析】当△ABC满足条件∠ABC=90°,四边形DEBF是正方形.理由:∵DE∥BC,DF∥AB,∴四边形DEBF是平行四边形∵BD是∠ABC的平分线,∴∠EBD=∠FBD,又∵DE∥BC,∴∠FBD=∠EDB,则∠EBD=∠EDB,∴BE=DE.故平行四边形DEBF是菱形,当∠ABC=90°时,菱形DEBF是正方形.故答案为:∠ABC=90°.
12.【答案】2.
【解析】∵∠FDC+∠DCF=90°,∠CDF+∠ADE=90°,∴∠FDC=∠ADE,∵AE⊥DP于E点,CF⊥DP于F点∴∠CFD=∠AED=90°,∵CD=AD,在△CBF和△BAE中,∵,∴△CDF≌△DAE(AAS).∴DE=CF=5,DF=AE=3,∴EF=DE﹣DF=5﹣3=2.
三、解答题:
13.【答案】见解析.
【解析】证明:∵四边形ABCD是正方形,∴AD=CD,∠EAD=∠BCD=90°,∴∠FCD=90°,在△ADE和△CDF中,∵,∴△ADE≌△CDF(SAS),∴DE=DF.
14.【答案】见解析.
【解析】证明:∵CD是角平分线,DE⊥AC,DF⊥BC,∴DE=DF,∠CED=∠CFD=90°,∵∠ACB=90°,∴四边形DECF是矩形,又∵DE=DF,∴四边形DECF是正方形.
15.【答案】(1)见解析;(2)115°.
【解析】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∵AE⊥l于点E,∴∠ABE+∠BAE=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,∵,∴△ABE≌△BCF(AAS);
(2)∵△ABE≌△BCF,∠CBF=65°,∴∠BAE=65°,又由正方形ABCD得AB∥DC,∴∠AGD=∠BAE=65°,∴∠AGC=115°.
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.正方形具有而菱形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.四条边相等
2.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是( )
A.AO=CD B.AO=CO=BO=DO
C.AO=CO,BO=DO,AC⊥BD D.AO=BO=CO=DO,AC⊥BD
3. 甲、乙、丙、丁四位同学到工厂实习,工人师傅拿一把尺子要他们帮助检测一个四边形构件是否为正方形,他们各自做了如下检测:
甲量得构件四边都相等;乙量得构件的两条对角线相等;丙量得构件的一组邻边相等;丁量得构件的四边相等且两条对角线也相等.检测后,他们都说是正方形,你认为说得最有把握的是( )
A.甲 B.乙 C.丙 D.丁
4. 如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.如图,延长正方形ABCD的一边BC至E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( )
A.112.5° B.120° C.122.5° D.135°
6.如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2016次相遇在边( )
A.AB上 B.BC上 C.CD上 D.DA上
二.填空题(每小题5分,共30分)
7.如图,平行四边形ABCD是对角线互相垂直的四边形,请你添加一个适当的条件________________,使ABCD成为正方形(只需添加一个即可).
8.如图,四边形ABCD为矩形,添加一个条件:_________,可使它成为正方形.
9.已知一个正方形的对角线长为4cm,则正方形的周长是________cm.
10.如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为__________.
11.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件_____________时,四边形BEDF是正方形.
12.如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF=_________.
三、解答题(共40分)
13.(本题满分12分)如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
14.(本题满分14分)如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.
求证:四边形DECF是正方形.
15.(本题满分14分)如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
参考答案
一、选择题:
1.【答案】A.
【解析】正方形的性质有:四条边都相等,四个角都是直角,对角线互相平分垂直且相等,而且平分一组对角;菱形的性质有:四条边都相等,对角线互相垂直平分.∴正方形具有而菱形不一定具有的性质是:对角线相等.故选A.
2.【答案】D.
【解析】A、不能判定为特殊的四边形;B、只能判定为矩形;C、只能判定为菱形;D、能判定为正方形;故选D.
3.【答案】D.
【解析】甲:∵构件四边都相等,∴此四边形是菱形;
乙:∵两条对角线相等,∴没法判定是什么四边形;
丙:∵一组邻边相等,∴没法判定是什么四边形;
丁:∵四边相等,∴此四边形是菱形,∵两条对角线也相等,∴此四边形是正方形.故选D.
4.【答案】D.
【解析】由正方形的性质知,①②③都正确,故选D.
5.【答案】A.
【解析】AC是正方形的对角线,∴∠ACD=∠ACB=45°,∴∠ACE=∠ACD+∠DCE=135°,又∵CE=AC,∴∠CEF=22.5°,∴∠AFC=90°+22.5°=112.5°.故选A.
6.【答案】D.
【解析】根据题意分析可得:乙的速度是甲的速度的4倍,故第1次相遇,甲走了正方形周长的;从第2次相遇起,每次甲走了正方形周长的,从第3次相遇起,5次一个循环.因此可得:从开始出发起,每次相遇的位置依次是:AD,DC,点C,CB,BA;依次循环.故它们第2016次相遇位置在边DA上.故选D.
二、填空题:
7.【答案】∠ABC=90°.
【解析】添加条件:∠ABC=90°;理由如下:∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,∵∠ABC=90°,∴四边形ABCD是正方形.
8.【答案】AB=AD.
【解析】∵四边形ABCD是矩形,∴当AB=AD或AC⊥BD时,矩形ABCD是正方形.故答案为:AB=AD.
9.【答案】8.
【解析】边长是4×=2cm.则周长是:8cm.
10.【答案】2.
【解析】∵四边形ABCD是正方形,∴∠B=90°,∠ACB=∠DCB=45°,∵AE平分∠BAC,EF⊥AC,∴BE=EF,∵EF⊥AC,∴∠EFC=90°,∵∠ACB=45°,∴∠FEC=45°=∠FCE,∴EF=FC=BE=2.
11.【答案】∠ABC=90°.
【解析】当△ABC满足条件∠ABC=90°,四边形DEBF是正方形.理由:∵DE∥BC,DF∥AB,∴四边形DEBF是平行四边形∵BD是∠ABC的平分线,∴∠EBD=∠FBD,又∵DE∥BC,∴∠FBD=∠EDB,则∠EBD=∠EDB,∴BE=DE.故平行四边形DEBF是菱形,当∠ABC=90°时,菱形DEBF是正方形.故答案为:∠ABC=90°.
12.【答案】2.
【解析】∵∠FDC+∠DCF=90°,∠CDF+∠ADE=90°,∴∠FDC=∠ADE,∵AE⊥DP于E点,CF⊥DP于F点∴∠CFD=∠AED=90°,∵CD=AD,在△CBF和△BAE中,∵,∴△CDF≌△DAE(AAS).∴DE=CF=5,DF=AE=3,∴EF=DE﹣DF=5﹣3=2.
三、解答题:
13.【答案】见解析.
【解析】证明:∵四边形ABCD是正方形,∴AD=CD,∠EAD=∠BCD=90°,∴∠FCD=90°,在△ADE和△CDF中,∵,∴△ADE≌△CDF(SAS),∴DE=DF.
14.【答案】见解析.
【解析】证明:∵CD是角平分线,DE⊥AC,DF⊥BC,∴DE=DF,∠CED=∠CFD=90°,∵∠ACB=90°,∴四边形DECF是矩形,又∵DE=DF,∴四边形DECF是正方形.
15.【答案】(1)见解析;(2)115°.
【解析】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∵AE⊥l于点E,∴∠ABE+∠BAE=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,∵,∴△ABE≌△BCF(AAS);
(2)∵△ABE≌△BCF,∠CBF=65°,∴∠BAE=65°,又由正方形ABCD得AB∥DC,∴∠AGD=∠BAE=65°,∴∠AGC=115°.
