高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件 新人教B版选修2_1(29张PPT)
文档属性
| 名称 | 高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件 新人教B版选修2_1(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-06 00:00:00 | ||
图片预览




文档简介
课件29张PPT。
2.3.1双曲线及其标准方程
椭圆:
3.引入问题: 若把椭圆中的距离“和”改为距离”差”那么动点的轨迹会发生怎样的变化呢
|MF1|+|MF2|=2a( 2a>2c>0)
若2a=2c,
若2a<2c,
平面内与两定点F1、F2的距离的和
等于常数2a(2a>|F1F2|>0)的点的轨迹. 点M的轨迹是椭圆
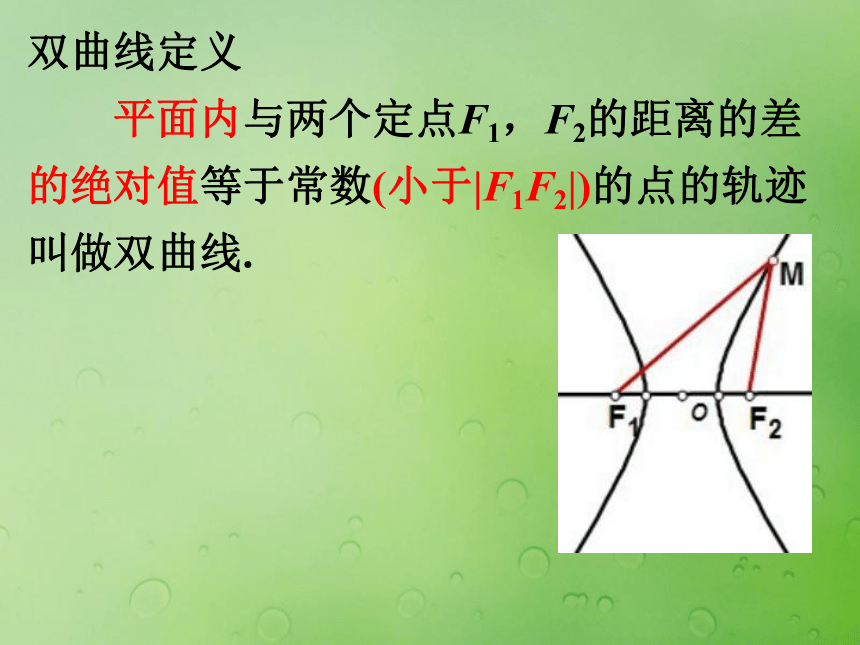
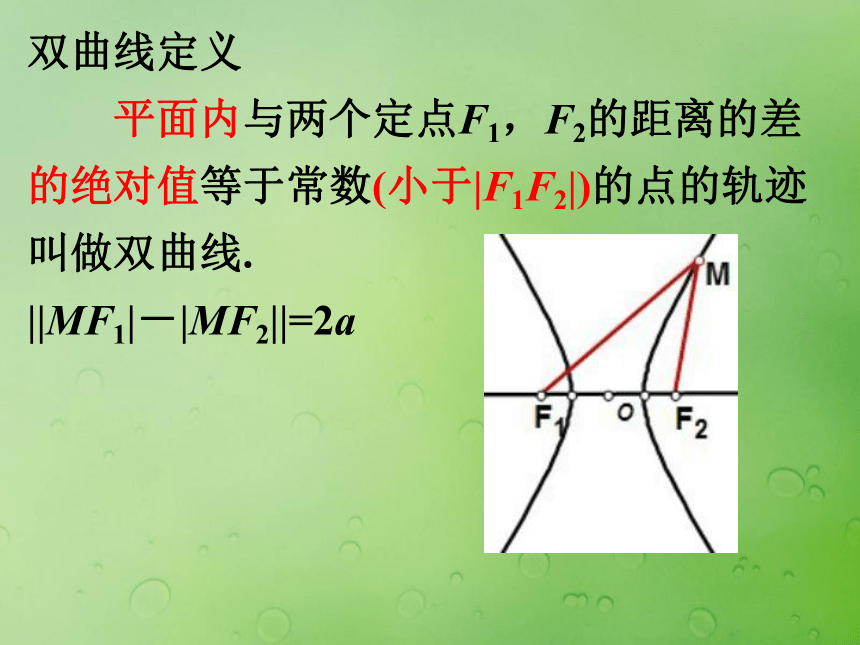
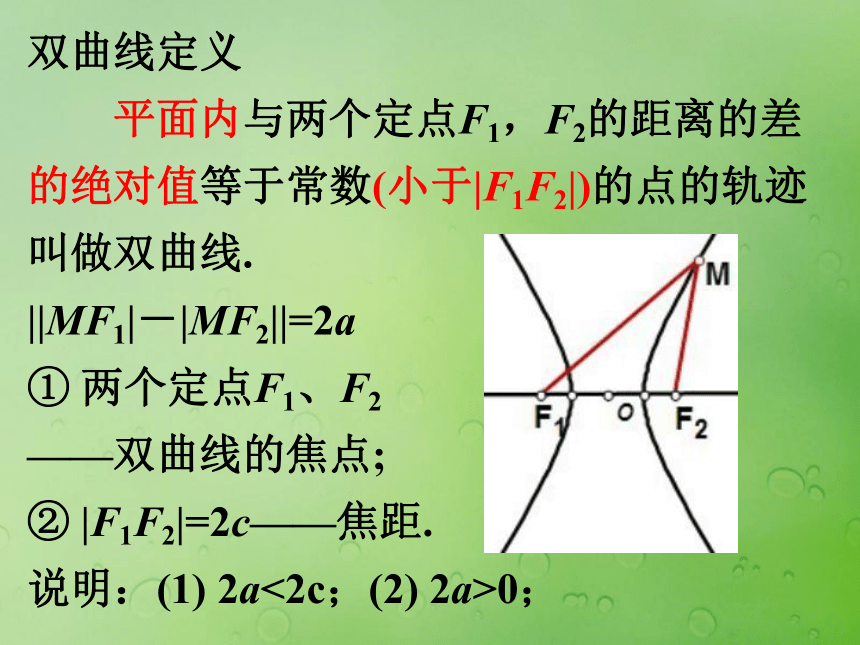
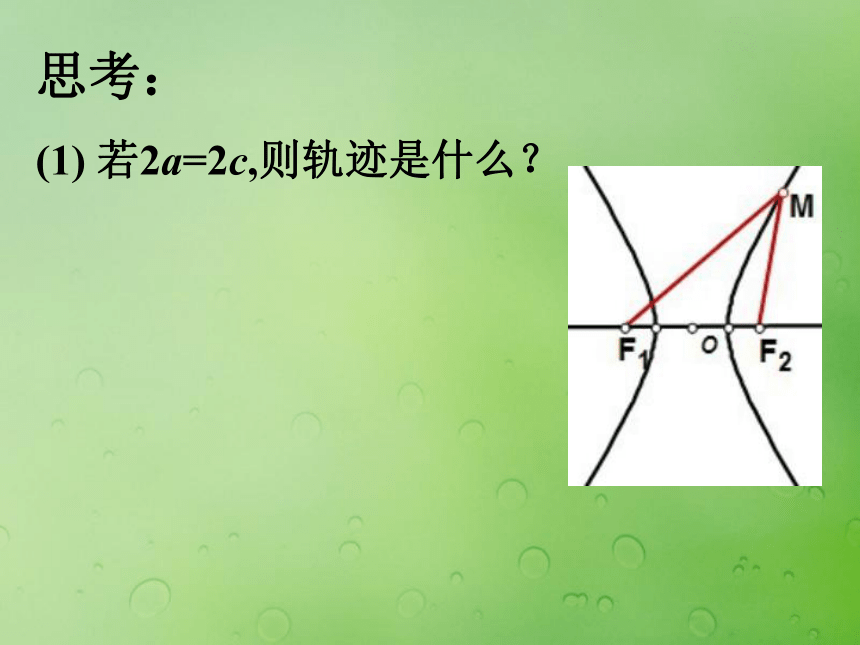
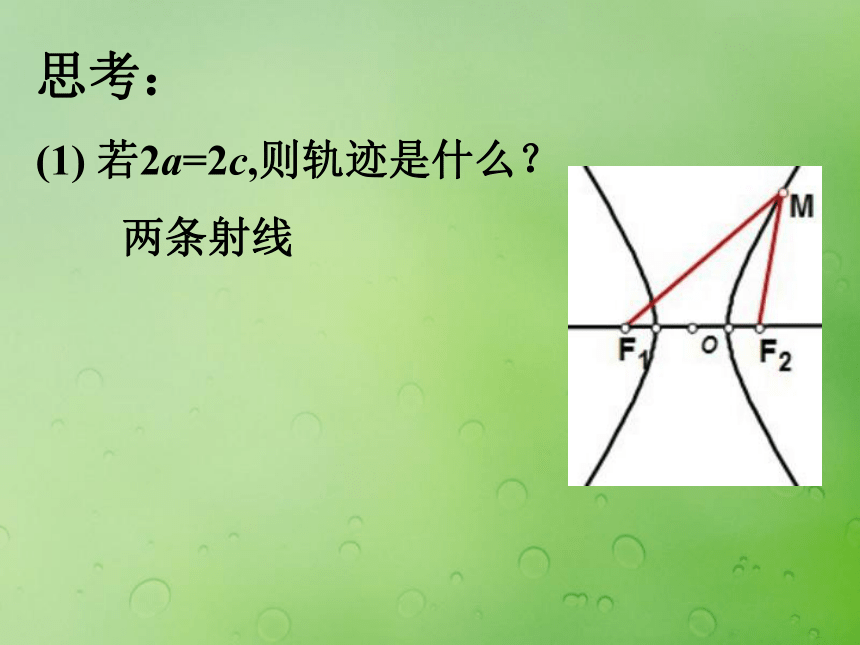
点M的轨迹是线段F1F2;点M的轨迹不存在。 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. ||MF1|-|MF2||=2a 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. ||MF1|-|MF2||=2a ① 两个定点F1、F2 ——双曲线的焦点; ② |F1F2|=2c——焦距. 说明:(1) 2a<2c;(2) 2a>0; ① |MF1|-|MF2|=|F2F|=2a ② |MF2|-|MF1|=|F1F|=2a 由①②可得: ||MF1|-|MF2||=2a (差的绝对值) 上面两条合起来叫做双曲线左支右支思考:由椭圆的定义,一般情况下,我们设该常数为2a,那么什么情况下表示双曲线的右支,什么情况下表示的是双曲线的左支?思考: (1) 若2a=2c,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹 (3) 若2a=0,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹 (3) 若2a=0,则轨迹是什么? 线段F1F2的垂直平分线双曲线的标准方程 双曲线的标准方程 1. 建系. 以F1,F2所在的直线 为x轴,线段F1F2的中点 为原点建立直角坐标系 2. 设点. 设M(x,y),则F1(-c,0),F2(c,0) 3. 列式.|MF1|-|MF2|=?2axy双曲线的标准方程 1. 建系. 以F1,F2所在的直线 为x轴,线段F1F2的中点 为原点建立直角坐标系 2. 设点. 设M(x,y),则F1(-c,0),F2(c,0) 3. 列式.|MF1|-|MF2|=?2a4. 化简xyF1M类比椭圆的标准方程你能否得到焦点在y 轴上的方程?***问题*** 1. 如何判断双曲线的焦点在哪个轴上?***问题*** 1. 如何判断双曲线的焦点在哪个轴上? 2. 双曲线的标准方程与椭圆的标准方程有何区别与联系? [例1] 已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2||=6,求动点P的轨迹方程. 变式训练1:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2|| =10,求动点P的轨迹方程. 变式训练1:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2|| =10,求动点P的轨迹方程. 变式训练2:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:|PF1|-|PF2| =6,求动点P的轨迹方程. [例2] 如果方程 表示双曲线,求m的取值范围. [例2] 如果方程 表示双曲线,求m的取值范围.思考: 方程 表示焦点在y轴双曲线时,则m的取值范围__________. [例2] 如果方程 表示双曲线,求m的取值范围.思考: 方程 表示焦点在y轴双曲线时,则m的取值范围__________.m<-2 [例3] 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.xyABP [例3] 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.***学习小结***
本节课主要是进一步了解双曲线的定义及其标准方程,并运用双曲线的定义及其标准方程解决问题.
2.3.1双曲线及其标准方程
椭圆:
3.引入问题: 若把椭圆中的距离“和”改为距离”差”那么动点的轨迹会发生怎样的变化呢
|MF1|+|MF2|=2a( 2a>2c>0)
若2a=2c,
若2a<2c,
平面内与两定点F1、F2的距离的和
等于常数2a(2a>|F1F2|>0)的点的轨迹. 点M的轨迹是椭圆
点M的轨迹是线段F1F2;点M的轨迹不存在。 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. ||MF1|-|MF2||=2a 双曲线定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线. ||MF1|-|MF2||=2a ① 两个定点F1、F2 ——双曲线的焦点; ② |F1F2|=2c——焦距. 说明:(1) 2a<2c;(2) 2a>0; ① |MF1|-|MF2|=|F2F|=2a ② |MF2|-|MF1|=|F1F|=2a 由①②可得: ||MF1|-|MF2||=2a (差的绝对值) 上面两条合起来叫做双曲线左支右支思考:由椭圆的定义,一般情况下,我们设该常数为2a,那么什么情况下表示双曲线的右支,什么情况下表示的是双曲线的左支?思考: (1) 若2a=2c,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹 (3) 若2a=0,则轨迹是什么?思考: (1) 若2a=2c,则轨迹是什么? 两条射线 (2) 若2a>2c,则轨迹是什么? 不表示任何轨迹 (3) 若2a=0,则轨迹是什么? 线段F1F2的垂直平分线双曲线的标准方程 双曲线的标准方程 1. 建系. 以F1,F2所在的直线 为x轴,线段F1F2的中点 为原点建立直角坐标系 2. 设点. 设M(x,y),则F1(-c,0),F2(c,0) 3. 列式.|MF1|-|MF2|=?2axy双曲线的标准方程 1. 建系. 以F1,F2所在的直线 为x轴,线段F1F2的中点 为原点建立直角坐标系 2. 设点. 设M(x,y),则F1(-c,0),F2(c,0) 3. 列式.|MF1|-|MF2|=?2a4. 化简xyF1M类比椭圆的标准方程你能否得到焦点在y 轴上的方程?***问题*** 1. 如何判断双曲线的焦点在哪个轴上?***问题*** 1. 如何判断双曲线的焦点在哪个轴上? 2. 双曲线的标准方程与椭圆的标准方程有何区别与联系? [例1] 已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2||=6,求动点P的轨迹方程. 变式训练1:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2|| =10,求动点P的轨迹方程. 变式训练1:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:||PF1|-|PF2|| =10,求动点P的轨迹方程. 变式训练2:已知两定点F1(-5, 0)、F2(5, 0),动点P满足:|PF1|-|PF2| =6,求动点P的轨迹方程. [例2] 如果方程 表示双曲线,求m的取值范围. [例2] 如果方程 表示双曲线,求m的取值范围.思考: 方程 表示焦点在y轴双曲线时,则m的取值范围__________. [例2] 如果方程 表示双曲线,求m的取值范围.思考: 方程 表示焦点在y轴双曲线时,则m的取值范围__________.m<-2 [例3] 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.xyABP [例3] 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.***学习小结***
本节课主要是进一步了解双曲线的定义及其标准方程,并运用双曲线的定义及其标准方程解决问题.
