3.2 图形的旋转（1）-试卷

3.2 图形的旋转（1）
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题8分）
1．下列现象是数学中的平移的是（ ）
A．小朋友荡秋千 B．碟片在光驱中运行
C．“神舟”十号宇宙飞船绕地球运动 D．瓶装饮料在传送带上移动
2．4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180°后得到如图（2）所示，那么她所旋转的牌从左起是（ ）
/
A．第一张 B．第二张 C．第三张 D．第四张
3．如图，将????△??????绕直角顶点C顺时针旋转
90
°
，得到△??′??′??，连接????′，若∠1=
25
°
，则∠??????′的度数是（ ）
A．
55
°
B．
60
°
C．
65
°
D．
70
°
/ / /
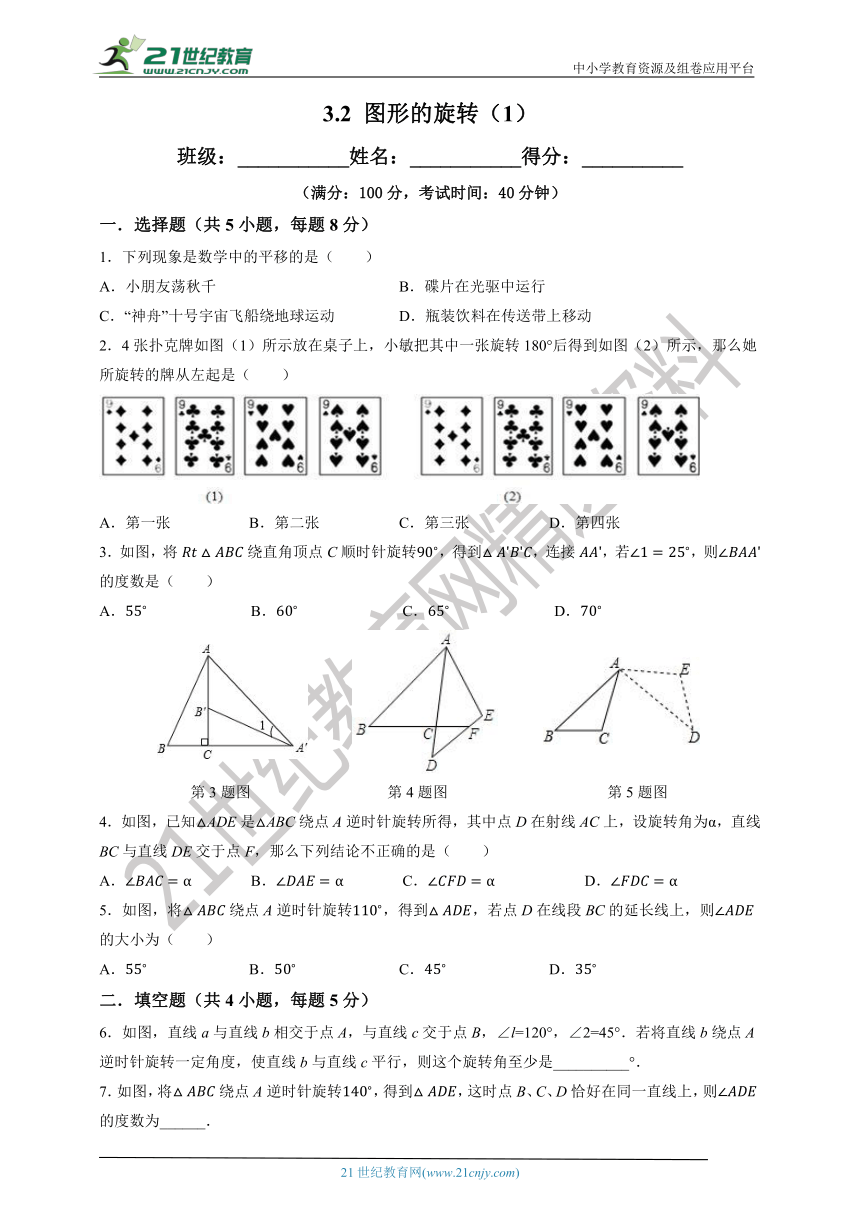
第3题图 第4题图 第5题图
4．如图，已知△ADE是△ABC绕点A逆时针旋转所得，其中点D在射线AC上，设旋转角为α，直线BC与直线DE交于点F，那么下列结论不正确的是（ ）
A．∠??????=α B．∠??????=α C．∠??????=α D．∠??????=α
5．如图，将△??????绕点A逆时针旋转
110
°
，得到△??????，若点D在线段BC的延长线上，则∠??????的大小为（ ）
A．
55
°
B．
50
°
C．
45
°
D．
35
°
二．填空题（共4小题，每题5分）
6．如图，直线a与直线b相交于点A，与直线c交于点B，∠l=120°，∠2=45°．若将直线b绕点A逆时针旋转一定角度，使直线b与直线c平行，则这个旋转角至少是__________°．
7．如图，将△??????绕点A逆时针旋转
140
°
，得到△??????，这时点B、C、D恰好在同一直线上，则∠??????的度数为______．
8．如图，将△??????绕点O按逆时针方向旋转
45
°
后得到△??′????′，若∠??????=
15
°
，则∠??????′的度数是______．
9．如图，点P为等边△ABC内一点，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP＝2，那么PP′＝_____．
/ / / /
第6题图 第7题图 第8题图 第9题图
三．解答题（共3小题，第10题10分，第11、12题各15分）
10．已知：如图，在△??????中，∠??????=
90
°
，将△??????绕点B按逆时针方向旋转
53
°
得到△??????，点C在边BD上．求：∠??的度数．
/
11．如图所示，∠DBC＝90°，∠C＝45°，AC＝2，△ABC绕点B逆时针旋转60°得到△DBE，连接AE．
（1）求证：△ABC≌△ABE；
（2）连接AD，求AD的长．
/
12．如图1，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°.
（1）将图1中的三角板OMN绕点O按逆时针方向旋转，使∠BON=30°，如图2，MN与CD相交于点E，求∠CEN的度数；
（2）将图1中的三角尺OMN绕点O按每秒20°的速度沿逆时针方向旋转一周，在旋转的过程中，求在第几秒时，边MN恰好与边CD平行？（友情提醒：先画出符合题意的图形，然后再探究）
/
试题解析
1．D
【解析】根据平移的定义，结合选项一一分析，排除错误答案．
解：A. 小朋友荡秋千是旋转，故选项A错误；
B. 碟片在光驱中运行是旋转，故选项B错误；
C. “神舟”十号宇宙飞船绕地球运动不是沿直线运动，故选项C错误．
D. 瓶装饮料在传送带上移动沿直线运动，符合平移定义，故选项D正确；
故选：D．
2．A
【解析】当所有图形都没有变化的时候，旋转的是成中心对称图形的，有变化的时候，旋转的便是有变化的．
解：观察两个图中可以发现，所有图形都没有变化，所以旋转的扑克是成中心对称的第一张．故选：A．
3．C
【解析】根据旋转的性质可得????=??′??，可判断出△??????′是等腰直角三角形，根据等腰直角三角形的性质可得∠??????′=
45
°
，再计算角的和差即可得出答案．
解：∵????△??????绕直角顶点C顺时针旋转
90
°
得到△??′??′??，
∴????=??′??，∠??????=∠????′??′，
∴△??????′是等腰直角三角形，
∴∠????′??=
45
°
，
∵∠1=
25
°
，
∴∠??????=∠
????
′
??
′
=
20
°
，
∴∠
??????
′
=
20
°
+
45
°
=
65
°
.
故选：C．
4．D
【解析】利用旋转不变性即可解决问题．
解：∵△DAE是由△BAC旋转得到，∴∠BAC=∠DAE=α，∠B=∠D，∵∠ACB=∠DCF，∴∠CFD=∠BAC=α，故A，B，C正确，故选：D．
5．D
【解析】根据旋转的性质可得????=????，∠??????=
110
°
，∠??????=∠??????，根据等腰三角形的性质可得∠??????=∠??????=
35
°
．
解：如图，连接CD，
/
∵将△??????绕点A逆时针旋转
110
°
，得到△??????，
∴????=????，∠??????=
110
°
，∠??????=∠??????，
∴∠ABC=∠ADB=（180°-∠BAD）÷2=35°，
∴∠ADE=∠??????=
35
°
，
故选D．
6．15
【解析】根据平行线的性质可得旋转角的度数.
解：∵∠1＝120°，
∴∠3＝60°，
∵∠2＝45°，
∴当∠3＝∠2＝45°时，b∥c，
∴直线b绕点A逆时针旋转60°﹣45°＝15°，即这个旋转角至少是15°．
故答案为：15．
7．
20
°
【解析】根据旋转性质可知∠??????=∠??，∠??????=
140
°
，且????=????，在等腰三角形BAD中求∠??度数即可．
解：根据旋转的性质可知∠??????=∠??，????=????，∠??????=
140
°
，
∵点B、C、D恰好在同一直线上，
∴∠??=∠??????=∠??????=
1
2
(
180
°
?
140
°
)=
20
°
．
故答案为
20
°
．
8．
30
°
【解析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角，进而得出答案即可．
解：∵将△??????绕点O按逆时针方向旋转
45
°
后得到△??′????′，
∴∠??′????=
45
°
，∠??????=∠??′????′=
15
°
，
∴∠??????′=∠??′?????∠??′????=
45
°
?
15
°
=
30
°
，
故答案是：
30
°
．
9．2
【解析】根据等边三角形的性质得出∠BAC＝60°，根据旋转的性质得出AP＝AP′，∠BAC＝∠PAP′＝60°，根据等边三角形的判定得出△APP′是等边三角形，根据等边三角形的性质得出即可．
解：∵△ABC是等边三角形，
∴AB＝AC，∠BAC＝60°，
∴旋转角的度数为60°，
即∠PAP′＝∠BAC＝60°，
根据旋转得出AP＝AP′，
∴△APP′是等边三角形，
∴PP′＝AP，
∵AP＝2，
∴PP′＝2，
故答案为：2．
10．详见解析.
【解析】根据旋转的性质可知△??????≌△??????，得到∠??=
90
°
，旋转角∠??????=
53
°
，在△??????中利用三角形内角和
180
°
求解∠??度数即可．
解：根据旋转的性质可知△??????≌△??????，
∴∠??=∠??????=
90
°
．
又∠??????=
53
°
，
∴∠??=
90
°
?
53
°
=
37
°
．
11．（1）见解析；（2）2
2
.
【解析】（1）根据旋转的性质得到∠DBE＝∠ABC，∠EBC＝60°，BE＝BC，根据全等三角形的判定定理即可得到结论；
（2）连接AD，根据旋转的性质得到DE＝AC，∠BED＝∠C，DE＝AC＝2，根据全等三角形的性质得到∠BEA＝∠C，AE＝AC＝2，根据等腰三角形的性质即可得到结论．
解：（1）证明：∵△ABC绕点B逆时针旋转60°得到△DBE，
∴∠DBE＝∠ABC，∠EBC＝60°，BE＝BC，
∵∠DBC＝90°，
∴∠DBE＝∠ABC＝30°，
∴∠ABE＝30°，
在△ABC与△ABE中，
????=????
∠??????=∠??????=30°
????=????
，
∴△ABC≌△ABE（SAS）；
（2）解：连接AD，
∵△ABC绕点B逆时针旋转60°得到△DBE，
∴DE＝AC，∠BED＝∠C，DE＝AC＝2，
∵△ABC≌△ABE，
∴∠BEA＝∠C，AE＝AC＝2，
∵∠C＝45°，
∴∠BED＝∠BEA＝∠C＝45°，
∴∠AED＝90°，DE＝AE，
∴AD＝
2
AE＝2
2
．
/
12．（ (1)∠CEN=135°；（2）3.75秒或12.75秒.
【解析】（1）根据内错角相等，两直线平行判断出MN∥BC，再根据两直线平行，同旁内角互补解答；
（2）作出图形，然后分两种情况求出旋转角，再根据时间=旋转角÷速度计算即可得解．
解：（1）∵∠BON=∠N=30°，
∴MN∥BC，
∴∠CEN=180°-∠DCO=180°-45°=135°；
（2）如图，MN∥CD时，旋转角为90°-（60°-45°）=75°，
或270°-（60°-45°）=255°，
所以，t=75°÷20°=3.75秒，
或225°÷20°=12.75秒
/
/